引言

暴雨内涝是城市频发的主要自然灾害类型。近年来，随着城市化进程的不断推进，天然植被逐渐被建筑和路面等人工下垫面所取代，导致对雨水的截留和下渗能力大大降低，地表径流迅速增大(朱冬冬等，2011)。研究表明，城市地区年平均洪水大小随地表不透水面积的增加而增大，一个完全城市化地区的年平均洪水径流量是相似天然流域的4~5倍(刘金平等，2009)，同时对于相同量级的暴雨，城市洪峰流量比天然流域高出几倍甚至数十倍(方增强，2001)。此外，城市的热岛效应又造成市区降水频率增大，强度增加(陈波和冯光柳，2008；陆敏等，2010)，可见在同等条件下城市更容易受到暴雨天气影响(Shi et al，2007)。加之城市区域人口密集、建筑集中、工商业和交通发达，因此城市遭遇内涝的损失也更加严重。

上海市位于长江入海口，区内地势低洼，属典型的平原感潮河口城市。近年来，上海多次遭受台风、暴雨的侵袭，甚至出现台风增水、区间暴雨和上游洪水“多碰头”的现象，造成了重大的财产损失。上海是中国经济发达的特大城市，其承灾体暴露度相对较高，面对严重的城市暴雨内涝灾害，基于城市内涝模型，开展精细化的暴雨内涝影响预报和风险预警是降低暴雨内涝灾害、减少财产损失的有效途径。

当前城市内涝分析模型大多基于水动力学方法构建(仇劲卫等，2000；李伟峰等，2009；张萍萍等，2010；Rossman，2010)，该方法通常需要详尽的管道数据用于搭建一维模型，然后将一维模型与二维地表漫流模型耦合，进行分析计算，但是目前多数城市都缺乏雨水系统的现状资料及详细的规划方案(尹志聪等，2015)，导致这种建模方式在实施中面临诸多的问题和挑战(马洪涛等，2014)。此外，水动力学模型往往只适用于较小的空间尺度，而不能满足对城市范围的模拟要求(陈晓燕等，2013)，这也给模型的推广应用带来了很大的困难。本研究以外环内中心城区为研究对象构建了上海暴雨内涝评估模型(Shanghai Urban Flooding Assessement Model, SUM)，通过对管道排水量进行概化处理，不仅解决了排水管网等数据的缺失导致无法搭建水力学模型的问题，更显著缩短了模型的运算时间，使得影响预报中模型的实时运算成为可能。此外，模型通过与短时临近降水格点化预报产品在预报时效上的对接，实现了对城市内涝1~24 h内逐小时的连续模拟，解决了当前概化模型只能模拟整个降雨过程的问题，为暴雨内涝的影响预报和风险评估提供了一定的技术支撑。

1 研究区域和资料 1.1 研究区概况

上海地处长江三角洲前缘，位于长江和太湖流域下游，东濒东海，南邻杭州湾，西接江苏、浙江两省，北界长江入海口，是长江三角洲冲积平原的一部分。上海市域地势低平，平均海拔仅4 m左右(上海吴淞高程)，区内河道水网密布，为典型的平原感潮河口城市。上海属于亚热带季风气候，四季分明，日照充足，雨量充沛，常年平均降雨量1259.4 mm，雨日128 d，一年中有50%的雨量都集中在6—9月的汛期(穆海振等，2015)。由于上海地处中纬度和海陆相过渡带且滨江临海，灾害性天气时有发生，几乎每年都不同程度地遭受台风(热带气旋)、暴雨、高潮和洪涝的侵袭，虽然城市河网密布，但受到排水设施老化、地势低洼和潮汐顶托等影响，城市排水能力较弱，暴雨内涝灾害频发(陆敏等，2010；尤凤春等，2013；郑传新等，2007)。

1.2 研究资料

研究资料包括上海市中心城区土地利用、水系、地表高程点、建筑楼层、排水区块等图层以及区内部分自动气象站及积水监测站数据。其中土地利用数据来源于上海市测绘部门提供的本市外环内12000土地利用矢量图，包括区内有林地、苗圃、停车场等37种土地利用类型。研究中结合水系图层对上述类别进行了重新划分，共定义出不透水区、透水区和水体三种类别，并重采样至5 m分辨率；中心城区地表高程利用区内147507个数字高程点构建5 m空间分辨率不规则三角网获得；建筑楼层和排水区块分别由上海市测绘及市政部门提供，为了便于模型计算，建筑楼层和排水区块数据同样重采样至5 m分辨率；区内自动站和积水监测数据则来源于上海市气象局。

2 研究方法

城市暴雨内涝是指降雨下落城市区域形成径流后由于地势低洼、排水不及时等原因造成的一定径流深度的地面积水(杨弋和吴升，2009)，而径流就其水体运动性质又可大致分为产流和汇流两个部分(杨辰等，2015)。研究基于SUM，分别针对产流和汇流两部分进行模拟计算，得到不同降雨情景下上海市中心城区的内涝积水深度、积水时间及受淹房屋分布等信息，为暴雨内涝的影响预报和风险预警提供一定的技术支撑。

2.1 城市地表产流模型

城市地表产流过程是指降雨量扣除损失形成净雨的过程，其中降雨损失包括植物截留、下渗、填洼和蒸散发等(任伯帜等，2006)，对于城市而言，产流作用以下渗为主。岑国平等(1997)研究表明，城市不透水区的比例对地表产流和径流滞时有较大影响，而随着不透水区比例的增加，径流系数也随之增大，因此本研究中将透水区和不透水区分开处理。由于暴雨通常历时短、强度高，在较高强度的暴雨期间基本无法蓄满便产流，所以透水区内的产流可采用Horton下渗曲线法进行模拟(张小娜，2007)。对于不透水面积，其降雨损失主要有洼蓄、植物截留和缝隙下渗等，研究表明，变径流系数法比较适用于不透水区的产流计算(岑国平等，1996)。综上所述，本研究分别采用Horton下渗曲线法和变径流系数法模拟城市透水区和不透水区的产流过程。

2.1.1 城市透水区产流计算

Horton下渗模型是由R. E. Horton于1933年提出的一个经验模型，它描述了土壤下渗能力由初始的最大值随时间通过指数形式衰减至一定的稳定入渗率(最小入渗率)的过程。该模型需要确定研究区域的最大入渗率、最小入渗率、入渗衰减系数等参数，其基本方程为：

$ {{f}_{t}}={{f}_{\infty }}+\left( {{f}_{0}}-{{f}_{\infty }} \right){{\rm{e}}^{\rm{-}\mathit{kt}}} $

(1)

式中，f_t为t时刻的下渗率(单位：mm·min^-1)；f₀和f_∞分别是初始下渗率和稳定下渗率(单位：mm·min^-1)；t为时间(单位：min)；k为下渗衰减系数(单位：min^-1)。

内涝模型中，需要计算累积下渗量，因此取上式的积分形式：

$ {{F}_{t}}=\int_{0}^{t}{{{f}_{t}}\rm{d}\mathit{t}}={{f}_{\infty }}t+\frac{{{f}_{0}}-{{f}_{\infty }}}{k}\left( \rm{1-}{{\rm{e}}^{\rm{-}\mathit{kt}}} \right) $

(2)

式中，F_t即为t时段内的累积下渗量(单位：mm)。本文根据研究区实际情况结合相关文献(张小娜，2007)，将初始下渗率、稳定下渗率以及下渗衰减系数分别取值2.8 mm·min^-1、0.2 mm·min^-1和0.04 min^-1。研究中，为了便于进行逐时段的内涝模拟，通常取前后2个时间段内的累积下渗量之差作为该时段的下渗量：

$ \left\{ \begin{align} &\Delta {{F}_{t}}={{F}_{t}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ t=1 \\ &\Delta {{F}_{t}}={{F}_{t+1}}-{{F}_{t}}\ \ \ t>1 \\ \end{align} \right. $

(3)

式中，ΔF_t为前后2个时段内的累积下渗量之差(单位：mm)，对于第一个时段而言，ΔF_t与F_t相等。

2.1.2 城市不透水区产流计算

在一场降雨中，降雨开始时洼蓄、下渗等损失量较大，径流系数较小，而随着降雨的持续，损失减小，径流系数增大，径流系数的变化可用下式表示：

$ \psi ={{\psi }_{\rm{e}}}-\left( {{\psi }_{\rm{e}}}-{{\psi }_{\rm{0}}} \right){{\rm{e}}^{\rm{-}\mathit{cP}}} $

(4)

式中，ψ为降雨过程中的径流系数，ψ_e为最终径流系数，ψ₀为初始径流系数，P为累积雨量，c为常数。由于相关参数值难以确定，因此依据武晟等(2006)对城市硬化地面径流系数随时间变化关系的试验研究结果计算不透水区产流，其最优拟合方程表示为：

$ \frac{1}{\psi }=1+\frac{a}{t-b} $

(5)

式中，t为时间(单位：min)；a、b为拟合系数，分别取值1.9和0.53(武晟等，2006)。在一场降雨过程中，径流系数是个变量，因此模型同样取上式的积分形式，可以得到t时段内的平均径流系数ψ_t：

$ {{\psi }_{t}}=\frac{\int_{0}^{t}{\psi \rm{d}\mathit{t}}}{t}=\frac{t-a\ln \left( t-b+a \right)}{t} $

(6)

由于产流量(R_t)可以直接通过径流系数(ψ_t)与降雨强度(i)求得，因此计算不透水区t时段内的平均产流量R_t为：

$ {{R}_{t}}=i{{\psi }_{t}} $

(7)

研究中，同样取前后2个时段内的产流量之差作为该时段的值：

$ \left\{ \begin{align} &\Delta {{R}_{t}}={{R}_{t}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ t=1 \\ &\Delta {{R}_{t}}={{R}_{t+1}}-{{R}_{t}}\ \ \ t>1 \\ \end{align} \right. $

(8)

式中，ΔR_t为前后2个时段内的产流量之差(单位：mm)，对于第一个时段而言，ΔR_t与R_t相等。

2.2 城市地表汇流模型

地表汇流过程是指将各部分净雨汇集到出口断面排入城市河网和雨水管网的过程(张配亮，2007)。研究中，对管道排除的水量以相应排水区块的设计排水能力进行概化处理，模型考虑了城市地表高程以及建筑物分布对地表径流的影响，利用等体积法模拟暴雨内涝的积水区域和积水深度。对于单个排水区块，t时段内的总径流量计算如下：

$ \Delta {{W}_{t}}=\left\{ \begin{align} & {{Q}_{\rm{add}}}+\frac{\sum\limits_{i=1}^{n}{\left( {{P}_{t}}-\Delta {{F}_{t}}-{{Q}_{\rm{pipe}}}t \right){{S}_{i}}}}{1000}\ \ \ \ \mu =1 \\ & \ \ \ \ \ \ \ \ \ \left( t=1,2,\cdots ,n \right) \\ & {{Q}_{\rm{add}}}+\frac{\sum\limits_{i=1}^{n}{\left( \Delta {{R}_{t}}-{{Q}_{\rm{pipe}}}t \right){{S}_{i}}}}{1000}\ \ \ \ \mu =0 \\ & \ \ \ \ \ \ \ \ \ \ \left( t=1,2,\cdots ,n \right)\ \ \\ \end{align} \right. $

(9)

式中，μ代表土地利用类型，若为透水区，则μ=1，若为不透水区，μ=0；ΔW_t为t时段内该排水区块的总径流量(单位：m³)；P_t为t时段的降雨量(单位：mm)；ΔF_t为t时段的累积下渗(单位：mm)；ΔR_t为t时段的累积产流(单位：mm)；Q_pipe为排水量(单位：mm·min^-1)；t为降雨历时(单位：min)；S_i为像元面积(单位：m²)；n为排水区块内所含像元数；Q_add为建筑体积修正量(单位：m³)，其初始值为0。研究在得到排水区块总径流量的基础上，设置模拟水深的增加步幅为0.01 m，采用等体积法迭代计算该排水区块的内涝积水深度。

依据《民用建筑设计通则》(JGJ37—2007；中华人民共和国建设部，2007)，建筑物室内地面宜高出室外地面0.15 m，但棚户等旧式住宅往往并不满足这一设计要求。考虑到建筑物离地高度与建筑年代、建筑层数存在一定关联，因此，在参考前人研究(尹占娥等，2010；景垠娜，2010)的基础上，本文对不同类型房屋分别设置离地高度值参与运算(表 1)。如果积水深度尚未达到建筑离地高度，建筑内部未受淹，则逐像元累加得到建筑体积修正量Q_add(式10)，并迭代计算式(9)；反之，则认为积水已漫入建筑物底层。

$ {{Q}_{\text{add}}}=\left\{ \begin{align} &\sum\limits_{i=1}^{n}{{{H}_{i}}{{S}_{i}}\ \ \ \ \ \ \ \ \ \ \ \ \mu =1\left(i=1, 2, \cdots, \mathit{n} \right)} \\ &0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mu \text{=0} \\ \end{align} \right. $

(10)

式中，μ代表土地利用类型，若为建筑，则μ=1，反之，则μ=0；n为汇水区内所含像元数；H_i为积水深度(单位：m)；S_i为像元面积(单位：m²)。

在降雨初期，由于地表的下渗作用较强，产流较小，往往不容易产生积水，而随着降雨的持续，产流量迅速增大，内涝范围也明显增加，模型运算中，如果上一时段的径流量ΔW_t-1＞0，那么考虑到径流量的叠加效应，在计算式(9) 时需要累加其上一时段的径流量迭代计算；同样，在降雨后期，雨量减小，内涝积水开始逐渐消退，此时ΔW_t趋于减小并逐渐变为负数，因此该时段的径流累加量也逐渐减小，并重新趋于0。在模型运算中，为了与短时临近格点化预报产品的时效相匹配，选用1 h时间间隔进行连续模拟，通过输入1~24 h的逐小时雨量，即可分别计算得到相应时次的城市内涝模拟结果。

2.3 城市设计暴雨雨型研究

在城市内涝的模拟过程中，除了考虑总雨量以外，降雨的时程分布形式也是决定内涝的重要影响因素。由于降雨量的大小显著影响径流的产生，而地表径流的损失随时间逐渐减小并最终趋于稳定，所以当降雨量越大或当雨峰的位置越向降雨总历时的后端推移时，暴雨所产生的径流峰值也越大(任伯帜，2004；岑国平，1989)。由此可见，在城市内涝估算中需要首先考虑降雨过程的时间分布，即雨型对城市地表径流的影响。

目前常用的设计雨型有CHM法(也称KC法)、Huff法、Yen & Chow法和Pilgrim & Cordery法。根据岑国平和沈晋(1998)的比较分析，国内适用性较好的合成暴雨模型是由Keifer和Chu提出的芝加哥雨型(CHM)，研究表明，该雨型过程线对任何暴雨历时的降雨均适用，假设暴雨强度公式为：

$ i=\frac{A}{{{\left(t+b \right)}^{n}}} $

(11)

式中，i为t时段内的平均雨强(单位：mm·min^-1)。由式(11) 可求得t时段内的总降雨量为：

$ H=it=\frac{At}{{{\left(t+b \right)}^{n}}} $

(12)

用时刻t对该时段内的降雨量求导，得出t时刻的瞬时雨强为：

$ I=\frac{\rm{d}\mathit{H}}{\rm{d}\mathit{t}}=\frac{A[(1-\mathit{n})\mathit{t}+\mathit{b}]}{{{\left( t+b \right)}^{n+1}}} $

(13)

式中，H为t时段内的总降雨量(单位：mm)。在芝加哥雨型中，降雨过程的雨峰出现在降雨开始后其历时的某一比例r处。研究中将降雨过程线分为峰前降雨和峰后降雨，其过程线分别用式(14) 和式(15) 表示：

$ {{I}_{1}}=\frac{A}{{{\left(\frac{{{t}_{1}}}{r}+b \right)}^{n}}}\left(1-\frac{n{{t}_{1}}}{{{t}_{1}}+rb} \right) $

(14)

$ {{I}_{2}}=\frac{A}{{{\left(\frac{{{t}_{2}}}{1-r}+b \right)}^{n}}}[1-\frac{n{{t}_{2}}}{{{t}_{2}}+(1-r)b}] $

(15)

式中，I为瞬时降雨强度(单位：mm·min^-1)；t₁为峰前历时(单位：min)；t₂为峰后历时(单位：min)；r为雨峰相对位置，即雨峰系数；A、b、n均为暴雨强度公式参数。研究中，根据2014年上海市气候中心^*给出的上海市暴雨强度公式(式16) 即可得到式(11) 中相应的参数值：

$ \mathit{i}=\frac{8.8112+7.8717\lg {{T}_{e}}}{{{\left(t+6.1005 \right)}^{0.6453}}} $

(16)

^* 上海市气候中心,2014.上海市暴雨强度公式研究.

式中，i为设计暴雨强度(单位：mm·min^-1)；t为降雨历时(单位：min)；T_e为设计降雨重现期(单位：a)，研究中雨峰系数r取0.398(宁静，2006)。

3 结果与分析 3.1 暴雨内涝情景模拟与致灾阈值分析

在构建城市内涝模型的基础上，本研究分别模拟了1、3和6 h不同降雨情景下的城市内涝分布，其中对于3和6 h的模拟采用上述芝加哥雨型作为输入。

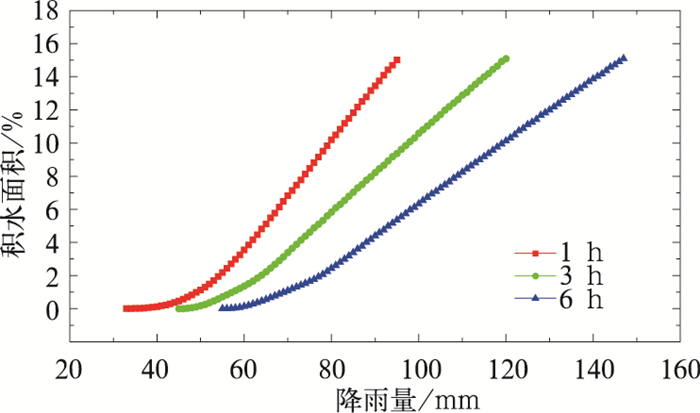
图 1中颜色深浅表示不同的内涝积水深度，可以看到，不同降雨情景下本市中心城区的内涝状况存在显著差异，而随着降雨量的增大，积水面积呈现出显著增加的趋势，且增幅逐渐变大(图 2)。由图 2可知，随着降雨历时的增加，中心城区的内涝致灾雨量也随之增大。当小时雨强达到33 mm时，中心城区部分低洼地区就已经开始积水，而对于分别历时3和6 h的降雨而言，这一致灾雨量值分别提升至45和55 mm；同样，1 h 95 mm以上的降雨和6 h 147 mm以上的降雨均可造成中心城区严重的城市内涝(积水面积超过15%)，由此可见降雨越集中，总雨量越大，城市就越容易遭受暴雨内涝灾害。

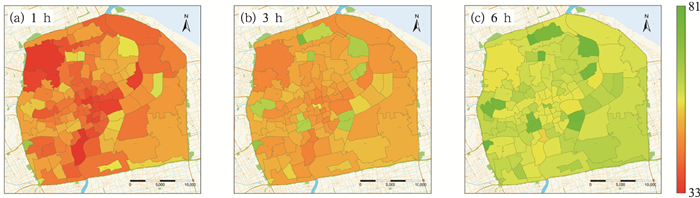
为了进一步评估本市中心城区的暴雨内涝脆弱性特征，研究分别针对区内各个街道开展了暴雨内涝致灾阈值的研究。图 3分别是针对1、3和6 h暴雨过程的街道致灾雨量图，从图中可知浦西地区的内涝致灾雨量总体上低于浦东，其中黄浦、徐汇、虹口和闸北等中心城区以及宝山区部分街道的致灾雨量相对较低。由于上述中心城区房屋建筑密集，不透水面积较大，雨水滞留与调蓄功能相对较弱，加之20世纪由于大量抽取地下水造成的地面沉降等原因，因此上述地区在暴雨来临时更易受灾。

3.2 暴雨内涝模型的检验

2013年9月13日午后，上海地区发生强对流过程，中心城区局地雨量达大暴雨，导致了城区多处内涝积水，由于强降水发生在下班高峰时段，给城市交通造成了严重影响。本研究针对该次暴雨内涝过程进行了内涝模拟，并依据报警灾情数据和区内部分积水监测数据对本文内涝模拟结果进行了评估。研究所用面雨量基于中心城区199个自动站(雨量站)插值得到；灾情数据来源于上海市气象局公共服务平台接入的二级公安接警系统，积水监测数据则来源于上海中心气象台于2012年在杨浦区建立的四个积水监测站。

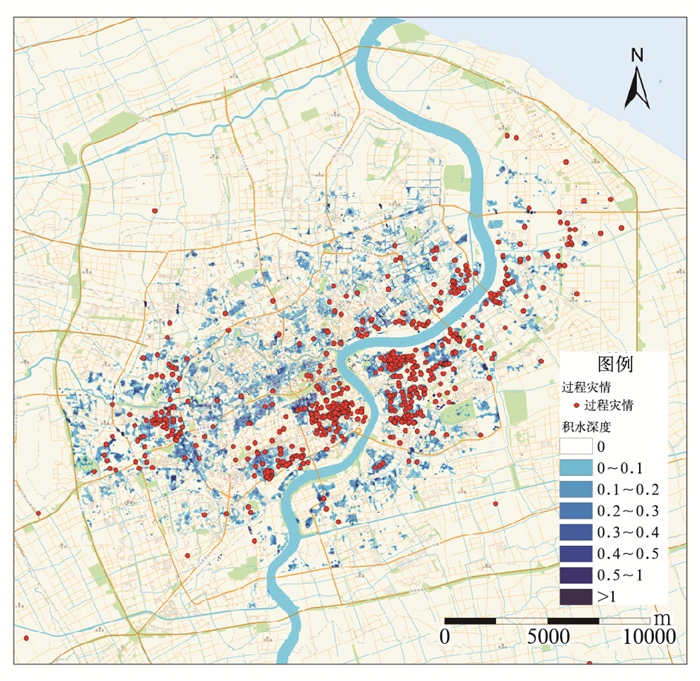
图 4为2013年9月13日强降雨过程的内涝模拟结果及灾情分布图，从图中可以看到该次过程的灾情主要集中在上海市黄浦区、浦东新区中西部以及长宁和徐汇区部分地区，其中位于浦东新区的崂山新村、招远小区、潍坊新村以及徐汇区东安新村等小区受灾较为严重，经调查，上述小区均为20世纪80年代前竣工的老式公房，由于地势低洼和排水不畅等原因造成上述小区暴雨内涝灾害频发。图 4中蓝色部分为模拟得到的内涝积水区域，可以看到本研究模拟的城市内涝区域与上述灾情高发区较为吻合。此外，由于报灾位置大多基于基站定位方式获取，对于城市区域一般情况下其定位精度可达50~200 m(王胜波等，2012)，因此本文取50 m缓冲区，分析其与模拟结果的匹配程度。结果表明，在接报的823起灾情中有617起与模拟结果相一致，模拟准确度达到74.97%。因此，本研究可以较好地模拟本市中心城区在一定降雨强度下的内涝空间分布，其准确度可以满足一般的业务需要。

在与报警灾情进行对比分析的基础上，本研究还采用区内积水监测数据对模拟结果进行了定量评估，本文所用积水监测数据分别取自杨浦区八一小区、多伦小区、商业一村和玉田新村四处积水监测站。从表 2中可知上述四处积水站在此次暴雨过程中均不同程度受淹，其中商业一村和玉田新村站的积水最深，达13 cm。从表 2中可以看到，模拟结果相比实测内涝积水数据均存在一定的偏差，误差最大值出现在多伦小区站，为4.95 cm，四个站点的平均相对误差为30.18%，可见利用该模型得到的积水深度与实测结果大体吻合。

4 结论与讨论

研究基于外环以内中心城区范围构建了SUM，通过对1~24 h内的不同降雨情景进行模型计算，即可得到相应的积水范围和积水深度信息。在此基础上，充分利用现有报警灾情资料和区内积水站数据对模型模拟结果进行了评估。结果表明，本研究所用SUM模型对暴雨内涝的空间分布和积水深度的模拟准确度分别达到74.97%和69.82%，模拟结果与实际内涝积水情况大致吻合，模型准确度可以满足一般的业务需要，同时也为暴雨内涝的影响预报和风险评估提供了一定的技术支撑。

通过分析内涝模拟结果可以得到，不同降雨情景下本市中心城区的内涝状况存在显著差异，而随着降雨量的增大，积水面积的增幅逐渐变大。当小时雨强达到33 mm时，中心城区部分低洼地区就已经开始积水，而对于分别历时3和6 h的降雨而言，这一致灾雨量值分别提升至45和55 mm。此外，研究还针对区内各个街道开展了暴雨内涝致灾阈值的研究，结果表明，浦西地区的内涝致灾雨量总体上低于浦东，其中上海市黄浦、徐汇、虹口、闸北等中心城区以及宝山区部分街道的致灾雨量相对较低。由于上述中心城区房屋建筑密集，不透水面积较大，雨水滞留与调蓄功能相对较弱，加之20世纪由于大量抽取地下水造成的地面沉降等原因，因此上述地区在暴雨来临时更易受灾。

本文在缺乏研究区排水管道相关数据的情况下，通过对管道排水量进行概化处理，不仅解决了数据缺失导致无法搭建水力学模型的问题，更显著缩短了模型的运算时间。在此基础上，SUM模型实现了1~24 h内逐小时的连续模拟，使得影响预报中模型的实时运算成为可能。研究还充分利用现有灾情资料和积水监测站数据对模拟结果进行评估，也为此类研究提供了一个新的思路。此外，由于上海市滨江临海，当河道水位过高，雨水系统排水能力超过河道承载能力时，雨水泵站往往被迫停机，从而大大降低区块排水能力，当前对河道水位和排水能力的相关关系研究较少，因此，对于“风暴潮洪”多碰头下的城市内涝模拟还有待进一步研究。