2. 中国民用航空华北地区空中交通管理局,天津 300074
2. Air Traffic Management Bureau in North China of CAAC, Tianjin 300074
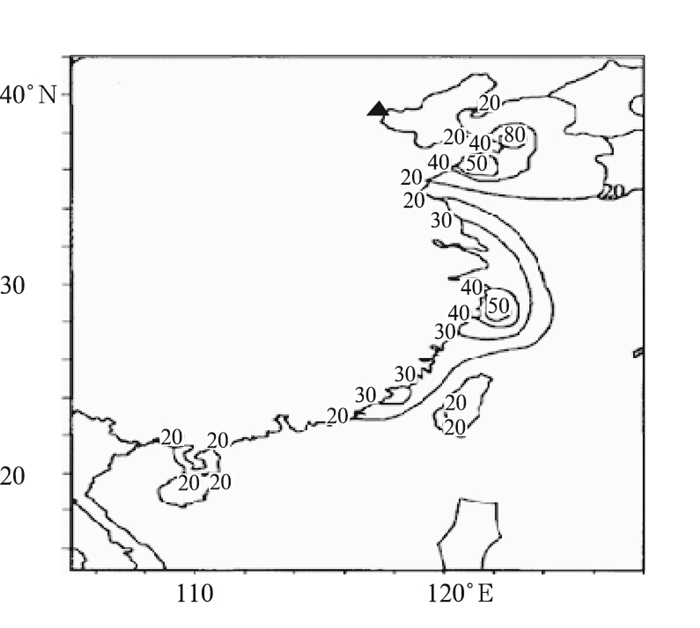
低能见度对港口经济生产、交通安全影响甚大,是港口防灾减灾非常关心的天气现象。低能见度的出现与雾、降水、霾和沙尘等天气现象有关(闫俊岳等,1993),其中大雾是影响港口能见度最主要的天气现象,据统计海上碰撞事件有80%是由于雾所导致的能见度不良而引起的(钱之光,2010)。雾具有明显地域性和季节性特征,生成机制复杂,预报难度大,因此对大气低能见度的预报研究一直是近年来气象预报中的一个难点和热点。天津港地处渤海湾西海岸(图 1),位于中国天津市海河入海口(38°59′08″N、117°42′05″E),在京津冀城市群和环渤海经济圈的交汇点上,是中国北方最大的综合性港口和重要的对外贸易口岸。突如其来的大雾天气,常常使得港口运营停滞,如2011年2月20—23日,渤海湾遭遇持续43 h的浓雾天气,海面最大能见度不足10 m,使得船舶停滞在港湾,同时大量船舶无法进港,带来严重的经济损失。港口大雾低能见度事件对港口经济发展的影响如此之大,因此对其提前预知的需求非常迫切。
|
图 1 我国近岸年雾日频数(单位:d·a-1) (张苏平和鲍献文,2008;▲为天津港位置) Fig. 1 The annual frequency of coast fog in China (unit: d·a-1) (▲ denotes the site of Tianjin Port) |
低能见度的常见预报方法目前有两大类,一类是依托对影响能见度的各因子消光特性的反演,这些因子有云水、云冰、霰和气溶胶等各类物质。数值模式预报输出的能见度常采用该方法,中尺度数值天气模式中,依托云水、云冰、霰等水凝物的消光性质来反算能见度(Gultepe et al,2006),其缺点是由于没考虑气溶胶变化的影响,对非过饱和条件下的低能见度天气几无预报能力;而加入了气溶胶影响的大气化学模式,由于对气溶胶的源汇及其扩散处理不好,能见度预报准确率也仍然离服务需求有较大差距(Tudor,2010)。另一类是通过寻找宏观要素对能见度的影响关系,构建预报量(能见度)与预报因子(风、温、压、湿、气溶胶因子等)之间的统计模型。日常预报业务中,常结合数值模式预报的各气象因子与实况能见度,建立统计预报方法,开展大雾和低能见度预测,既弥补了前种方法的不足,又充分利用了数值模式预报基本气象要素的优势。目前数值预报释用技术较多采用方法包括卡尔曼滤波方法(佟华等,2014)、支持向量机方法(丁煌等,2013)、模糊逻辑(Hansen,2007; 张芳华等,2016)、人工神经网络(ANN)(陆虹等,2015),其中人工神经网络因具有较好的自学习功能及处理非线性问题的能力,应用在大雾和低云预报方面效果突出。Marzban et al(2007)曾利用模式输出产品和地面逐时观测资料,对比了MOS方法、多元回归方法和神经网络方法对美国东北机场低能见度的预报能力,证实了利用神经网络方法的优势。该方法在国内大雾预报也得到成功应用,如李法然(2005)应用BP神经网络较好地建立湖州市大雾预报模型,马学款等(2007)建立的神经网络模型明显提高了对重庆市区雾天气的预报能力。李沛等(2012)基于神经网络逐级分类建模开展了北京地区能见度预报,取得了很好的预报效果。随着海洋经济的发展,国内外颇重视对港口雾的研究,国外如加利福尼亚港口雾的天气预报技术研究(Leipper,1995),国内如宁波港(钱之光,2010)、湛江港(杨彩福等,1998)以及华南沿海大雾(黄健等,2010)的特征与预报技术也有一些研究成果。前人研究尚未见天津港口低能见度预报技术的相关研发;已有文献中即便使用神经网络方法开展低能见度预报建模研究,也多采用日最低能见度观测资料,分级为雾日、非雾日,并没有针对逐时能见度的业务预报和检验结果;另外,文献中预报效果检验测试时间比较短,且多为个例检验(王彦磊等,2010),或者检验时间只有一个月(李沛等,2012),最长的检验时间也不到两年(王雷和黄培强,2001)。
本文针对天津港低能见度天气,在对其近年来高频能见度资料进行分析特征认识基础上,使用2006—2012年10月至次年3月的逐日资料,分全样本、1.5~3.5 km和0~1.5 km 3个不同区间能见度的样本,基于神经网络方法,对同时次的相关物理量和能见度数据训练建模。该方法实际上是利用当前时次的风、温、压和湿等物理量要素或相关要素来反演同时刻的能见度值。业务应用该组模型时,采用分步筛选法逐层预判能见度值,实现了天津港72 h时效逐时的能见度业务预报。该方法2013年投入业务应用,本文检验时段为2013—2015年的10月至次年3月逐时能见度预报结果。
1 天津港大气能见度分级统计特征以前对渤海沿岸雾日统计的文献中,是基于人工3~4次·d-1的观测资料,统计特征难免与实况有出入(林之光,1987)。鉴于近几年布设了能见度自动观测仪器,本文利用能见度仪的高频观测资料分析天津港地区能见度分布特征。能见度仪所在自动站(标号A3174) 地理位置为39°04′12″N、117°32′18″E,观测仪器采用VaisalaQML201型数据采集器,由天津市气象局装备中心负责设备检定和维护。本文采用2009年7月建站以来至2013年5月逐10 min的能见度观测资料,按照4—9月夏半年(主要为春、夏季节)、10月至次年3月冬半年(主要为秋、冬季节)两季,以及细分白昼(08—17时)、夜间(18时至次日07时)两时段来统计。根据航船对能见度的需求调研得知,能见度<1 km时,对大部分船舶有很大影响;能见度<3 km时,对大型船舶也有较大影响。因此,本文对能见度<10 km进行分级精细统计,以便为不同行业预报服务提供依据;而能见度≥10 km时,因不再对港口经济活动有影响,故不再细分。
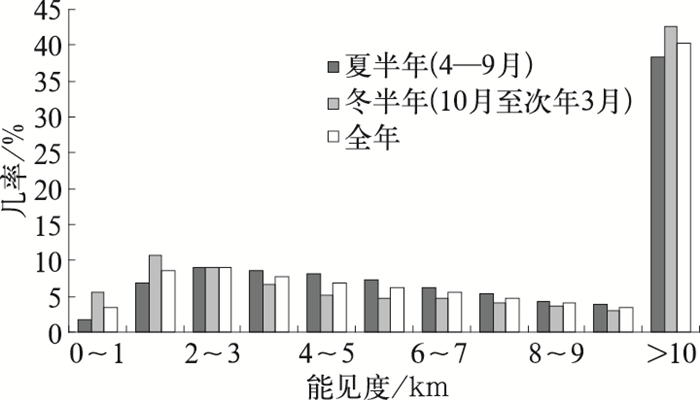
全年各级能见度几率分布见图 2。就全年看,10 km以上能见度出现的几率约为40.3%;2~10 km(表示≥2且<10,全文类同)各区间能见度出现的几率由9.0%逐次递减到3.5%,合计约为47.7%;<2 km的能见度合计约12%。从各季看,对<1 km严重影响港口及海上航运的能见度,夏半年出现几率约1.6%,冬半年约5.6%;对于1~2 km对大型船舶有影响的低能见度,在冬半年均比夏半年出现几率大,夏、冬季分别约为6.9%和10.7%;>10 km的高能见度在不同季节的分布规律与影响交通的低能见度类似,冬半年出现更频繁,高出约4%;2~3 km在冬、夏半年出现几率相当;而4~10 km中间区间能见度的季节差异与高、低能见度出现规律相反,冬半年比夏半年出现几率约小1%~3%不等。能见度分布这种季节差异与稳定小风和冷空气大风两种极端天气主要出现在秋、冬季节相对应,因稳定小风条件下易出现雾-霾低能见度天气,而冷空气大风时空气清洁往往对应高能见度天气。
|
图 2 各级能见度在冬、夏半年和全年出现分布几率 Fig. 2 Probability distribution of visibility value for summer, winter and the whole year |
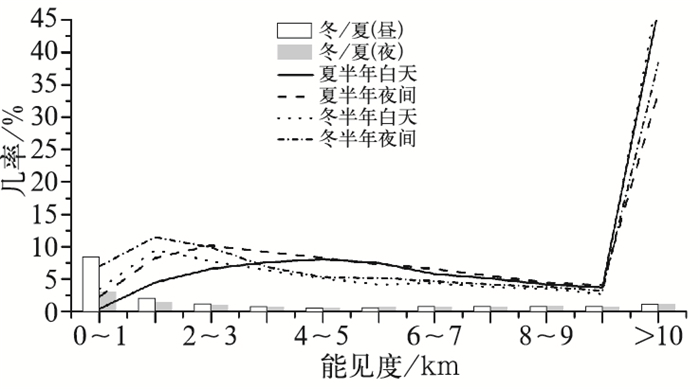
区分白昼、夜间来分析各级能见度的分布情况(图 3),总体来看,10 km以下的低能见度,全年白昼出现几率低于夜间,>10 km的高能见度分布趋势相反。其中,0~4 km能见度的昼、夜出现几率差别在2%~4%;4~10 km能见度的昼、夜出现几率差别不到1%;10 km以上能见度,夏(冬)半年白昼出现的几率大于夜间12.8%(10.8%)。具体而言,对于<1 km的能见度,夏(冬)半年白昼出现几率很小,分别为0.4%(3.5%),夜间为2.3%(7.0%);对于1~3 km的低能见度,夏(冬)半年白昼几率分别为11.1%(17.3%),夜间分别为18.4%(21.3%)。无论在哪个季节,低于3 km影响交通的低能见度白天均比夜间出现几率小,且1 km以下的能见度,白昼时段秋、冬季节出现几率是春、夏季节的近9倍,夜间时段约为3倍。这种差异与气温、相对湿度和污染物等多种主要影响因素的日夜分布规律息息相关。
|
图 3 各级能见度在昼、夜出现分布几率及冬、夏半年比率分布 Fig. 3 Probability and ratio distribution of visibility value during daytime and nighttime |
BP神经网络全称是误差反传(error back propagation)前向网络,在1986年由Rumelhart和McCelland为首的科学家小组提出,它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权重值和偏移值,使网络输出值与期望值的误差平方和最小。其基本原理是:网络把一系列输入经过联接权重加权输送给隐含层,隐含层各神经元汇总所有输入后,通过转移函数产生某种响应输出,并通过下一层联接权重加权输送给输出层。输出层各神经元汇总所有输入后产生响应输出。然后再将其输出与期望输出进行比较。若两者趋于一致或相差甚小,可认为完成了网络训练。若相差较大或不够满意,便将网络输出与期望输出两者间的误差送回,通过调整各联接权重进行重复的训练学习,如此循环直至其他能产生逼近真实答案的输出结果为止。相对传统的数理统计方法而言,BP神经网络优势是既可以求解非线性问题,又不要求样本独立或遵从正态分布(阎平凡和张长水,2000)。本文采用算法较成熟、应用较广泛的前向BP网络算法,包括输入层、隐含层和输出层三层。神经元之间的激活函数选取Tansig函数,Tansig函数的定义式为:
| $ \rm{Tansig}\left( \mathit{x} \right)=2/\left( 1+{{\rm{e}}^{\rm{-2}\mathit{x}}} \right)-1 $ | (1) |
定义神经网络的输出为y,那么
| $ \begin{align} & \mathit{\boldsymbol{y}}=\rm{Tansig}\{\mathit{\boldsymbol{Lw}}\left( 1 \right)\times \rm{Tansig }[\rm{ }\mathit{\boldsymbol{Lw}}\left( 1 \right)\times \mathit{\boldsymbol{p}}\rm{+} \\ & \ \ \ \ \ \ \mathit{\boldsymbol{b}}\left( 1 \right)]+\mathit{\boldsymbol{b}}\left( 2 \right)\} \\ \end{align} $ | (2) |
式中,Iw(1) 是网络输入层权重值矩阵,Lw(1) 是网络隐层的权重值矩阵,b(1) 为网络输入层偏移量矩阵,b(2) 为网络隐层偏移量矩阵,p为各个网络的输入量。
在网络结构确定的情况下,神经网络的训练过程实际就是不断调整Iw(1)、b(1)、Lw(1)、b(2) 的值,以使网络计算结果和期望值的误差平方和最小。
2.2 建模因子选取与模型训练 2.2.1 因子选取思路建立低能见度预报天气学概念模型时,较多强调高、低层环流形势的组合,为了实现能见度预报的客观化处理,必须将高、低层环流背景做量化处理,一般应用多个气象要素组成的物理量提取各种环流背景下的主要特征,方便量化预报因子,实现预报的客观化和自动化。以往的预报建模思路,多采用过去的实况气象要素预报未来能见度的可能情况(王彦磊等,2010; 李沛等,2012)。本文模型构建的思路为用当前的气象要素来判断当前能见度值,即用当前物理量因子反演同期的能见度值。尽管污染因子对能见度影响很大(蔡子颖等,2012),因该港口气溶胶观测时间短,不适用于统计分析,故本文仅考虑气象因子对能见度的影响。
由于本地WRF中尺度天气模式产品没有保存足够的样本,本文选用2006—2012年的NCEP资料,结合同时段逐日08时的自动气象站资料,并用本站地面观测资料取代NCEP资料中的2 m的气象要素,计算出表征大气稳定度、水汽、气压场变化以及动力、热力作用的40个单物理量或组合物理量来量化环流背景的特征。其中表征动力作用的物理量,如:1000 hPa垂直速度、10 m全风速、10 m南北向风、1000 hPa南北向风;表征大气热力条件和温度层结的,如:位温、不同高度层的位温差;表征水汽条件的物理量有:各层温度露点差和各层温度平流等。
将初步选取的40个物理量因子与对应的大气能见度逐一作单因子相关分析,采用SPSS 13.0统计软件计算每个因子与大气能见度值之间的皮尔逊相关系数,确定了13个相关系数≥0.3的高影响物理量,均通过了α=0.05的显著性水平检验(表 1)。这些被选入的高影响因子大多为大气低层物理量,如地面南北向风速、地面全风速、925 hPa南北向风速、地面24 h变压代表大气低层动力作用,大气动力混合作用强,有利于大气能见度变好;低空K指数以及925 hPa垂直速度代表低空大气动力热力垂直混合条件,低空垂直混合强,水汽和污染物容易向高层输送,有利于大气能见度变好;925 hPa的位温、925与1000 hPa位温差及1000 hPa与地面位温差代表低层热力状态及热状态的垂直差异,主要反映大气层结,层结稳定时,容易出现低能见度天气,是影响低层大气能见度的主要因素;1000 hPa与地面层的温度露点差及1000 hPa的湿度平流,代表低层大气水汽条件和水汽变化趋势,水汽含量是影响能见度的关键因素;M指数表征上干下湿的大气层垂直配置(马学款等, 2007),上干下湿条件容易出现低能见度天气。由表 1可以看出,能见度与地面全风速、925 hPa垂直速度、24 h地面变压、低层的温度露点差以及M指数呈正相关,即动力混合越强,湿度越小,能见度越好;能见度与低层南北向风速、低层位温梯度、925 hPa位温、低层湿度平流呈负相关,即低层南向风有利于湿度加大,表明了低层大气增湿、增温,有利于低能见度天气形成。
|
|
表 1 对能见度有高影响的气象因子及其中位值 Table 1 Median value and correlation coefficient for meteorological factors related highly to low visibility |
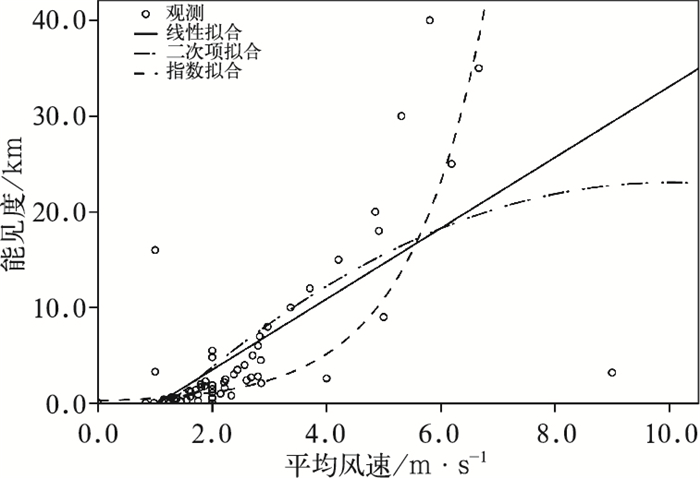
对以上13个因子与能见度值进行单因子最优关系拟合,发现每个因子与能见度之间均存在复杂的非线性关系,利用任一给定的数学模型进行拟合均存在很大局限。如为了查看能见度与地面风速之间的关系,分别将两者进行了线性、二次项、指数等多种数学模型拟合,发现尽管指数拟合关系相对较优,但其拟合度并不理想(图 4)。这说明能见度的大小与这些影响因子之间存在未知的复杂关系,鉴于神经网络模型擅长处理复杂的非线性关系,因此下文应用神经网络方法建模预报能见度,预期能得到较好的预报结果(Marzban et al,2007)。由于低能见度天气是小概率事件,天津港能见度<3 km的几率不到17%。因此,在样本处理过程中,只是排除降水和沙尘的影响,不再区分天气系统,这种处理方法可能增加了网络的学习难度,但更方便实际业务工作中应用。
|
图 4 能见度与风速的多种数学模型拟合关系 Fig. 4 The fitting relationship of visibility and wind speed |
用表 1中13个高影响因子,采用BP神经网络方法,进一步构建能见度与预报因子之间的定量关系。经多次试验表明,由于低能见度是低概率事件,如果仅利用一个神经网络对所有样本进行建模识别,其仿真效果很难对样本中的低概率事件具有高敏感性。因此,本文采用了对不同区间能见度样本分别进行建模训练的方法,以期建立低能见度预报的最优模型。
经反复试验,最终选择的建模思路如下:排除沙尘和降水资料,选用2006年以来连续7年10月至次年3月逐日08时的能见度样本,通过训练建立粗分神经网络模型;再用该时间段内所有能见度<2 km的个例组成样本库,通过训练建立低值神经网络模型;最后挑选出所有能见度在1.5~3.5 km的样本,通过训练建立中间神经网络模型。
由于样本选择不同,对能见度大小有高影响的因子也会有相应变化,故针对不同区间能见度样本重新分别开展了因子分析,以确定每个网络的输入变量。对每组样本,分别选择相关系数绝对值较大,且物理意义明确的物理量进入对应的神经网络。
训练前,由于各物理量单位不一致,因而需对数据进行归一化处理,归一化方法采用线性函数转换到[-1,1]区间,表达式如下:
| $ \mathit{y}=\frac{2\left( x-MinValue \right)}{MaxValue-MinValue}-1 $ | (3) |
式中,x、y分别为第i个因子转换前后的值,MaxValue、MinValue分别为总样本中第i个因子的最大值和最小值。
经因子分析和对问题复杂度的估计,采用每个神经网络的输出层只有一个神经元。隐层神经元的数目在经验公式的指导下,通过反复的训练来确定。最终,粗分网络隐层有8个神经元,进入模型的物理量有10个,分别是:925 hPa垂直速度、10 m南北向风、925 hPa南北向风、地面24 h变压、925 hPa位温、1000 hPa与地面位温差、低空K指数、1000 hPa温度露点差、地面温度露点差、M指数。训练得到神经网络输入层的权重值Iw(1) 和偏移量系数b(1),以及神经网络隐层的权重值Lw(1) 和偏移量系数b(2)。
低值网络隐层有9个神经元,进入模型的物理量有4个,分别是:10 m风速、1000 hPa与地面位温差、地面温度露点差和M指数。
中间值网络隐层有13个神经元,进入模型的物理量有2个,分别是:1000 hPa与地面位温差、地面温度露点差。
从各层网络进入模型的物理量看,代表地面动力作用、低层湿层厚度、上干下湿配置以及层结稳定特征是影响低能见度的最主要原因。
2.2.3 模型分步筛选识别预报思路建模采用的NCEP再分析资料,如果将训练好的模型对接该资料,将无法满足业务及时性要求,故将训练的3个BP神经网络预报模型直接与WRF输出产品对接,于2013年初正式业务应用。对应建模中用到的925和1000 hPa的高度,分别取WRF中对应高度相应δ层的预报值,直接计算WRF预报产品中各δ层每个格点的13个物理量(表 1),然后输送到相应网络模型中。因本地WRF业务模式每日运行2次,每次有72 h预报时效,针对WRF模式逐时的预报产品,利用训练好的3个神经网络模型,按图 5中步骤进行能见度逐步筛选预报,即:
|
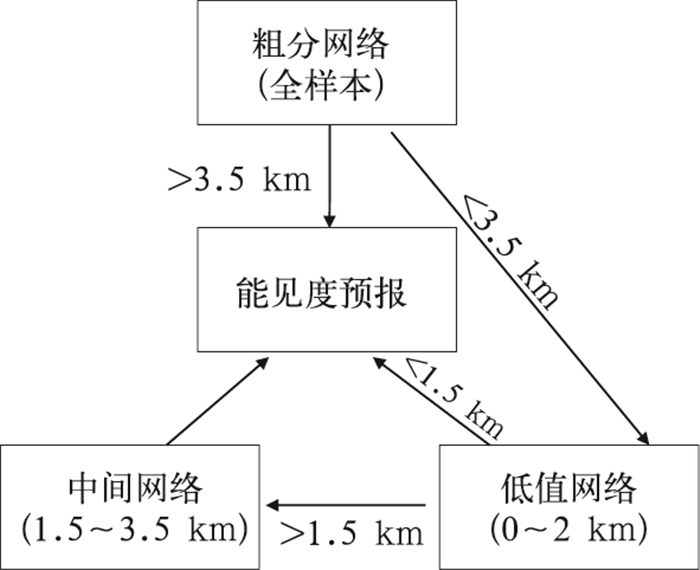
图 5 3重神经网络分步筛选预报的技术路线 Fig. 5 Process of simulating forecast using three neural networks |
第一步:先用粗分神经网络对输入的预报因子进行预报,如果预报值在3.5 km以上,则采用这个网络得到的结果,否则进入第二步。
第二步:对于粗分神经网络预报值在3.5 km以下的个例,进一步用低值神经网络进行预报,如果预报值在0~1.5 km,则采用此值,否则进入第三步。
第三步:对于用低值神经网络预报值在1.5 km以上的个例,再次采用中间神经网络进行预报,得到最终预报值。
各个模型按照式(2) 计算,得到每个输入向量对应的输出y值。计算后得到的y值按式(1) 的逆运算,求解x值,即为模拟预报得到的能见度值。
为了方便叙述,下文中将利用该3个神经网络模型对接WRF模式产品进行逐步筛选方法输出的能见度数值释用产品简称为BPTFP(back propagation three filter product,下同)。
3 业务应用检验下文给出2013年正式投入业务运行以来10 km以下能见度的预报命中率。基于有些行业对能见度预报精度要求较高,将10 km以下低能见度的检验范围分为7级,划分范围依次为0~0.5 km (不包含0.5 km,下同)、0.5~1、1~2、2~3、3~4、4~5和5~10 km。某级别的命中率计算公式如下:
| $ Hi{{t}_{j}}=\frac{N{{A}_{ij}}}{N{{A}_{ij}}+N{{B}_{ij}}+N{{C}_{ij}}}\ \ \ \ j=1, 2, \cdots, 7 $ | (4) |
式中,Hitj为第j级别能见度的命中率,NAij为第i个个例第j级能见度的预报击中次数,NBij为预报偏大的次数,NCij为预报偏小的次数。
3.1 逐时预报效果检验 3.1.1 总样本逐时检验尽管建模时排除了实况有降水的样本,但业务预报应用时,实际难以预先准确判断WRF降水预报是否正确,实际可能无论是否预报降水,都会参考能见度BPTFP,那么哪个可信度更高呢?基于此考虑,本节检验3年业务运行的总体平均情况。
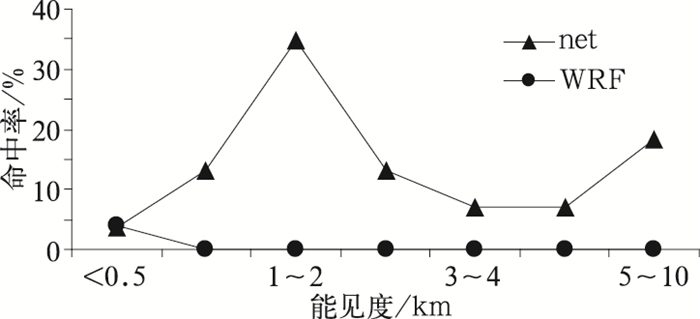
将10 km以下的能见度分为七级检验,从连续3年检验总体平均水平看,对于从小到大七个能见度级别的平均命中率,BPTFP检验分别为4%,13%,35%,13%,7%,7%,18%;而WRF模式预报检验评分,只有对<0.5 km的能见度有预报能力,与BPTFP评分相同,对其他级别能见度均无预报能力。表明对<0.5 km的能见度天气,BPTFP改进不明显,而对其他各级低能见度均比原WRF模式预报能力有大幅的提高(图 6)。
|
图 6 低能见度命中率总体平均检验结果 (net: BPTFP, WRF:模式预报产品,下同) Fig. 6 Total averaged average hit ratio of different visibility ranges for the whole three years |
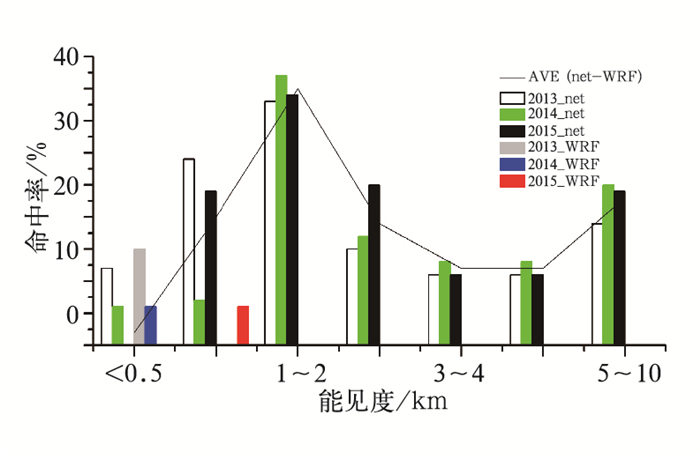
从逐年检验情况看(图 7),总体上秋、冬季BPTFP连续3年均比原WRF模式预报产品有稳定大幅的提高,除<0.5 km略低外,BPTFP比WRF命中率平均提高了7%~35%,尤其对0.5~2 km,平均提高了15%~35%。各年对逐时预报的检验情况如下:实况<0.5 km的能见度,两种方法预报命中率相当,WRF模式预报为0~10%,BPTFP为0~7%,其中仅2013年WRF模式对低能见度的预报略占优势,高出3%,2014—2015年两者预报技巧相同;实况0.5~1 km的能见度,WRF模式预报命中率为0~1%,BPTFP命中率提高到2%~24%;对1~10 km的能见度,WRF模式接近0%,BPTFP命中率显著提高,其中1~2 km能见度预报命中率提高到33%~37%,2~3 km能见度预报命中率提高到10%~20%,3~5 km能见度预报命中率提高到6%~8%,5~10 km能见度预报命中率平均提高了14%~20%。
|
图 7 逐时能见度预报产品的逐年对比检验 (2013_net:2013年数值释用产品,2013_wrf:2013年WRF预报产品,以此类推,下同) Fig. 7 Constrast test of hit ratio for WRF and neural network model to visibility forecast from 2013 to 2015 |
因WRF模式后处理输出的能见度,是利用云水、云冰、雨雪和霰等水凝物的消光特性计算出来的,如果WRF预报有降水时,模式一定预报有水凝物,则其对应的能见度预报应该可信度较高,那么BPTFP是否还有优势呢?
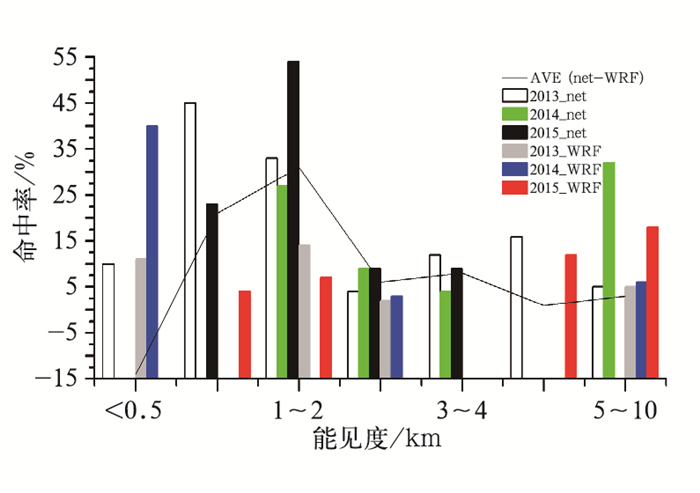
将同时段WRF预报有降水的全部样本提取出来,并取对应BPTFP进行统计检验比较(图 8)。可以看到:在WRF预报有降水的条件下,除<0.5 km外,BPTFP<10 km的各级能见度预报总体上比原WRF模式预报有提高,尤其对于0.5~2 km的,显著提高了21%~31%。对于实况<0.5 km的能见度,当样本量较大时(如2013年63个样本),两种方法预报命中率差异仅为1%;当样本量小时,如2014年(5个样本)和2015年(3个样本),WRF预报命中率分别为40%和0,BPTFP均没预报出来,说明对此级别的能见度,WRF模式原预报优于BPTFP产品。0.5~1 km的能见度,3年依次出现33、17和26次,除2014年均没有预报出来外,其他两年BPTFP命中率为45%和23%,WRF分别为0和4%,BPTFP命中率显著优于WRF。对于1~2 km的能见度(样本数3年依次为196、62和28次),BPTFP命中率依次为33%、27%和54%,比WRF各年命中率提高了19%~47%不等;同样,对于2~4 km能见度,BPTFP也提高了2%~16%不等;但对于4~10 km能见度,两种预报各年表现不一,2013和2014年BPTFP命中率均优于WRF,但2015年相反。总之,即便在WRF模式预报有降水条件下,BPTFP对0.5 km以上的低能见度预报也显著优于WRF模式预报。
|
图 8 WRF预报有降水条件下的各级低能见度的预报命中率 Fig. 8 Constrast test of hit ratio for visibility of neural network model and WRF with rain forecast condition |
引言中已经提到已有文献对能见度的预报建模多采用日最低能见度观测资料,针对日最低能见度以1 km为分界线来检验对误。为了便于与已有文献结果对比,本节采用与文献类似的办法,以气象日界为标准,选取每日24个时次预报的最低能见度作为日最低能见度,分为<1 km和1~10 km两级进行日最低能见度检验(表 2)。可以看到,对<1 km的日最低能见度,WRF模式技巧评分为51%,BPTFP为75%,优于同类方法的有无雾预报技巧,如芜湖的技巧检验为33%(王雷和黄培强,2001),某机场的技巧检验为70%(袁志康等,2002),北京地区的技巧检验为60%(李沛等,2012);对于1~10 km的日最低能见度,WRF模式技巧评分为3%,BPTFP技巧评分大幅度提高到63%。
|
|
表 2 逐日最低能见度检验(单位:%) Table 2 TS score of daily minimum visibility for neural network model and WRF (unit: %) |
个例检验更能直观看出利用BPTFP的优越性,本文选取两次过程为例,第一次大雾过程出现在2013年1月21—24日,天津港持续两天多的大雾天气。1月21日20时72 h时效的能见度预报效果可直观看到(图 9a),BPTFP与实况趋势一致,提前72 h预报出了这次长时间大雾天气;而WRF给出的预报,仅在31~34 h时效内与实况一致,该时段内WRF同时预报有毛毛雨。第二次大雾过程出现在2013年2月3日,大雾同时伴随降雨天气(图 9b),在2月2日20时的WRF预报中,10~34 h预报时效内同时预报有小雨,故该段时间WRF预报能见度与实况较接近,其他时间预报与实况趋势相差甚远,而BPTFP的能见度趋势与实况基本一致,只是在12 h预报时效内,明显比实况偏低。

|
图 9 2013年1月21日(a)和2月2日(b)两次大雾过程检验 Fig. 9 Visibility forecast verification of neural network model and WRF for the two coastal fog cases on 21 January (a) and 2 February (b) 2013 |
介绍了天津港秋、冬季大气能见度的分级统计特征,分析了与之相关的气象影响因子,并应用2006—2012年地面观测资料和对应NCEP资料,基于人工神经网络方法,分别对不同区间的能见度预报构建了3个预报模型。对应WRF模式业务运行输出的基本物理量及二次计算产品,以逐级筛选方式实现了72 h时效的逐时大气能见度业务预报。分7个区间的能见度样本针对逐时低能见度预报、分2个区间的能见度样本针对日最低能见度预报,对比检验了2013—2015年秋冬季WRF模式预报和BPTFP的技巧评分情况,并且给出了2个低能见度过程的预报对比,结论如下:
(1) 天津港各级能见度分布不均,季节分布也有显著差异。全年<3 km的低能见度和>10 km的高能见度出现分别占12%和40.3%,3~10 km能见度占47.7%,且前者在秋、冬季节比春、夏季节出现机率大,其中秋、冬季能见度<1 km事件比春、夏季出现几率高4.0%。
(2) 影响能见度好坏的关键气象因素随建模样本不同有所差异。其中上干下湿的大气配置对能见度的影响始终显著,与建模样本无关;全样本能见度的影响因子主要位于低空,包括低层大气湿度、风速、垂直运动和气团稳定情况等;<2 km的低能见度的主要气象影响因素为地面风速、湿度以及低空大气的热状态差异;1.5~3.5 km能见度的主要影响因素为大气湿度以及低空大气的热状态差异。
(3) 基于人工神经网络方法对WRF数值产品开展逐时释用预报,释用产品与能见度实况日变化趋势接近,比原模式中消光计算方法得到的能见度产品预报技巧有很好改进。除<0.5 km的逐时预报技巧略低外,BPTFP连续3年秋、冬季对0.5~10 km的逐时预报技巧均比原WRF模式产品稳定提高了7%~35%,尤其对0.5~2 km,平均提高了15%~35%;对<1 km的低能见度过程技巧评分显著提高了24%,达到75%的命中率;对1~10 km的低能见度过程技巧评分提高了60%。
然而,在WRF预报有降水条件下,对于<0.5 km的能见度事件,BPTFP效果比WRF的消光计算方法得到的能见度略差。其可能原因大致如下:其一,对<0.5 km的大雾和1 km以下的雾事件来说,其气象要素及天气形势之间的差异很难辨别出来,即便本文采用了直接预报能见度的方法取代传统分类方法也难以分辨;其二,<0.5 km的大雾事件几率极低,样本不足,这种微细差异难以用统计预报方法表征出来,而且有云水、雨水等水凝物存在,才会导致如此恶劣能见度情况,消光计算能见度方法正好是利用不同水凝物的消光系数差异,因此比统计方法显示出其优越性。建议业务应用时,可以结合两种预报结果,只要有一种产品预报能见度<0.5 km则采信,如预报>0.5 km,则采信BPTFP产品。
蔡子颖, 韩素芹, 吴彬贵, 等, 2012. 天津一次雾过程的边界层特征研究[J]. 气象, 38(9): 1103-1109. |
丁煌, 陶树旺, 肖子牛, 等, 2013. 基于WRF和SVM方法的风电场功率预报技术研究[J]. 高原气象, 32(2): 581-587. |
黄健, 黄辉军, 黄敏辉, 等, 2010. 广东沿岸海雾决策树预报模型[J]. 应用气象学报, 22(1): 107-114. |
李法然, 2005. 湖州市大雾天气的成因分析及预报研究[J]. 应用气象学报, 16(6): 794-803. DOI:10.11898/1001-7313.20050604 |
李沛, 王式功, 尚可政, 等, 2012. 基于神经网络逐级分类建模的北京地区能见度预报[J]. 兰州大学学报:自然科学版, 48(3): 52-57. |
林之光, 1987. 中国气候[M]. 北京: 气象出版社.
|
陆虹, 翟盘茂, 覃卫坚, 等, 2015. 低温雨雪过程的粒子群-神经网络预报模型[J]. 应用气象学报, 26(5): 513-524. DOI:10.11898/1001-7313.20150501 |
马学款, 蔡芗宁, 杨贵名, 2007. 重庆市区雾的天气特征分析及预报方法研究[J]. 气候与环境研究, 12(6): 795-803. |
钱之光, 2010. 宁波港海区雾的成因和特点[J]. 中国水运, 10(3): 14-15. |
佟华, 郭品文, 朱建, 等, 2014. 基于大尺度模式产品的误差订正与统计降尺度气象要素预报技术[J]. 气象, 40(1): 66-75. DOI:10.7522/j.issn.1000-0534.2013.00073 |
王雷, 黄培强, 2001. 利用人工神经网络预报芜湖的雾[J]. 气象科学, 21(2): 200-205. |
王彦磊, 曹炳伟, 黄兵, 等, 2010. 基于神经网络的单站雾预报试验[J]. 应用气象学报, 21(1): 110-114. DOI:10.11898/1001-7313.20100115 |
闫俊岳, 陈乾金, 张秀芝, 等, 1993. 中国近海气候[M]. 北京: 科学出版社.
|
阎平凡, 张长水, 2000. 人工神经网络与模拟进化计算[M]. 北京: 清华大学出版社.
|
杨彩福, 吴阳, 张佃波, 1998. 湛江港雾的统计分析[J]. 海洋通报, 17(5): 34-39. |
袁志康, 张韧, 周树道, 等, 2002. 基于人工神经网络算法的某机场雾的模式识别预报[J]. 解放军理工大学学报:自然科学版, 3(4): 82-86. |
张芳华, 曹勇, 徐珺, 等, 2016. Logistic判别模型在强降水预报中的应用[J]. 气象, 42(4): 398-405. DOI:10.7519/j.issn.1000-0526.2016.04.002 |
张苏平, 鲍献文, 2008. 近十年中国海雾研究进展[J]. 中国海洋大学学报:自然科学版, 38(3): 359-366. |
Gultepe I, Mullerz M D, Boybey Z, 2006. A new warm fog parameterization scheme for numerical weather prediction models[J]. J Appl Meteor, 45(11): 1469-1480. DOI:10.1175/JAM2423.1 |
Hansen B, 2007. A fuzzy logic-based analog forecasting system for ceiling and visibility[J]. Wea Forecasting, 22(6): 1319-1330. DOI:10.1175/2007WAF2006017.1 |
Leipper D F, 1995. Fog forecasting objectively in the california coastal area using libs[J]. Wea Forecasting, 10(4): 741-762. DOI:10.1175/1520-0434(1995)010<0741:FFOITC>2.0.CO;2 |
Marzban C, Leyton S, Colman B, 2007. Ceiling and visibility forecasts via neural networks[J]. Wea Forecasting, 22(3): 466-479. DOI:10.1175/WAF994.1 |
Tudor M, 2010. Impact of horizontal diffusion, radiation and cloudiness parameterization schemes on fog forecasting in valleys[J]. Meteor Atmos Phy, 108(112): 57-70. |
 2017, Vol. 43
2017, Vol. 43 