引言

强对流天气局地性强、发展迅速，天气现象发展剧烈，伴随出现的冰雹、雷暴大风与短时强降水等天气，具有很强的致灾性。中央气象台定义的雷暴大风是指伴随强对流风暴出现的风速超过17.2 m·s^-1的大风天气。雷暴大风往往伴随飑线、阵风锋、龙卷等强对流天气而出现，风速大、发展迅速、突发性强，对生命财产安全造成极大威胁，因此对雷暴大风的监测与预报具有极其重要的意义。对雷暴大风进行实时、有效的监测是对其进行预报与研究的基础。然而，目前我国的气象监测体系中只包含温、压、湿、风等常规气象要素与闪电、降水等天气现象的观测，对于雷暴大风这样一个综合天气现象，并无特定的观测。

雷暴大风往往包括下击暴流大风、阵风锋大风等(郑永光等，2013)，其识别的难点在于如何将其与冷空气大风、台风大风、高山站大风、海岛站大风等非强对流大风区分开来。由于缺乏直接的监测数据，往往利用其他数据进行综合判断。2014年之前，将与雷暴、冰雹等强对流天气同时出现的大风视为雷暴大风记录(余蓉等，2012；郑永光等，2013)。国外也采用类似的方法，Lombardo et al(2009)利用极值分析法，结合雷暴人工观测，通过匹配大风与雷暴发生时间，区分雷暴大风与非雷暴大风。2014年之后，由于地面观测调整，取消了雷暴的人工观测(中国气象局综合观测司，2013)，使利用雷暴观测数据不再可行。

另一方面，利用天气雷达、卫星云图数据可对雷暴大风等天气现象进行一定识别(吴翠红等，2012；方翀等，2014)。王萍和牛智勇(2014)利用单站雷达数据，发现中层径向辐合(MARC)对雷暴大风、冰雹、短时强降水的识别具有较好的指示性。李国翠等(2013；2014)利用雷达三维组网数据，统计分析了对流性地面大风的6个雷达识别指标:最大反射率因子、最大垂直积分液态水含量、垂直积分液态水含量随时间变率、风暴最大反射率因子下降高度、风暴体移动速度和垂直积分液态水含量密度等参数，建立隶属函数和权重系数，建立了具有模糊逻辑的对流性地面大风识别方法。以上这些单纯基于雷达数据的雷暴大风识别方法，虽然在一定程度上能够实现对雷暴大风的区域性监测，但尚无法实现对雷暴大风的全国监测。

本文尝试在地面气象观测站大风观测记录的基础上，结合多源数据(包括温度、露点等地面气象站观测数据以及闪电、雷达、卫星等遥感数据)，利用模糊逻辑算法，建立一套全国范围的雷暴大风自动识别的算法，为我国强对流监测体系实现雷暴大风的实时监测。

1 数据与方法 1.1 质量控制数据

本算法使用的测风数据来自全国多要素(包括温、压、湿、风)自动气象站，全国约50000个站点。利用国家雷电监测网络的地闪定位数据、全国多普勒雷达基本反射率拼图数据、风云气象卫星的红外亮温等数据对雷暴大风进行识别。

雷暴大风与非雷暴大风训练样本数据使用来自国家气象信息中心提供的826个气象观测站(包括国家基准气候站、国家基本气象站)的“中国气候日值数据集”。该数据集能提供观测站点的人工天气现象观测数据，包括大风、雷暴、冰雹、龙卷等。用冰雹、雷暴、龙卷风等天气现象对大风数据进行识别，得到雷暴大风数据，其作为样本训练数据。具体方法为：对于出现大风的站点，如果大风记录前后1小时有雷暴、冰雹、龙卷等强对流天气现象记录，则认为是雷暴大风天气。

1.2 区域划分与季节划分

我国国土面积辽阔，各地气候各异，发生雷暴大风的条件具有较大差异。按照气候特征和便于统计分析原则，将我国大陆地区划分为7个区域：东北、西北、华北、华中、华南、西南和西藏(图 1)。

雷暴大风具有较强的季节性，一般而言，春季与夏季为雷暴大风的多发期，秋季发生频次急剧降低，冬季基本无雷暴大风的发生(孙继松等，2013)。为了进一步增加温度与露点对于雷暴大风的区分度，按照我国的气温与露点随月份的变化，本文对季节进行了划分，将4、5、6、7、8、9月划分为暖季，10、11、12、1、2、3月划分为冷季(张世轩等，2011)。本文分别统计暖季和冷季的隶属度函数，进行雷暴大风质量控制(以下简称质控)。

1.3 模糊逻辑算法

1965年，美国数学家Zadeh(1965；1975) 首先提出了模糊集合的概念，标志着模糊数学的诞生。模糊逻辑善于表达界限不清晰的定性知识与经验，借助隶属度函数概念，区分模糊集合，处理模糊关系，模拟人脑实施规则型推理，在气象、工程控制等领域有着广泛的应用(Cho et al, 2006；Gourley et al, 2007)。

由于雷暴大风出现的物理环境仍属于“模型未知”或“不能确定的描述系统”，无法设定精确的阈值判断其是否发生，此时运用“模糊逻辑”，可模仿人脑的方式，实现判断。本文应用模糊逻辑，对大风出现站点对应的温度、露点和周围闪电数量、雷达回波强度与卫星红外亮温等情况，根据大量数据的统计分布规律，确定各项质控物理量参数的质控权重，最终实现对雷暴大风与非雷暴大风的有效识别。

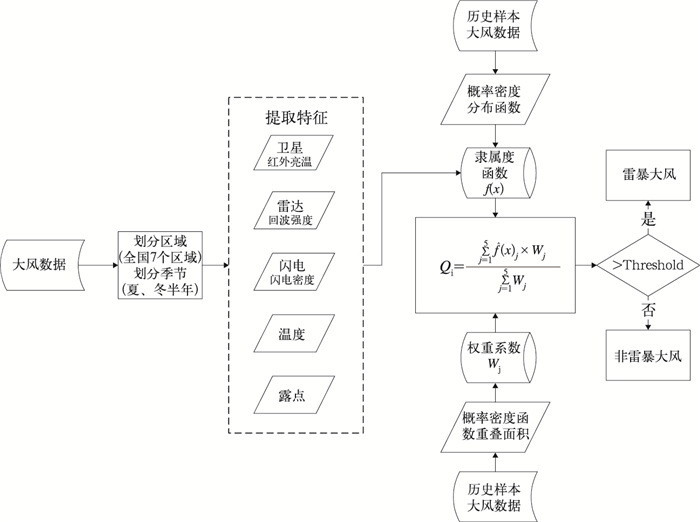
2 雷暴大风识别算法

算法具体流程(图 2)主要包括4步：

(1) 利用统计法得到隶属度函数与权重系数：本文使用2011—2013年的全国826个观测站171188个的大风观测记录提取雷暴大风与非雷暴大风的概率密度分布函数，计算得到隶属度函数与权重函数。

(2) 提取大风记录对应的各项特征参数，包括卫星云顶红外亮温、雷达回波强度、闪电密度、温度、露点等。

(3) 计算得到各项特征参数的隶属度与权重，计算得到概率Q。将第二步得到的各项特征参数代入隶属度函数，得到对应隶属度，综合隶属度与权重函数，即可计算雷暴大风概率Q。

(4) 通过对历史数据的分析，选取最优的概率阈值Threshold，用于区分雷暴大风与非雷暴大风。如果Q＞Threshold，则判定为雷暴大风；如果Q＜Threshold，则判定为非雷暴大风。

2.1 隶属度函数

隶属度函数的建立是模糊逻辑算法的基础。隶属度定义为若对论域(研究的范围)U中的任一元素x，都有一个数A(x)∈[0，1]与之对应，则称A为U上的模糊集，A(x)称为x对A的隶属度。隶属度函数的确立方法有模糊统计法、专家经验法以及例证法等(王季方和卢正鼎，2000)。本文采用模糊统计法，通过对特征进行大样本概率分布统计，得到隶属度函数。由于样本数量有限，概率密度函数分布不规则，为了得到其更好的概率分布特征，本文利用高斯核密度函数(Silverman，1986)进行平滑拟合，具体公式如下：

$ \mathit{\hat f}\left(\mathit{x} \right){\rm{ = }}\frac{1}{{\mathit{\sigma }\sqrt {{\rm{2 \mathsf{ \mathit{π}} }}} }}\sum\limits_{\mathit{i}{\rm{ = 1}}}^\mathit{n} {{{\rm{e}}^{{\rm{ - [}}\frac{1}{2}{{\left({\frac{{{\mathit{X}_\mathit{i}}{\rm{ - }}\mathit{x}}}{\mathit{\sigma }}} \right)}^{\rm{2}}}{\rm{]}}}}} $

(1)

式中，$ \mathit{\hat f}\left(\mathit{x} \right)$为概率密度函数，n为数据量，X_i为ith观测量，x为独立变量。σ为平滑因子，利用Silverman’s rule(Silverman，1986)，取σ=1.06SD·$ {\mathit{n}^{ - \frac{1}{5}}}$，其中SD为样本的标准方差。

得到其雷暴大风的概率分布函数F_TWi和非雷暴大风的概率分布函数F_NWi之后，可得到其隶属度函数MF_i：

$ \mathit{M}{\mathit{F}_\mathit{i}}{\rm{ = }}\frac{{{\mathit{F}_{\mathit{TWi}}}}}{{{\mathit{F}_{\mathit{TWi}}}{\rm{ + }}{\mathit{F}_{\mathit{NWi}}}}} $

(2)

隶属度函数生成之后，根据其分布特征，温度和露点采用了升半岭形分布(式3) 对其进行拟合：

$ \mathit{M}{\mathit{F}_\mathit{i}}{\rm{ = }}\left\{ \begin{array}{l} 0\\ \frac{1}{2} + \frac{1}{2}{\rm{sin}}\frac{{\rm{ \mathsf{ \mathit{π}} }}}{{\mathit{b}{\rm{ - }}\mathit{a}}}\\ 1 \end{array} \right.\begin{array}{*{20}{c}} {\mathit{x} \le \mathit{a}}\\ {\mathit{a} < \mathit{x} < \mathit{b}}\\ {\mathit{x} \ge \mathit{b}} \end{array} $

(3)

式中a、b为拟合参数。

2.1.1 雷达回波强度

多普勒天气雷达是监测对流系统的基本手段，强对流系统往往具有反射率大、对流云顶高度高、垂直液态水含量较大的特点(冯桂力等，2010；方翀等，2015)。大风地区的雷达回波特征，可判断大风是否为对流系统而产生。由于阵风锋等大风速区往往距离强对流主体存在一定的空间距离(徐芬等，2016)，因此本文算法中取大风记录点半径20 km之内的最大雷达回波参数。由于监测范围较大，因此本文工作中雷达数据使用的是中国气象局气象探测中心提供的全国雷达基本反射率拼图产品。

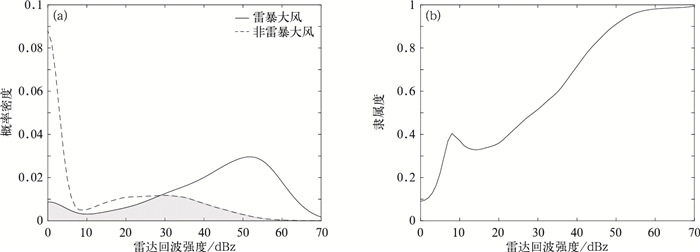
由图 3可见，雷达回波强度对两种大风的区分度较高。非雷暴大风的雷达回波主要分布在10 dBz以下，而雷暴大风则主要分布超过30 dBz，峰值分布于53 dBz，对应于雷暴大风较强的对流系统。隶属度函数显示，当雷达回波强度超过30 dBz，其为雷暴大风的概率达到50%，当雷达回波强度超过50 dBz，其隶属度超过90%；隶属度函数在10 dBz左右出现一个概率极大值，与对流初生、远离对流主体的阵风锋等环境，雷达回波较弱的情况下的对流性大风相对应。

2.1.2 闪电密度

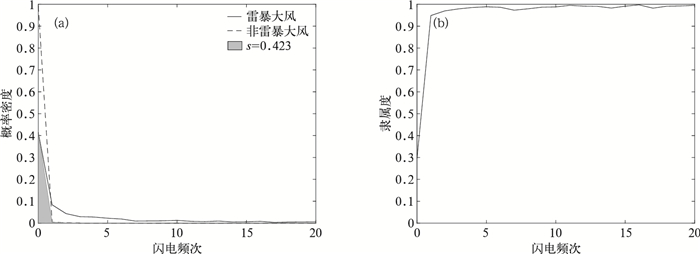
闪电是雷暴中的经常伴随的的天气现象(俞小鼎等，2005；郑媛媛等，2004)。雷暴大风必定伴随雷暴等对流系统出现，因此闪电是区分雷暴大风与非雷暴大风的关键因素。本文的统计，取大风记录点半径21 km(周康辉等，2014)的闪电数量，得到雷暴大风与非雷暴大风的闪电概率密度分布与隶属度函数(图 4)。

闪电对于雷暴大风的具有较好的区分性，其重叠面积s=0.423。从概率密度函数来看，超过60%的雷暴大风都伴随闪电现象；非雷暴大风的大风天气，也会出现伴随出现闪电的现象，但是其概率极低，累积概率低于3%。

由于以上原因，闪电的隶属度函数在质控过程中权重较大，可作为识别雷暴大风的重要参量。

2.1.3 红外亮温

风云气象卫星能实现全国范围的可见光云图、红外云顶亮温、水汽等气象要素观测。对于监测大范围的中尺度对流系统(mososcale convective system，MCS)具有独特的优势(郑永光等，2008)。利用大风记录点的云顶红外亮温，同样可有效判断该大风是否伴随强对流系统而出现(方翀等，2014；费海燕等，2016)。与雷达数据相似，算法中同样取大风记录点半径20 km之内的云顶红外亮温参数。

由图 5可见，红外亮温对于雷暴大风与非雷暴大风具有很好的区分性。雷暴大风的云顶红外亮温概率密度峰值出现在-50℃，而非雷暴大风的峰值出现在0℃左右。隶属度函数可见，若红外亮温低于-25℃，其为雷暴大风的概率超过50%；当红外亮温低于-50℃，其为雷暴大风概率超过70%。

2.1.4 地面温度

雷暴大风与非雷暴大风地面温度具有一定差异。冷空气大风出现在较强冷空气过程中，因此其地面温度往往较低。因此，温度可作为区分冷空气大风与雷暴大风的重要参量。

由于篇幅限制，无法给出全国每个区域的概率分布函数和隶属度函数，这里以西南和西北地区的情况为例(图 6)。由图 6可见：

(1) 西南地区冷季，雷暴大风最易出现的温度为15℃左右，非雷暴大风出现概率最高的温度为0℃左右。冷季，两者重叠面积为0.587，具有一定的区分度；暖季，雷暴大风与非雷暴大风出现概率最高的温度均在25℃左右，两者重叠面积达到0.837，温度对于两者的区分度明显较冬季更低。

(2) 西北地区冷季雷暴大风出现概率最高的温度为9℃，非雷暴大风为-2℃，两者区分度为0.479；暖季，区分度下降至0.887，雷暴大风与非雷暴大风最易出现的温度均在25℃左右。

由此可见，不同地区、不同季节，温度对于雷暴大风与非雷暴大风的区分度具有较大差异。冬季，雷暴大风发生的温度明显偏高，夏季则与非雷暴大风差异较小；同样的温度，西南地区与西北地区发生雷暴大风的概率也有显著的差异。由此可见，对于全国分区、分季节处理，是很有必要的。

2.1.5 地面露点

地面露点是表征地面湿度的重要参量。露点越高，地面水汽含量越大。雷暴大风发生的环境特征需要一定的水汽条件(王秀明等，2013；钟利华等，2011)，因此，露点可以作为雷暴大风识别的重要参数。

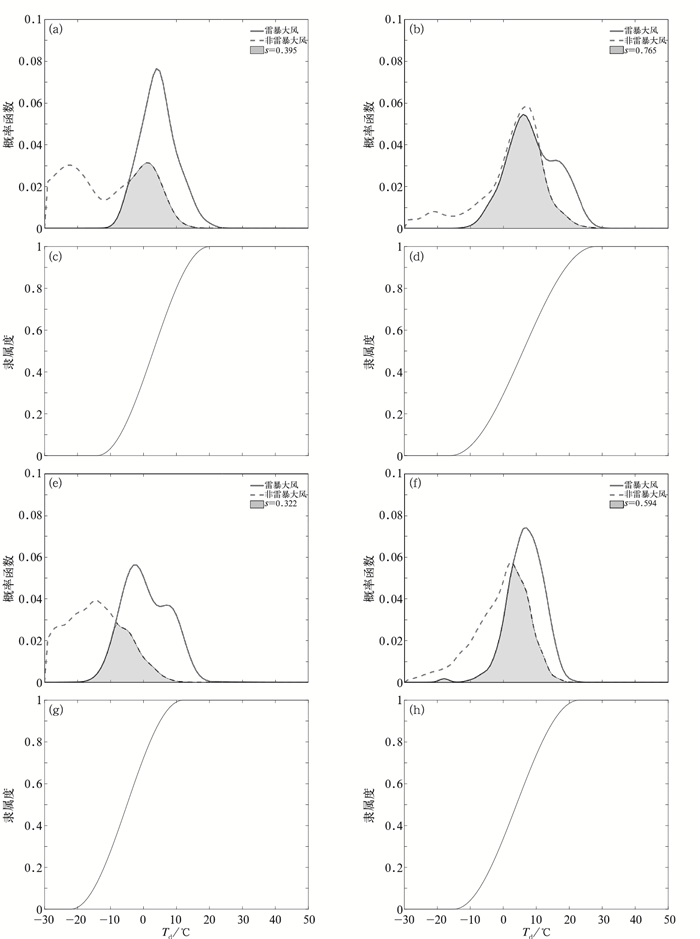
图 7可见，露点温度相对于温度具有更好的区分性：

(1) 冷季，西南地区雷暴大风的概率最大值出现在露点为5℃，非雷暴大风则在露点为-20℃和2℃呈现双峰结构，两者重叠面积仅为0.395；暖季，西南地区雷暴大风与非雷暴大风的最大概率均出现在露点为8℃左右，重叠面积达到0.765，区分性较差。

(2) 西北地区情况与西南地区类似，但是露点呈现出更好地区分布；冷季，雷暴大风最易出现在露点为-1℃的情况，而非雷暴大风最易出现在-15℃，概率密度曲线重叠面积为0.322；暖季，雷暴大风与非雷暴大风的露点区分度变差，重叠面积为0.594。

西北地区与西南地区露点温度的差异与气候分布一致。雷暴大风一般发生于强对流环境之中，因此必须具备一定的湿度条件，要求露点温度较高；非雷暴大风，如冷空气大风，则一般发生在较干冷的环境场中。这一差异在冷季显得更为明显。

2.2 权重

对于参与统计识别的物理量，包括温度、露点、闪电密度、雷达回波强度、云顶红外亮温，每个物理量对于雷暴大风的区分度有所差异，比如闪电对雷暴大风具有较高的区分度，当出现闪电的时候，大风记录为雷暴大风的记录超过60%。相对而言，露点和温度的区分度相对较差。因此，需要确定各个物理量在质量控制中的权重W，参照Gourley et al(2007)的方法，其计算公式如下：

$ {\mathit{M}_\mathit{j}} = \frac{1}{{{\mathit{A}_\mathit{j}}}}\sum\limits_{\mathit{j} = 1}^5 {\frac{1}{{{\mathit{A}_\mathit{j}}}}} $

(4)

式中，A_j为雷暴大风与非雷暴大风的概率密度分布函数的重叠面积(如图 3~7中的阴影部分)。若A越小，该参数对与雷暴大风与非雷暴大风的区分度就越佳，其参与质控的比重就越大；反之，则参与质控的比重就越小。

表 1为西北地区与西南地区各项物理量参与质控的权重分布情况。可以看到，冷季与暖季具有较大差异。冷季，西北地区露点与温度的质控权重较大，分别达到25.69%与17.27%；暖季，其权重下降，分别为17.35%与11.61%。雷达、闪电、卫星数据的权重系数在暖季高于冷季，其中雷达的权重系数最大，其次为闪电。西南地区情况类似，温度与露点权重相对较低，雷达、卫星、闪电数据权重相对较高。

2.3 模糊解码

确定了各个物理量的权重系数之后，则可计算得到总的概率系数Q：

$ {\mathit{Q}_\mathit{i}} = \frac{{\sum\limits_{\mathit{j} = 1}^5 {\mathit{\hat f}{{\left(\mathit{x} \right)}_\mathit{j}} \times {\mathit{W}_\mathit{j}}} }}{{\sum\limits_{\mathit{j} = 1}^5 {{\mathit{W}_\mathit{j}}} }} $

(5)

式中，W_j为权重系数，$ {\mathit{\hat f}{{\left(\mathit{x} \right)}_\mathit{j}}}$为隶属度。

2.4 模糊阈值的确定

通过隶属度与权重函数等计算流程后，最终得到概率Q，如何通过Q判断雷暴大风与非雷暴大风，这里通过选取阈值Threshold进行判断。

首先，引入识别正确率(POD)、误识别率(FAR)、临界成功指数(CSI)等参数，其定义如下：

$ \mathit{POD}{\rm{ = }}\frac{\mathit{h}}{{\mathit{h}{\rm{ + }}\mathit{m}}} $

(6)

$ \mathit{FAR}{\rm{ = }}\frac{\mathit{f}}{{\mathit{h}{\rm{ + }}\mathit{f}}} $

(7)

$ \mathit{CSI}{\rm{ = }}\frac{\mathit{h}}{{\mathit{h}{\rm{ + }}\mathit{m + f}}} $

(8)

式中，h为正确识别的数量，f为误识别为雷暴大风数量，m为雷暴大风漏识别数量。

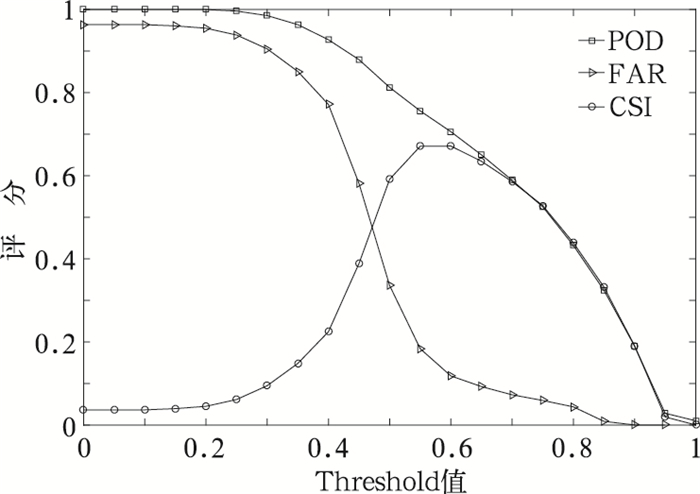
图 8给出了2010年共50873个大风样本在不同阈值情况下的POD、FAR、CSI等参数的分布情况。随着Threshold值的增大，POD值呈现出递减的趋势，正确识别数量减小，漏识别数量增多；FAR值同样呈现降低的趋势，因为随着Threshold的增大，被错误识别为雷暴大风的大风数量降低；CSI呈现出先增加后降低的趋势，在Threshold=0.55~0.6时达到最大值0.67，此时雷暴大风识别准确率约为0.76，误识别率约为0.18。

由此可见，Threshold值的选取对于雷暴大风的识别至关重要，若太高，则会导致雷暴大风漏识别的情况太多；若太低，则导致误识别率过高。实际工作中，可灵活选取。

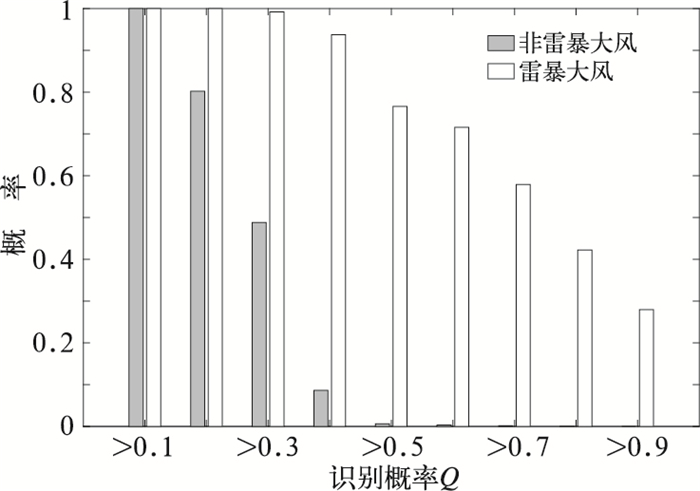
3 识别结果检验 3.1 检验统计结果

2010年共50873个大风样本，图 9给出了识别概率Q的分布情况。由图 9可见，雷暴大风与非雷暴大风的识别概率具有非常明显差别。超过93%的雷暴大风的Q值超过0.4，约78%的雷暴大风的Q值超过0.5；与此相对应，约91%的非雷暴大风识别概率低于0.4，非雷暴大风的Q超过0.5的比例急剧降低，低于1%。若Threshold=0.42，算法能识别92%的雷暴大风，同时能识别93%非雷暴大风；若Threshold=0.55，识别到的雷暴大风比例降至76%，但是非雷暴大风识别率上升至99%。

3.2 天气过程识别检验

为了验证上述方法的效果，本节选取了2013年5月18日16:10与8月13日14:50两次大风过程。其中，2013年5月18日大风过程发生在内蒙古、陕西等地，大风过程以冷空气大风为主，夹杂着强对流天气大风。人工观测记录到大风10站次，其中非雷暴大风8站次，雷暴大风2站次。2013年8月13日大风过程属于热带气旋外围的大风。

从雷达拼图(图 10a)与卫星云图(图 10b)可以看到，2013年5月18日，冷空气南下，在冷空气前沿，触发东北—西南向狭长的强对流。非雷暴大风主要发生于以红外亮温暗区为特征的冷空气后部；雷暴大风发生于对流系统附近，对流系统周围存在较弱的闪电活动，探测到为数不多的地闪(图 10a)。2013年8月13日的大风过程属于台风尤特外围云系触发一系列强对流系统，引发雷暴大风；同时，台风导致的非对流性大风与雷暴大风同时存在。

利用模糊逻辑算法，其各项特征量与识别情况如表 2。由表 2中可以看到，2013年5月18日16:10过程温度露点差较大、大气环境较干，属于典型的冷空气南下大风过程。相对而言，非雷暴大风的露点更低，T-T_d较大，空气层结较干；雷暴大风周围存在对流系统的发生发展，因此其雷达回波强度与红外亮温均显示着对流云的存在，而非雷暴大风对应冷空气大风，底层雷达探测回波反射率为0，卫星探测显示高空存在一定的高层云系；非雷暴大风站点附近均无闪电发生，雷暴大风站点中有1个站点周围探测到1个闪电。

2013年8月13日14:50，各大风记录的温度和露点较为接近，但是其他3个参数具有较大差异。非雷暴大风周围均未探测到闪电，同时距离对流云存在一定距离，雷达回波为0，红外亮温较高，Q值均在0.5以下。相对而言，雷暴大风记录周围均探测到比较明显的对流活动，Q值均超过0.7。

总体而言，可以看到选取个例中Q具有较好的区分性，若Threshold选取为0.55，能较好地实现雷暴大风与非雷暴大风的分类。

4 结论与讨论

本文在地面观测站大风记录的基础上，结合多源数据，包括雷达、卫星、闪电、温度、露点等观测数据，利用模糊逻辑算法，实现了对雷暴大风与非雷暴大风的有效识别。算法利用统计方法得到2011—2013年多源数据的概率分布函数，进而计算得到其隶属度函数。采用概率重叠面积方法，确定各项质控数据的权重，最后通过选取概率阈值的方法，实现对雷暴大风的识别。

通过对2010年50873条人工观测历史数据的识别结果检验表明，该算法能有效区分雷暴大风与非雷暴大风，当判断阈值选取0.55时，对于雷暴大风的识别正确率POD约为0.76，误识别率约为0.18，CSI指数约为0.67，对于非雷暴大风POD约为0.99，对于强对流监测业务应用具有一定的参考意义。文中选取了两次大风过程，算法正确地识别了11个非雷暴大风记录，5个雷暴大风记录，表现出一定的实用性。

在强对流监测中，雷暴大风由于其局地性与强致灾性一直是监测的难点与重点。本文使用模糊逻辑算法，建立了较为科学合理的识别模型，实现了雷暴大风与非雷暴大风的区分，为强对流监测引入了新的思路。算法具有较好的兼容性，后续工作可以尝试将更多的数据加入质控数据源，并将其用于短时强降水与冰雹等强对流监测数据的质控，建立科学合理的强对流监测体系。