引 言

黑潮(Kuroshio)是沿着北太平洋西部边缘向北流动的一支强西边界海流，它具有高温、高盐、流量大、流速强、厚度大、流幅窄等特征(Nitani, 1972; Su et al, 1990; Bryden et al, 1991)。黑潮的主干经吐噶喇海峡，进入太平洋后，沿日本列岛南部海区向东的海流被称为黑潮延伸体(Kuroshio Extension)(Qiu, 2003)。在冬季，黑潮延伸体区域因温度比较高而释放巨大的热量加热大气，是全球气候系统热量经向输送的关键海区之一，在全球气候变化中起着非常重要的作用。黑潮延伸体是黑潮与亲潮相交汇的区域，高温的黑潮与低温的亲潮相汇形成明显的海洋温度锋区，海洋锋的作用使该区域成为中纬度海洋大气相互作用的关键区域(Barnett et al, 1999; Wallace and Hobbs, 2006)。

大气风暴轴一般是指大气中2.5~6 d瞬时扰动最活跃的区域(Blackman, 1976；1977)，代表了大气中天气尺度系统(风暴)的重要活动特征，风暴在大气系统中起到了重新分配热量和能量的作用，从而有利于维持大气中温度、能量、湿度以及其他基本因子的平衡(Held et al, 1989)；同时，风暴的活动也是中纬度地区海洋大气能量相互交换的一种重要途径。黑潮延伸体区域海洋锋区与北太平洋风暴轴在位置上有很好的对应关系(任雪娟等, 2007)，该区域是激发大气中天气尺度系统活动的重要区域。Hoskins and Valdes(1990)利用一个定长波模型证明了非绝热加热对维持中纬度西边界流上空的最大平均斜压性具有重要作用，它可以抵消增长性斜压涡旋对经向温度梯度和低层斜压性的减弱效应。Nakamura et al(2004)进一步提出一种可能的机制，认为穿越强SST梯度的不同感热加热增强了低层大气狭窄区域的斜压性并锚定了其上空的风暴轴。有学者利用区域大气数值模式研究指出风暴轴的强度和结构受中纬度地区增强的SST梯度影响很大，其所处纬度位置对海洋温度锋也很敏感(Chen et al, 2010; Ogawa et al, 2012)。Joyce et al(2009)发现近表层的天气尺度扰动的年际变率与黑潮延伸体区域海表温度锋(定义为200 m深度14℃等温线的第一主分量)弱的经向位移存在显著但并不完全一致的关系。冯劭华等(2015)发现黑潮延伸体区域中尺度涡活动强度和位置的变化对应着北太平洋风暴轴强度和位置的变化。O'Reilly and Czaja(2015)指出海表温度锋强度较强(弱)时，西太平洋区域北太平洋风暴轴增强(减弱)，而东太平洋区域北太平洋风暴轴减弱(增强)。袁超和徐海明(2016)指出北太平洋风暴轴的强度和位置变化与北太平洋海温异常存在很好的相关性。

1 资料和方法 1.1 资料

海表温度数据来自美国国家海洋大气局(National Oceanic and Atmospheric Administration, NOAA)的逐日最优插值SST(optimum interpolation sea surface temperature, OISST)资料，空间分辨率为0.25°×0.25°，时间段为1981年9月1日至2015年2月28日。

大气数据来自美国国家环境预报中心(National Center for Environmental Prediction, NCEP)和美国国家大气科学研究中心(National Center for Atmospheric Research, NCAR)的全球大气逐日再分析资料。本文主要使用850 hPa的经向风场、纬向风场和温度场等，水平分辨率为2.5°×2.5°，时间段为1981年9月1日至2015年2月28日。

1.2 黑潮延伸体区域海表温度锋强度和位置的确定方法

为了与北侧的亲潮延伸体海表温度锋区别开来，将研究区域选在33°~39°N、140°~154°E，计算黑潮延伸体区域海表温度锋强度和位置指数的具体步骤为：

首先计算研究区域范围内的SST水平梯度 $\left| {\nabla \mathit{\boldsymbol{T}}} \right|$

$\left| {\nabla \mathit{\boldsymbol{T}}} \right| = \sqrt {{{\left( {\frac{{\partial T}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial T}}{{\partial y}}} \right)}^2}} $

(1)

式中T为SST。

然后，用研究区域内每一经度值上SST水平梯度最大值的点表征黑潮延伸体区域海表温度锋，用此SST水平梯度最大值来表征海表温度锋的强度，用SST水平梯度最大值所在纬度表征海表温度锋的位置。

1.3 北太平洋风暴轴的表示

位势高度方差、扰动动能和经向输送热通量这三个物理量的中心大小和位置均可以反映出风暴轴的强弱和位置(傅刚等，2009)，本文选用经向输送扰动热通量v′T′(v为经向风速，T为大气温度)表征北太平洋风暴轴，利用朱伟军和孙照渤(2000)介绍的31点带通滤波器从逐日资料v和T中提取出天气尺度(2.5~6 d)振荡分量，计算得到经向输送扰动热通量v′T′。

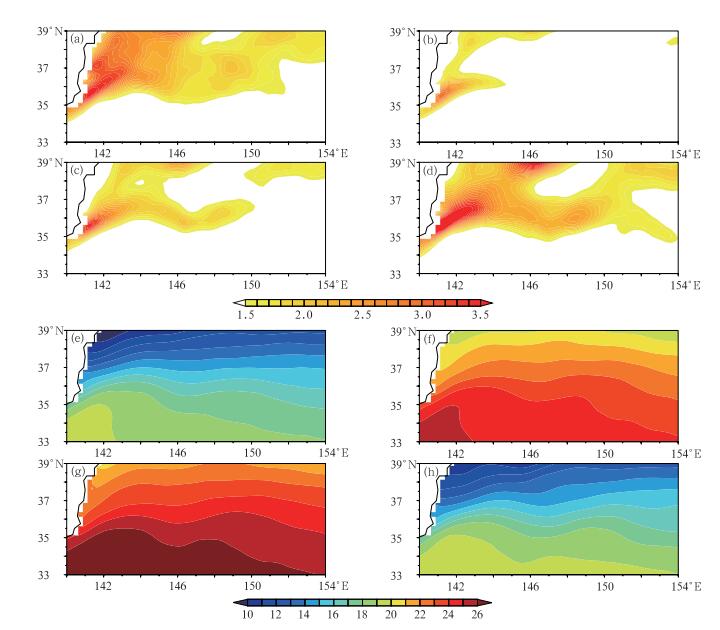
2 黑潮延伸体区域海表温度锋季节变化对北太平洋风暴轴的影响 2.1 黑潮延伸体区域海表温度锋的季节变化

图 1a~1d分别给出的是春季、夏季、秋季以及冬季黑潮延伸体区域SST水平梯度分布，图 1e~1h给出的分别是相对应的SST分布，从图中可以看出，春季SST较低，但在黑潮延伸体区域北部边缘等温线较密集且平直，导致海表温度锋的强度较强，锋区南北跨度大，弯曲程度小，较为平直。夏季虽然SST较高，但等温线非常稀疏，海表温度锋仅在上游比较明显，而在下游由于南北海温差异不显著，因此海表温度锋几近消失。进入秋季，SST达到最高，等温线逐渐变得密集且出现明显弯曲，海表温度锋的强度明显增强，且锋区南北较狭窄。冬季SST显著降低，但等温线却变得最为密集且出现非常显著的弯曲，海表温度锋的强度达到最强。

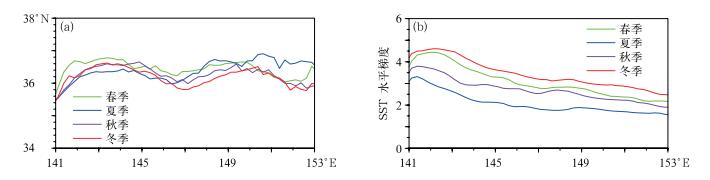
图 2a和2b分别给出的是根据1.2节中介绍的方法确定的黑潮延伸体区域海表温度锋位置和强度的季节变化，与图 1a~1d给出的不同季节的海表温度锋相比，可以看出本文使用的方法也能很好地反映海表温度锋的季节变化特征。从图 2a中可以看出黑潮延伸体区域海表温度锋南、北位置的季节变化很弱，春季海表温度锋稍偏北，秋季和冬季居中，夏季上游海表温度锋锋区位置偏南，而下游位置又偏北。相比较而言，图 2b给出的黑潮延伸体区域海表温度锋强度的季节变化则非常显著，冬季最强，在141°~153°E范围内强度的平均值为3.45 ℃·(100 km)^-1，其次为春季，强度的平均值为3.08 ℃·(100 km)^-1；其次为秋季，强度的平均值为2.71 ℃·(100 km)^-1；夏季最弱，强度的平均值为2.09 ℃·(100 km)^-1。

2.2 北太平洋风暴轴对黑潮延伸体区域海表温度锋季节变化的响应

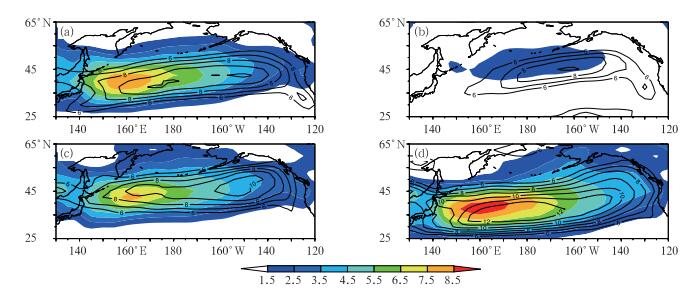
图 3a~3d分别给出的是春季、夏季、秋季以及冬季850 hPa北太平洋风暴轴的分布，图中风暴轴的形态与急流的分布非常相似。春季、秋季以及冬季风暴轴的强度中心位于上游，这是由于在黑潮延伸体区域海表温度锋区，较强的海温梯度维持了上空较强的大气斜压性，使得斜压涡旋在那里不断生成及活动，其天气尺度涡旋随风向下游运动，引起热量的向极输送；同时，由于运动中的斜压涡旋强度不断减弱，风暴轴的强度中心位于上游，但由于夏季黑潮延伸体区域南北海温差异较小，海表温度锋强度非常弱，因此风暴轴的强度中心位于北太平洋中部地区。对不同季节的风暴轴进行对比可以发现，冬季北太平洋风暴轴位置偏南，强度最强，而夏季位置偏北，且强度最弱，春季和秋季为过渡阶段。对比图 2给出的不同季节海表温度锋位置和强度的变化可以看出，北太平洋风暴轴强度与海表温度锋强度具有一致的协同变化，而由于海表温度锋位置的季节变化很弱，因此北太平洋风暴轴的变化主要是对海表温度锋强度季节变化的响应。

Hoskins and Valdes(1990)强调了大气斜压不稳定性增长率是斜压波(风暴轴)成长至关重要的因素，其为风暴轴的发展提供了斜压能量。本文计算了大气斜压不稳定性增长率

$\sigma =0.31f\left| \frac{\partial V}{\partial Z} \right|{{N}^{-1}}$

(2)

式中, f为科氏参数，V为风速，N为Brunt Vaisala频率(Lindzen and Farrell, 1980)，根据其大小来判断北太平洋风暴轴的发展。一般来说σ越大，斜压性越强，有利于风暴轴的发展，反之亦然。

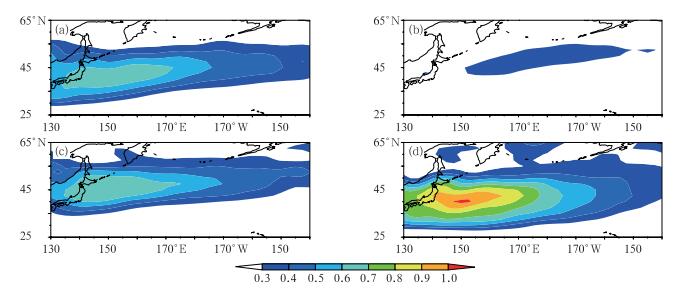
图 4a~4d分别给出的是春季、夏季、秋季以及冬季850 hPa大气斜压不稳定增长率的分布，对比图 3可以看出，斜压不稳定增长率与风暴轴的分布具有相当好的一致性。冬季海表温度锋强度最强，使大气南北温度梯度增大，增强了其上空大气的斜压性，斜压涡旋活动更加频繁，因此北太平洋风暴轴强度在西太平洋海域显著增强，尤其是黑潮延伸体区域，且其中心轴线位置偏南；而夏季海表温度锋非常弱，黑潮延伸体区域的大气斜压性显著减弱，导致斜压涡旋活动在此减弱，而主要在太平洋中部海域生成，北太平洋风暴轴强度中心移到太平洋中部区域，且位置偏北。春季和秋季的大气斜压稳定率分布均表现为过渡阶段的特征。

此外，考虑到影响涡旋利用时间平均流斜压性的效率不仅取决于大气斜压不稳定性增长率，其影响因素还有很多(Chang, 2001)，因此诊断分析局地斜压能量转换(baroclinic energy conversion，BCEC)很有必要。参照Cai et al(2007)的研究，从平均有效位能(mean available potential energy，MAPE)向涡动有效位能(eddy available potential energy，EAPE)的斜压能量转换为：

${\rm{BCEC}}1\left( {{\rm{MAPE}} \to {\rm{EAPE}}} \right) = - {C_1}{\left( {\frac{{{p_0}}}{p}} \right)^{\frac{{R}}{{^{{c_p}}}}}}{\left( { - \frac{{{\rm{d}}\theta }}{{{\rm{d}}p}}} \right)^{ - 1}}\left( {\overline {u'T'} \frac{{\partial \overline T }}{{\partial x}} + \overline {v'T'} \frac{{\partial \overline T }}{{\partial y}}} \right)$

(3)

从EAPE向涡动动能(eddy kinetic energy，EKE)的斜压能量转换为：

${\rm{BCEC}}2\left( {{\rm{EAPE}} \to {\rm{EKE}}} \right) = - {C_1}\left( {\overline {\omega 'T'} } \right)$

(4)

式中， ${C_1} = {\left( {\frac{{{p_0}}}{p}} \right)^{\left( {\frac{{{c_v}}}{{{c_p}}}} \right)}}\left( {\frac{R}{g}} \right)$ ，R，ω，θ，c_p(c_v)分别为干空气气体常数、垂直速度、位温、干空气的比定压热容(干空气的比定容热容)。MAPE，EAPE，EKE这三个物理量在前人的研究中被广泛应用于风暴轴变率以及全球变暖变化方面的研究(Yin, 2005; Mizuta et al, 2011; Wu et al, 2011)。

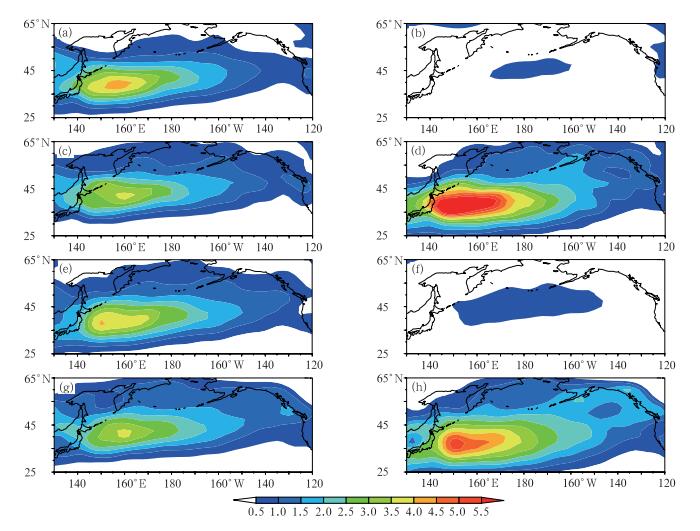
图 5a~5d分别给出的是春季、夏季、秋季以及冬季850 hPa斜压能量转换的分布，冬季从平均有效位能向涡动有效位能的斜压能量转换(BCEC1) 以及从涡动有效位能向涡动动能(BCEC2) 的斜压能量转换均在黑潮延伸体区域显著增强，而在夏季斜压能量转换则显著减弱，且中心移到太平洋中部，位置偏北。春季和秋季为过渡阶段，且春季的斜压能量转换在黑潮延伸体区域略强于秋季，这些均与图 3给出的风暴轴的季节分布具有相当好的一致性。

3 结论与讨论

本文利用NOAA最优插值逐日SST数据分析了黑潮延伸体区域海表温度锋的季节变化，并分析了其对北太平洋风暴轴的影响，结合对大气斜压性不稳定增长率以及局地斜压能量转化的分析，得到主要结论如下：

黑潮延伸体区域海表温度锋南北位置的季节变化很弱，春季海表温度锋稍偏北，秋季和冬季居中，夏季上游海表温度锋锋区位置偏南，而下游位置又偏北，其强度的季节变化则非常显著，冬季最强，其次为春季、秋季，夏季最弱。

黑潮延伸体区域海表温度锋的季节变化对北太平洋风暴轴具有显著的影响，且由于海表温度锋位置的季节变化很弱，北太平洋风暴轴的变化主要是对海表温度锋强度季节变化的响应。北太平洋风暴轴在冬季最强，其次为春季、秋季，夏季最弱，这种强度的季节变化与海表温度锋强度的季节变化是一致的。在冬季，北太平洋风暴轴位置偏南，而在夏季偏北，春季和秋季居中，这表明海表温度锋区强的海温水平梯度可以将大气中的风暴轴锚定在其上空。

冬季黑潮延伸体区域海表温度锋强度最强，增强了其上空大气的斜压性，从平均有效位能向涡动有效位能的斜压能量转换以及从涡动有效位能向涡动动能的斜压能量转换均在黑潮延伸体区域显著增强，斜压涡旋在此区域生成更加频繁，在随西风向下游运动过程中不断从背景平均流中获得能量，从而导致北太平洋风暴轴增强，且固定在黑潮延伸体区域上空，而夏季黑潮延伸体区域海表温度锋强度非常弱，其上空大气斜压性减弱，从平均有效位能向涡动有效位能的斜压能量转换以及从涡动有效位能向涡动动能的斜压能量转换均显著减弱，斜压涡旋在此区域生成减少，导致北太平洋风暴轴减弱，且中心位于太平洋中部，位置偏北。

本文研究分析了黑潮延伸体区域海表温度锋的季节变化及其对北太平洋风暴轴的影响，并初步探讨了其可能的机制，由于中纬度海气相互作用的复杂性，其完整的物理机制还需要进一步的研究。