引言

相对湿度是描述空气中的水汽含量和潮湿程度的物理量，是全球观测系统(GCOS)重要组成，是气候变化监测中最重要的气象要素之一。相对湿度也是我国气象台站必须进行系统的、连续的观测项目之一。相对湿度的高低对春季低温阴雨、夏季闷热程度、冬季低温寒潮的发生和判定影响较大，是受社会关注度日益增加的“雾”和“霾”的重要判别指标。

均一性的长序列资料是进行气候研究的基础。Gaffend and Ross(1999)，Robinson(2000)，Brown and Degaetano(2013)分别对美国台站露点温度序列进行了均一性研究；Vincent et al(2007)对加拿大75个台站相对湿度进行了均一化分析。自2000年开始，我国相对湿度观测逐步由人工观测转为自动观测，至2014年已全部实现自动观测。自动气象站的观测原理、观测方法与人工观测相比发生了很大变化(茆佳佳等，2016; 任芝花等，2015)。气象台站个数也由新中国成立初期的200个左右发展到2400余个。因此，观测方式的转变、空间分辨率的提高、观测仪器升级等原因正是造成气候序列非均一的主要因素。Kaiser(2000)，Wang and Gaffen(2000)采用不同的方法分别对中国区域相对湿度序列进行了非均一性检验与订正，但观测台站密度较低。我国共建设2400余个国家级气象观测台站，近年来，基于对2400余个国家级地面站基础气象资料的质量检测、控制和更正，形成了一套长序列、高质量的数据产品——《中国国家级地面气象站基本气象要素月值数据集(Ⅴ3.0)》。利用此高质量的台站观测数据集，朱亚妮等(2015)利用加拿大环境部气候研究中心研发的PMTred和PMFT方法，对中国区域2400余个站相对湿度序列进行了非均一性订正，研制完成《中国国家级地面气象站均一化相对湿度数据集(Ⅴ1.0)》。

把离散的气象台站资料通过合适的空间内插方法转变成规则的格点数据，对于气候变化分析和数值模拟研究具有举足轻重的意义。在流域水文、精细农业、生态系统研究等方面也有着广泛的应用前景。Willett et al(2008)研制了第一个全球范围的均一化相对湿度格点数据集。但针对中国区域而言，采用的台站只有200个左右，资料的准确性和代表性存在一定的问题。空间网格数据精度不仅依赖插值方法，更与观测站密度密切相关。目前，国内外已经开展了一些包括降水(沈艳等，2010；赵煜飞等，2011；王杰等，2016)、气温(李庆祥等，2007；张强等，2009)、水汽压(沈艳等，2008)等的网格化工作，但是针对中国高密度台站均一化相对湿度网格化的研究较少。因此，亟需建立一个中国大陆范围、时间序列较为完整、准确性较高的地面均一化相对湿度格点数据集。

本文在《中国国家级地面气象站均一化相对湿度数据集(Ⅴ1.0)》的基础上，利用薄盘样条法，同时引入数字高程资料以尽可能地消除中国区域独特地形条件下高程对空间插值精度的影响，建立了1951年以来中国区域均一化相对湿度月值0.5°×0.5°格点数据集。为精确描述中国区域湿度时空变化特征、趋势分析等提供了数据基础。以下将主要针对相对湿度格点月值数据集(简称CR数据集)的建立及精度进行评估分析。

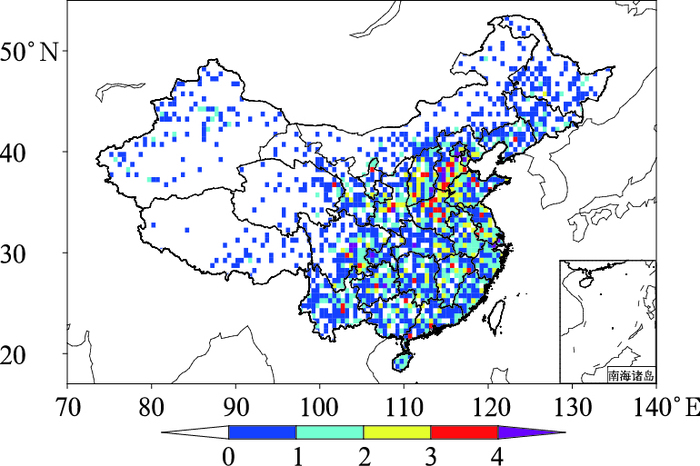
1 资料与方法 1.1 资料

用于空间插值的基础数据来源包括两个部分：(1)1951—2014年2413个国家级台站均一化逐月相对湿度资料。该资料是在各省、市、自治区气候资料处理部门逐月上报的《地面气象记录月报表》信息化资料基础上，经由国家气象信息中心收集、整理、检查、审核而成。采用PMTred和PMFT方法，选取均一的邻近站作为参考站，使用相关系数权重平均构建参考序列，结合元数据信息，研制完成《中国国家级地面气象站均一化相对湿度数据集(Ⅴ1.0)》。从1951—2014年站点数变化曲线(图略)可知，建站初期我国只有不足200个台站，1961年以后台站总数超过2000个且趋于稳定。图 1给出了2014年全国单位网格内站点数空间分布，可见，全国绝大部分地区单位网格内站点数均大于等于1，我国东南部地区单位网格内站数较多。另外，考虑到台站密度对插值的影响，基础数据源中不包括两个远海海岛站(西沙和珊瑚岛)。(2) 为了尽量消除中国独特地形条件下高程对相对湿度空间插值精度的影响，利用GTOP030数据(分辨率为30″×30″)重采样生成的中国范围0.5°×0.5°数字高程模型数据DEM(每个网格内地形曲面的平均海拔高度值)。

1.2 格点化方法

近年来，由于薄盘样条法(thin plate spline，TPS)只将空间分布作为观测数据的函数而不需要其先验知识和物理过程，并且插值的准确性较高(Hutchinson and Gessler, 1994；Hutchinson, 1995)，被广泛应用到气象要素的栅格化处理中(赵煜飞等，2014)。TPS可以被视作标准多变量线性回归的归纳或一般化，局部薄盘光滑样条(partial thin platesmoothing splines)是对薄盘光滑样条原型的扩展，它允许引入线性协变量子模型(刘志红等，2008)，以满足不同气象要素的插值需要。另外，ANUSPLIN软件是采用TPS进行转换分析和对多种变量进行栅格化的工具，使得TPS更加容易得以使用，软件中提供了GCV(generalized cross validation)和GML两种选择平滑参数的判断方法。

本文共设计了4组插值模型(表 1)，并根据广义交叉验证GCV的最小化确定了自变量为3个、高程数据DEM作为协变量、样条次数为3次的插值方案。对2400站相对湿度进行曲面拟合的过程，是把不同经纬度、海拔高度的相对湿度值，以误差最小的标准，光滑订正到固定经纬度以及固定经纬度对应的平均海拔高度的“盒子(0.5°×0.5°)”中来。

1.3 检验方法及评估指标

样条函数法实际上是采用M次多项式对采样曲线进行分段修匀，其拟合过程相当于用灵曲板来绘制分选连续的曲线。TPS是对样条函数法的曲面扩展，利用光滑参数来达到数据逼真度和拟合曲面光滑度之间的优化平衡。所以与基于统计插值技术Kriging等方法不同，TPS方法插值结果(采用ANUSPLIN软件)中不仅包括空间内插后的格点值，还同时计算出原始序列(台站实测值)的曲面拟合值(分析值)，便于直接计算插值过程造成的误差。

为了检验评估效果，本文选取分析值与台站原始实测值之间的偏差(MBE)、相对误差(RBE)、均方根误差(RMSE)、广义交叉验证平方根(RTGCV)以及相关系数(R)作为评估插值效果的指标。具体计算公式如下：

$RTGCV = \sqrt {GCV} $

(1)

$MBE = \frac{1}{N}\sum\limits_{i = 1}^N {({P_i} - {O_i})} $

(2)

$RBE = \frac{1}{N}\sum\limits_{i = 1}^N {(\frac{{{P_i} - {O_i}}}{{{O_i}}})} \times 100\% ,\;({O_i} \ne 0)$

(3)

$RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{(\frac{{{P_i} - {O_i}}}{{{O_i}}})}^2}} } $

(4)

$R = \frac{{\sum\limits_i^N {{P_i}{O_i}} - \frac{1}{N}\sum\limits_i^N {{P_i}} \sum\limits_i^N {{O_i}} }}{{\sqrt {\left( {\sum\limits_{i = 1}^N {P_i^2} - \frac{{{{(\sum\limits_{i = 1}^N {{P_i}} )}^2}}}{N}} \right)\left( {\sum\limits_{i = 1}^N {O_i^2} - \frac{{{{(\sum\limits_{i = 1}^N {{O_i}} )}^2}}}{N}} \right)} }}$

(5)

式(2)~式(5) 中，P_i为第i点上网格化分析值，O_i为台站实测值，N为样本总数。

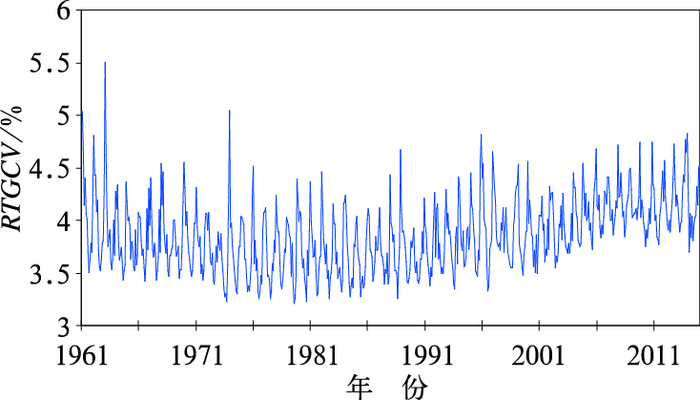
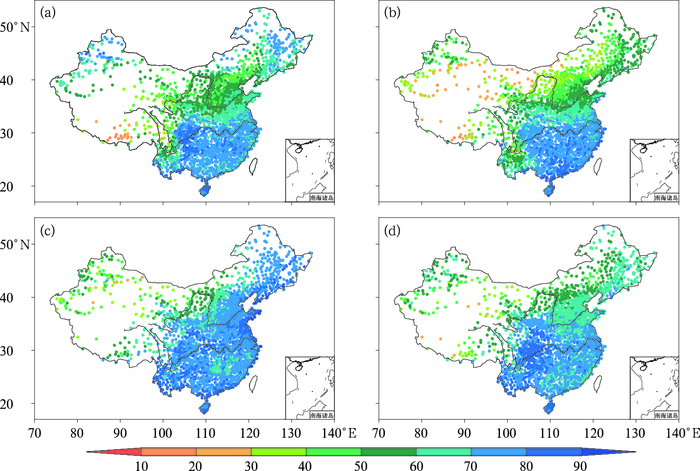
2 数据集质量评估 2.1 广义交叉验证

为了检验插值方法和插值模型对实际相对湿度场的插值效果，采用广义交叉验证的方法进行评估。其原理是首先假设每个站点的气象要素值未知，用周围站点的值来估算，然后根据所有站点实测值与估算值的误差大小评判插值方法的优劣。广义交叉验证误差GCV由输入数据误差和预计误差组成。图 2给出了RTGCV(GCV的平方根)的逐月变化曲线。可以看到，1961年1月至2014年12月，RTGCV波动具有一定的规律，基本在3.2%~5.5%范围内变化。20世纪60年代，RTGCV有逐渐降低趋势，70年代RTGCV为最低，80年代之后RTGCV呈逐渐上升趋势。RTGCV变化不仅具有年代际变化特征，同时具有周期为一年的年际变化特征。7月全国平均RTGCV最低，为3.58%；1月全国平均RTGCV最高，为4.20%；4、10月介于1、7月之间，分别为3.86%和3.94%。这与相对湿度的季节变化有关。通过分析冬、春、夏、秋季四个季节相对湿度的空间分布(图 3)得出：夏季，全国平均相对湿度为73.3%，有77.3%的台站平均相对湿度≥70.0%，有0.2%的台站平均相对湿度≤30.0%，全国各台站相对湿度普遍较高，空间差异不明显；冬季，全国平均相对湿度为64.9%，有43.0%的台站平均相对湿度≥70.0%，有0.8%的台站平均相对湿度≤30.0%，相对湿度西北低、东南高的空间特征较为突出，具有一定的空间差异。薄盘样条插值对空间差异较小拟合效果更好，因此，冬季插值误差相对夏季偏高。

2.2 误差分析

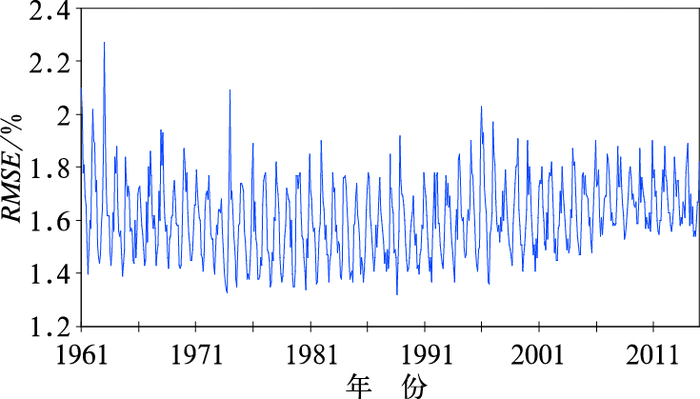
均方根误差(RMSE)也是常用的评估插值效果的指标之一。均方根误差是所有样本取出输入误差后的预计误差，相当于插值过程的真实误差。由RMSE的逐月变化曲线(图 4)可以看到：RMSE基本在1.2%~2.0%变化。其中，1961—1965年均方根误差相对较大。受相对湿度季节变化影响，RMSE也呈现出以一年为周期的变化，一般在夏季7、8月最小，冬季12、1月达到最大，这与冬季相对湿度空间差异较大有关。经统计，1961年以来相对湿度格点月值平均RMSE为1.62%。表明格点数据具有比较好的精度和较为理想的插值效果。

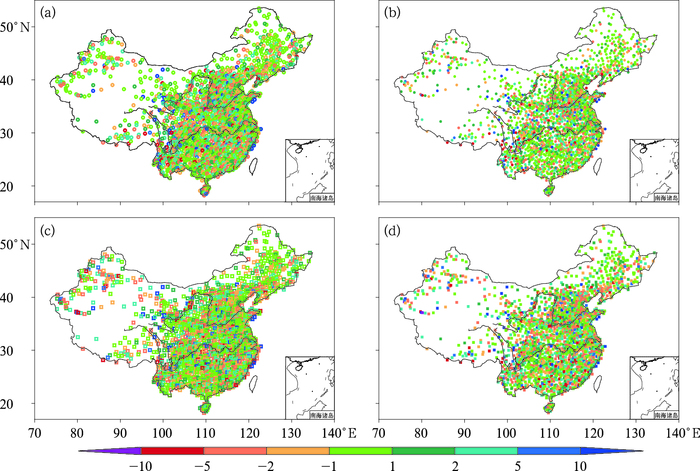
图 5为各季节插值平均偏差(MBE)空间分布。可以看出，无论哪个季节，无显著的区域特征，即在我国各个地区均可能出现偏差较大和偏差较小的台站，并且各种偏差频率分布特征比较相近。全国范围内，冬、春、夏、秋季分别有36.3%、38.4%、38.3%、34.1%台站MBE在±1%/月以内；95.2%、94.8%、96.8%、95.8%台站MBE在±5%/月以内；平均偏差分别为0.002%/月、0.013%/月、0.008%/月、0.007%/月。分析值与站点实测值间的相关系数R平均达0.89(通过0.01的显著性检验)。

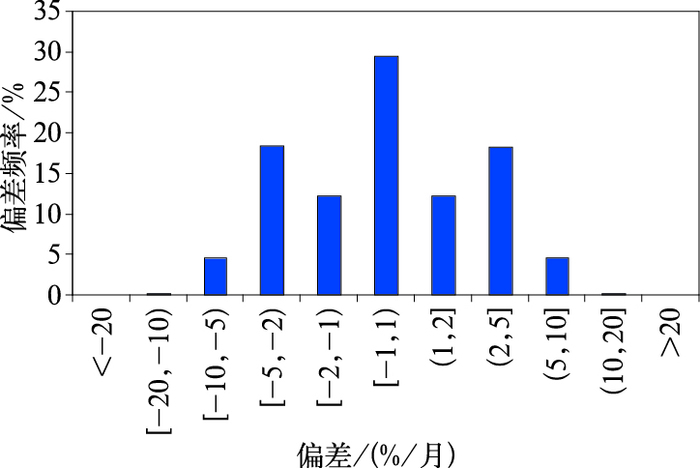
分别统计出不同偏差区间内样本的频率分布(图 6)。29.5%的样本，其分析值与站点实测值间的偏差在±1%/月以内；62.1%的样本，其分析值与站点实测值间的偏差在±2%/月以内；90.5%的样本，其分析值与站点实测值间的偏差在±5%/月以内。

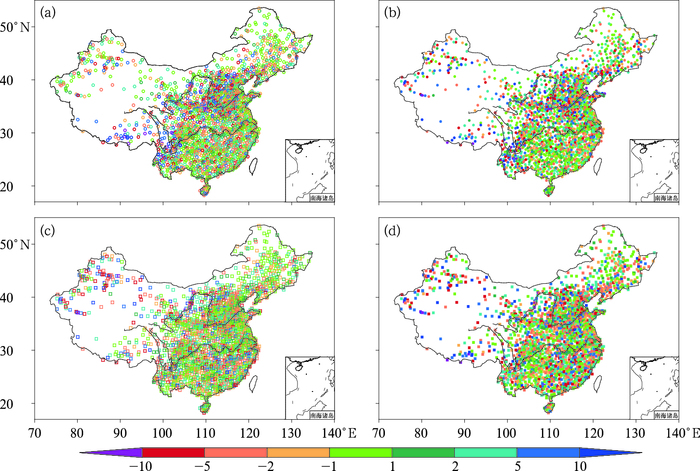
相对误差(RBE)为偏差与实测值间的比值。可以体现出误差相对于原始观测的量值。图 7给出的是1961—2014年各台站平均相对误差空间分布。可以看出，不同的季节，相对湿度插值误差空间特征差异较小。我国西北地区、西南地区、台站稀疏地区相对误差偏大。这与插值过程中，曲面的拟合效果有关，台站较少的地区，曲面拟合效果较差，因此，RBE也偏大。经统计，2400余站中，冬、春、夏、秋季分别有23.8%、23.6%、26.5%和21.5%台站RBE在±1%/月以内；79.0%、76.9%、84.6%和77.6%台站RBE在±5%/月以内；平均RBE分别为0.431%/月、0.439%/月、0.286%/月和0.382%/月。

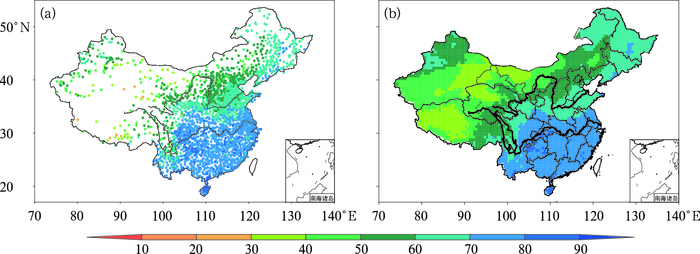
2.3 累年空间分布

图 8给出了1961—2014年累年平均站点及格点年相对湿度分布。对比两者发现，CR数据集能够较好地刻画出基于站点观测得到的我国相对湿度主要空间特征，较好地反映出我国自东南地区向西北地区相对湿度逐渐减小的大趋势。长江以南地区，格点数据集可以反映福建、贵州省内部分地区相对湿度较周围偏高的区域特征；黄河以南长江以北地区，格点数据集可以反映出我国南湿北干的纬度特征；西北地区，数据集也客观地反映了天山南北麓、塔里木盆地等大地形附近相对湿度的变化特征。但是，格点数据集也平滑掉了范围很小的相对湿度极值中心，由于我国西部台站稀少，尤其在青藏高原有大片区域只有零星的几个台站，格点数据集对该地区空气相对湿度特征的刻画是否合理很难给出定性、定量的判断。

2.4 气候趋势分析

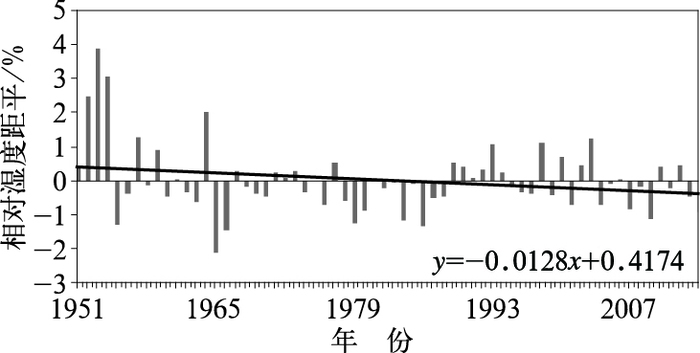
能否正确地反映气候变化趋势也是评估格点数据集质量的重要指标。由CR数据集得到的中国相对湿度长时间序列及其变化趋势(图 9)可知，近64年来中国年平均相对湿度呈减小趋势。线性趋势为0.12%/10年，通过了0.10的显著性水平检验。王遵娅等(2004)分析了50年来中国年平均相对湿度变化趋势，认为1954—2000年中国年平均相对湿度呈略减小趋势。沈艳等(2008)分析了近50年中国年平均水汽压的线性趋势，表明水汽压有显著升高的趋势。这是由于相对湿度是空气中实际水汽压与同时刻气温下的饱和水汽压之比，而21世纪以来气温持续升高，因此饱和水汽压增大。水汽压与饱和水汽压均有升高趋势，因此，相对湿度存在减小趋势就成为可能。

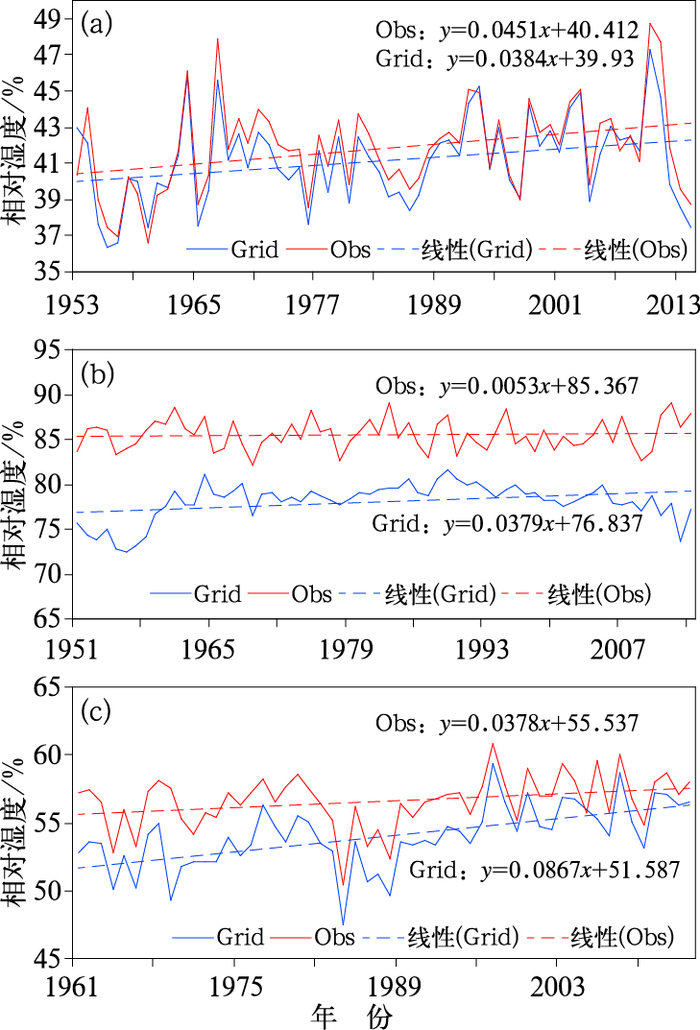
我国地形复杂，起伏较大，因此进一步分析了不同高度海拔台站实测相对湿度与对应网格值的关系。选取了玉门、峨眉山、嘉黎三个台站，验证CR数据集对高海拔台站气候变化趋势的描述水平。表 2给出了三个代表性台站海拔高度、台站实测值与台站所在网格值的相关系数及实测值序列与网格值序列的趋势方程。分析可知，玉门、峨眉山、嘉黎三个站台站实测值序列与对应网格值序列相关系数均通过0.01显著性检验，分别为0.94、0.99、0.85，并且三个台站实测值与网格值均具有一致的气候变化特征，即相对湿度呈升高趋势。说明在不同高度海拔地区，得到的相对湿度格点值在变化趋势上能较准确地代表实测值。玉门站多年实测平均相对湿度为41.8%，对应网格多年平均相对湿度为41.1%，两者非常接近；峨眉山站分别为85.5%和78.1%，网格值偏低7.4%；嘉黎站分别为56.6%和54.0%，网格值稍偏低2.6%。由于DEM值为每个网格内地形曲面的平均值，而峨眉山和嘉黎站海拔高度较该网格内平均地形偏高，

因此两个台站平均相对湿度实测值与网格值的差异可能与DEM与台站海拔高度的差异有关。

3 结论

通过对“中国地面均一化相对湿度0.5°×0.5°格点数据集(Ⅴ1.0)”的研制和插值误差分析，主要得到以下结论：

(1) 在广义交叉验证中，RTGCV波动具有一定的规律，在1.0%~2.0%范围内变化，且具有显著的周期特征。由于夏季相对湿度空间差异较冬季不明显，因此，冬季插值误差相对夏季偏高。1961年以来相对湿度格点月值平均均方根误差为1.62%。表明格点数据具有比较好的精度和较为理想的插值效果。

(2) 全国范围内，冬、春、夏、秋季分别有36.3%、38.4%、38.3%、34.1%台站偏差在±1%/月以内；95.2、94.8%、96.8%、95.8%台站偏差在±5%/月以内；平均误差分别为0.002%/月、0.013%/月、0.008%/月、0.007%/月。分析值与站点实测值间的相关系数R平均达0.89(通过0.01的显著性检验)。29.5%的样本，其分析值与站点实测值间的偏差在±1%/月以内；62.1%的样本，其分析值与站点实测值间的偏差在±2%/月以内；90.5%的样本，其分析值与站点实测值间的偏差在±5%/月以内。

(3) 各个季节，相对湿度插值误差没有显著空间特征。我国西北地区、西南地区、台站稀疏地区相对误差偏大。冬、春、夏、秋季分别有23.8%、23.6%、26.5%、21.5%台站相对误差在±1%/月以内；79.0%、76.9%、84.6%、77.6%台站相对误差在±5%/月以内；平均相对误差分别为0.431%/月、0.439%/月、0.286%/月、0.382%/月。

(4) CR数据集能够比较细致、准确地反映我国相对湿度场的主要空间特征。能够较好地展现长江以南地区、黄河以南长江以北地区、西北地区、天山南北麓、塔里木盆地等大地形的相对湿度变化特征。由于青藏高原台站稀少，格点数据集对该地区空气相对湿度特征的刻画是否合理很难给出定性和定量的判断。无论针对全国平均相对湿度序列，还是不同海拔高度代表站年平均相对湿度序列，CR数据集均能反映出与台站实测值基本一致的气候变化趋势。