2. 南京信息工程大学气象灾害教育部重点实验室,南京 210044
2. Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science and Technology, Nanjing 210044
暴雨预报一直是天气预报中非常重要的问题,暴雨作为最常见的高影响天气过程之一,一直是广大气象工作者关注和研究的重点(陶诗言,1980)。近年来,随着中尺度数值预报模式的迅速发展,利用中尺度数值模式WRF(Weather Research and Forecasting)模式进行暴雨等灾害性天气预报已成为主流(Skamarock et al,2008; Kain and Fritsch, 1993)。
然而,在利用数值模式进行天气预报时,由于模式水平分辨率以及云微物理方案还不够完善,而大气湿对流通常发生在不能被模式分辨的更小尺度上,从而影响模拟效果。利用积云对流参数化方案,将对流通过参数化的方式包含在模式中,从而完善模拟效果(邓华等,2008)。一方面,大尺度环流强迫和控制积云对流的发生,而另一方面,积云对流反过来又通过感热、潜热和动量输送等反馈作用影响大尺度环流,两者相互作用,并进一步对暴雨的发生发展产生影响(熊喆,2014;徐道生等,2014;饶建等,2014;伍华平等,2009;王晓彬,2007)。研究表明,合适的积云对流参数化方案可以完善降水的模拟效果(伍华平等,2009;Jankov et al,2005;Rao et al,2007;Flaounas et al,2011;Bukovsky and Karoly, 2009;闫之辉和邓莲堂,2007;廖镜彪等,2012)。伍华平等(2009)选用七种微物理方案与三种积云对流方案进行组合来模拟湖南南部一次暴雨过程,发现在20 km格点分辨率下,Lin方案的组合基本都可以模拟出暴雨的范围,其中KF方案模拟的强降水位置最接近实况、强度也吻合;BMJ方案对强降水的模拟效果偏强;GD方案范围、强度均偏弱。邓华等(2008)采用三种积云对流参数化方案对华南一次强降水过程进行模拟; 结果显示SAS方案能较好地反映华南对流降水过程中对流激发的时空分布特征。Jankov et al(2005)针对8个夏季MCS个例,采用不同云微物理、积云对流以及边界层在内的18种方案组合进行模拟; 结果表明,没有一种方案在不同个例不同量级的降水模拟中占有绝对优势,积云对流参数方案的选择对预报结果影响最大;其中,KF方案在强降水的模拟中体现出优势。Rao et al(2007)利用Ferrier微物理方案及BMJ积云方案组合能较好地模拟印度的三次暴雨过程。
“7·21”北京特大暴雨过程为华北雨季罕见的强降水过程,相比华南、江淮等地区降水(李昀英等,2015;廖镜彪等,2012;伍华平等,2009;闫之辉和邓莲堂,2007;Pan and Wu, 1995),其突发性强,降水强度大,持续时间短,局地性强(朱乾根等,2007;周雪松等,2012),对流的激发状态及演变过程显著不同,对流降水和层云降水使得降水量在短时间剧烈增多,积云对流参数化在此次过程的模拟试验中起着十分重要的作用。本文针对“7·21”北京特大暴雨过程,进行Kain-Fritsch(eta)(KF)、Betts-Miller-Janjic(BMJ)、Grell-Devenyi(GD)、Simplified Arakawa-Schubert(SAS)这四种积云对流参数方案的对比试验。
因此,本文以“7·21”北京特大暴雨过程为例,分析不同对流参数化方案对降水的模拟效果,研究对流激发在时空分布上的特征以及预报降水量的影响因子,希望对今后极端暴雨模拟参数化的应用提供参考,对模式预报暴雨提供一定的借鉴作用。
1 “7·21”暴雨天气过程简介受高低空与中低纬系统共同配合作用,2012年7月21日北京地区出现了自1951年有气象观测记录以来最强的一次降水天气过程。7月21日00时至22日00时(以下均为UTC),最大降水量出现在房山区河北镇,降水量达460 mm,北京市城区最大降水量出现在石景山模式口,达328 mm,平均降雨量215 mm;其中,北京市的20个国家气象站中海淀、门头沟、霞云岭、石景山、房山5站突破建站极值(孙建华等,2013)。此次降水过程有锋前暖区和锋面降水组成,暖区降水持续时间长,小时雨量大,具有典型的“列车效应”(王宇虹等,2015;方翀等,2012)。
受本次强降水影响,北京地区出现严重城市内涝,引起严重的经济损失和人员伤亡,约160.2万人受灾,79人死亡,成灾面积47.9万亩(1亩≈666.67 m2),停产企业761家,因灾造成直接经济损失达116.4亿元(孙建华等,2013;孙继松等,2012)。
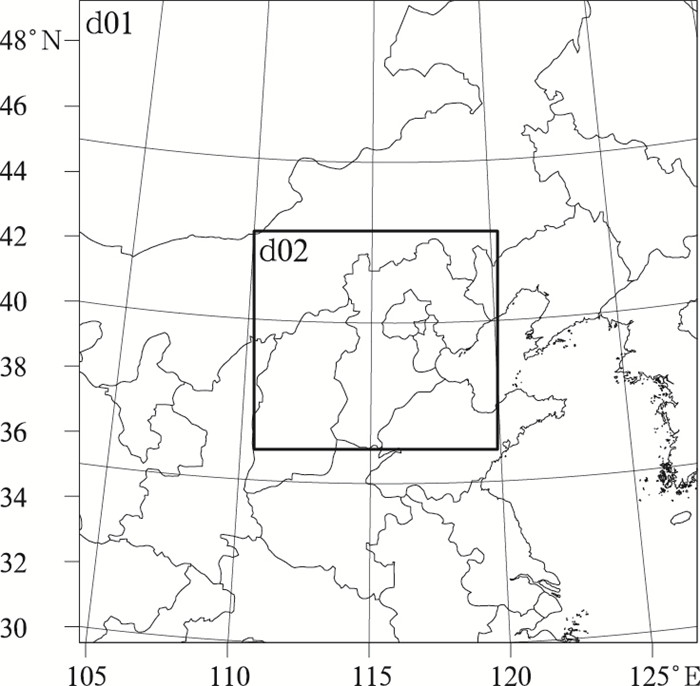
2 模式和试验方案简介 2.1 模式简介WRF模式是美国环境预测中心(National Centers for Environmental Prediction, NCEP)和国家大气研究中心(National Center for Atmospheric Research, NCAR)等联合研发的业务与研究共用的新一代高分辨率、完全可压非静力的中尺度数值天气预报模式,重点解决分辨率1~10 km,时效为60 h以内的有限区域天气预报和模拟问题。本文采用WRF V3.5.1版本,双重双向嵌套方案(图 1),区域中心为(40°N、115°E),粗细网格的水平分辨率分别为21.6和7.2 km,对应网格格点数分别为100×104和118×106;模式垂直方向分为30层,模式顶层气压为50 hPa。以NCEP一日四次的1°×1° FNL全球分析资料(Final Operational Global Analysis)作为模式的初边界条件,模式积分时间为2012年7月21日00时至22日00时(UTC),每5 min输出模式结果。降水观测资料为中国气象局提供的台站降雨量。
|
图 1 模式模拟区域 Fig. 1 Nested domains for WRF simulation |
本文选取NSSL 1-mom方案作为此次过程的云微物理参数化方案,该方案的确定是基于已有工作,在针对“7·21”北京特大暴雨过程进行17组不同云微物理方案的模拟试验后,评估各组试验对此次特大暴雨过程的模拟能力以及比较其云中水成物演变特征,从而确定最优的NSSL 1-mom云微物理方案(徐之骁和徐海明,2016)。在此基础上,模式的初始边界条件和其他物理过程方案保持不变,包括YSU行星边界层方案,Dudhia短波辐射方案,RRTM长波辐射方案,MM5 Monin-Obukhov近地面层方案以及NOAH陆面过程方案。
设计了WRF V3.5.1模式中4种积云对流参数化方案:Kain-Fritsch(eta)(KF)、Betts-Miller-Janjic(BMJ)、Grell-Devenyi(GD)和Simplified Arakawa-Schubert(SAS)方案(Kain,2004;Bukovsky and Karoly, 2009;Flaounas et al,2011;Grell and Devenvi, 2002;Grell,1993;Pan and Wu, 1995;王德立等,2013)。对“7·21”北京特大暴雨过程进行多组试验,探讨不同积云方案模拟的对流激发在时间和空间上的差异,并对降水预报的影响,比较何种方案模拟的对流激发与实况最为接近。当网格格距小于5~10 km时,不使用积云参数化方案(Grell and Devenvi, 2002),重点分析细网格的水平分辨率为7.2 km的区域。
2.3 检验方法本文利用相关系数、TS(Threat Score)评分和误差分析等方法来评估模式模拟雨带的分布和强度与实况之间的差异,定量地表示不同积云方案模拟降水的效果。
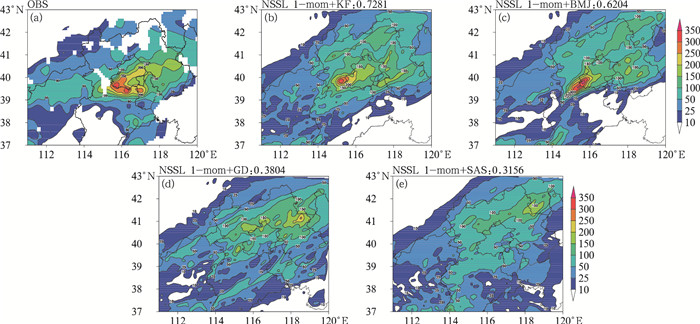
3 降水量对比分析和对流激发的时空特征 3.1 降水量对比分析图 2给出了4种积云对流方案模拟的24 h累积降水分布以及与站点降水量的相关系数。与实况降水对比可以看出,KF和BMJ方案的相关系数较高,达到0.6以上,而GD和SAS方案较低,相关系数不超过0.4。
|
图 2 2012年7月21日00时至22日00时24 h降水实况(a,OBS)和不同积云对流参数化方案模拟结果(b, c, d, e) (单位:mm)及与站点降水量的相关系数(位于图上框上方) Fig. 2 Observed (a, OBS) and simulated precipitation (unit: mm) with different cumulus parameterization schemes (b, c, d, e) from 0000 UTC 21 to 0000 UTC 22 July. Correlation coefficients between simulated and observed precipitation are also shown at top of each panel |
此次过程中华北大部分地区均出现了较强降水,京津冀等地有强降雨发生,北京地区的特大暴雨主要发生在西南部山区(俞小鼎,2012)。各试验都能模拟出西南—东北走向的大致雨带,但对中尺度雨团的模拟区别很大,尤其是北京西南部强降水中心。KF方案能够模拟出位于北京西南部的降水中心,并且雨带位置与实况最吻合,位置较实况略偏西约30~40 km左右,300 mm以上的暴雨中心强度和150 mm以上的雨带分布也与实况较为一致。BMJ方案明显增大了强降水区的范围和强度,特大暴雨中心强度达到350 mm以上,但漏报了华北南部地区降水,相比较下,GD和SAS方案的模拟效果不理想,基本没有模拟出北京西南部的强降水中心,大暴雨雨带分布零散。
表 1可以看出,大暴雨量级TS评分差异较为明显,模拟能力差别较大,说明不同积云对流参数化方案对强降水中心的模拟效果有着重要的影响,总体上KF和BMJ方案对强降水的模拟效果较好,其中KF方案的效果更好。由于KF方案中采用了上升气流与下沉气流的云模式,考虑积云对流活动耗尽对流有效位能,从而降水效率较高,预报效果较优;而GD等方案不能预报储存于天气系统中的对流有效位能,从而降低了降水效率(伍华平等,2009;林文实和黄美元,1998)。GD方案中云内上升及下沉质量通量则根据动力控制和有效浮力能来计算,云内潜热释放只是维持云的垂直质量通量,对模拟积云与大尺度环流相互作用的南方降水有一定效果(Grell,1993)。
|
|
表 1 不同积云对流方案对不同等级降水的TS评分结果 Table 1 TS scores for different level precipitation simulated by four different cumulus parameterization schemes |
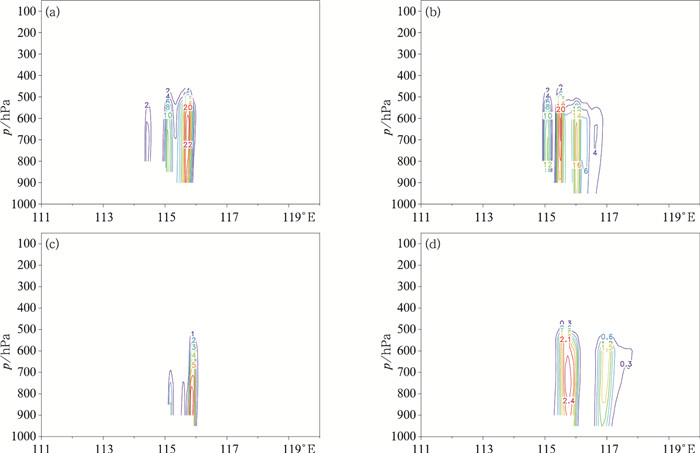
图 2所示,选择不同积云对流方案进行模拟时,中尺度雨团的强度和位置会有很大差别,这与不同方案判断激发对流的位置和强度的物理机制有关(邓华等,2008)。图 3是四个积云方案中模式积分第一步产生的降水量,KF和BMJ方案只在局部有降水产生,其中KF方案的降水范围稍大。而GD和SAS方案降水分布较为零散。对比模式积分最后一步降水可以看出,KF方案产生降水的面积从开始较小到不断扩大,雨带从西南向东北延伸,降水中心值从第一步0.24 mm到最后一步0.3 mm,逐渐增强。BMJ方案模拟的对流降水量从第一步的0.12 mm增长到0.2 mm。GD和SAS方案的降水量分布较之前更加零散,其中SAS方案的每一步降水基本都在0.2 mm左右,变化不大。
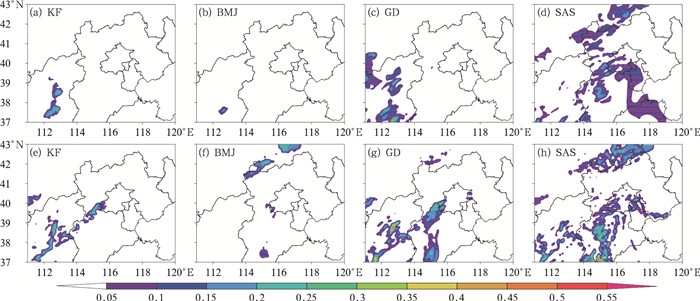
|
图 3 KF、BMJ、GD、SAS方案在模拟特大暴雨时的第一小时第一步对流降水量(a, b, c, d)和最后一步降水量(e, f, g, h)的分布(单位:mm) Fig. 3 The first-hour first-step convective precipitation (a, b, c, d) and the final-step precipitation (e, f, g, h) in 24 h from 0000 UTC 21 to 0000 UTC 22 July simulated by KF, BMJ, GD, SAS schemes (unit:mm) |
由于KF方案需要较长的模式启动时间,同时判断降水产生条件相对严格,因此对流开始激发时产生雨区面积和降水量都不大,落区位于山西省东部区域,随着模式的积分才出现了明显的大暴雨中心,这在表 1也得到印证(Pan and Wu, 1995)。降水的初始触发影响到后期的降水形态(图 2),相比KF和BMJ方案产生较为集中的降水,GD和SAS方案的降水开始比较零散,致使24 h累积降水也没有出现大暴雨。
选取降水发生期间高低层平均假相当位温差来表征对流激发(图 4),KF和BMJ方案激发对流较强且分布主要集中在北京西南部地区,KF方案的范围更大一些。GD和SAS方案的分布更广、更为零散,平均差值 < -2 K的区域较小。GD方案的对流稍弱,SAS方案则没有较强的对流中心,分布也较为平均,在主要降水落区,平均差值几乎没有 < -1.8 K的区域。有集中降水中心的方案,其激发的对流较强,位置也与强降水落区一致;反之,则降水分布较平均,没有明显的强降水中心。
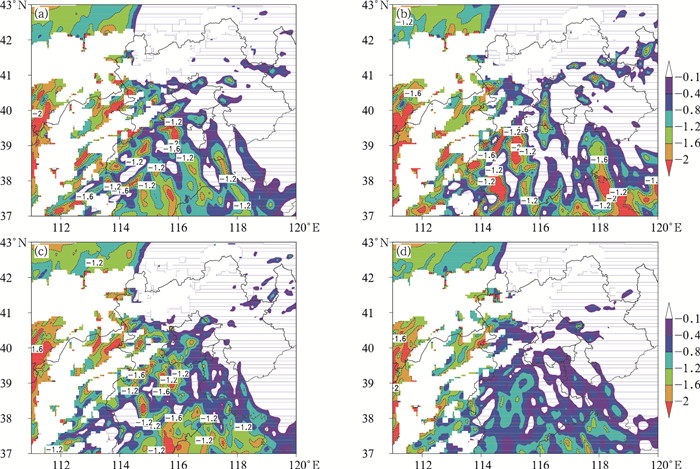
|
图 4 主要降水期间500 hPa与850 hPa的平均假相当位温差(单位:K) (a)KF,(b)BMJ,(c)GD和(d)SAS方案 Fig. 4 Difference of average pseudo-equivalent temperatures between 500 hPa and 850 hPa during the main precipitation (unit:K) (a) KF, (b) BMJ, (c) GD, and (d) SAS schemes |
根据此次过程国家基本站最大日降水量霞云岭站(39.7°N、115.7°E)的1 h雨量序列图,由图 5a霞云岭降水过程可细分为三个阶段:21日02—08时为第一阶段暖区降水;21日09—11时为第二阶段锋面强降水;21日12—18时为第三阶段锋后降水。暖区降水过程持续7 h,累积降水量达128.4 mm;强锋面降水持续3 h,累积降水量157.7 mm,占过程雨量的46.7%,这段时间的降水强度大,降水效率高,是预报员没有估计到的(谌芸等,2012)。此过程降水主要由长时间的暖区降水和超强的锋面降水构成。
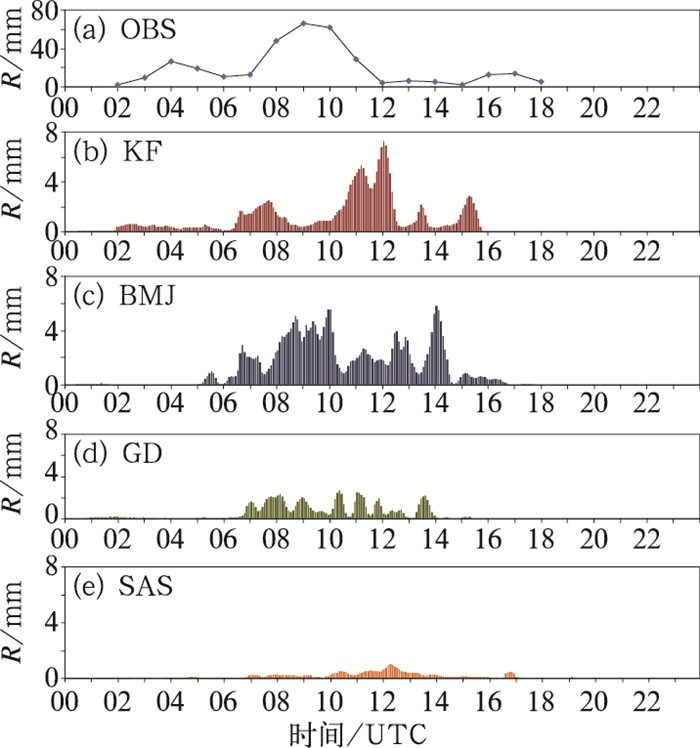
|
图 5 最大日降水量霞云岭站逐小时观测降水量(a)和KF(b)、BMJ(c)、GD(d)、SAS(e)方案模拟的该站每时间步长降水量 Fig. 5 Observed hourly precipitation of maximum daily precipitation at Xiayunling Station (a) and each step precipitation simulated by KF (b), BMJ (c), GD (d), SAS (e) schemes |
对比不同方案每步(300 s)的降水输出,KF方案模拟降水的三个阶段划分较为明显,过程降水主要由暖区降水和锋面降水构成,对流的激发在时间上与实况相同。BMJ方案在降水较大时段激发出的降水较多,持续时间较长,强降水中心明显。相反,GD和SAS方案在主要降水时段激发的降水偏少,SAS方案激发的降水较为平均,无法模拟出量级较大的降水。相比实况,四种方案模拟的降水量均明显偏弱。
4 模拟降水量差异的讨论霞云岭站作为此次特大暴雨过程最大日降水量基本站,降水阶段性特征明显,因此我们选取霞云岭站上空的物理量进行诊断分析。
通过对比霞云岭站上空的垂直速度、相对湿度和假相当位温随时间的变化(图 6),结合图 5,可以看出各方案在主要降水时段21日06—16时的相对湿度相差不大,从900~300 hPa之间基本都能达到90%以上。垂直方向上,KF和BMJ方案的假相当位温梯度较大,在较大对流降水时刻21日09—15时更为明显。KF方案在21日06时,假相当位温随高度递减,触发对流降水,在12时左右出现垂直速度中心,达4 m·s-1,并从600 hPa向高层延伸至300 hPa,与地面降水极值时段相对应。BMJ方案则在21日06—16时都有不稳定能量的触发,存在持续性对流降水,同时假相当位温线较密,垂直方向上梯度较大,在08—15时地面有较大降水时,最大值达到2 m·s-1,并延伸至200 hPa高度以上。强的对流通常要在对流层的中层有强烈的上升运动,KF和BMJ方案在此高度的垂直速度能达到2~3 m·s-1,有利于强对流的发生发展。相对而言,GD和SAS方案在降水集中时段站点上空的假相当位温线较稀疏,垂直方向上梯度较小,速度大值区基本在500 hPa以下,GD方案垂直速度最大值为1 m·s-1,而SAS方案仅为0.4 m·s-1,所以垂直速度过小是影响降水量偏少的可能原因之一。
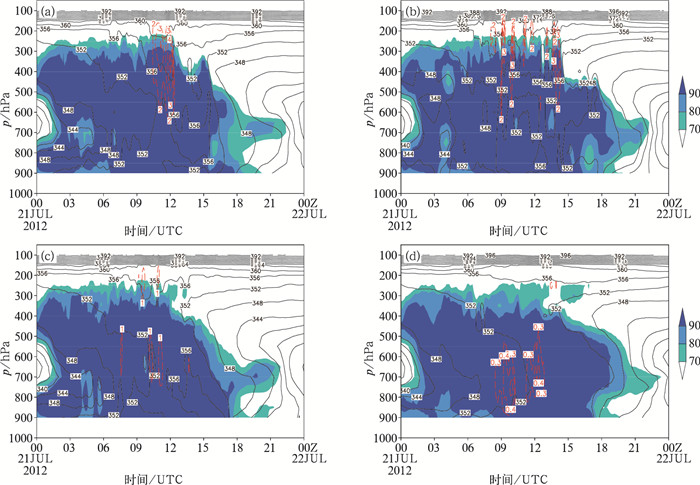
|
图 6 霞云岭站2012年7月21日00时至22日00时相对湿度(阴影表示相对湿度>70%)、假相当位温(黑色实线,单位:K)和垂直速度(红色虚线,单位:m·s-1)时间-高度剖面图(a)KF,(b)BMJ,(c)GD和(d)SAS方案 Fig. 6 Time-height cross sections of relative humidity (shading >70%), potential pseudo-equivalent temperature (black solid line, unit: K), and vertical velocity (red dotted line, unit: m·s-1) at Xiayunling Station (a) KF, (b) BMJ, (c) GD, and (d) SAS schemes |
图 7给出了在各方案模拟较大降水时刻(21日12时)沿强降水中心霞云岭站(39.7°N)作垂直速度和水汽通量散度的垂直剖面图。KF方案中模拟暴雨区上空800 hPa左右有水汽通量的辐合,值达到-16×10-8 g·cm-2·hPa-1·s-1,高层辐散,中心值达到4×10-8g·cm-2·hPa-1·s-1以上,造成抽吸作用,在500 hPa对流层中层有垂直速度中心,达4 m·s-1,上升运动强烈,低层辐合,低空急流为暴雨区输送水汽,高低空的配置有利于强降水的发生。GD和SAS方案在21日12时暴雨中心上空底层的水汽通量散度较弱,仅为-4×10-8g·cm-2·hPa-1·s-1,上升运动也较弱,GD方案在对流层低层最大垂直速度为0.8 m·s-1,SAS方案为0.6 m·s-1,较弱的动力条件和水汽条件难以维持强降水的发生发展。
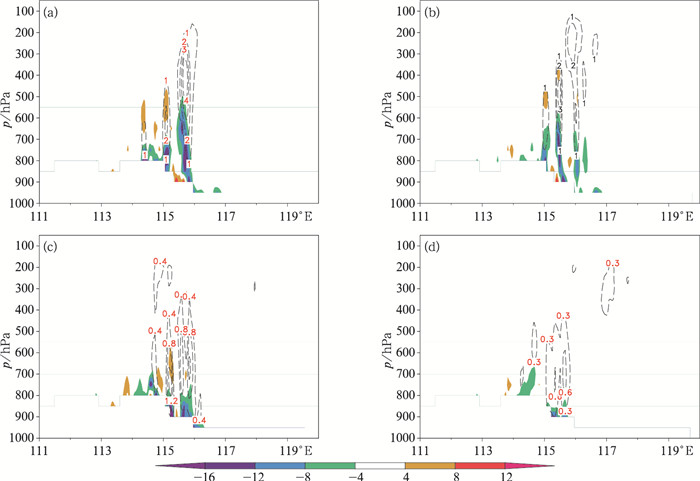
|
图 7 012年7月21日12时各积云对流参数化方案模拟的沿所在纬度(39.7°N)垂直速度(黑色虚线,单位:m·s-1)和水汽通量散度(阴影,单位:10-8 g·cm-2·hPa-1·s-1)剖面图(a)KF, (b)BMJ, (c)GD和(d)SAS方案 Fig. 7 Latitude-height cross sections of vertical velocity (black dotted line, unit: m·s-1) and moisture flux divergence (shading, unit:10-8 g·cm-2·hPa-1·s-1) along 39.7°N of Xiayunling Station at 12 UTC 21 July 2012 (a) KF, (b) BMJ, (c) GD, and (d) SAS schemes |
在较大降水时刻21日12时沿39.7°N作雨水混合比剖面图(图 8),发现大暴雨区上空800~600 hPa高度上,KF方案最大雨水混合比为22 g·kg-1,BMJ方案为20 g·kg-1,对应暴雨区上空的最大上升区(图 7)。而GD和SAS方案模拟的雨水混合比最大值分别为5和2.2 g·kg-1,较大的雨水混合比差异也说明了不同积云对流方案模拟降水强弱的原因。
综上所述,主要降水期间,KF和BMJ方案模拟的大暴雨区上空有强的上升运动,并延伸至200 hPa高度以上,假相当位温在垂直方向上的梯度较大,充沛的水汽条件和高低空的配置有利于强降水的发生。而GD和SAS方案在强降水发生时,假相当位温线较稀疏,上升运动较弱,水汽条件的不足都难以维持强降水的发生发展,24 h累积降水量也较弱。各积云对流方案计算的物理量不同正是暴雨不同模拟结果的客观写照。
5 对流降水和层云降水“7·21”北京特大暴雨由对流降水和层云降水组成,其云微物理过程、动力环流、潜热释放等均存在显著差异,同时这两个区域也相互作用、密不可分(Houze,1989;董昊等,2012)。
5.1 降水区域的划分标准参照Xu(1995)和Luo et al(2010)的划分方法,考虑对流性降水和层云性降水过程的差异,将模拟的区域分为晴空区和云区,云区又分为深对流区、浅对流区以及层云区;具体划分标准从对流系统的动力结构、格点柱水凝物的分布、深对流区域的垂直速度强度及分布、浅对流区域的雨水云水含量及冰相水凝物的含量等方面综合考虑(Houze,1977;Zipser,1946;董昊等,2012;万子为等,2015)。
将模拟试验结果逐5 min输出,依据上述的诊断方法进行区域划分,并对划分区域结果进行验证。21日11时对KF方案模拟的结果进行区域划分(图 9c),其深对流区域对应着实况观测强回波区(40 dBz以上)(图 9a),其浅对流区域没有产生降水,在雷达回波上没有显示。比较此次试验的其他时刻以及各组积云方案模拟的结果,与图 9的定性相一致,说明对模拟结果的区域划分较为合理。
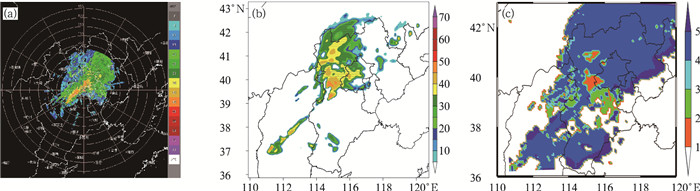
|
图 9 2012年7月21日11时北京雷达观测3 km高度雷达回波(a)(单位:dBz),KF方案模拟的700 hPa高度雷达回波(b)(单位:dBz)和模拟结果诊断得到的区域划分情况(c) (白色:晴空区,橙色:深对流区,绿色:浅对流区,天蓝:深对流周边,深蓝:伴有地面降水的层云区域,紫色:无地面降水的层云区域) Fig. 9 Observed radar reflectivity of Beijing radar at the height of 3 km (a), reflectivity at 700 hPa by KF scheme (b) at 1100 UTC 21 July 2012 (unit: dBz) and classification of the various regions using the simulation result of KF scheme (c) (white, orange, green, light blue, deep blue and purple represent the regions of clear sky, deep convection, shallow convection, deep convection surrounding, stratus cloud with surface rainfall and stratus cloud without surface rainfall) |
对所划分的深对流、浅对流和层云区域进行区域平均的地面降水率和区域面积的计算(董昊等,2012)。
对比各组参数化方案模拟的地面累积降水区域平均值(图 10a),KF方案模拟的降水平均值最大,达39 mm;BMJ和GD方案的降水平均值接近,都在36 mm左右;SAS方案最少,为35.4 mm。从总体的区域平均地面降水率的时间演变来看(图 10b),KF和BMJ方案的降水率高于GD和SAS方案,在降水初期的几个小时内,各积云对流参数化方案模拟的降水率相差不大,在08—13时主要强降水时段内,KF和BMJ方案降水效率明显较高,其中BMJ方案在11时模拟的降水率高达到0.2 mm·h-1;在降水后期,BMJ方案明显减小,而KF方案依旧维持在较高水平。
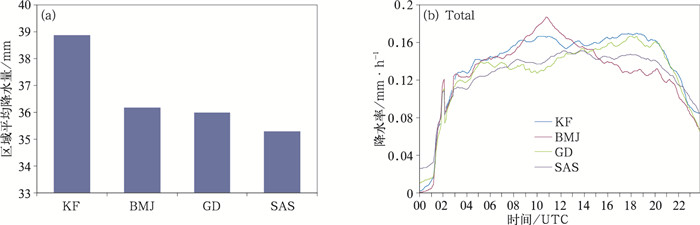
|
图 10 各组积云对流参数化方案模拟试验区域平均的24 h地面累积降水(a)和区域平均逐5 min降水率的时间演变(b) Fig. 10 Area-averaged 24h accumulated surface rainfall (a) and temporal evolution of domain-averaged surface rainfall rates at 5-min inerval from the four groups of simulations (b) |
通过计算,发现深对流区域的地面降水率相比浅对流区和层云区域大一个量级,因此重点讨论(图 11)。在深对流区域中,采用KF和BMJ方案模拟的初期降水在01时以后,降水率增长迅速,总体高于GD和SAS方案,BMJ方案模拟的降水率在02时达1.5 mm·h-1。较高深对流区的降水率使得模拟的强降水中心雨量较大。图 11b中,KF方案模拟深对流区域面积在四种方案中并非最高,而降水效率较高,这与KF方案本身的设计有关,此方案判断降水产生的条件相对严格。各方案中,层云区域面积占所有分析区域面积的比重都较高(图略),SAS方案达到38%以上,说明模拟的较多为层云降水,降水量级较小,降水效率不高,无法模拟出强暴雨中心。
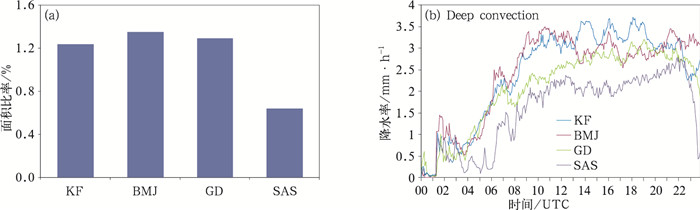
|
图 11 各组积云对流参数化方案模拟试验深对流区域面积占总分析区域面积百分比的时间平均值(a)和深对流区域逐5 min降水率的时间演变(b) Fig. 11 Fractions of areas of the deep convection region averaged over the entire simulation period (a) and Temporal evolution of fractions of areas of the deep convection region at 5-min interval from the four groups of simulations (b) |
综上,KF和BMJ方案在整个区域及深对流区模拟的降水效率都较高,使得24 h累积降水量较大,降水预报的效果较好。SAS方案模拟试验模拟的基本为层云区域,无法模拟出强降水中心。
6 结论本文依据已有工作,挑选WRF V3.5.1版本中针对本次降水过程模拟最优的云微物理参数化方案NSSL 1-mom参数化方案,分别与KF(Kain-Fritsh)、BMJ(Betts-Miller-Janjic)、GD(Grell-Devenyi)和SAS(Simplified Arakawa-Schubert)这四种不同的积云对流参数化方案组合,探讨“7·21”北京特大暴雨过程对不同积云对流参数化方案选择的敏感性,得到了以下几点主要结论:
(1) 不同积云对流参数化方案对强降水中心的模拟有着重要的影响。总体而言,KF方案在各量级降水的模拟中占有优势,KF方案整体效果较好,BMJ方案夸大了强降水区的范围和强度。而GD和SAS方案的模拟效果较差,大暴雨雨带分布零散。
(2) 各方案模拟的24 h累积降水分布与各自初始对流的激发状态紧密相关,KF方案的初始激发有明显的局地性;BMJ方案模拟的降水则增长较快;GD方案的每一步降水范围不断扩大,降水量也有所增长;SAS方案的降水激发开始相对较小,每一步降水量变化不大,最后一步降水量分布较之前更加零散。从对流激发的时间上看,KF方案模拟各降水阶段划分明显,与实况相符。BMJ方案在降水较大时段激发出的较多降水,并且持续时间相对较长。而GD和SAS方案激发的降水量偏少,无法模拟出较大量级的降水。
(3) 有强降水发生时,KF和BMJ方案模拟的大暴雨区上空有强的上升运动,假相当位温在垂直方向上梯度较大,充沛的水汽和高低空的配置都有利于强降水的发生。而GD和SAS方案的动力条件和热力条件都难以维持强降水的发生发展。各积云对流方案计算的物理量的不同正是暴雨不同模拟结果的客观写照。
(4) 通过对降水区域的划分,KF方案模拟试验在总区域的降水率变化较为平稳,并且维持在较高的水平;BMJ方案降水率波动较大,有明显的降水集中时段;SAS方案降水率较低,地面累积降水的区域平均值也较低。KF和BMJ方案深对流区的降水效率较高,24 h累积降水量较大,降水预报的效果较好。而SAS方案基本均为层云区域,无法模拟出强降水中心。
综合来看,KF积云对流参数化方案与NSSL 1-mom云微物理参数化方案的组合在模式中似乎能较好地模拟“7·21”北京特大暴雨过程以及对流激发的时空分布特征,然而本工作只是选取了一次有代表性个例,其结果并不能完全说明WRF模式对流参数化方案在北方降水过程的适用性问题,需更多的个例试验以完善结论。
谌芸, 孙军, 徐珺, 等, 2012. 北京特大暴雨极端性分析及思考(一)观测分析思考[J]. 气象, 38(10): 1255-1266. DOI:10.7519/j.issn.1000-0526.2012.10.012 |
邓华, 薛纪善, 徐海明, 等, 2008. GRAPES中尺度模式中不同对流参数化方案模拟对流激发的研究[J]. 热带气象学报, 24(4): 327-334. |
董昊, 徐海明, 罗亚丽, 2012. 云凝结核浓度对WRF模式模拟飑线降水的影响:不同云微物理参数化方案的对比研究[J]. 大气科学, 36(1): 145-169. |
方翀, 毛冬艳, 张小雯, 等, 2012. 2012年7月21日北京地区特大暴雨中尺度对流条件和特征初步分析[J]. 气象, 38(10): 1278-1287. DOI:10.7519/j.issn.1000-0526.2012.10.014 |
李昀英, 寇雄伟, 方乐锌, 等, 2015. 中国东部云-降水对应关系的分析与模式评估[J]. 气象学报, 73(4): 766-777. DOI:10.11676/qxxb2015.042 |
廖镜彪, 王雪梅, 夏北成, 等, 2012. WRF模式中微物理和积云参数化方案的对比试验[J]. 热带气象学报, 28(4): 461-470. |
林文实, 黄美元, 1998. 积云参数化方案研究的现状[J]. 热带气象学报, 14(4): 374-379. |
饶建, 任荣彩, 杨扬, 2014. 热带加热异常影响冬季平流层极涡强度的数值模拟[J]. 大气科学, 38(6): 1159-1171. |
孙继松, 何娜, 王国荣, 等, 2012. "7·21"北京大暴雨系统的结构演变特征及成因初探[J]. 暴雨灾害, 31(3): 218-225. |
孙建华, 赵思雄, 傅慎明, 等, 2013. 2012年7月21日北京特大暴雨的多尺度特征[J]. 大气科学, 37(3): 705-718. DOI:10.3878/j.issn.1006-9895.2013.12202 |
陶诗言, 1980. 中国之暴雨[M]. 北京: 科学出版社, 1-225.
|
伍华平, 束炯, 顾莹, 等, 2009. 暴雨模拟中积云对流参数化方案的对比试验[J]. 热带气象学报, 25(2): 175-180. |
王宇虹, 徐国强, 贾丽红, 等, 2015. 太行山对北京"7·21"特大暴雨的影响及水汽敏感性分析的数值研究[J]. 气象, 41(4): 389-400. DOI:10.7519/j.issn.1000-0526.2015.04.001 |
王晓彬, 2007. 积云对流参数化方案对东亚夏季模拟对比[J]. 中国民航大学学报, 25(5): 61-64. |
王德立, 徐国强, 贾丽红, 2013. GRAPES的积云对流参数化方案性能评估及其改进试验[J]. 气象, 39(2): 166-179. DOI:10.7519/j.issn.1000-0526.2013.02.005 |
万子为, 王建捷, 黄丽萍, 等, 2015. GRAPES-Meso模式浅对流参数化的改进与试验[[J]. 气象学报, 73(6): 1066-1079. DOI:10.11676/qxxb2015.071 |
熊喆, 2014. 不同积云对流参数化方案对黑河流域降水模拟的影响[J]. 地球科学进展, 29(5): 590-597. DOI:10.11867/j.issn.1001-8166.2014.05.0590 |
徐道生, 陈子通, 钟水新, 等, 2014. 对流参数化与微物理过程的耦合及其对台风预报的影响研究[J]. 气象学报, 72(2): 337-349. DOI:10.11676/qxxb2014.017 |
徐之骁, 徐海明, 2016. 不同云微物理方案对"7·21"特大暴雨模拟的对比试验[J]. 气象科学, 36(1): 45-54. DOI:10.3969/2014jms.0096 |
闫之辉, 邓莲堂, 2007. WRF模式中的微物理过程及其预报对比试验[J]. 沙漠与绿洲气象, 1(6): 1-6. |
俞小鼎, 2012. 2012年7月21日北京特大暴雨成因分析[J]. 气象, 38(11): 1313-1329. |
周雪松, 阎丽凤, 孙兴池, 等, 2012. "2007[J]. 8.17"山东大暴雨的数值模拟和诊断分析[J].气象, 38(8): 960-970. |
朱乾根, 林锦瑞, 寿绍文, 等, 2007. 天气学原理和方法[M]. 北京: 气象出版社.
|
Bukovsky M S, Karoly D J, 2009.Precipitation simulations using WRF as a nested regional climate model.J Appl Meteor Climat, 48(10):2152-2159.
|
Flaounas E, Bastin S, Janicot S, 2011.Regional climate modelling of the 2006 West African monsoon:sensitivity to convection and planetary boundary layer parameterisation using WRF.Climate Dyn, 36(5-6):1083-1105.
|
Grell G A, 1993. Prognostic evaluation of assumption used by cumulus parameterizations[J]. Mon Wea Rev, 121(3): 764-787. DOI:10.1175/1520-0493(1993)121<0764:PEOAUB>2.0.CO;2 |
Grell G A, Devenvi D, 2002.A generalized approach to parameterizing convection combining ensemble and data assimilation techniques.Geophy Res Lett, 82(14):587-590.
|
Grell G A, Dudhia J, Stauffer D R, 1994.A description of fifth-generation Penn State/NCAR mesoscale model(MM5)[R].NCAR Technical Note TN-398+STR.
|
Houze R A, 1977. Structure and dynamics of a tropical squall-line system[J]. Mon Wea Rev, 105(12): 1540-1567. DOI:10.1175/1520-0493(1977)105<1540:SADOAT>2.0.CO;2 |
Houze R A, 1989. Observed structure of mesoscale convective systems and implications for large-scale heating[J]. Quart J Roy Meteor Soc, 115(487): 425-461. DOI:10.1002/(ISSN)1477-870X |
Jankov I, Gallus W A, Segal M, et al, 2005. The impact of different WRF model physical parameterizations and their interactions on warm season MCS rainfall[J]. Wea Forecasting, 20(6): 1048-1060. DOI:10.1175/WAF888.1 |
Kain J S, 2004. The Kain-Fritsch convective parameterization:an update[J]. J Appl Meteor, 43(1): 170-181. DOI:10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2 |
Kain J S, Fritsch J M, 1993.Convective parameterization in mesoscale models:The Kain-Fritsch scheme[C]//The representation of cumulus convection in numerical models.American Meteorological Society:Boston, MA.165-170.
|
Luo Y, Wang Y, Wang H, et al, 2010. Modeling convective-stratiform precipitation processes on a Mei-Yu front with the weather research and forecasting model:Comparison with observations and sensitivity to cloud microphysics parameterizations[J]. J Geophy Res, 115(115): 311-319. |
Pan H L, Wu W S, 1995.Implementing a mass flux convection parameterization package for the NMC medium-range forecast model[R].NMC Office Note 409:39.
|
Rao Y V R, Hatwar H R, Salah A K, et al, 2007. An experiment using the high resolution eta and WRF models to forecast heavy precipitation over India[J]. Pure Appl Geophys, 164(8): 1593-1615. |
Skamarock W, Klemp J B, Dudhia J, et al, 2008.A description of the advanced research WRF version 3[R].NCAR Technical Note NCAR/TN-475+STR.
|
Xu K M, 1995. Partitioning mass, heat, and moisture budgets of explicitly simulated cumulus ensembles into convective and stratiform components[J]. J Atmos Sci, 52: 551-573. DOI:10.1175/1520-0469(1995)052<0551:PMHAMB>2.0.CO;2 |
Zipser E J, 1946. Mesoscale and convective-scale downdrafts as distinct components of squall-line structure[J]. Mon Wea Rev, 105(12): 1568-1589. |
 2017, Vol. 43
2017, Vol. 43