2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
大气中的水汽在降水过程的形成和演变中起着至关重要的作用(王宇虹等,2015;王佳津等,2015;苗长明等,2015)。近年来,GPS(Global Position System)遥感技术提供了一种高时间分辨率和高精度的水汽信息解算方法,其解算思路为:GPS卫星发射的无线电信号穿越大气层时,受大气折射的影响,卫星信号到达接收机处时会产生延迟现象(到达时间变晚)。由于大气折射率与大气水汽信息密切相关,则通过测量卫星的这一延迟信号便可反算出天顶大气含水量(Bevis et al, 1992)和斜路径大气含水量(万蓉等,2015)。随着这一技术的不断发展,GPS天顶大气含水量PWV(Precipitable Water Vapor)不仅被广泛地应用于水汽(陈小雷等,2007;邹海波等,2010)、台风(丁金才等,2004)、暴雨(姚建群等,2005;楚艳丽等,2007;郝丽萍等,2013;张家国等,2013; 刘晶和杨莲梅, 2017)等监测业务和研究中,还被广泛地应用于数值模拟业务和研究中(Smith et al,2000;Benjamin et al,2010;李红莉等,2010;顾莹等,2010;陈敏等,2010;张晶等,2014;朱丰等,2014)。此外,GPS PWV资料还被用于检验探空湿度探测仪的精度(梁宏等,2012)和修正太阳光度计PWV反演模式参数(毕研盟等,2011)。可见,GPS PWV的精度在气象业务与科研中的重要性。
在GPS PWV的解算过程中,需要先解算出测站上空的天顶总延迟(zenith total delay, ZTD),而ZTD的解算又依赖于测站的精确定位。卫星导航定位主要用伪距测量来实现,其原理为:测站(卫星接收机)的经度、纬度和高度三个未知数,加上测站时钟与导航系统基准钟的钟差共四个未知数,在测站(接收机)同时收到4颗或以上的卫星信号的前提下(保证方程组能闭合有解),基于事先给出的概略坐标—早期卫星导航接收机也需要输入概略坐标(张守信,2001),最后再利用迭代法求解方程组,便可获得测站的精确位置(朱喜明和王存良,2004)。
上述研究表明,GPS PWV精度依赖于测站的定位,而测站的定位又与测站的概略坐标密切相关。那么测站的概略坐标对GPS PWV的解算有何影响?为了弄清楚这一问题,本文将利用同时拥有GPS监测和探空探测的江西南昌站的相关观测资料,运用GAMIT软件开展南昌站概略坐标变化对GPS PWV解算的敏感性试验,找出概略坐标对GPS PWV解算的影响规律,为提升GPS PWV的解算精度提供科学参考。
1 资料来源与GPS PWV的处理方法 1.1 资料来源本文所用的资料包含:时间分辨率为30 s一次的南昌地基GPS监测资料、每日2次(00时和12时,世界时下同)南昌探空资料、逐时南昌地面气象观测资料、30 s一次的长基线[中国拉萨(LHAZ)、蒙古乌兰巴托(ULAB)、菲律宾奎松市(PIMO)、和泰国曼谷(CUSV)四个站,见图 1]GPS监测资料以及精密星历文件。其中南昌地基GPS监测资料、南昌探空站资料和南昌地面气象观测资料(用于GPS PWV反演中气象文件的制作)均来源于江西省气象信息中心,4个长基线国际IGS跟踪站资料和精密星历文件来源于http://igscb.jpl.nasa.gov/。以上资料时间长度均为2016年4月10日(第101天)至8月8日(第160天)。

|
图 1 南昌(NANC)站和四个IGS国家跟踪站的分布 (数字表示相应两站的基线长度,单位:m) Fig. 1 Distribution of Nanchang GPS Station and four IGS GPS stations (Digit indicates the length of baseline, unit: m) |
目前高精度的GPS资料处理软件主要有美国麻省理工学院(MIT)开发的GAMIT软件、瑞士伯尔大学开发的Bernese软件以及美国喷气推进试验室开发的GIPSY软件。但由于GAMIT软件拥有开源、高精度、高速度等特点,目前已经被广泛地应用在GPS PWV解算中(Dixon et al, 1991;梁伟锋,2002;邹海波等,2013)。因此,本文选用2015年6月发布的GAMIT 10.6软件来处理GPS观测资料,但在利用GMAIT对GPS监测资料进行解算时,监测资料的时间序列需要达到一定的长度(一般不少于12 h)。而南昌地基GPS监测资料单个观测文件的时间序列长度仅为1 h,故在解算之前需要对其进行合并处理,本文采用美国卫星导航系统与地壳形变观测研究大学联合研发的TEQC(translation, editing and quality checking)软件对其先进行质量控制再进行合并处理,最终形成一个时间序列为24 h(00—23时)的观测文件。此外,在解算过程中还加入了LHAZ、ULAB、PIMO和CUSV四个长基线站的观测资料,以及赣州和上饶两个局地GPS观测站资料。
2 试验设置为了研究概略坐标变化对GPS PWV的影响,针对同时拥有探空和GPS监测的南昌站,本文共设计了13组试验,1组控制性试验(CTR)和12组敏感性试验(SES)。其中,CTR试验中南昌站的概略坐标选用江西省GPS/MET水汽解算系统输出的2016年5月南昌站经纬度的平均值(可视为南昌站的真实经纬度),12组SES试验中南昌站概略坐标的纬度与CTR保持一致(均为28.42888°N),但经度则以10 m等间隔逐渐向西偏移,概略坐标设置详见表 1。此外,在这13组试验中其他参数设置均是相同的,其中解(Choice of Experiment)采用松弛解(relax),分析类型(Type of Analysis)选用1-ITER,观测(Choice of Observable)选用LC_HELP,卫星最小高度角(Elevation Cutoff)设置为15°,大气参数Interval zen=1(生成GPS PWV数据的时间分辨率为1 h一次),固体潮改正(Etide model)为IERS03,天顶静力延迟模型采用改善后的Hopfield模型(邹海波等,2013),南昌、赣州和上饶三站的坐标约束COORD.CONSTR均设置为“99.99 99.99 99.99”,CUSV和ULAB的坐标约束COORD.CONSTR设置为“0.1 0.1 0.1”,LHAZ的坐标约束COORD.CONSTR设置为“1.0 1.0 1.0”,PIMO的坐标约束COORD.CONSTR设置为“0.05 0.05 0.05”,所有测站的FIX设置为NNN。
|
|
表 1 各组试验概略坐标信息 Table 1 The approximate coordinates of all tests |
对于GPS资料的解算精度和可靠性一般采用基线相对误差(基线重复率)、均方根残差(NRMS)和GPS PWV三个指标进行分析。
3.1 基线相对误差基线相对误差是衡量GPS定位和数据处理质量的重要指标之一(Dixon et al,1991;刘经南和葛茂荣,1995;梁伟锋,2002),它反映了观测时段内观测数据的离散程度(受观测资料质量、起算数据偏差等影响),高质量的GPS处理过程中基线相对误差较小,GAMIT软件解算的长基线(1000 km)的基线相对误差量级应该为10-9(Dixon et al,1991;刘经南和葛茂荣,1995)。基线相对误差计算公式为:
| $ R = {\rm{ }}\sqrt {\frac{{\frac{n}{{n - 1}}{\rm{ }}\sum\limits_{{\rm{ }}i = 1}^n {\frac{{({Y_i} - Y)}}{{\sigma _i^2}}} }}{{\sum\limits_{i = 1}^n {\frac{1}{{\sigma _i^2}}} }}} {\rm{ }} $ | (1) |
式中,n为同一基线总观测时段数,Yi为i时段解的基线在x、y和z方向分量或边长,σi2为Yi的方差,Y为Yi的加权平均值,其计算公式为:
| $ Y = {\rm{ }}\frac{{\sum\limits_{i = 1}^n {{Y_i}/\sigma _i^2} }}{{\sum\limits_{i = 1}^n {1/\sigma _i^2} }} $ | (2) |
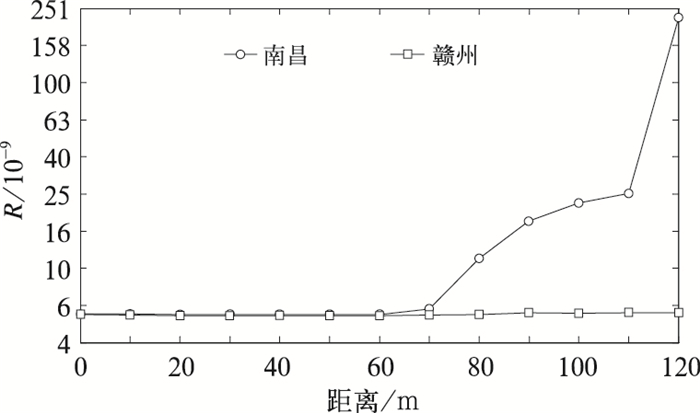
南昌站至各IGS跟踪站的基线长度(图 1)显示,南昌站至拉萨站的基线最长,为2398027.95 m。因此,本文选用南昌至拉萨的基线相对误差对各组试验的GPS的处理结果进行分析。各组试验2016年第101天至第160天平均的南昌至拉萨的基线相对误差(图 2)显示,CTR试验(南昌站概略坐标偏离真实点的距离为0 m)的相对误差为5.7×10-9,与刘经南和葛茂荣(1995)及李毓麟等(1996)的精度相当,完全满足GPS精度定位的要求。从图 2还可以看出,在南昌概略坐标偏离实际坐标60 m以内时,基线相对误差一致维持在5.7×10-9,但当概略坐标偏离实际坐标≥70 m以后,基线相对误差快速增大,当概略坐标的偏离程度达到80 m时,基线相对误差为1.2×10-8,当概略坐标的偏离程度达到90 m时,基线相对误差超过了2.0×10-8,超过了短基线( < 500 km)站一般的误差(李毓麟等,1996),当概略坐标与实际坐标偏离到达120 m时,基线相对误差剧增加至2.0×10-7以上,这完全不满足GPS精度定位的要求。图 2还显示,无论南昌站概略坐标如何变化,赣州至拉萨基线的相对误差始终保持一个固定值(5.7×10-9)附近,其他站至拉萨的基线相对误差也有类似的结果,这表明GAMIT软件处理GPS数据时某一站的概略坐标变化不会对其他站的定位产生明显的影响。
|
图 2 各组试验南昌至拉萨和赣州至拉萨的基线相对误差演变情况 Fig. 2 Evolution of the relative error of baseline from Nanchang to Lhasa, and from Ganzhou to Lhasa in each test |
均方根残差(normalized root mean square, NRMS)是从历元的模糊度解算中得出的残差(Dong and Bock, 1989),反映了时段解基线偏离其加权平均值的程度,也是衡量GAMIT解算结果的一个重要指标,NRMS的值越低表明GAMIT的解算结果越好,NRMS的值一般应小于0.3。若NRMS>0.5则反映解算过程中未去除大周跳、某一相关参数解算有误或存在一系列的模式问题(Herring et al,2015)。
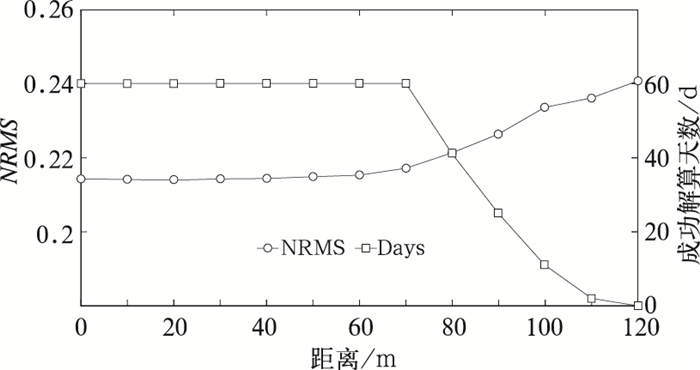
各组试验2016年第101天至第160天平均的NRMS演变(图 3)显示,当南昌站的概略坐标采用真实坐标时,GAMIT解算结果(Q文件)的NRMS为0.215,这表明GAMIT的解算结果较为理想。与基线相对误差类似,南昌概略坐标偏离实际坐标60 m以内时,NRMS一直维持在0.215附近。此后,随着南昌概略坐标与实际坐标偏离程度的继续增大,NRMS也开始逐渐增大,当南昌概略坐标与实际坐标偏离达到120 m时,NRMS为0.24,仍然符合GPS数据的解算的标准(小于0.3)。但事实上,NRMS反映的是所有站GPS解算结果的整体效果,不仅受单站概略坐标精度的影响,还与较大误差概略坐标站数的比例有关,当参与解算的观测资料仅有拉萨(IGS国际跟踪站)和南昌两站,且南昌的概略坐标与实际坐标偏离为120 m时(较大误差概略坐标站占50%的比例),NRMS超过了0.6。
|
图 3 各组试验中均方根残差和南昌站GPS PWV成功解算天数的演变情况 Fig. 3 Evolution of NRMS and the days of successful solving GPS PWV at Nanchang Station in each test |
获取高精度的GPS PWV是GPS数据解算的最终目标,为了评估各组试验对GPS PWV精度的影响,本文选用南昌站的探空PWV作为“观测值”进行对比分析。然而,探空探测中仅探测大气的温湿垂直剖面,而不探测PWV,PWV需要用以下公式计算得到:
| $ PWV = - {\rm{ }}\frac{1}{g}\int_{{P_{\rm{S}}}}^{{P_{\rm{T}}}} {q{\rm{d}}p} $ | (3) |
式中,PT为大气层顶的气压(本文设置为100 hPa),PS为地面气压,g=9.8 m·s-2为地球重力加速度,比湿q由以下公式计算得到。
| $ q = \frac{{0.622e}}{{p - 0.378e}} $ | (4) |
式中,水汽压e(单位:hPa)可利用探空资料的露点温度和相应的饱和水汽压公式计算得到。
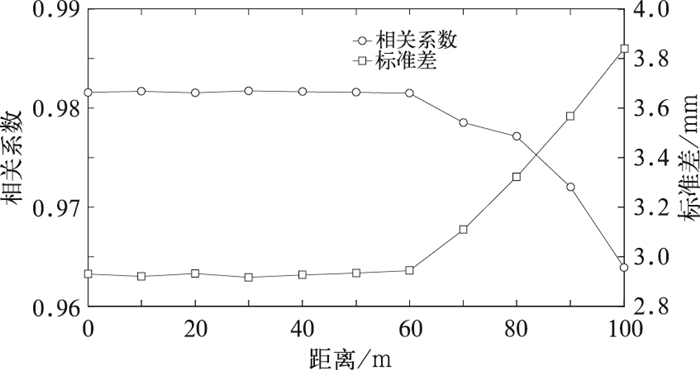
各组试验00时南昌站GPS PWV和探空PWV的相关系数和标准偏差(图 4)演变显示,在CTR试验中GPS PWV与探空PWV的相关系为0.982,标准偏差为2.92;在12个SES试验中,相关系数(标准偏差)的演变与基线相对误差和NRMS的演变相似(相反),即当南昌站的概略坐标与实际坐标偏离≥70 m后,GPS PWV和探空PWV相关系数开始逐渐下降,当概略坐标偏差为100 m时两者的相关系数下降至0.965以下;GPS PWV和探空PWV的标准偏差快速上升,当概略坐标偏差达到100 m时,两者的标准偏差超过了3.84。此外,赣州站GPS PWV与探空PWV的相关系数和标准偏差在各组试验几乎保持不变,这进一步表明了某站概略坐标的变化对其他站GPS PWV的解算没有明显的影响。
|
图 4 各组试验中南昌站GPS PWV与探空PWV的相关系数和标准差的演变情况 Fig. 4 Correlation and standard deviation between GPS PWV at Nanchang Station and sounding PWV in each test |
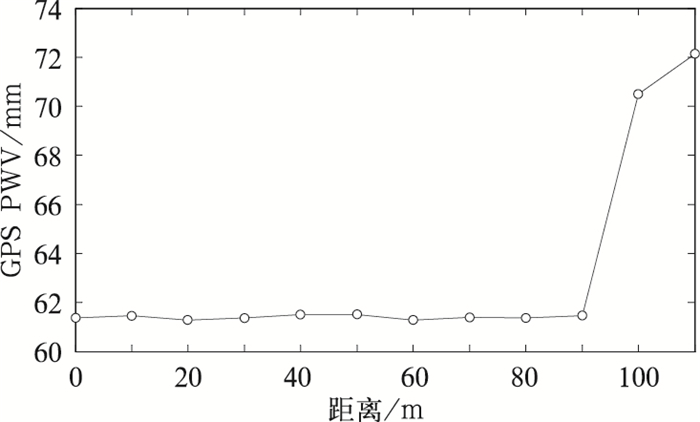
当南昌站概略坐标偏离实际坐标70 m后,不仅GPS PWV和探空PWV的相关系数和标准偏差有着明显的变化,而且南昌站GPS PWV的成功解算天数(即有GPS PWV资料生成)也有着显著的变化。在2016年第101天至第160天的60天里,在概略坐标与实际坐标偏离不超过70 m时,所有试验成功解算出南昌GPS PWV的日数均为60 d(图 3)。但在南昌站概略坐标与实际坐标偏离>70 m后,南昌GPS PWV的成功解算日数急剧下降,当偏离为80 m时,在60天中仅有40天成功解算出了南昌GPS PWV,当偏离为120 m时,60天中无一日能解算出南昌GPS PWV(图 3)。试验结果还显示(图略),各组试验中赣州站成功解算GPS PWV的日数始终保持在60天。概略坐标的变化不仅影响南昌站GPS PWV的解算是否成功,还影响GPS PWV的解算精度。图 5为各组试验2016年5月30日00时南昌站GPS PWV的演变图,从图 5可以看出,在CTR试验中南昌的GPS PWV值约为61.3 mm,与探空PWV(60.5 mm)的偏差不足1 mm,很好地反映了大气中的真实水汽。在SES试验中,南昌站的GPS PWV一直在61.3 mm附近,但当南昌站概略坐标与真实坐标偏差≥100 m后,南昌站的GPS PWV剧增至70 mm以上,明显地大于探空GPS PWV。与南昌站不同,所有试验中赣州站的GPS PWV一直维持在63.8 mm(探空为65.3 mm)附近轻微波动(振幅不超过0.4 mm)。
|
图 5 各组试验中2016年5月30日00时南昌站GPS PWV的演变情况 Fig. 5 The GPS PWV at Nanchang Station in each test at 00:00 UTC 30 May 2016 |
当概略坐标与实际坐标之间的距离大于一定值后,解算的GPS PWV不仅会出现异常高的现象,还会出现异常低的现象。如:由于江西省高安GPS监测站的搬迁(搬迁距离约为65 m),而江西省GPS/MET水汽解算系统(基于GAMIT软件)未及时更新高安站的概略坐标,解算的高安GPS PWV在2016年2月18日19时和2016年3月5日12时分别出现了一个异常大(>30 mm)的和小( < 10 mm)的孤立中心,其中心的GPS PWV值是周边地区的2倍(图 6a)和0.3倍(图 6b),这是一个明显的GSP PWV解算错误,且这个错误是由于较大的概略坐标误差造成天顶总延迟的偏强(较周边高约85 mm)和偏弱(较周边低约120 mm)所致。更新高安站概略坐标后,江西省GPS/MET水汽解算系统成功地解决了高安站GPS PWV解算错误的问题(图 7)。

|
图 6 2016年(a)2月18日19时,(b)3月5日12时未更新高安站概略坐标前江西省GPS/MET水汽解算系统解算的江西省GPS PWV (单位:mm) Fig. 6 Distribution of GPS PWV (unit: mm) solved by old approximately coordinates of Gao'an at (a) 19:00 UTC 18 February and (b) 12:00 UTC 5 March 2016 |
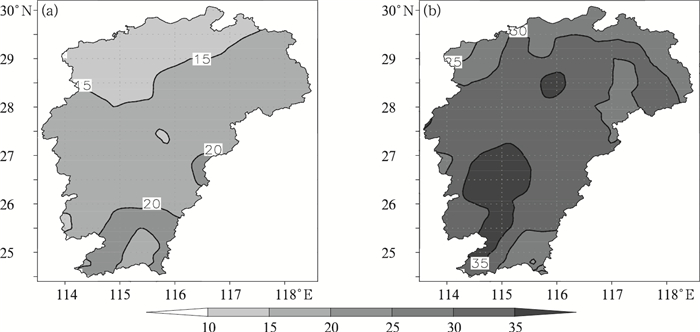
|
图 7 同图 6,但为更新高安站概略坐标后 Fig. 7 Same as Fig. 6, but for improved approximate coordinate of Gao'an Station |
在GPS水汽解算过程中,针对概略坐标精度对GPS PWV的影响,本文利用GMAIT 10.6和2016年第101天至第160天南昌站GPS观测资料,开展了1组控制性CTR(南昌站概略坐标为真实坐标)试验和12组敏感性SES(南昌站概略坐标经度以10 m等间隔逐渐向西偏移)试验,对试验结果分析发现:
(1) 当概略坐标与实际坐标的偏离在60 m以内时,概略坐标对基线的相对误差影响不大,南昌至拉萨的基线相对误差为5.7×10-9。但当偏离≥70 m以后,基线的相对误差快速增大,在偏离为90 m时,基线相对误差超过了2.0×10-8,偏离为120 m时,基线相对误差超过了2.0×10-7。
(2) 当概略坐标偏离实际坐标60 m以内时,均方根残差(NRMS)一直维持在0.215。随着概略坐标的进一步偏离,NRMS也开始逐渐增大,当概略坐标与实际坐标偏离达到120 m时,NRMS为0.24,且NRMS的变化不仅受单站概略坐标精度的影响,还与较大误差概略坐标站数的比例有关,较大误差概略坐标站数的比例占50%时,概略坐标与实际坐标偏离为120 m后,NRMS会超过0.6。
(3) 与基线相对误差和NRMS相似,在概略坐标与实际坐标的偏离≤60 m时,GPS PWV与探空PWV的相关系数和标准偏差一直维持一个固定值附近,但当偏离≥70 m以后,相关系数(标准偏差)开始下降(上升),其中标准偏差上升较快,当概略坐标偏差从60 m上升至100 m时,GPS PWV与探空PWV的标准偏差从2.92 mm上升至3.84 mm。
(4) 概略坐标的变化不仅对基线相对误差、NRMS和GPS PWV精度有明显的影响,还影响着GPS PWV能否被顺利解算。当概略坐标与实际坐标偏离≤70 m时,南昌站GPS PWV成功解算的日数均为60天,当偏离>70 m后,南昌GPS PWV成功解算的日数急剧下降,偏离为80 m时,在60天中仅有40天被成功解算,当偏离为120 m时,60天中无1天能解算出GPS PWV。
(5) 概略坐标变化对基线相对误差、GPS PWV精度以及GPS PWV能否被成功解算的影响仅限于本站,某站概略坐标的偏移不会对其他站的基线相对误差和GPS PWV精度造成明显影响。
毕研盟, 杨忠东, 李元, 2011. 应用全球定位系统、太阳光度计和探空仪探测大气水汽总量的对比分析[J]. 气象学报, 69(3): 528-533. DOI:10.11676/qxxb2011.046 |
陈敏, 范水勇, 仲跻芹, 等, 2010. 全球定位系统的可降水量资料在北京地区快速更新循环系统中的同化试验[J]. 气象学报, 68(4): 450-463. |
陈小雷, 景华, 仝美然, 等, 2007. 地基GPS遥测大气可降水量在天气分析诊断中的应用[J]. 气象, 33(6): 19-24. DOI:10.7519/j.issn.1000-0526.2007.06.003 |
楚艳丽, 郭英华, 张朝林, 等, 2007. 地基GPS水汽资料在北京"7·10"暴雨过程研究中的应用[J]. 气象, 33(12): 16-22. |
丁金才, 黄炎, 叶其欣, 等, 2004. 2002年台风Ramasun影响华东沿海期间可降水量的GPS观测和分析[J]. 大气科学, 28(4): 613-624. |
顾莹, 日下博幸, 束炯, 等, 2010. 实时GPS可降水量资料的变分同化个例研究[J]. 气象科学, 30(2): 172-178. |
郝丽萍, 邓佳, 李国平, 等, 2013. 一次西南涡持续暴雨的GPS大气水汽总量特征[J]. 应用气象学报, 24(2): 230-239. DOI:10.11898/1001-7313.20130211 |
李红莉, 万蓉, 谢有才, 2010. 利用LAPS系统同化地基GPS水汽资料的应用研究[J]. 热带气象学报, 26(6): 702-709. |
李毓麟, 刘经南, 葛茂荣, 等, 1996. 中国国家A级GPS网的数据处理和精度评估[J]. 测绘学报, 25(2): 81-86. |
梁宏, 张人禾, 刘晶淼, 2012. 青藏高原大气水汽探测误差及其成因[J]. 气象学报, 70(1): 155-164. DOI:10.11676/qxxb2012.015 |
梁伟锋, 2002. 华北GPS网GAMIT计算结果与IGs站选取的关系探讨[J]. 测绘工程, 11(4): 55-58. |
刘晶, 杨莲梅, 2017. 一次中亚低涡造成的天山北坡暴雨GPS大气水汽总量演变特征[J]. 气象, 43(6): 724-734. DOI:10.11898/1001-7313.20170608 |
刘经南, 葛茂荣, 1995. '92中国GPS会战(A级网)数据处理分析[J]. 武汉测绘科技大学学报, 20(1): 40-45. |
苗长明, 丁一汇, 郭品文, 等, 2015. 水汽输送与江南南部初夏雨季及降水变化的联系[J]. 气象学报, 73(1): 72-83. DOI:10.11676/qxxb2015.006 |
万蓉, 付志康, 李武阶, 等, 2015. 地基GPS斜路径水汽反演技术及资料应用初探[J]. 气象, 41(4): 447-455. DOI:10.7519/j.issn.1000-0526.2015.04.007 |
王佳津, 王春学, 陈朝平, 等, 2015. 基于HYSPLIT4的一次四川盆地夏季暴雨水汽路径和源地分析[J]. 气象, 41(11): 1315-1327. DOI:10.7519/j.issn.1000-0526.2015.11.002 |
王宇虹, 徐国强, 贾丽红, 等, 2015. 太行山对北京"7·21"特大暴雨的影响及水汽敏感性分析的数值研究[J]. 气象, 41(4): 389-400. DOI:10.7519/j.issn.1000-0526.2015.04.001 |
姚建群, 丁金才, 王坚捍, 等, 2005. 用GPS可降水量资料对一次大-暴雨过程的分析[J]. 气象, 31(4): 48-52. DOI:10.7519/j.issn.1000-0526.2005.04.011 |
张家国, 黄小彦, 周金莲, 等, 2013. 一次梅雨锋上中尺度气旋波引发的特大暴雨过程分析[J]. 气象学报, 71(2): 228-238. DOI:10.11676/qxxb2013.027 |
张晶, 顾松山, 楚志刚, 等, 2014. LAPS同化GPS/PWV资料在暴雨预报中的应用研究[J]. 气象, 40(1): 76-85. DOI:10.7519/j.issn.1000-0526.2014.01.009 |
张守信, 2001. 外弹道测量与卫星轨道测量基础: 第2版[M]. 北京: 国防工业出版社, 511.
|
朱丰, 徐国强, 李莉, 等, 2014. 同化青藏高原地区GPSPW数据对长江中下游地区降水预报的影响评估[J]. 大气科学, 38(1): 171-189. DOI:10.3878/j.issn.1006-9895.2013.13117 |
朱喜明, 王存良, 2004. 卫星导航定位系统中用户机概略坐标算法及仿真[J]. 飞行器测控学报, 23(3): 60-62, 94. |
邹海波, 单九生, 吴珊珊, 等, 2010. 利用GAMIT对江西省GPS可降水量的反演应用[J]. 气象与减灾研究, 33(3): 56-60. |
邹海波, 单九生, 吴珊珊, 等, 2013. GPS水汽反演方法的改善及其在台风暴雨中的应用[J]. 中山大学学报(自然科学版), 52(6): 17-25. |
Benjamin S G, Jamison B D, Moninger W R, et al, 2010. Relative short-range forecast impact from aircraft, profiler, radiosonde, VAD, GPS-PW, METAR, and mesonet observations via the RUC hourly assimilation cycle[J]. Mon Wea Rev, 138(4): 1319-1343. DOI:10.1175/2009MWR3097.1 |
Bevis M, Businger S, Herring T A, et al, 1992. GPS meteorology: remote sensing of atmospheric water vapor using the global positioning system[J]. J Geophys Res, 97(D14): 15787-15801. DOI:10.1029/92JD01517 |
Dixon T H, Gonzalez G, Lichten S M, et al, 1991. First epoch geodetic measurements with the global positioning system across the northern Caribbean plate boundary zone[J]. J Geophys Res, 96(B2): 2397-2415. DOI:10.1029/90JB02003 |
Dong Da'nan, Bock Y, 1989. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California[J]. J Geophys Res, 94(B4): 3949-3966. DOI:10.1029/JB094iB04p03949 |
Herring T A, King R W, Floyd M A, et al. 2015. GAMIT reference manual: GPS analysis at MIT[R]. Release 10.6. Cambridge: Massachusetts Institute of Technology.
|
Smith T L, Benjamin S G, Schwartz B E, et al, 2000. Using GPS-IPW in a 4-D data assimilation system[J]. Earth Planets Space, 52(11): 921-926. DOI:10.1186/BF03352306 |
 2017, Vol. 43
2017, Vol. 43 