引言

数值模式已逐渐成为提高天气预报准确率的主要工具。但是，大气的非线性和不稳定性特征所导致的预报误差增长，意味着预报模式本身的微小缺陷或初始条件的很小误差，都将不可避免地导致数值预报技巧的丧失(Lorenz，1963)，这就使得数值天气预报不可避免地具有不确定性。为了解决由于初值误差、模式误差及大气的混沌特性引起的单一数值预报的不确定性问题，Leith (1974)提出了集合预报方法，开启了数值天气预报由定量预报向概率预报转变的新纪元。

近年来以提高灾害性天气预报准确率(如台风、暴雨)为目的的中尺度短期区域集合预报研究已逐渐成为热门。中小尺度大气运动的动力机制不同于大尺度天气现象，如暴雨与中小尺度天气系统发生发展密切相关，而人们对中小尺度天气系统预报误差增长特征认识还较为有限，因此对区域数值预报新技术的研发亟待开展，在此背景下中尺度区域集合预报的研究也引起国内外许多科学家的高度重视(陈静等，2005；Stensrud and Yussouf, 2007；张涵斌等，2014；庄潇然等，2017)。

在区域集合预报研究中，如何获得合理的初值扰动是一个研究难点。目前国际上较为流行的方法有两类，一类是由全球集合预报初值扰动进行降尺度，来获得区域集合预报初值扰动(Marsigli et al，2005；Frogner et al，2006；Bowler et al，2008)。该方法主要是通过将全球集合预报初值场插值到区域模式分辨率和范围，来为区域集合产生一组初值。降尺度方法操作起来较为简单，效果也较好，已经在若干业务区域集合预报系统中得到了采用，并逐步扩展到了对流尺度集合预报中(Hohenegger et al，2008；Peralta et al，2012)；另一类为区域集合预报产生初值扰动的方法为采用区域版本的传统扰动方法(如BGM、SVs、ETKF等)，来单独为区域集合预报生成初值扰动，此类扰动方法在模式积分初期就能产生较小尺度的扰动，并能产生一定的集合离散度，提高集合预报技巧(Stensrud et al，1999；Du et al，2003；龙柯吉等，2011；Zhang et al，2015；黄红艳等，2016)。

目前，采用动力降尺度来构建区域集合初值的普遍做法是通过全球集合背景场直接动力降尺度来进行(纪永明等，2011；Weidle et al，2016)，由于全球集合分辨率的限制，许多研究均表明直接降尺度产生的扰动并不能充分包含中小尺度不确定性信息(Bowler and Mylne, 2009；Saito et al，2011；庄潇然等，2016)。在与暴雨相关的中尺度环流的发展和演变中，中小尺度波动(如重力惯性波)具有重要意义，这些波动能够显著影响包括触发局地强对流、传输能量和动量等过程(孙建华等，2013)，而随着区域模式同化技术的快速发展，高分辨率同化预报系统已能够较好地描述中小尺度、对流尺度天气现象的发生发展(范水勇等，2009；Benjamin et al，2016；王淑莉等，2015)。目前，利用充分包含中小尺度信息的区域模式高分辨率分析场来改进动力降尺度的区域集合初值，国内外鲜有报道。本文尝试将动力降尺度方法与区域模式高分辨率分析场相结合，实现“降尺度扰动”与“分析场”叠加构建区域集合初值场，以期增加动力降尺度扰动方法对中小尺度不确定性的描述能力，改善局地性天气预报技巧。通过本研究可以了解在动力降尺度扰动不变的情况下，改善初值场质量能否改善区域集合的预报效果，另外本研究结果也可为区域集合预报系统的构建提供参考。

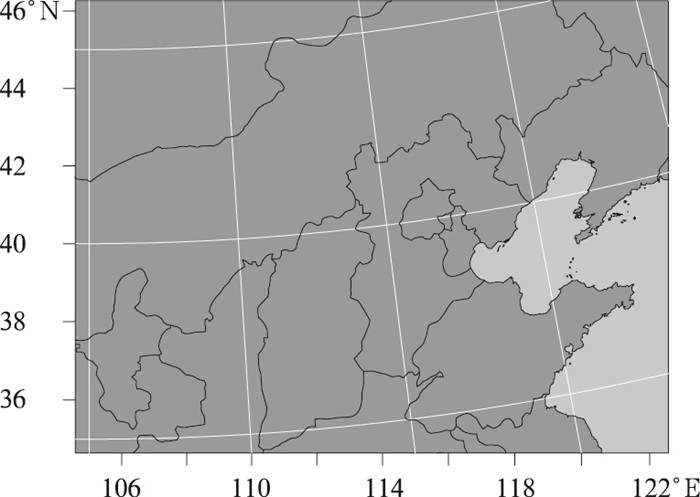
1 系统和方法介绍 1.1 系统介绍

本文试验基于中国气象局北京城市气象研究所初步发展的区域集合预报系统(WRF based regional ensemble prediction system，WRF-REPS)来开展，该系统采用WRF模式V3.5版，模式区域设置为水平分辨率6 km，模拟区域范围为35.5°~46.3°N、105.2°~122.4°E(图 1)，共274×209个格点，覆盖华北大部分区域。该系统包括一个控制预报和20个扰动成员预报共21个集合成员，系统每日从00：00 UTC开始起报，预报时效48 h。

1.2 试验方案设计

传统的动力降尺度方法，将全球集合预报直接通过区域模式进行初始化来得到区域集合的初值场，并进行模式积分，此过程并未有资料同化过程，少了区域模式分析场的参与，因此传统的动力降尺度方法虽然简便，但具有一定局限性。

目前北京市气象局业务运行的区域快速同化循环预报系统(Beijing Rapid Update Cycle System V3.0, BJ-RUC V3.0)可以提供较为精细的初始分析场，该系统运行框架为3~9 km单重嵌套，其中华北大部分地区3 km分辨率，9 km预报每日00：00和12：00 UTC冷启动两次，3 km预报使用9 km预报做边界，逐3 h进行更新的资料同化和循环预报。系统背景场采用NCEP GFS 0.5°全球预报资料，并引入GFS、EC和T639等多个全球模式背景场水汽融合。资料同化模块采用三维变分同化，同化资料包括常规地面探空、飞机报、地基GPS，以及京津冀6部雷达径向风速度和反射率因子资料。鉴于BJ-RUC分析场具有较好的质量，将其引入区域集合预报系统，与降尺度扰动进行融合，是本文研究的重点。

本文构建的区域集合预报系统首先将NCEP全球集合预报系统(Global Ensemble Forecast System，GEFS)资料初值场进行动力降尺度，获得区域模式降尺度的初值场，并与控制预报相减，提取降尺度扰动场，同时对BJ-RUC分析场(分辨率3 km)利用WPS模块进行初始化，作为区域集合的控制预报初值场，而各个集合成员的初值场则采用降尺度扰动与BJ-RUC分析场的等权线性组合，如下式：

$ I{C_i} = {A_{{\rm{RUC}}}} + \left({DOW{N_i}-DOW{N_{{\rm{ctrl}}}}} \right) $

(1)

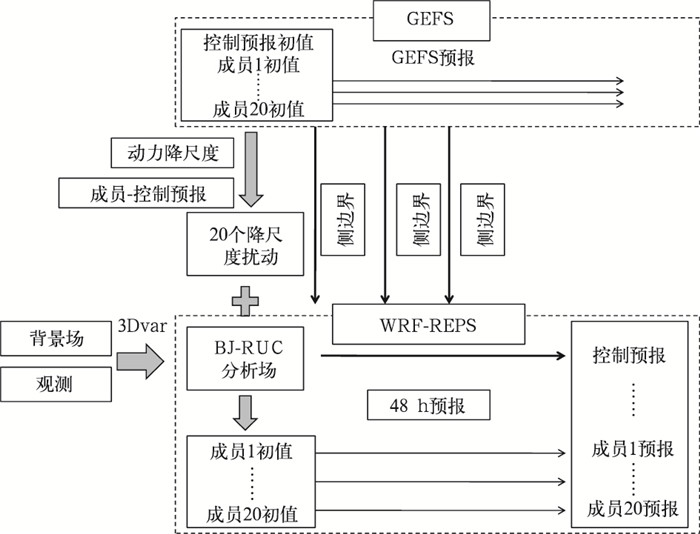
式中，IC_i代表WRF-REPS区域集合预报第i个成员的初值场，A_RUC为降尺度的BJ-RUC分析场(同时也是控制预报的初值场)，DOWN_i为GEFS全球集合第i个成员初值场降尺度后的初值场，DOWN_ctrl为GEFS全球集合控制预报降尺度后的初值场。图 2给出了区域集合试验运行流程，可以看出各成员初值为BJ-RUC分析叠加降尺度扰动场，GEFS预报场为区域集合提供侧边界条件。

为了验证此种初值处理方法的效果，本文将该方法与传统的动力降尺度方法进行对比试验，其中，传统的全球集合预报动力降尺度方法也采用GEFS资料，利用WRF模式WPS模块进行初始化获得区域集合的初值场(称为DOWN集合)；而新的区域集合初值构建方法(即首先对全球集合初值场进行降尺度，随后提取降尺度后的扰动场，再叠加BJ-RUC分析场)称为D-RUC集合，如表 1。

两组区域集合预报的分辨率以及其他各项设置均一致，为了充分对比初值构建方案的效果，集合预报试验没有进行模式扰动。本文试验时段为2015年8月连续一个月，以验证两种区域集合的统计特征。

1.3 试验资料

本文采用的背景场及侧边界条件为NCEP全球集合预报资料GEFS，集合成员20个，分辨率为1°×1°；集合预报等压面要素检验采用GFS分析场，降水检验采用国家气象信息中心整编的中国2500个台站的实况降水。

2 扰动场特征分析 2.1 扰动发展特征分析

首先对两种方法构建的扰动场发展特征进行分析。本文采用扰动总能量(different total energy，DTE) (Palmer et al，1998)来描述不同方案的扰动特征，定义某个格点的扰动总能量为：

$ \begin{array}{l} DTE = \frac{1}{2}\left[{{{u'}^2}\left({i, j, k} \right) + {{v'}^2}\left({i, j, k} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{C_p}}}{{{T_{\rm{r}}}}}{{T'}^2}\left({i, j, k} \right) \end{array} $

(2)

式中，u′、v′和T′分别为水平风场和温度的扰动，扰动值为集合成员预报和集合平均之差，c_p为干空气定压比热，T_r是参考温度，i、j、k分别是格点的水平与垂直维数。图 3为D-RUC方法和DOWN方法不同预报时效500 hPa DTE的水平分布图，起报时间为2015年8月1日12:00 UTC。可以看出，初始时刻(图 3a和3f)两种方案扰动场完全一致，均呈现出全球集合动力降尺度扰动的特征，扰动尺度较大，随着预报时效的延长(如6 h，图 3b和3g)，DOWN和D-RUC的小尺度扰动部分均有所增长，但是D-RUC小尺度扰动成分发展得更快；两种扰动均呈现出随天气流型移动的特征，24 h(图 3d和3i)两种方案的扰动形态已经表现出明显的不同，扰动的大值中心有明显差异，如DOWN集合的扰动大值中心位于模拟区域东部边界附近，扰动量级在20 J·kg^-1以上，而D-RUC集合扰动大值中心位于模拟区域北部，扰动量级也能达到20 J·kg^-1以上，说明当初始扰动一致，而初始场不一致的情况下，会导致扰动发展具有较大差异。

2.2 扰动尺度特征分析

对于一个较好的集合预报系统而言，扰动量需要包含充分的不确定性信息，不仅是大尺度信息，也包括小尺度信息。因此我们首先分析两种方法产生扰动的尺度特征。对于某个成员在某一等压面的变量，定义一个N_i×N_j的二维扰动场p(i, j)为：

$ p\left({i, j} \right) = a\left({i, j} \right)-{a_{{\rm{ctl}}}}\left({i, j} \right) $

(3)

式中，a(i, j)为某一集合成员初值场，a_ctl(i, j)为控制预报初值场。本文采用二维离散余弦变换(2-dimensional discrete cosine transform，2D-DCT) (Denis et al，2002)，来对D-RUC扰动场和DOWN扰动场进行波谱能量分析。

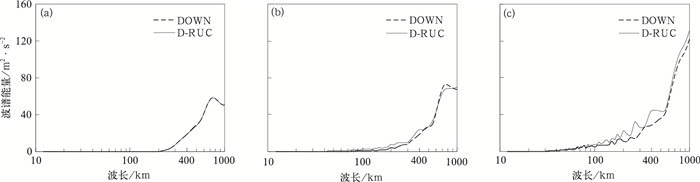
图 4给出了2015年8月1日12:00 UTC起报，预报时效为0、6和12 h的所有成员平均的500 hPa U分量风扰动波谱能量随波长的变化。从初始扰动(图 4a)波谱能量可以看出DOWN扰动和D-RUC的扰动能量完全一致，两者均在小于200 km波长范围完全没有扰动能量，这是因为这些较小尺度不能被全球模式(分辨率100 km)所分辨。对于6 h预报(图 4b)，D-RUC扰动在小尺度部分逐渐超出DOWN扰动，在大尺度扰动部分，两者能量相差不大，DOWN扰动略微占优，其波谱能量在1000 km尺度的最大值可达70 m²·s^-2。对于12 h预报结果(图 4c)，可以看出两种扰动波谱能量特征差异更为明显，其中D-RUC扰动，其小尺度(600 km以下)扰动能量有较明显增长，400 km尺度的D-RUC扰动能量值为41 m²·s^-2，而相应的DOWN扰动能量仅为27 m²·s^-2。对于较大尺度的扰动的波谱能量，两种扰动相差不大。

以上分析表明，由于D-RUC扰动是叠加到了高分辨率初值场上，随着区域模式积分，所以能够更快地激发小尺度扰动能量的发展，因此D-RUC扰动中的较小尺度扰动部分能够充分代表小尺度对流、局地性强天气的不确定性，这对于中小尺度天气现象的概率预报至关重要；而DOWN扰动则难以在较短预报时效充分代表小尺度不确定性。

2.3 扰动-误差相关性分析

较大的扰动振幅预示着较大的集合离散度，降尺度扰动中较大的扰动振幅，对于目前区域集合预报系统中离散度不够的问题是有益的，但是一个好的集合预报系统中，扰动需要能够准确地代表误差的增长特征。Toth et al (2001)及Zhu et al (2002)的研究表明一个集合预报系统能否准确捕捉不同天气形势下的预报不确定性是衡量一个集合预报系统能力的重要指标，如果真实的预报误差分布在集合扰动附近，即预报误差与集合扰动间的差异较小，说明该集合对预报误差的描述较为准确。我们将集合是否能在每个时次和空间格点上捕捉预报误差的能力称为集合扰动的准确性(Wang and Bishop, 2003)。这种集合扰动准确性的信息可以用于改善集合估计的误差概率密度函数的准确度。本节即进行集合扰动准确度试验。

该试验采用预报误差与集合平均扰动的相关性来衡量扰动的准确性。首先，计算某一层次上某一变量在所有格点上的集合平均扰动和控制预报误差，其中控制预报误差：

$ E\left({i, j} \right) = \left| {{f_{{\rm{ctl}}}}\left({i, j} \right)-a\left({i, j} \right)} \right| $

(4)

式中，f_ctl(i, j)为控制预报，a(i, j)为对应时刻的分析场，集合平均扰动：

$ P\left({i, j} \right) = \frac{{\sum\limits_{k = 1}^N {\left| {{f_k}\left({i, j} \right)-{f_{{\rm{mean}}}}\left({i, j} \right)} \right|} }}{N} $

(5)

式中，f_k(i, j)为第k成员的预报，f_mean(i, j)为集合平均预报，N为集合成员数。

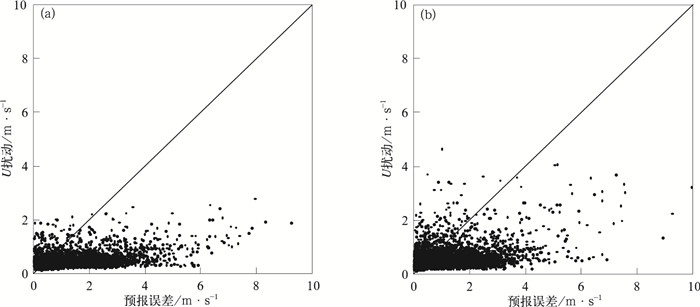
对于所有格点样本，可以绘制以预报误差为横坐标、以集合平均扰动为纵坐标的散点图。图 5给出了2015年8月1日12:00 UTC起报，6 h预报时效的500 hPa U分量风的集合平均扰动与预报误差的散点图。可以看出DOWN方案(图 5a)多数散点分布在对角线以下，呈现出预报误差较大而扰动较小的状态，集合扰动的量级最大也不超过3 m·s^-1，说明DOWN集合扰动明显更低估了预报误差；对于D-RUC方案(图 5b)，集合扰动与预报误差的量级对应得更好，在对角线附近分布得更均匀，其中某些点的集合扰动的量级可以达到4 m·s^-1左右。以上分析表明D-RUC扰动比DOWN扰动能够更好地识别预报场中哪些位置预报误差较大，而哪些位置预报误差较小。

以上研究表明，虽然初始时刻扰动一致，但是D-RUC方法和DOWN方法在经过短时效积分后，D-RUC集合扰动的小尺度分量发展更快，并且其扰动形态更能与预报误差相匹配，更好地代表预报不确定性。

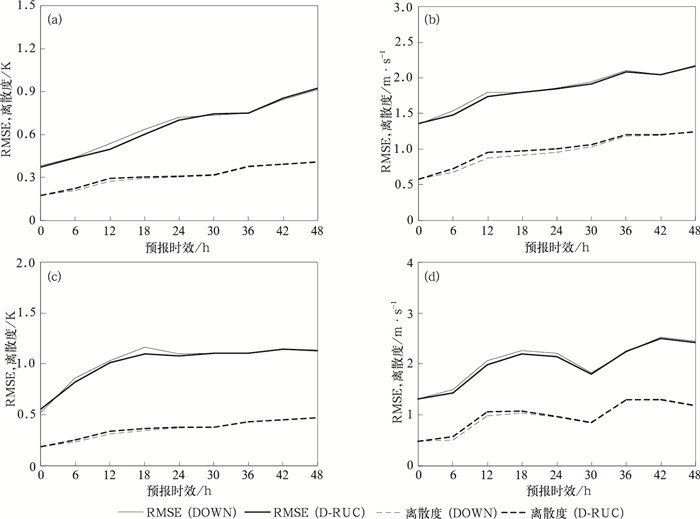
3 集合预报检验 3.1 集合离散度和均方根误差

衡量一个集合预报系统好坏的标准之一是集合离散度(ensemble spread)能否与集合平均均方根误差(RMSE)大致相当。图 6给出了2015年8月1—30日30天48 h预报时效的集合离散度和RMSE，要素分别为U850、T850、U500和T500。通过对比可以发现，对于前18 h预报时效，D-RUC方法的集合离散度均略高于DOWN方法，如12 h预报时效U500(图 6b)D-RUC的离散度可以达到0.95 m·s^-1，而DOWN方法的离散度可以达到0.87 m·s^-1，随着预报时效的延长，两种方案的集合离散度比较接近。对于短预报时效RMSE，D-RUC方案要小于DOWN方案，如18 h预报时效的T850(图 6c)DOWN的均方根误差可以达到1.16 K，而D-RUC方法的离散度可以达到1.09 K。18 h预报时效之后，两种方案集合平均均方根误差相差不大。据此可以初步认为，D-RUC方法能够有效提高短时效的集合离散度，减少预报误差。

3.2 CRPS评分

为了进一步了解D-RUC方法对区域集合预报的改进效果，计算出两种方案连续等级概率评分(continuous ranked probability score，CRPS)。CRPS是近年来国外常用的集合预报概率评分(Hersbach，2000)，该方法能够定量比较预报累计分布概率与观测累计分布概率距离差异。CRPS评分值是负定向的，值越高表示集合预报系统的概率预报性能越差。

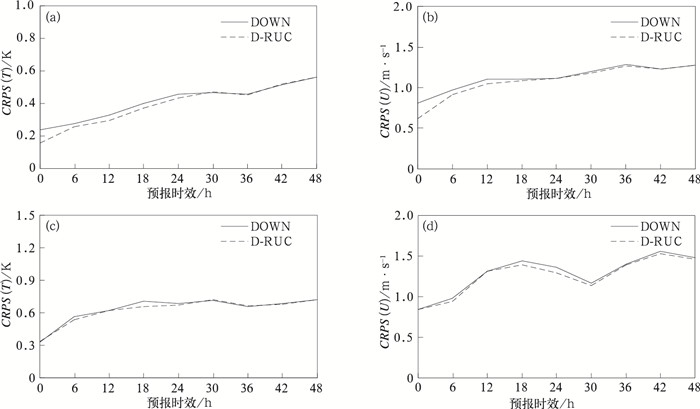
图 7给出了D-RUC和DOWN集合T500、U500、T850和U850的CRPS评分。分析得出，在前18 h预报时效，D-RUC集合的CRPS评分要低于DOWN集合，随着预报时效的延长，两者差异逐渐变小，CRPS评分很接近，说明D-RUC集合在短预报时效能够提供更为准确的概率预报技巧。对其他等压面变量的检验(图略)也可以支持这个结论。

3.3 Talagrand分布

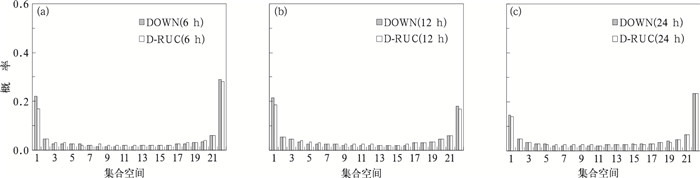
Talagrand分布(Hamill et al，2000)是评估集合预报系统可靠性的一个指标，其评估了观测落在各集合成员间或者集合成员之外的频率。一个较为可靠的集合预报系统其Talagrand分布应该较为平缓。“U”型分布表明系统离散度不足，“J”型或者“L”型分布表明系统存在预报偏差。图 8给出了850 hPa U分量风6、12和24 h预报时效的Talagrand分布。总体上两个集合均表现出离散度不足，相对而言，6和12 h的D-RUC集合比DOWN集合分布更平缓，表明观测更易于分布在D-RUC集合内；对于24 h预报时效，两种集合的Talagrand分布相差不大。

通过以上连续一个月的集合预报检验结果可以看出，D-RUC集合在短预报时效内比DOWN集合有明显的优势，说明即使在扰动一致的情况下，初始场质量的改善也能影响到集合概率评分效果，这种改善对短时效概率预报的作用尤为显著。

4 降水个例分析

为了检验两种动力降尺度方法的降水预报效果，研究了2015年夏季一次典型的强降水个例。D-RUC集合和DOWN集合均从2015年8月7日00：00 UTC起报。

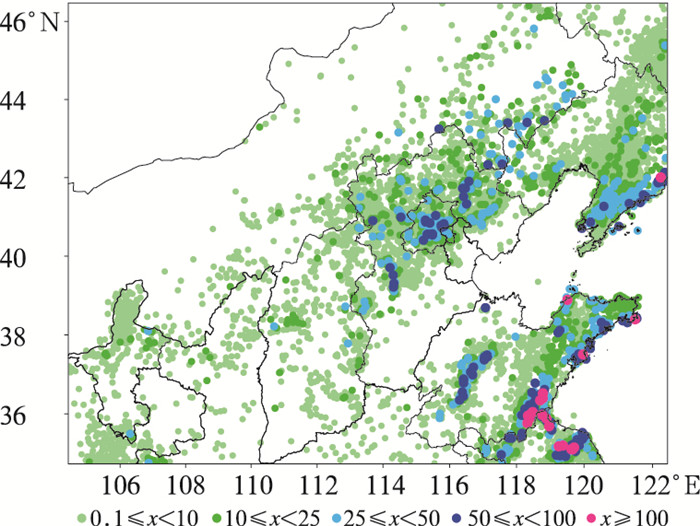
图 9给出了集合模拟区域观测的2015年7日00：00 UTC至8日00：00 UTC的24 h累计降水。可以看出该降水个例的范围较大，覆盖了华北大部分地区，主要有两条雨带，其中河北的北部、北京的雨带呈东北—西南向分布，山东的东部和南部降水量级也较大，可达50 mm以上。

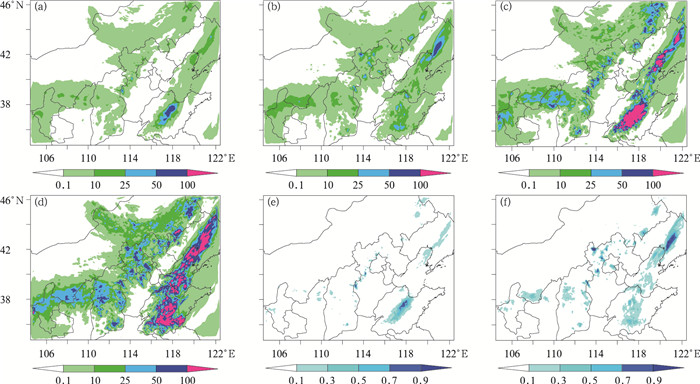
图 10给出了DOWN和D-RUC集合的24 h累计降水集合平均预报、最大降水预报以及大于25 mm降水概率预报。首先对于集合平均预报，DOWN集合降水分布(图 10a)与实况相比有所偏差，其中，对北京和山东南部的强降水中心，DOWN集合平均预报均没有给出很好的模拟，存在明显的漏报，说明大部分成员均没有较好地报出这两个中心；D-RUC集合平均(图 10b)预报有了较好地改善，在北京地区和山东南部地区均有明显的降水，如山东南部降水量级可达25 mm以上。集合最大降水预报结果可以明显看出，DOWN集合最大降水预报(图 10c)在山东中部和西南部量级较大，可达100 mm以上，实况在此地区也存在明显降水，可以给出一定的指示信号，但是对北京地区和山东南部降水中心依然没有报出；D-RUC集合最大降水预报(图 10d)显示，在北京地区、山东中部和南部均有强降水中心，北京地区降水量级可达50 mm以上，山东中部和南部降水可达100 mm以上，与实况对应较好。对于大于25 mm降水概率预报，对于DOWN集合(图 10e)，降水概率较大区域依然在山东中部和北部，其他地区给出的指示信号很小，相比较而言，D-RUC集合预报(图 10f)，大雨预报的较高概率的位置和范围更加接近实况的强降水中心，如北京地区和山东南部降水概率大雨概率均超过了50%，与实况观测对应更好。

相对作用特征(relative operation curve，ROC)(段明铿等, 2009)是信号探测理论运用到集合预报的二分类检验方法，对某一格点或站点，通过预报和真实值判断一个事件发生与否，得到预报准确、空报、漏报，预报正确为X，漏报为Y，空报为Z，正确否定为W。从而得出信号探测理论中两个主要的量：假警报率Z/(Z+W)和命中率X/(X+Y)。将命中率和假警报率在同一坐标系中描绘出来，就得到了ROC曲线。AROC为ROC曲线与x轴围成的面积，可以用来表示系统的预报技巧。ROC曲线越接近左上角，系统的预报能力对事件的预报技巧就越好；越接近于对角线，预报技巧就越差，完美的预报AROC=1，没有技巧的预报AROC=0.5。

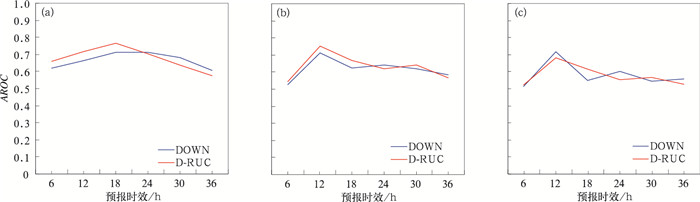
图 11给出的是DOWN集合和D-RUC集合逐6 h累计降水AROC评分随预报时效的变化。如图所示，对于>0.1 mm和>4 mm量级的降水，在前24 h预报时效，D-RUC集合AROC评分均要好于DOWN集合，24 h预报时效之后，两种集合降水评分相差不大；对于>13 mm降水(图略)，两种集合方法不同预报时效的降水评分各有优劣。

以上降水个例分析表明，D-RUC集合能够提供更好的降水概率预报结果，改善降水的落区预报。与集合预报检验结果类似，D-RUC集合相对于DOWN集合的优势主要体现在短预报时效内，其中对于小雨、中雨量级降水预报的改进尤为显著。以上结果的主要原因是当集合扰动与分析场相结合来构建集合成员时，可以使每个成员均包含经过资料同化的高质量分析场的成分，因此这些成员对降水落区，尤其是对局地对流性降水的位置把握较好。

5 结论与讨论

本文基于WRF模式，利用GEFS全球集合预报资料驱动构建了区域集合预报系统，并试验了两种动力降尺度初值处理方法，一种是直接对全球集合初值场进行动力降尺度，另一种是提取全球集合动力降尺度扰动场，并与BJ-RUC初始分析场叠加构建区域集合的初值场。进行了一个月的批量试验，对扰动特征进行了分析，对概率预报效果进行了检验，并对试验时段内的典型降水个例模拟效果进行了分析，得出如下结论：

(1) 两种集合的初值扰动场一致，随着预报时效的延长扰动量级均有较为明显的增长，但与全球集合初值场动力降尺度的扰动相比，与BJ-RUC分析场叠加的降尺度扰动增长具有明显差异，其中，与分析场叠加后的降尺度扰动的小尺度扰动分量增长要明显快于全球集合直接降尺度扰动，而大尺度扰动分量的增长两者相当，说明与高分辨率分析场叠加可以促进动力降尺度扰动的中小尺度扰动分量的增长。

(2) 集合预报扰动准确性检验结果显示，全球集合直接降尺度方案的集合扰动明显低估了预报误差，在预报误差较大的位置扰动较小，而与分析场叠加后的降尺度扰动，能够更好地识别预报场中哪些位置预报误差较大，而哪些位置预报误差较小。

(3) 集合预报检验结果表明，降尺度扰动叠加分析场的集合方法比全球集合直接降尺度方法在短预报时效具有更高的离散度，概率预报技巧也稍高，在较长预报时效，两种方法预报技巧十分接近。加优异，可以有效改善初值场直接降尺度方法的漏报问题，提高降水概率预报技巧，其中对短预报时效的小雨、中雨量级预报改进尤为明显。

本文试验结果说明降尺度扰动叠加区域模式高分辨率分析场可以作为有效地构建区域集合预报系统的技术手段，能有效改善全球集合初值场直接降尺度的不足，尤其是对短预报时效预报效果的改进较为明显。这也从一个侧面说明提高区域集合预报的效果不仅需要较好的扰动来充分代表预报的不确定性，也可以结合高质量的分析场来为集合成员获得优质的初值。本文为了纯粹对比两种初值处理方法，并没有引入模式扰动，为了提高较长预报时效的概率预报效果，今后仍需模式扰动的参与(袁月等，2016)；另外，动力降尺度扰动虽然可以给出较好的背景场动力学不确定性特征，但不能体现分析场中观测的不确定性，因此引入观测扰动也是今后的工作重点。