2. 安徽省气象科学研究所,安徽省大气科学与卫星遥感重点实验室,合肥 230031
2. Anhui Meteorological Science Research Institute, Anhui Laboratory of Atmospheric Science and Satellite Remote Sensing, Hefei 230031
西太平洋副热带高压(简称副高)是影响东亚天气气候最主要的大气环流系统之一,中国的地理位置决定了受副高的影响很大,其位置和强度变化对我国气候异常有重要影响(陶诗言和卫捷,2006)。副高的季节内变化决定我国东部雨带的几次向北推移,而其年际变化决定我国东部旱涝的出现(吴瑶和杜良敏,2016;蒋薇等,2016)。近年来的异常气候事件,如1998年和2016年夏季长江流域的特大洪涝,2013年江淮江南持续高温酷暑,均与副高活动有着密切关系(高辉等,2017;袁媛等,2017)。因此,副高位置和强度的正确预测对我国气候预测有着直接的指示意义。
国内外学者对副高预测已有大量研究,取得长足进步。副高预测方法可以分为数理统计预测方法和动力学预测方法。数理统计预测方法大致分为两类:一类是单纯的统计预测模型,如多层递阶预报方法(张恩恕等,1984;1989)、前传式神经网络算法(张韧,2001)、小波分解和自适应神经模糊推理系统相结合(张韧,2001;张韧等,2004;董兆俊和张韧,2004)、小波分解和最小二乘支持向量机相结合(刘科峰等,2007;2009)、自组织网络与广义回归网络耦合(王彦磊等,2008)、相空间重构(张韧等,2007)、遗传优化(洪梅等,2013),模糊系统(洪梅等,2006;2015)等等。一类是物理因子统计预测模型,主要是基于前期海温和环流指数的多元回归预测模型(艾悦秀和陈兴芳,2000;贾亚俊等,2015),相对单纯的统计预测模型,所选预报因子是建立在科学分析的基础上,具有相对明确的物理含义。
第二种是动力学预测方法。任宏利等(2005)发展了一个描述副高脊面变化的动力模型,该模型对月副高脊面有一定模拟能力。邹立维等(2009)用可预报性指数证实了副高具有较高的可预报性。洪梅等(2007)重构了副高指数的非线性动力模型。随着数值模式广泛应用,马德贞等(1999)评估了T106和ECMWF数值预报产品对副高的预报能力,认为ECMWF对1~6 d副高进退趋势预报能力较强。杨杰等(2012)基于动力-统计相似预报原理,建立副高模式预测订正方案,其结果较模式显示出较高的预测水平。刘芸芸等(2014)评估认为经气候态订正后,CMIP5多数模式有能力刻画副高指数的历史时间变化。付炳秀等(2016)评估了CFSv2对夏季副高的逐日预测能力,认为1~7 d副高预报准确率较高。Li et al(2012;2014;2016)认为副高季度预测水平呈现年代际变化,目前海气耦合模式可以相当好地预测副高异常,即使是在没有明显ENSO信号时副高的预测准确率依然比较高。总体来看,随着动力模式预测水平不断提高,基于动力模式的副高预测已经成为主要发展方向,也成为各大气候业务中心的主流工具。
目前国家气候中心第二代月动力延伸预测模式业务系统(DERF2.0)已经投入业务应用。该模式对候、旬、月气候变率均体现出一定预测能力,其对降水、气温、环流等要素的预测技巧较第一代模式有明显提升,在我国短期气候预测特别是月尺度气候预测中发挥着重要作用(吴统文等,2013;何慧根等,2014)。以往对该模式的评估着重于要素和基本环流,缺乏对于关键环流因子如副高的检验评估,因此有必要在应用时对模式的副高预测性能开展评估,以便更多地了解模式性能,发挥其优势,为短期气候预测提供参考。本文基于DERF2.0模式的历史回报资料,结合NCEP/NCAR再分析资料和副高监测指数,利用时间相关系数、标准化均方根误差、距平符号一致率和泰勒图分析等方法综合评估DERF2.0模式对月尺度副高的预测性能,为合理利用模式进行副高预测和改进模式性能提供科学依据,以期提高短期气候预测业务的准确率。
1 资料和方法 1.1 副高指数简介本文所关注的副高采用《西太平洋副热带高压监测业务规定》中的标准。副高是指出现在西北太平洋上的暖性副热带高压系统,其范围大小以500 hPa位势高度场的588 dagpm等值线所包围的区域来表示。副高各指数定义如下:副高面积是表征西太副高范围大小的指标,即在10°~50°N、110°~180°E范围内,500 hPa高度场上所有≥588 dagpm的格点所围成的面积总和。副高强度是表征西太副高强弱的指标,即在10°~50°N、110°~180°E范围内,500 hPa高度场上所有≥588 dagpm的格点所围成的面积与该格点高度值减去587 dagpm差值的乘积的总和。副高脊线位置是表征西太副高南北位置的指标,即在10°~50°N、110°~150°E范围内,500 hPa高度场上588 dagpm等值线所包围的西太副高体内纬向风切变线(即u=0,
环流资料包括1983—2015年国家气候中心DERF2.0模式历史回报资料和NCEP/NCAR再分析资料。DERF2.0模式采用滞后平均方案进行逐日滚动预报,预报时间长度53 d。模式回报的月平均资料为一个月中日预报数据的算术平均值。DERF2.0模式回报资料和NCEP/NCAR再分析资料分辨率分别为1.0°×1.0°和2.5°×2.5°。为保证两者的一致性,使用双线性插值将模式回报资料插值为与再分析资料相同分辨率。
1.3 检验评估方法检验评估指标包括标准化均方根误差(SRMSE)、时间相关系数(Tcc)和距平符号一致率(Pc)。标准化均方根误差(SRMSE)为观测值与预测值的均方根误差与观测值标准差的比值(施晓晖等,2006),用来衡量预测值和观测值之间的偏差。时间相关系数(Tcc)为观测时间序列和预测时间序列的相关系数,用来衡量两者线性关系的密切程度。距平符号一致率(Pc)为预测距平和观测距平符号一致的次数与总次数的比值,用来衡量预测和观测距平趋势演变的一致程度。
为全面、直观地评估副高观测与预测的一致性,引入泰勒图分析方法。泰勒图是由预测与观测的相关系数、相对标准差及其标准化均方根误差组成的极坐标图(Taylor, 2001),其距原点的距离表示模式相对于观测的标准差,方位角的余弦代表模式与观测的相关系数,与参考点(REF)的距离反映模式相对于观测的均方根误差。
2 模式对副高关键区环流的预测能力评估在定量描述副高强度和位置等变化特征的副高指数中,面积指数、强度指数和西伸脊点指数都与500 hPa位势高度场的5880 gpm等值线密切相关,而脊线指数则由500 hPa等压面上纬向风u=0等值线的纬度位置所决定(刘芸芸等,2012)。因此,首先从气候态和年际变率两个方面检验评估DERF2.0模式对西太平洋500 hPa高度场和纬向风场的预测能力。
2.1 气候态DERF2.0模式可以超前20多天预测下个月的环流场。考虑到不同超前起报时间的模式预报性能有所不同,选择超前0、5、10和15 d起报的模式预测结果进行分析。
图 1和图 2是1983—2015年多年平均的观测值(NCEP/NCAR再分析资料)和DERF2.0模式超前0、5、10、15 d起报1—12月500 hPa高度场上5880 gpm等值线分布图和u=0等值线分布图。以超前0 d起报作为模式预测代表,可以看出DERF2.0模式预测的5880 gpm等值线空间分布及其范围与观测在多数月份较为接近。两者的差异主要表现为模式预测的5880 gpm所包围的范围比观测偏大,高度场强度偏强。有些月份差异较大,如1—5月。1和2月观测场上没有找到闭合的5880 gpm等值线,而模式预测场上存在明显闭合的5880 gpm等值线。3、4和5月模式预测的5880 gpm所包围的范围明显偏大,高度场强度偏强。表明模式对气候平均态上5880 gpm等值线的空间分布和范围具有较强的预测能力,但具有偏大偏强的系统偏差。超前0、5、10、15 d起报的模式预测与观测对比来看,超前起报天数越长,模式预测系统性偏大偏强的偏差就越大。
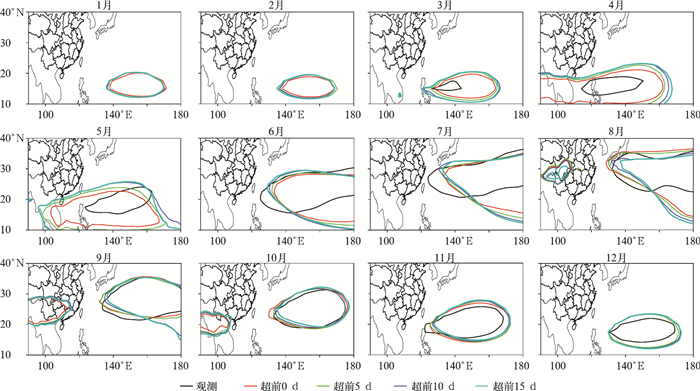
|
图 1 1983—2015年多年平均的观测(NCEP/NCAR再分析资料)和DERF2.0模式超前0、5、10、15 d起报的1—12月500 hPa位势高度场上5880 gpm等值线分布 Fig. 1 Distribution of monthly geopotential height 5880 gpm isoline averaged from 1983 to 2015 at 500 hPa for the observation (NCEP/NCAR reanalysis) and the DERF2.0 model prediction when the lead time is 0, 5, 10 and 15 days |
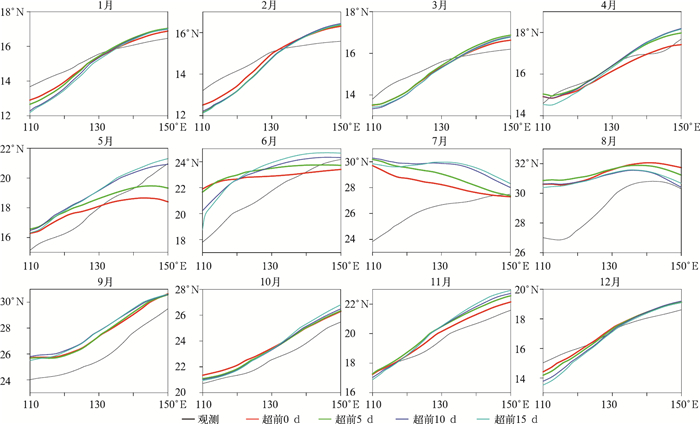
|
图 2 同图 1,但为纬向风u=0等值线分布 Fig. 2 Same as Fig. 1, but for distribution of monthly zonal wind u=0 isoline |
模式预测的纬向风u=0等值线位置与观测在多数月份较为一致(图 2)。表明模式对多数月份500 hPa等压面上纬向风切变线有较强的预测能力。部分月份模式预测的纬向风u=0等值线位置与观测差异较为明显,如6—9月,在110°~140°E模式预测的纬向风切变线位置较观测明显偏北。多数月份模式对纬向风切变线的预测偏差会随着超前起报天数延长而增大。
2.2 年际变率图 3为1983—2015年模式超前0、5、10、15 d起报的副高关键区(10°~45°N、110°~180°E)500 hPa高度场和纬向风场与观测值的泰勒图,可以看出模式对于不同超前天数起报的高度场和纬向风场的预测性能存在明显差异,多数月份模式超前0 d起报的高度场和纬向风场标准化均方根误差最小,时间相关系数最大,预测性能相对最好,而超前15 d起报的模式预测性能相对最差。表明模式对高度场和纬向风场的预测性能依赖于超前起报时间,超前起报时间越临近预报时段,时间相关系数越大,标准化均方根误差越小,模式预测性能越好。

|
图 3 1983—2015年DERF2.0模式预测的西太平洋1—12月500 hPa高度场(a)和纬向风场(b)与观测场的泰勒图 (图中REF代表观测,各模式到原点的半径代表相对于观测的标准差,模式在图中方位角的余弦代表模式与观测的相关系数,模式到REF的距离代表相对于观测的均方根误差。H500和U500分别表示500 hPa高度场和纬向风场,0、5、10、15分别表示超前0、5、10、15 d起报的模式预测,下同) Fig. 3 Taylor diagrams of monthly geopotential height (a) and zonal wind (b) from 1983 to 2015 at 500 hPa over the western pacific for the observation and the DERF2.0 model prediction (REF indicates observation; the radial distance of the model code point from the origin is the standardized deviation ratio of the models relative to observation; the correlation coefficient of spatial pattern between the model prediction and the observation is shown by the cosine of the azimuthal angle of model code point, and their root mean square error is given by the distance of model code point from the REF; H500 and U500 indicate geopotential height and the zonal wind at 500 hPa, respectively; 0, 5, 10 and 15 indicate model prediction when the lead time is 0, 5, 10 and 15 days, respectively. The same below) |
从模式超前0 d起报的环流预测检验来看,模式对1—12月高度场预测与观测的时间相关系数为0.57~0.89,均可以达到0.05的显著性水平检验,除5月外均大于0.6。模式对纬向风场预测与观测的时间相关系数在0.41~0.83,均可以达到0.05的显著性水平检验。表明模式对副高关键区高度场和纬向风场预测和观测时间演变的一致性较好。对比来看,模式对高度场的预测性能要明显优于对纬向风场的预测。
模式对高度场预测的标准化均方根误差在0.5~0.86,均小于1。对纬向风场预测的标准化均方根误差在0.59~1.14,除5月外均小于1。根据标准化均方根误差的定义,如果其值大于1.0,表示预测与观测的均方根误差超过了观测的标准差,即误差较大,反之,如果其值小于1.0,则表示两者的均方根误差小于观测的标准差,即误差较小。因此上述分析结果表明,模式对高度场和纬向风场的预测误差较小。对比来看,模式对高度场的预测误差要明显小于对纬向风场的预测。
模式对高度场预测相对观测的标准差范围在0.68~1.09,除7月外均小于1,对纬向风场预测相对观测的标准差范围在0.68~1.28,除2、5、6和7月外均小于1。表明多数月份模式对高度场和纬向风场预测的年际变率振幅要比观测小。
分月来看,模式对高度场预测性能最佳的是9月,相关系数最大(0.89),标准化均方根误差最小(0.5)。最差的是5月,相关系数最小(0.57),标准化均方根误差最大(0.86)。模式对纬向风场预测性能最佳的是6和7月,相关系数最大(0.82),标准化均方根误差最小(0.6),最差的是5月,相关系数最小(0.66),标准化均方根误差最大(1.14)。
3 模式对副高指数的预测能力评估主要从气候态、年际变率、距平符号一致率三个方面来检验评估模式对副高指数的预测性能。
3.1 气候态首先评估模式对副高指数气候态的预测能力。图 4是模式超前0~20 d预测和观测1983—2015年多年平均月副高指数。可以看出与观测相比,模式超前0~20 d预测的副高面积、强度和脊线明显偏大,西伸脊点明显偏小。以超前0 d起报为例,预测与观测相比,副高面积偏大34,强度偏大23,脊线偏大0.49°N,西伸脊点偏小8°E。表明模式对副高气候平均态的预测较观测存在系统性偏差,表现为副高面积偏大,强度偏强,脊线偏北,西伸脊点偏西。
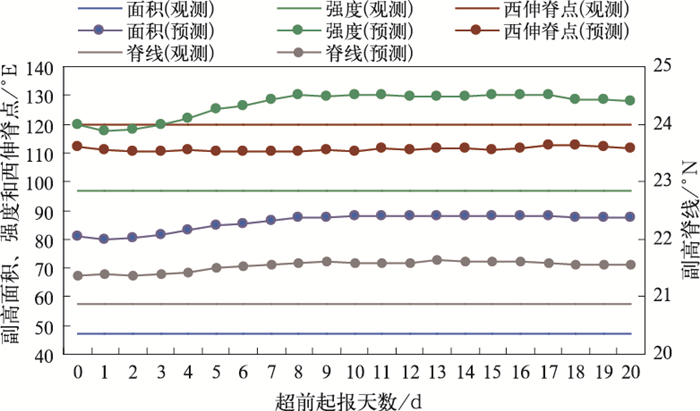
|
图 4 DERF2.0模式超前0~20 d预测和观测的1983—2015年多年平均月副高面积、副高强度、副高脊线和副高西伸脊点 Fig. 4 The WPSH area index, intensity index, ridge line index, western boundary index averaged from 1983 to 2015 at 500 hPa for the observation and the model prediction when the lead time is from 0 to 20 days |
从不同起报时间来看,随着超前起报时间延长,副高面积、强度和脊线模式预测的气候态越大,意味着模式对气候态的预测较观测的偏差越大。表明模式对副高气候平均态的预测偏差会随着超前起报时间延长而不断增长。
为了了解分月情况,图 5给出1983—2015年多年平均超前0、5、10、15 d起报的模式预测和观测的1—12月副高指数,可以看出模式较为准确地预测了副高的年循环信息,冬季各月副高面积小,强度弱,脊线南,夏季各月副高面积大、强度强、脊线北。模式预测不足主要表现为副高指数预测存在明显的系统性偏差。与观测相比,模式预测的副高面积和强度存在系统性偏大偏强,脊线8—12月明显偏北,西伸脊点4—5月和8—10月明显偏西。
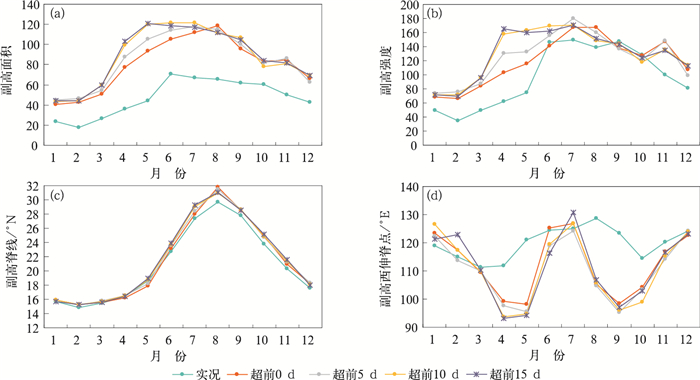
|
图 5 1983—2015年多年平均超前0、5、10、15 d起报的模式预测和观测的1—12月副高面积(a)、副高强度(b)、副高脊线(c)和副高西伸脊点(d) Fig. 5 The monthly WPSH area index (a), intensity index (b), ridge line index (c), west ridge point index (d) averaged from 1983 to 2015 for the observation and the model prediction when the lead time is 0, 5, 10 and 15 days |
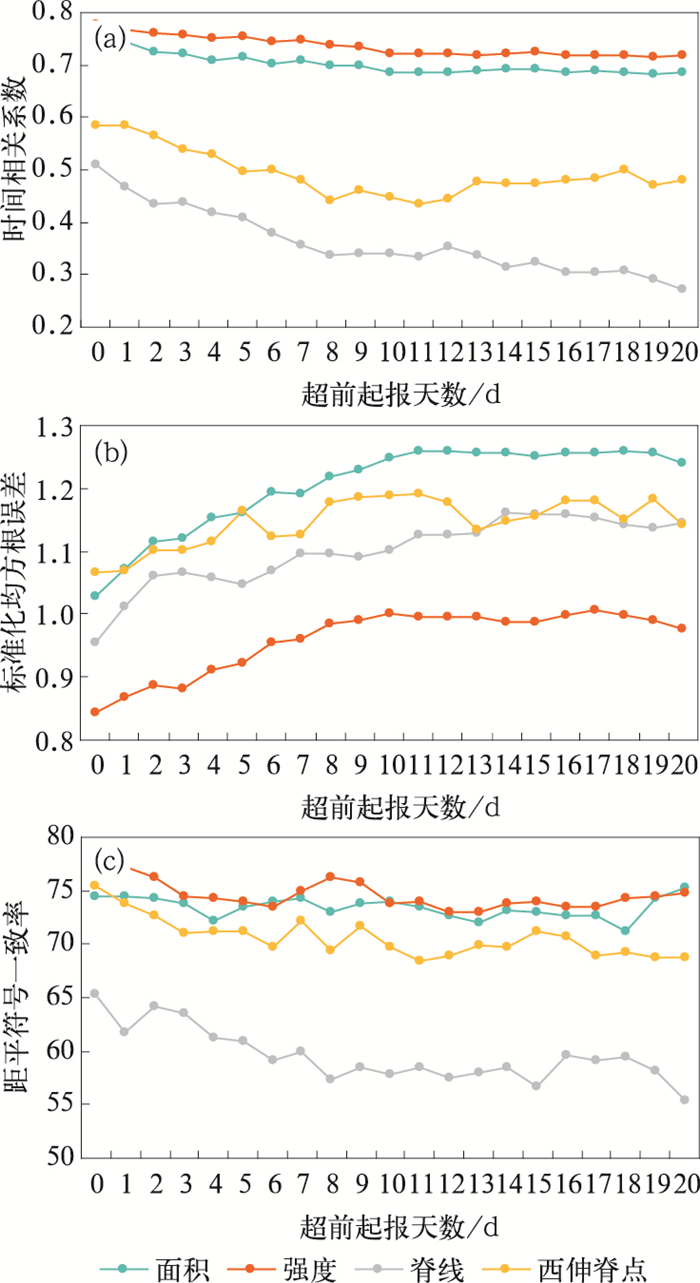
为了分析模式对副高指数的预测性能与超前起报时间的关系,给出DERF2.0模式不同超前起报天数的副高指数预测与观测的时间相关关系、标准化均方根误差和距平符号一致率(图 6)。可以看出随着超前天数的缩短,起报时间的临近,模式预测副高指数与观测的时间相关系数越大,标准化均方根误差越小,距平符号一致率越大。模式超前0 d起报的副高面积、强度、脊线和西伸脊点标准化均方根误差分别为1.03、0.84、0.96、1.07,与观测的相关系数分别为0.76、0.78、0.51、0.58,距平符号一致率分别为74.5、78.3、65.4、75.5分。与超前5 d起报相比,副高面积、强度、脊线和西伸脊点的标准化均方根误差分别降低了0.13、0.08、0.09、0.1,而相关系数分别增大了0.05、0.02、0.1、0.09,距平符号一致率分别提高了1、4.3、4.4、4.3分。表明模式对副高的预测性能依赖于超前起报时间,随着起报时间临近预报时段,均方根误差减小,时间相关关系和距平符号一致率增大,预测性能整体呈上升趋势。实际预测业务中,需及时采用更新的预测对副高进行滚动订正。
|
图 6 DERF2.0模式不同超前起报时间对未来一个月副高指数预测与观测的时间相关系数(a)、标准化均方根误差(b)和距平符号一致率(c) Fig. 6 Time correlation coefficient (a), normalized root mean square error (b) and anomaly sign consistency rate (c) of the coming monthly WPSH index between the observation and the model prediction when the lead time is from 0 to 20 days |
超前0 d起报的副高预测评估来看,预测和观测的时间相关关系从大到小为:副高强度,面积,西伸脊点和脊线,其中强度和面积超过0.6。表明模式对副高强度和面积具有较高的预测性能,西伸脊点次之,脊线相对较差。标准差均方根误差从小到大为:副高强度、脊线、面积和西伸脊点,其中强度和脊线小于1。表明模式对副高强度和脊线的预测误差较小,而对面积和西伸脊点的预测误差较大。从距平符号一致率(Pc)来看,超前0~20 d起报的副高面积和强度均超过70分;其次是西伸脊点,超前0~5 d也超过70分;脊线相对较差,只有超前0~5 d超过60分。表明模式对副高强度和面积的距平符号预测性能最佳,而对脊线预测较差。综合认为:副高强度的模式预测性能最佳,其次是面积,脊线相对较差。
考虑到每月气候预测时需要判断副高的趋势,较高的相关系数和距平符号一致率意味着应用该模式判断副高趋势时具有一定参考价值,但模式对于副高脊线和西伸脊点的预测性能仍偏弱,尤其是对于脊线位置这一影响中国雨带分布的关键因子预测能力仍较差,还有很大改进空间。此外综合来看模式超前起报越短的副高预测性能相对更高,尽可能选用起报超前时间短的预测,这对每月气候预测会商和滚动订正具有积极意义。
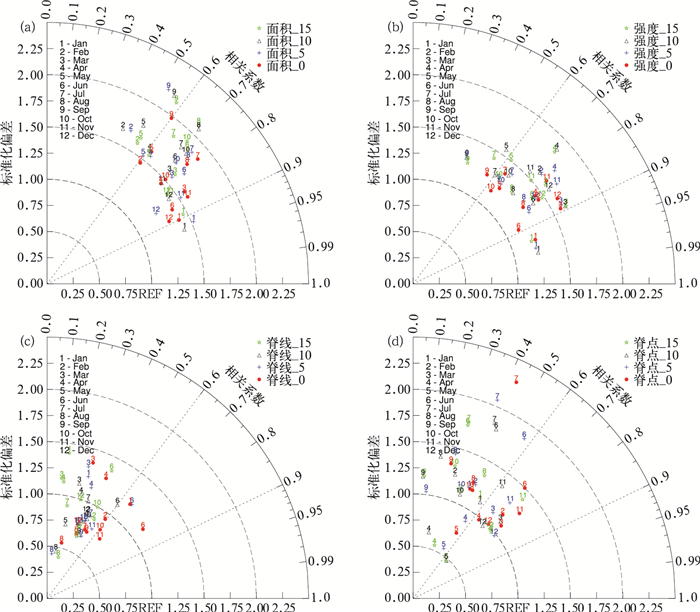
图 7为1983—2015年模式预测与观测1—12月副高指数的泰勒图。重点分析超前0 d起报的模式预测。从模式预测与观测的时间相关系数(Tcc)来看,副高面积Tcc为0.6~0.9,均达到0.05显著性水平检验,1和12月较大,9月最小;强度Tcc为0.57~0.94,均达到0.05显著性水平检验,除9月外均大于0.5,1月最大,9月最小;脊线Tcc为0.25~0.83,6月最大,3和8月最小,除3和8月外均达到0.05显著性水平检验;西伸脊点Tcc为0.27~0.78,11和3月最大,9月最小,除9月外均达到0.05显著性水平检验。
|
图 7 同图 3,但为(a)副高面积,(b)强度,(c)脊线,(d)西伸脊点的泰勒图 Fig. 7 Same as Fig. 3, but for (a) area index, (b) intensity index, (c) ridge line index and (d) west ridge point index of WPSH |
从标准化均方根误差(SRMSE)来看,副高面积SRMSE为0.63~1.6,12和1月最小,9月最大;强度SRMSE为0.52~1.08,6月最小,9月最大;脊线SRMSE为0.66~1.41,6月最小,3月最大;西伸脊点SRMSE为0.71~2.07,3月最小,7月最大。
综合时间相关系数和标准化均方根误差分析认为,模式对副高指数有较好的预测性能,副高强度最佳,面积其次,西伸脊点和脊线相对较差。不同月份的预测性能存在明显差异,副高面积1和12月最佳,9月最差;强度1月最佳,9月最差;脊线6月最佳,3月最差;西伸脊点3月最佳,7月最差。
从相对观测值的标准差来看,副高面积和强度相对标准差均大于1;西伸脊点5月小于1,4月约等于1,其余多数月份均大于1;而脊线1月、3月、4月和6月大于1,其余多数月份均小于1。表明模式高估了副高面积、强度和西伸脊点的年际变率振幅,而低估了多数月份副高脊线的年际变率振幅。
3.3 距平符号一致率气候预测业务中,最为关注的是副高的距平趋势,因此距平符号一致率(Pc)评估尤其重要。为了衡量模式预测距平符号一致率好坏,以业务常用的持续性预测(用上个月副高距平值直接预测下个月副高距平趋势)作为对比,模式预测评分高于持续性预测时,模式预测具有较高的业务参考价值。月副高面积、强度、脊线和西伸脊点持续性预测Pc评分分别为72.5、75.3、58.4和71分。
对比图 6,可以看出模式对副高指数的预测性能高低与持续性预测性能高低的特征基本一致:副高强度预测性能最佳,其次是面积,脊线相对最差。副高面积除超前4和13 d起报外的Pc评分均大于持续性预测,副高强度超前0~2和8~9 d,脊线超前0~7、9、11、14、16~18 d,西伸脊点超前0~5、7、9、15 d起报的Pc评分大于持续性预测。综合认为,模式对副高面积超前0~20 d、强度超前0~2 d、西伸脊点超前0~5 d、脊线超前0~7 d起报对未来一个月的预测性能优于持续性预测,在月预测中可以重点参考。
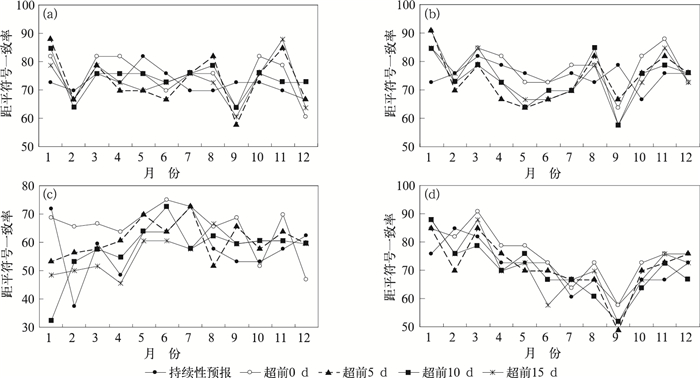
分月来看,各月模式预测和持续性预测的Pc评分存在明显差异(图 8)。从持续性预测的Pc评分来看,副高面积除12月外、强度除10月外均大于70分;西伸脊点1—6月和12月均大于70分;脊线只有1月、5—7月和12月大于60分。模式超前0天起报的预测中,副高面积有7个月,强度有8个月、脊线有8个月、西伸脊点有9个月的Pc评分超过持续性预测。部分月份模式预测Pc评分高于持续性预测的幅度超过了10%,如1、4、10和11月副高面积预测Pc超过了13%;1、10和11月强度预测分别超过了25%、23%和16%;2—6月、8—9月和11月等8个月脊线预测超过了10%,其中2、4和9月超过了75%、31%、29%;1、3和11月西伸脊点超过了12%、11%和14%。相反的是,模式对2和9月副高面积、强度和西伸脊线的预测评分Pc要明显低于持续性预测,且9月Pc评分为12月中最低。
|
图 8 DERF2.0模式预测与持续性预测1—12月副高面积(a)、强度(b)、脊线(c)和西伸脊点(d)距平符号一致率对比图 Fig. 8 Anomaly sign consistency rate of WPSH area index (a), intensity index (b), ridge line index (c), west ridge point index (d) for persistence forecast and the DERF2.0 model prediction |
随着超前天数的延长,模式对副高的预测性能超过持续性预测的月份数不断下降。超前15 d起报的模式预测中,副高面积只有6个月,强度有5个月、脊线有5个月、西伸脊点有7个月的Pc评分高于持续性预测。
气候预测业务中,副高趋势是持续还是转折十分重要。表 1给出了不同副高距平趋势演变下模式超前0天起报的副高预测评分。可见模式对副高距平趋势持续的预测有相当高的准确率,副高面积、强度和西伸脊点预测评分Pc均在80分以上,脊线达到76.8分,但对副高指数距平趋势转折的预测性能较差,各个副高指数预测评分Pc基本在50~60分。
|
|
表 1 不同趋势演变和ENSO事件下模式超前0 d起报对未来一个月的副高预测距平符号一致率 Table 1 Anomaly sign consistency rate of the coming monthly WPSH index under different trend evolutions and ENSO event conditions for DERF2.0 model prediction when the lead time is 0 day |
ENSO是影响副高活动的重要因素,也是气候预测业务常用的副高预测依据。根据《厄尔尼诺+拉尼娜事件监测业务规定》中的ENSO事件表,1983—2015年共有10次厄尔尼诺事件和8次拉尼娜事件,厄尔尼诺事件、拉尼娜事件、ENSO正常状态的样本数分别为110、88和198个月,严格按照ENSO事件开始和结束月份划分影响时段,统计了不同ENSO事件下模式超前0天起报的副高预测评分Pc(表 1)。可以看出有厄尔尼诺事件或者拉尼娜事件发生时,副高指数预测评分Pc普遍高于没有ENSO信号时的预测,尤其是脊线和西伸脊点。即使在没有ENSO信号时,模式对副高指数的预测依然具有较好的预测性能,副高强度预测评分Pc接近80分,面积和西伸脊点在70分以上,脊线64分,均高于持续性预测。另外,有拉尼娜事件发生时副高指数预测评分Pc高于有厄尔尼诺事件发生时的预测,尤其是强度和西伸脊点。
4 结论基于DERF2.0模式1983—2015年回报数据,结合NCEP/NCAR再分析资料和副高监测指数,利用多种方法综合评估了模式对月尺度副高的预测性能。
(1) 模式能够预测出气候平均态上588 dagpm等值线的空间分布及强度和纬向风切变位置,但有偏大偏强的系统偏差。模式对高度场年际变率的预测性能好于纬向风场。
(2) 模式较为准确地预测了副高气候态的年循环信息,但有明显的系统偏差,副高面积相对观测偏大,强度偏强,脊线偏北,西伸脊点偏西,这种系统偏差随着超前起报时间的延长而不断增大,是模式预测性能随着起报时间下降的重要原因。模式对副高年际变率预测性能较好,其中强度最佳,面积其次,脊线相对较差;脊线预测仍有很大改进空间。
(3) 模式对副高的预测性能依赖于超前起报时间,随着起报时间的临近,系统偏差和均方根误差减小,相关关系和距平符号一致率增大,预测性能整体呈上升趋势。业务中需及时采用更新的预测对副高进行滚动订正。
(4) 模式对副高面积超前0~20 d、强度超前0~2 d、西伸脊点超前0~5 d、脊线超前0~7 d起报对未来一个月的预测性能优于持续性预测,业务中可以重点参考。
(5) 模式对副高趋势持续的预测有相当高的准确率,但对副高趋势转折的预测性能较差。有ENSO信号时副高预测性能优于没有ENSO信号时的预测,尤其是脊线和西伸脊点。即使在没有ENSO信号时,副高预测性能依然较好,优于持续性预测。
本文着重于从应用角度评估了DERF2.0模式对副高的预测能力,没有对其误差来源进行分析,也没有进行模式预测误差订正。下一步在副高预测性能评估基础上,开展有针对性的副高预测误差订正研究,进一步提高副高的预测准确率。
艾悦秀, 陈兴芳, 2000. 夏季副高与海温的相互关系及副高预测[J]. 热带气象学报, 16(1): 1-8. |
付炳秀, 王同美, 韦翠, 等, 2016. 基于CFSv2对夏季西太平洋副高逐日预测能力的检验评估[J]. 广东气象, 38(2): 15-19. |
董兆俊, 张韧, 2004. 基于小波分解的西太平洋副热带高压模糊推理预测[J]. 热带气象学报, 20(4): 419-425. |
高辉, 袁媛, 洪洁莉, 等, 2017. 2016年汛期气候预测效果评述及主要先兆信号与应用[J]. 气象, 43(4): 486-494. DOI:10.7519/j.issn.1000-0526.2017.04.011 |
何慧根, 李巧萍, 吴统文, 等, 2014. 月动力延伸预测模式业务系统DERF2.0对中国气温和降水的预测性能评估[J]. 大气科学, 38(5): 950-964. |
洪梅, 陈希, 张韧, 等, 2015. 基于模糊系统的西太平洋副热带高压异常年份的影响因子检测分析和动力预报模型反演[J]. 气象学报, 73(2): 355-367. DOI:10.11676/qxxb2015.017 |
洪梅, 张韧, 何金海, 2006. 基于动力统计模型重构的副热带高压中长期预报[J]. 气象学报, 64(6): 780-789. DOI:10.11676/qxxb2006.074 |
洪梅, 张韧, 刘科峰, 2013. 基于遗传优化的西太平洋副高异常活动年份的动力预报模型反演[J]. 物理学报, 62(7): 84-92. |
洪梅, 张韧, 吴国雄, 等, 2007. 用遗传算法重构副热带高压特征指数的非线性动力模型[J]. 大气科学, 31(2): 346-352. |
贾亚俊, 胡轶佳, 钟中, 等, 2015. 夏季西太平洋副热带高压指数的统计预测模型[J]. 高原气象, 34(5): 1369-1378. DOI:10.7522/j.issn.1000-0534.2014.00079 |
蒋薇, 张祖强, 刘芸芸, 2016. 21世纪以来西南地区干季降水与西太平洋副热带高压年代际变化的关系[J]. 气象, 42(11): 1335-1341. |
刘科峰, 张韧, 洪梅, 等, 2009. 基于最小二乘支持向量机的副热带高压预测模型[J]. 应用气象学报, 20(3): 354-359. DOI:10.11898/1001-7313.20090312 |
刘科峰, 张韧, 于鹏, 等, 2007. 基于小波分解和最小二乘支持向量机的西太平洋副高预测模型[J]. 热带气象学报, 23(5): 491-496. |
刘芸芸, 李维京, 艾秀, 等, 2012. 月尺度西太平洋副热带高压指数的重建与应用[J]. 应用气象学报, 23(4): 414-423. DOI:10.11898/1001-7313.20120404 |
刘芸芸, 李维京, 左金清, 等, 2014. CMIP5模式对西太平洋副热带高压的模拟和预估[J]. 气象学报, 72(2): 277-290. DOI:10.11676/qxxb2014.025 |
马德贞, 毛恒青, 鲍媛媛, 等, 1999. 盛夏数值预报模式对副高预报性能检验及其释用[J]. 气象, 25(3): 50-54. |
任宏利, 张培群, 郭秉荣, 等, 2005. 预报副高脊面变化的动力模型及其简化数值试验[J]. 大气科学, 29(1): 71-78. |
施晓晖, 徐祥德, 谢立安, 2006. NCEP/NCAR再分析风速、表面气温距平在中国区域气候变化研究中的可信度分析[J]. 气象学报, 64(6): 709-722. DOI:10.11676/qxxb2006.068 |
陶诗言, 卫捷, 2006. 再论夏季西太平洋副热带高压的西伸北跳[J]. 应用气象学报, 17(5): 513-525. DOI:10.11898/1001-7313.20060509 |
王彦磊, 滕军, 张韧, 等, 2008. 自组织网络与广义回归网络耦合的副热带高压指数预测[J]. 热带气象学报, 24(5): 475-482. |
吴统文, 宋连春, 刘向文, 等, 2013. 国家气候中心短期气候预测模式系统业务化进展[J]. 应用气象学报, 24(5): 533-543. DOI:10.11898/1001-7313.20130503 |
吴瑶, 杜良敏, 2016. 副高脊线的月内振荡对汉江上游秋汛的影响[J]. 气象, 42(11): 1379-1386. DOI:10.7519/j.issn.1000-0526.2016.11.010 |
杨杰, 封国林, 赵俊虎, 等, 2012. 夏季西太平洋副热带高压的客观定量化预测及其对汛期降水的指示[J]. 气象学报, 70(5): 1032-1044. DOI:10.11676/qxxb2012.086 |
袁媛, 高辉, 柳艳菊, 2017. 2016年夏季我国东部降水异常特征及成因简析[J]. 气象, 43(1): 115-121. DOI:10.7519/j.issn.1000-0526.2017.01.013 |
张韧, 2001. 基于前传式网络逼近的太平洋副热带高压活动的诊断预测[J]. 大气科学, 25(5): 650-660. |
张韧, 董兆俊, 陈奕德, 等, 2004. 西太平洋副高形态指数的分解重构与集成预测[J]. 地球科学进展, 19(4): 572-576. |
张韧, 王辉赞, 刘科峰, 等, 2007. 基于相空间重构的西太平洋副高指数的动力随机性与复杂性[J]. 南京气象学院学报, 30(6): 723-729. |
张恩恕, 毛玉英, 韩志刚, 等, 1984. 西太平洋副热带高压夏季特征量的多层递阶长期预报模型——副高特征量长期预报(一)[J]. 高原气象, 3(2): 51-56. |
张恩恕, 汤兵勇, 韩志刚, 1989. 西太平洋夏季副高积分多层递阶长期预报模型[J]. 气象科学研究院院刊, 4(1): 69-74. |
邹立维, 周天军, 吴波, 等, 2009. GAMIL CliPAS试验对夏季西太平洋副热带高压的预测[J]. 大气科学, 33(5): 959-970. |
Li Chaofan, Lu Riyu, Dong Buwen, 2012. Predictability of the western North Pacific summer climate demonstrated by the coupled models of ENSEMBLES[J]. Climate Dyn, 39(1/2): 329-346. |
Li Chaofan, Lu Riyu, Dong Buwen, 2014. Predictability of the western North Pacific summer climate associated with different ENSO phases by ENSEMBLES multi-model seasonal forecasts[J]. Climate Dyn, 43(7/8): 1829-1845. |
Li Chaofan, Lu Riyu, Dong Buwen, 2016. Interdecadal changes on the seasonal prediction of the western North Pacific summer climate around the late 1970s and early 1990s[J]. Climate Dyn, 46(7/8): 2435-2448. |
Taylor K E, 2001. Summarizing multiple aspects of model performance in a single diagram[J]. J Geophys Res Atmos, 106(D7): 7183-7192. DOI:10.1029/2000JD900719 |
 2017, Vol. 43
2017, Vol. 43 