引言

降水粒子形状是重要的降水微物理特征之一，研究表明(刘西川等，2013；Beard et al, 2010)，随雨滴尺度的增加，雨滴形状由球形向近似椭球形转变，致使不同偏振状态的电磁波具有不同的散射特性，进一步影响电磁波在雨中的传播和衰减特性；这一特征已在双偏振雷达定量估测降水(张亚萍等, 2013)、微波链路衰减订正和卫星反演降水等领域得到广泛的应用(Michaelides, 2008; 温龙等，2015；廖荣伟等，2015；潘旸等，2011)。

Pruppacher and Pitte (1971)通过考虑液体静压力和空气动压力在雨滴表面任意一点的平衡得到PP模型，即直径<2 mm的雨滴基本保持球形，>2 mm的雨滴顶部呈圆滑、底部由平坦状向凹状过渡；Beard and Chuang (1987)在PP模型的基础上考虑雨滴的表面张力，利用拉普拉斯压力平衡方程计算得到BC模型，其大雨滴相对于PP模型底部无凹状；Pruppacher and Klett (1997)指出雨滴形状主要受液体静压力、空气动压力、表面张力、电场力、雨滴内部环流决定；Bhalwankar et al (2015)利用在雨滴风洞实验中添加不同方向和强度的电场，指出随着水平电场强度的增加雨滴平均轴比随之减小；说明雨滴形状在不同的外力影响下具有不同的形状。Thurai and Bringi (2007)和Thurai et al (2010)利用2DVD在亚拉巴马(Alabama)的观测资料进行分析，发现在层状云性降水的雨滴形状与Thurai模型相符，但对流性降水的雨滴形状在3.5~3.75 mm较Thurai模型(Thurai et al, 2007)具有更圆的形状，进一步说明在不同的大气环境下雨滴呈现不同的形状；目前，国内外测量雨滴形状以高速线阵CCD扫描为主如2DVD (Kruger and Krajewski, 2002)，但当受水平风影响时，雨滴可能产生水平方向位移，改变雨滴真实形状。

基于面阵CCD传感器的降水微物理特征测量仪(PMCS)(刘西川等，2014a)可在同一时间完整呈现雨滴形状，并经过多次外场观测试验(刘西川等，2014b)验证了该仪器具有测量降水粒子形状、下落末速度、尺度及其谱分布的能力。本文根据PMCS在外场观测中捕获的雨滴数据，分析了异常图像形成原因、处理方法和数字雨滴图像矢量化方法，进一步分析不同尺度粒子的形状和轴比分布特征，为更多的降水微物理特征研究奠定基础。

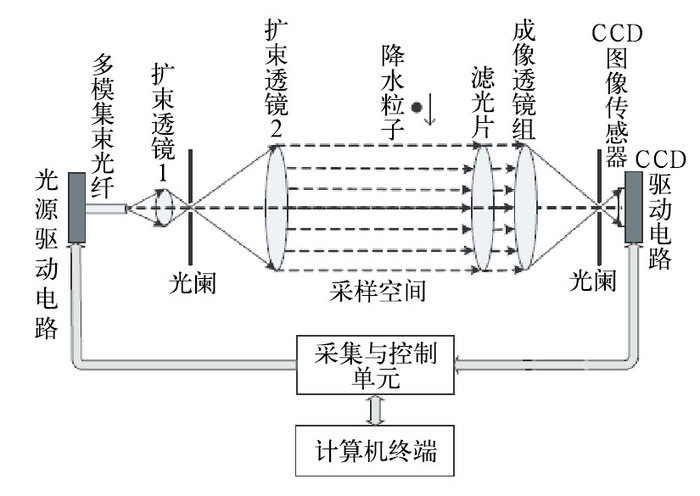
1 PMCS的简介

降水微物理特征测量仪(Liu et al, 2014)又称面阵CCD雨滴谱仪(precipitation micro-physical characteristics sensor，PMCS)，由光学单元、成像单元、采集与控制单元、数据处理单元和防护单元构成，如图 1所示，光学单元由平行光源、扩束透镜组和成像透镜组组成，其作用是为粒子成像提供均匀、一致和稳定的背景场；成像单元由面阵CCD图像传感器及其驱动电路组成，其作用是对穿过采样区域的降水粒子进行快速曝光成像；采集和控制单元由数字信号处理器DSP芯片、复杂可编程逻辑器件CPLD、复位电路、时钟电路、总线接口及存储芯片等配套电路组成，主要实现大数据量图像的高速、实时采集、处理与传输等功能；数据处理单元由终端计算机和相关应用软件组成，主要实现图像数据的进一步处理、降水特征量的提取。

PMCS以平行光作为成像背景场，消除了景深效应对粒子成像的影响。当降水粒子穿过采样空间时，PMCS通过对光源和快门的精密配合实现单帧图像内对该粒子进行两次曝光，然后根据采集的粒子图像得到其大小与形状，并根据粒子先后两次曝光的位置与间隔时间计算水平和垂直速度，详细参数指标见表 1。在PMCS投入实地观测之前，已进行了考虑环境光强与背景光场平行性的小球定标试验(Shu et al, 2015)，确定了基于粒子像元面积的自适应阈值图像处理方法，对捕获的粒子图像依次采用中值滤波、线性空间滤波、腐蚀等图像处理方法进行处理，并根据粒子像元面积与二值化阈值之间函数关系进行二值化，最终可获得较为准确的二值化数值雨滴图像。

2 资料获取与异常图像处理

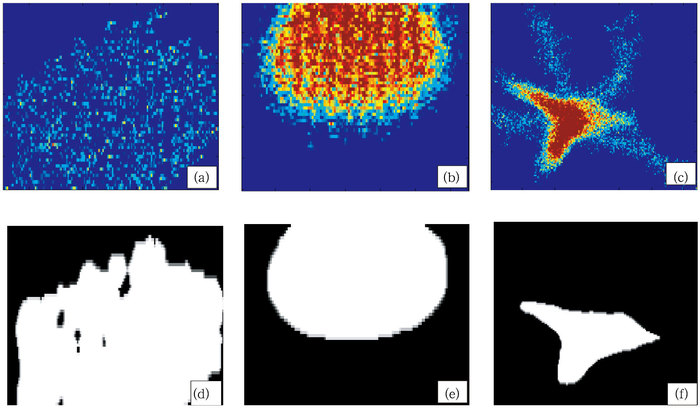
本文利用2015年6月16日PMCS在南京地区所捕获的降水粒子进行分析。此次降水过程最大降水强度为96.15 mm·h^-1，持续时间为16 h，累积捕获的粒子数为351773个，是一次典型的对流性降水过程。但是，PMCS捕获的粒子不全是完整的降水粒子，这里面还包括异常粒子，如图 2a~2c所示，主要可分为三类，第一类为水迹和镜头污染所致，由于PMCS长期置于户外，空气中的灰尘就会附着于镜头上污染镜头，加上在雨天，空气中的细小雨滴与污染物混合形成污染水迹；第二类为雨滴处于采样空间边缘所致，由于单帧图像时间和曝光时间及间隔均是一定的，曝光时，无法保证所有粒子均在采样空间之中；第三类为空气中的小昆虫所致，无论在晴天还是雨天，小昆虫均有可能飞过采样空间被仪器所捕获。

虽然异常值无法完全在硬件上进行避免，但具有明显的特征，第一类粒子具有离散的像元，第二类粒子有部分像元置于图像边界，第三类粒子具有复杂二值化图像边缘，现定义空隙度(P)，二值化边缘像元数(E)，以及粒子形状参数(F)作为剔除异常值的特征量，表达式如下：

$P = \frac{{{P_r}}}{{{P_b}}},{\rm{ }}E = \sum b{w_{{\rm{edge}}}},{\rm{ }}F = \frac{{{L^2}}}{{4\pi S}}$

(1)

式中，P_b代表二值图像元值为1所对应的像元数，P_r代表二值图像值为1对应的原始图像区域中像元亮度值>5对应的像元数；bw_edge表示二值图像边缘像元值为1的像素总和；F代表形状参数，L表示二值图像边缘对应的像元数，S表示二值图像所有像元的总和。

由于上述特征量均为统计量，其对应的取值范围需要进行统计分析，因此针对粒子图像数据，采用手动筛选方式，每间隔0.2 mm选出100张有效的雨滴图像，并计算其相应的特征量。其中P, E的筛选结果如图 3a, 3b所示，筛选图像的P大多在0.9以上，E在1个像元以内即可得到P≥0.9，E≤1的判别函数。利用此函数对所有粒子图像进行处理，获得的粒子图像依然存在异常F值如图 3c所示，可根据3σ准则进行剔除，现以0.2 mm为间隔分别求取不同直径范围内F平均值。其F整体平均为1.699，标准差平均为0.076，平均值拟合曲线为F=-0.5347D^-0.427+2.0983，以3倍标准差为界得到的上下边界如图 3c所示，可以看出筛选的有效雨滴图像的F值均在该范围内。综上所述，可确定异常值判别函数如下，利用该函数对所有观测样本进行处理，最终获得的有效雨滴图像数为234093个。

$\left\{ \begin{array}{l} P \ge 0.9,{\rm{ }}E \le 1,{\rm{ }}{F_{up}} \le F \le {F_{{\rm{down}}}}\\ {F_{{\rm{up}}}} = - 0.5347{D^{ - 0.427}} + 2.0983 + 0.25\\ {F_{{\rm{down}}}} = - 0.5347{D^{ - 0.427}} + 2.0983 - 0.25 \end{array} \right.$

(2)

3 基于Akima插值的数字雨滴图像矢量化方法 3.1 雨滴图像矢量化算法设计

PMCS所捕获的雨滴图像，通过图像处理算法，最终得到是雨滴的二值图，受数值图像分辨率的限制，其边缘呈锯齿状，形如图 4中的阴影部分，而真实形状(红色实线)被掩盖在数值图像的二值化边缘图像(深灰色部分)之中，需要采用适当的矢量化方法才能提取出雨滴的真实形状。从图 4中可以看出，数值雨滴边缘图的拐点可以作为矢量化的特征点，尤其是内角点以及外角点具有与真实形状一致的变化趋势，如果分别以内外角点为基础将其连续化并取两者平均，可进一步达到矢量化雨滴数值图像的目的。

目前，离散点连续化的方法主要有拟合和插值法，但无论利用何种方法在直角坐标系下进行连续化，均需要分象限进行，导致矢量化形状在不同象限的交接处容易产生畸变。因此，将连续化过程转换到极坐标系下进行。即以(0, 0) 为中心的原始坐标(x, y)，经x_ρ=x-x_c, y_ρ=y-y_c的平移到以二值图像重心(x_c, y_c)为中心的直角坐标系下，然后根据式(3) 进行极坐标变换，得到粒子图像在以(x_c, y_c)为中心的极坐标值；最后依据不同的插值方法对提取点数据进行插值，利用坐标逆变换将极坐标系下的粒子转换至笛卡尔坐标系得到反演雨滴形状。

$\begin{array}{*{20}{l}} {\quad \quad \quad \quad \rho = \sqrt {x_\rho ^2 + y_\rho ^2} }\\ {\theta = \left\{ {\begin{array}{*{20}{l}} {{\rm{arctan}}(\left| {\frac{{{y_\rho }}}{{{x_\rho }}}} \right|),{x_\rho } > 0,{y_\rho } > 0}\\ {{\rm{arctan}}(\left| {\frac{{{x_\rho }}}{{{y_\rho }}}} \right|) + \frac{\pi }{2},{x_\rho }{\rm{ < }}0,{y_\rho } > 0}\\ {{\rm{arctan}}(\left| {\frac{{{y_\rho }}}{{{x_\rho }}}} \right|) + \pi ,{x_\rho }{\rm{ < }}0,{y_\rho }{\rm{ < }}0}\\ {{\rm{arctan}}(\left| {\frac{{{x_\rho }}}{{{y_\rho }}}} \right|) + \frac{{3\pi }}{2},{x_\rho } > 0,{y_\rho }{\rm{ < }}0} \end{array}} \right.} \end{array}$

(3)

经过上述讨论，可以确定实测雨滴形状处理流程(图 5)，利用经图像处理之后的雨滴二值图，采用四连通准则提取雨滴边缘，采用角点检测算法提取内外角点，然后在极坐标系下利用连续化方法分别获得内外角点的连续函数，得到内接和外接光滑形状，最后取其内外接形状的平均形状，经直角坐标变换得到雨滴的真实形状，但角点连续化方法需要进一步讨论。

3.2 角点连续化方法

角点连续化方法主要有拟合和插值法，但由于拟合法需要首先对拟合形状进行假设，有可能破坏真实雨滴形状，因此以讨论使用插值方法为主。目前，常用插值法有线性插值，Spline插值(梁雄贵，2010)，Akima插值(Akima, 1970)等。线性插值利用相邻两点的信息，根据过两点的直线进行插值；Spline插值利用分片多项式函数，考虑所有点对它的影响求解得到满足任何两个相邻点之间的三次多项式；Akima插值在任何两个相邻点之间内插时，需要考虑与此两点相近邻的四个已知点的值，并以任意一个点具有连续的一阶导数为条件，利用三次多项式逼近完成插值。由于雨滴形状随着直径的增加，形状由球形向非球形过渡，无法预知真实形状，所以采用模拟数字图像粒子对插值方法进行检验。

首先利用Thurai模型[式(4)，其中D_eq表示雨滴等效直径，x，y表示对应笛卡尔坐标系坐标]产生模拟雨滴形状；然后，根据面阵CCD图像分辨率按比例进行数值化转换，得到的模拟雨滴的数字化二值图像形如图 4；其次，利用该二值图采用四连通准则提取二值图像的边缘，并根据提取的边缘分别提取内角点和外角点；最后分别对内角点和外角点进行插值得到其对应的外接形状，取两者的平均形状作为反演雨滴形状。

$\left\{ \begin{array}{l} x = {c_1}\sqrt {1 - {{(\frac{y}{{{c_2}}})}^2}} \left[ {{\rm{co}}{{\rm{s}}^{ - 1}}(\frac{y}{{{c_3}{c_2}}})} \right]{\rm{ }}\left[ {{c_4}{{(\frac{{{y_4}}}{{{c_2}}})}^2} + 1} \right],\\ \quad {D_{{\rm{eq}}}} \ge 1.5{\rm{ mm}}\\ {x^2} + {y^2} = D_{{\rm{eq}}}^2,{\rm{ }}{D_{eq}} < 1.5{\rm{ mm}} \end{array} \right.$

(4)

式中

$\left\{ \begin{array}{l} {c_1} = \frac{1}{\pi }(0.02914D_{{\rm{eq}}}^2 + 0.9263{D_{{\rm{eq}}}} + 0.07791)\\ {c_2} = - 0.01983D_{{\rm{eq}}}^2 + 0.4698{D_{{\rm{eq}}}} + 0.09538\\ {c_3} = - 0.06123D_{{\rm{eq}}}^3 + 1.3380D_{{\rm{eq}}}^2 - \\ \quad \quad 10.41{D_{{\rm{eq}}}} + 28.34\\ {c_4} = - 0.01352D_{{\rm{eq}}}^3 + 0.2014D_{{\rm{eq}}}^2 - 0.8964{D_{{\rm{eq}}}} + \\ \quad \quad 1.226{\rm{ for }}{D_{{\rm{eq}}}} > 4{\rm{ mm}}\\ {c_4} = 0{\rm{ for }}1.5{\rm{ mm}} \le {D_{eq}} \le 4{\rm{ mm}} \end{array} \right.$

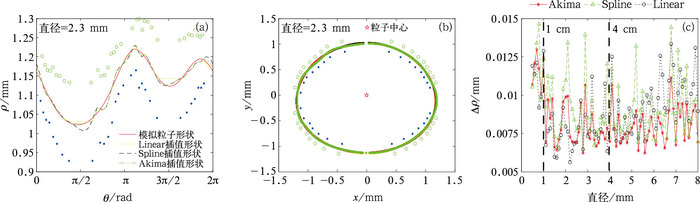
经坐标转换插值效果如图 6a所示，针对等效直径为2.3 mm的模拟雨滴，线性插值、Spline插值以及Akima插值均有较好的效果，但是Spline插值会在点较少的地方产生过度拟合偏离真实形状，而线性插值会在点较少的地方无弯曲度偏离真实形状。通过对以0.2 mm为间隔，0.4~8 mm的模拟雨滴进行讨论，其拟合的平方根误差如图 6c所示，当粒子等效直径<1 mm时，三种插值函数效果相同，但在1 mm<粒子等效直径<4 mm时，Spline插值效果明显变坏，在4 mm以上线性插值效果变差。因此采用Akima插值作为角点连续化方法将收到更好的效果。

4 实测雨滴形状特征 4.1 雨滴平均形状特征

由于实际大气中的雨滴受外部湍流、内部环流等因素影响，在下落的过程中处于摆动状态，致使雨滴产生形变和倾斜，与理论形状存在差异。但随着同一直径范围内雨滴数的增加，其对应的平均形状将趋于稳定，那需要多少个雨滴的平均形状才趋于稳定？现以0.2 mm为间隔，利用基于Akima插值的数字雨滴图像矢量化方法对不同直径范围内的实测雨滴进行处理，求取不同个数雨滴的平均形状与理论模型的差别，定义平均绝对偏差<ε>，表示在极坐标系下，实测雨滴的平均形状与理论模型形状间绝对偏差的平均值，其表达式如下：

$ < \varepsilon > = \left| {\sum\limits_{i = 1}^n {} \frac{{{\rho _{{\rm{raindrop}},{\rm{ }}i}}}}{n} - {\rho _{{\rm{model}}}} \times } \right|\frac{1}{n}$

(5)

式中，ρ_{raindrop, i}表示第i个雨滴对应某方位角上的内径，ρ_model表示雨滴理论模型与实测相同方位角上的内径。得到了不同直径范围内雨滴个数与其平均绝对偏差的关系(图 7)，当雨滴数<10时，其平均形状与雨滴模型差异较大；当10<雨滴数<100时，D<2.0 mm的雨滴其绝对平均偏差变化较为平缓，D>2.0 mm的雨滴变化幅度较大；当雨滴数>100时，不同直径范围内的雨滴平均偏差已基本趋于稳定，变化幅度在0.005 mm以内，且其稳定平均绝对偏差随着雨滴直径的增大而增大。因此，雨滴数在100个以上时，其平均的统计形状是基本稳定的，具有可分析的价值。

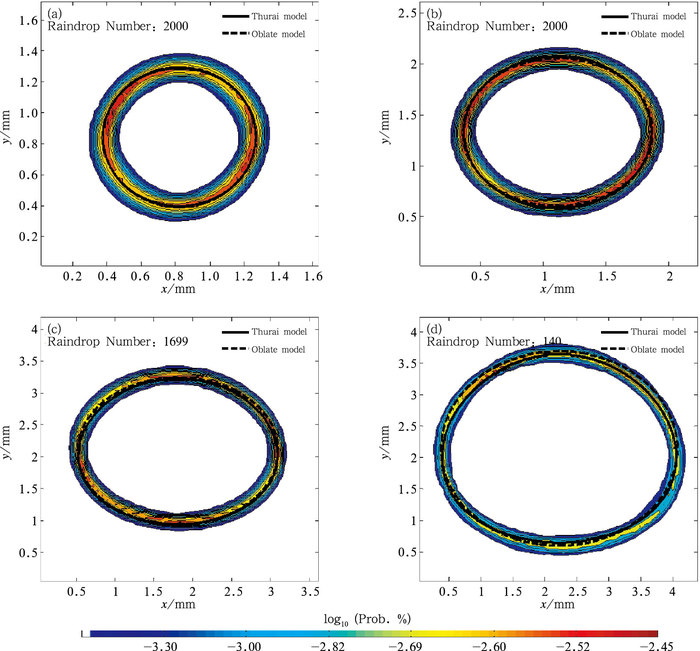
现仍然以0.2 mm为间隔，统计分析不同直径范围内的雨滴平均形状，由于雨滴数众多，无法利用散点图直接展示，因此利用统计等值图形式展现；即将原来的散点图，以一定的坐标间隔进行分块，统计每一小块上的雨滴形状点个数，将每个小块上的形状点个数与形状点个数总和相比，即得到坐标平面上雨滴形状出现概率的分布图(图 8)。图 8a~8d分别展示了0.8~1.0、1.4~1.6、2.4~2.6和3.4~3.6 mm等效直径范围内雨滴的概率统计形状，其中“Thurai model”代表该范围内平均等效直径利用式(4) 得到，“Oblate model”表示利用椭圆模型以该范围内雨滴平均长轴a和平均短轴b为长短轴所得。0.8~1.0 mm的雨滴其统计平均形状呈圆形，不同位置出现概率均匀分布于经验形状两侧；1.4~1.6 mm的统计平均形状呈椭圆形，其顶部相对于经验形状偏小，具有更扁的形状；2.4~2.6 mm的雨滴形状与1.4~1.6 mm的形状相似，但其顶部与椭球模型接近，底部相对经验分布偏小，具有更扁的形状；3.4~3.6 mm的雨滴形状与前三者具有明显的差异，其形状顶部凸起，底部展现明显的扁平状，与Thurai模型更为接近。通过对不同直径范围雨滴进行分析，总的来说雨滴形状随着等效直径的增加逐渐由圆形向椭圆形过渡(图 8a，8b)，再由椭圆形向顶部凸起，底部扁平过渡(图 8c，8d)；D<1 mm的雨滴以圆形为主，在1.0~3.0 mm的雨滴以椭圆形为主，D>3.0 mm的雨滴开始呈现较为显著的顶部凸起，底部偏平的形状，这一结论与Thurai and Bringi (2005)利用模拟降水试验所得结论一致。

4.2 轴比分布特征

轴比表示降水粒子的长轴与短轴之比，其分布特征反映了整次降水过程雨滴平均形状随等效直径的变化特征。该分布特征主要通过风洞实验、雨滴模型、双极化雷达观测以及雨滴谱仪实测获得，如Beard and Chuang (1987)利用BC雨滴模型得到服从四次多项式分布的轴比分布特征(1≤D_eq≤7 mm)、Goddard et al (1994)利用JWD雨滴谱仪与双极化雷达对比观测资料得到雨滴轴比分布服从三次多项式分布特征(1≤D_eq≤5 mm)、Brandes et al (2002)联合多人雷达观测轴比结论得到四次多项式分布特征的轴比分布(1≤D_eq≤7 mm)、Thurai et al (2007)利用2DVD雨滴谱对80 m人工降水进行测量同样得到了四次多项式分布特征的轴比分布(1.5≤D_eq≤8 mm)。现对所有实测雨滴进行处理，以0.2 mm为间隔得到的不同直径范围的轴比均值与标准差(表 2)，轴比分布特征以及与经验分布的差异如图 9所示，其中Δ表示实测轴比均值与经验轴比的差值。

从图 9a中可以看出，实测轴比均值整体随着等效直径的增加而逐渐减小，单个直径范围内的雨滴轴比呈高斯分布；标准差整体随直径的增加而逐渐减小，但在2.8~3.8 mm出现次峰值，主要原因是大粒子受湍流、低空风切变和碰并等因素的影响，不同方向的振动频率增加而造成。从图 9b中可以看出，整体来说，雨滴的平均轴比分布与经验分布较为一致，差异在±0.04范围内；当直径处于1.4~2.8 mm时，雨滴平均轴比分布与经验分布的差异在±0.01以内，较BC模型和TB模型的值偏大，较Brandes模型的值偏小；当直径处于2.8~4.0 mm时，雨滴平均轴比较所有经验分布值均偏大，整体与Brandes模型更为接近，在3.4~3.8 mm出现峰值，表明该范围内的雨滴形状相对于经验模型具有更圆的形状特征，主要因为Brandes模型综合更多实测轴比观测结果所得到的经验关系，更能反映大气中真实雨滴的轴比分布。

针对实测的轴比分布，由于当粒子直径<0.8 mm时，受图像噪声影响与真实雨滴形状存在较大差异，所以仅针对粒子直径>0.8 mm的雨滴采用四次多项式拟合，得到了式(6) 所示拟合结果，其RMSE为0.0063，相关系数为0.9981。

$\begin{array}{l} \frac{b}{a} = 1.2508 - 0.3585{D_{{\rm{eq}}}} + 0.1598D_{{\rm{eq}}}^2 - \\ \quad \quad 0.0359D_{{\rm{eq}}}^3 + 0.0028D_{{\rm{eq}}}^4 \end{array}$

(6)

为了将轴比分布特征应用于双偏振雷达定量估测降水(Marzuki et al，2013)，其一次拟合函数所得到的系数可直接应用于差传播相移率(K_DP)的计算，具体一次函数拟合结果如式(7) 所示，其RMSE为0.0067，相关系数为0.9962，适用范围为0.8~4.0 mm。

$\frac{b}{a} = 1.0738 - 0.0683{D_{{\rm{eq}}}}$

(7)

5 结论

本文利用降水微物理特征测量(PMCS)在南京地区的雨滴观测资料。分析了图像异常值的形成原因和处理方法，以此为基础重点研究了在极坐标下基于Akima插值的数字雨滴图像矢量化方法。通过统计234093个有效雨滴图像，得到了雨滴平均形状特征和轴比分布特征，有助于准确掌握雨滴微物理结构特征，从而为天气雷达定量估测降水、雨致微波衰减特征等方面研究奠定基础。

(1) 总体而言，雨滴形状随着等效直径的增加逐渐由圆形向椭圆形过渡，再由椭圆形向顶部凸起，底部扁平过渡。直径<1.0 mm的雨滴以圆形为主，直径在1.0~3.0 mm的雨滴以椭圆形为主，直径>3.0 mm的雨滴开始呈现较为显著的顶部凸起，底部扁平的形状。

(2) 雨滴的平均轴比随等效直径的增加而逐渐减小。其分布与经验分布基本一致，差异在±0.04范围内，当直径处于2.8~4.0 mm时，雨滴平均轴比较所有经验分布值均偏大，整体与Brandes模型更为接近，直径在3.4~3.8 mm出现峰值，表明该范围内的雨滴形状相对于经验模型具有更圆的形状特征。

(3) 基于Akima插值的数字雨滴图像矢量化方法会受雨滴二值图像测量精度的影响降低雨滴形成的提取精度，因此下一步将重点考虑雨滴图像复杂边缘变化情况，研究动态估计雨滴形状方法，降低雨滴矢量形状对二值图像精度的依赖性，进一步提高描述雨滴形状的准确性。

致谢：感谢南京信息工程大学大气物理学院黄兴友教授在外场试验及太原航空仪表有限公司南京分公司在搭建和调试仪器中所给予的帮助与支持。