引言

在数值模式中，微物理参数化方案直接描述成云致雨的过程，而云粒子分布谱及其变化是云降水过程的关键。综合计算效率和效果两方面的需求，云物理过程的描述多采用参数化的方法。大量研究表明, Γ分布更接近于自然降水粒子谱分布, 其被广泛地应用于云物理研究中(陈宝君等，1998；陈晓敏等，2011；高茜等，2011；罗俊颉等，2012；石荣光和刘奇俊，2015)。假设粒子服从Γ分布函数，即：N (D)=N₀D^μe^-λD。其中N是粒子数浓度(单位：m^-3)，三个待定谱参数截距N₀(单位：mm^-1-μ·m^-3)、斜率λ(单位：m^-1)、谱形参数μ决定了粒子谱的发展演变(许焕斌和段英，1999)。

雨滴是云的动力过程、微物理过程的最终结果, 也是实际业务预报中最为关心的物理量场之一。雨滴谱谱形函数(μ_r)对雨滴谱的演变起着至关重要的作用。云物质中大粒子由于较大的下落末速度往往更快地沉降下落，从而出现粒子平均直径随高度增加而降低的现象。μ_r越大(小)粒子的沉降速率越小(大)。降水的产生是雨滴下落的直接结果，因此方案中对雨滴谱谱形参数描述得过低(过高)引起沉降过快(过慢)都会对降水产生直接影响。雨滴谱的分布与雨滴相关的碰并、蒸发等微物理源汇项也息息相关(Milbrandt and Yau, 2005a; 赵震和雷恒池, 2008)。

实际观测表明，随着降水类型、降水地区和季节的不同，雨滴谱谱形参数(μ_r)的均值以及变化区间存在显著差异(Ulbrich，1983；Uijlenhoet et al, 2003；Meyers et al, 1997；房彬等，2016)。然而目前参数化方案中往往将μ_r设置为固定的常数，方案所描述的雨滴谱演变同实际情况还存在明显差距。那么如何在方案中反映出真实的雨滴谱谱形参数的时空变化信息成为急需解决的重要问题。事实上Γ分布函数的三个参数N₀，λ，μ相互之间并不独立。Chu and Su (2008)基于粒子谱分布的相关理论推导证明斜率和谱形参数两者之间的二项式关系具有明确的物理意义，并证明其关系的关键因子是雨滴平均直径所在的数浓度同雨滴总的数浓度的比值。μ-λ二项式关系也在观测研究中得到广泛证实。尽管拟合经验公式系数因地区、降水类型等因素存在一定的差异，但二项式函数关系都能够稳定存在(Nakagawa et al, 1996; Vivekanandan et al, 2004; Zhang et al, 2001; 2003; Brandes et al, 2004；Chen et al, 2011; 陈磊，2013；陈聪，2011; 熊飞麟和周毓荃，2016)。

基于以上观测事实以及谱参数之间的诊断关系，学者们针对谱形参数进行了诸多的数值试验研究。Milbrandt and Yau (2005a;2006a)通过基于μ-D(平均直径)诊断关系的函数假设改善了沉降过程和雹暴的模拟。Seifert (2005;2008) 将μ-λ(D)关系式分别耦合至云模式及双参数暖云方案后对云系微观特征和降水率的模拟都有改善效果。Adam et al (2014)适当增加雨滴谱谱形参数的取值更好地再现层状云雨滴谱的微观特征。

总体而言在方案中更加准确地反映μ_r的信息能够对模拟效果产生正的贡献。江淮流域的梅雨期间是短时强降水、雷雨大风等灾害性天气的高发期, 而目前在这方面针对梅雨降水的微物理参数化方案的改进研究还较少。实际雨滴谱观测表明，梅雨期间雨滴谱的谱形参数并非常数且与雨滴谱斜率之间存在较好的二项式函数关系特征。本文尝试基于μ-λ二项式关系式对Milbrandt 2-mon双参数方案中雨滴谱的谱型参数的描述精度进行改善。通过敏感性试验考察完善参数化方案中雨滴谱谱形参数信息对江淮梅雨降水模拟效果的影响，并对μ_r影响降水的可能机制以及不同强度降水下物理量场的响应特征进行了初步的分析。

1 模拟方案 1.1 模式设置及方案简介

利用非静力中尺度数值模式WRF 3.5.1, 对四次典型梅雨锋云系降水过程进行数值模拟。使用NCEP间隔6 h的FNL 1°× 1°再分析资料作为模式初始条件和边界条件。试验采用两重嵌套网格, 空间分辨率分别为9、3 km，垂直分层为不均匀的51层，表 1给出了具体的方案设计。文中所采用的微物理参数化方案是Milbrandt-Yau双参数化方案(MY)。该方案对所有的水凝物均采用双参数方法预报，共包含云滴、雨滴、冰晶、雪、霰和冰雹的比含水量和比浓度，以及水汽混合比共13个变量(Milbrandt and Yau, 2005a; 2005b; 2006a; 2006b)。方案考虑了较为全面的各类云物理过程，包括碰并和繁生、冻结和融化、凝华(升华)和凝结(蒸发)等云物理过程。为增强该方案在不同条件下的适应能力，方案提供了许多微物理过程以及经验公式的选择开关，用户可以根据需要进行设置。

1.2 试验设计

本文选取近年来四次典型的江淮梅雨个例(表 2)，尝试对Milbrandt 2-mon方案中的雨滴谱谱形参数进行改进。控制试验中相关参数的设置均为默认值。在MY方案中，雨滴谱谱形参数默认作为固定值0。μ和λ之间的二项式拟合公式具有显著的地域差异性。所以本文中所采用的斜率-谱形参数关系的经验公式源自陈磊(2011)针对江淮梅雨的已有研究工作。该工作对于数据观测以及资料处理方法等方面的误差都进行了相应的控制，拟合的二项式函数关系具有较高的可信度(图 1)。尹金方(2013)基于观测数据总结得出相关云物质在东亚地区的分布特征。本文的敏感性试验基于其研究，设置雨滴谱谱形参数0~6区间变化，比较符合东亚地区的特点。

本文尝试在方案中引入该经验拟合公式，使方案对雨滴谱的描述更加准确和符合本地化的特征。图 1为4个经验公式(A~D)的分布图。斜率随谱形参数呈现单调递增的趋势。随着雨滴谱谱形参数的增加，雨滴谱的斜率呈现下降趋势，粒子谱中大粒子也逐渐增多。太大的观测斜率可能来自于观测误差而非真实的物理过程。

方案中假设雨滴的粒径分布服从Γ分布n_x(D_x)=N_0xD^μ_xe^-λ_xD_x其中，n_x是粒子数浓度(单位：m^-3)，待定谱参数N_0x，λ_x，μ_x分别代表截距(单位：mm^-1-μ·m^-3)、斜率(单位：m^-1)和谱形参数。方案中假设雨滴为球形，可得

${\lambda _r} = {\left[ {\frac{{\pi {\rho _r}{N_r}\Gamma (4 + {\mu _r})}}{{6\rho {q_r}\Gamma (1 + {\mu _r})}}} \right]^{\frac{1}{3}}}$

(1)

${N_{0r}} = \frac{{{N_r}{\lambda _r}^{1 + {\mu _r}}}}{{\Gamma (1 + {\mu _r})}}$

(2)

谱形参数确定的前提下，斜率和截距可由混合比和数浓度q_r和N_r诊断获得。方案默认雨滴谱谱形参数为0，此时粒子的分布变成M-P分布，即n_x(D_x)=N_0xe^-λ_xD_x。而当μ-λ拟合关系式满足二项式关系式，即：

${\lambda _r} = A\mu _r^2 + B{\mu _r} + C$

(3)

式(3) 带入式(1)，可得：

$\begin{array}{l} 6\rho {q_r}{[A{\mu _r}^2 + B{\mu _r} + C]^3} = \\ \quad \quad \quad \pi {\rho _r}{N_r}(3 + {\mu _r})(2 + {\mu _r})(1 + {\mu _r}) \end{array}$

(4)

在已知混合比和数浓度的条件下通过牛顿迭代法对该谱形参数的一元六次多项式进行数值解的求解。由于所设置的雨滴谱谱形参数大于0，易知在本文所设置的变化区间内雨滴谱谱形参数最多只有一个实数解；雨滴的斜率、截距、平均直径、加权速度等变量也可以在此基础上诊断得出。雨滴谱谱形参数在方案中与许多微物理过程密切相关，为了更加准确地再现雨滴谱谱形参数随时空变化对雨滴谱演变过程的影响，对所涉及上述相关变量的所有微物理过程的计算均需要在文献Milbrandt and Yau (2005b)的基础上进行改写。由于该方案预留了升级为三参数方案的接口，雨滴谱谱形参数已经作为单独的变量保留，这也方便了相关的改写工作。相关微物理过程包括：雨滴凝结(蒸发)、雨滴碰并云滴、雨滴的聚并和破碎、冰晶、雪、霰、雹同雨滴的碰并凇附过程以及雨滴的沉降过程、雨滴冻结等。本文3.1节中对相关参数化方法进行了简略的介绍，具体计算公式请参考Milbrandt and Yau (2005b)。

2 模拟结果分析 2.1 检验方法

模式系统预报的降水以检验其落点预报为主, 检验区域为江苏区域。选2011—2013年四次梅雨个例的江苏地区地面区域加密自动站的降水资料作为降水检验的指标站, 将预报的降水格点(细网格)场资料采用双线形插值方法插到站点上得到站点的降水预报值。文中降水模拟效果的检验主要分为24 h累积降水和1 h降水(以下以R代表降水量)。其中为了更加客观和综合地评估试验的结果，共采用TS、ETS、击中率(POD)、虚警率(FAR)和预报偏差(BR)5个降水检验统计量。

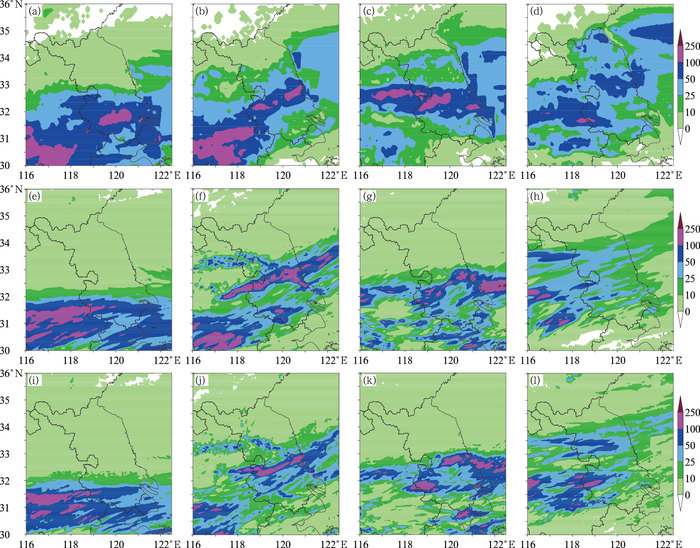
2.2 24 h累积降水

图 2给出观测和模拟的24 h累积降水分布(对各经验公式的代表性结果进行展示)，从中可以较为宏观地了解个例模拟降水的总体特征。各控制试验中，模拟雨带的分布同观测基本一致，诊断谱形参数对降水的系统性偏差也具有一定的改善能力。其中个例3强降水区集中在沿江及两侧，控制试验的雨带总体略有偏南，暴雨区偏窄。改进试验对西侧的强降水区有显著增强改善作用(公式A最为显著)。个例4控制试验的降水强度总体偏弱，暴雨以上等级的降水区几乎未模拟出。耦合λ-μ二项式关系后各经验公式使得降水强度显著增强，江淮之间的暴雨区也能够基本呈现(图 2l)。个例2暴雨以上的降水区强度略强。改进试验对大雨区南北跨度偏窄的情况均有不同程度地改善，南部的虚假强降水区也显著削弱(图 2j)。而个例1主雨带分布在沿江苏南地区，诊断谱形参数使强降水区总体削弱，仅经验公式D中南京附近的大暴雨中心仍然维持。

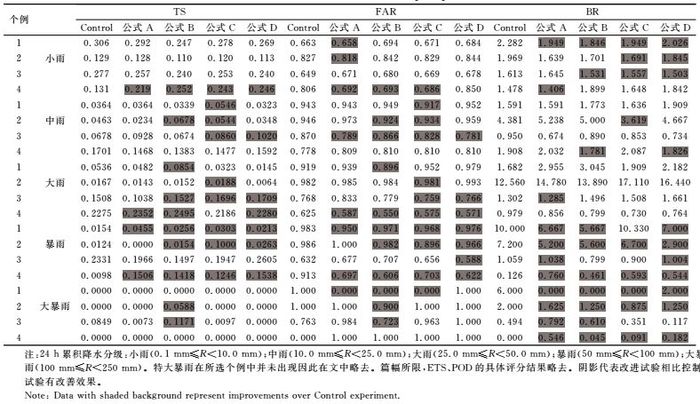
为了更加客观地了解诊断谱形参数方法对24 h累积降水的改善能力(表 2)，计算了各试验24 h累积降水的客观评分(表 3，篇幅所限，ETS、POD的具体评分结果略去)。改进试验对不同等级的降水的影响呈现显著的差异。其中对小雨、大雨的预报无明显促进作用甚至呈现恶化趋势：小雨时各拟合经验公式对降水的影响较为一致，除个例4，评分均呈现(POD、ETS、TS)下降趋势；小雨的降水范围同观测的差距虽然已显著缩小但空报现象仍然突出。而大雨的降水改进效果也并不显著(TS、ETS、POD)，降水的范围偏广的现象总体也呈现恶化趋势。

利用斜率诊断雨滴谱谱形参数的改善方法对中雨、暴雨和大暴雨的模拟准确率有较明显的改善效果：中雨(TS、ETS)和暴雨(TS、ETS、POD)时降水准确率和空报现象分别表现出显著的增加和削弱趋势；暴雨的降水范围也愈加接近观测(个例1和2中暴雨范围过广的现象得到显著削弱)，各拟合公式对大暴雨的降水范围的把握更加准确。这一定程度上表明，在已有的大尺度的降水环流背景下，完善谱形参数的信息对降水落区分布的局地特征能够发挥一定的修正作用。其中各个经验公式也表现出不同的能力：中雨时C经验公式对中雨的评分改进更具优势(TS、ETS、POD)，暴雨时D经验公式改善效果最优(TS、ETS)，而大暴雨中B经验公式的改善效果最优(TS、ETS、POD、FAR)。

2.3 1 h降水

相比24 h累积降水，1 h降水更能够反映降水在时间上的集中程度，对防灾减灾也尤为重要。在控制试验中，随着雨强的增加，评分总体降低(表 4)。暴雨和短时强降水由于降水范围集中以及持续时间较短，模式对它们逐小时演变规律的捕捉较为困难。与24 h累积降水类似，改进试验在不同等级降水中的表现并不一致。改进试验对小到大雨等级的降水无明显改善效果。其中各个经验公式的应用使个例3、4的小雨TS和ETS全部下降。大雨的预报准确率(TS、ETS、POD)也没有显著改善，但空报现象有所削弱，降水范围也更加接近观测。中雨时总体表现较为平稳。改善和恶化的样本数约各占一半(TS、ETS、POD、FAR)。

而改进试验中暴雨(TS、ETS、POD)、短时强降水(TS、ETS、POD)的预报准确率显著提升, 这与Shipway and Hill (2012)的研究结果一致。暴雨时经验公式B的准确率改善效果最佳，其次经验公式A；经验公式B和公式D对空报现象也有较好的抑制效果(FAR)。短时强降水时，经验公式C表现最佳，其次经验公式B。空报现象和预报偏差总体比较平稳。暴雨和短时强降水时也存在改进试验的降水范围总体偏窄，甚至出现同观测差距加大的现象。

3 雨滴谱谱形参数对降水过程的影响分析 3.1 云物理特征

耦合μ-λ二项式关系对梅雨降水产生了显著的影响，且具体特征因降水强度而异。总体而言，较强降水对雨滴谱谱形参数的完善有显著的改善倾向。文中首先尝试从云系微观特征的角度初步分析谱形参数对降水的影响机制以及不同强度降水时物理量的响应特征差异。文中选取了1 h降水中的小雨和暴雨两个量级的降水(进行区域和时间平均处理)分别作为弱降水和强降水的代表进行分析。

降水是云物理过程的最终产物，而改进试验中云物理过程相比于控制试验所发生的变化都起源于雨滴谱谱形参数的变化。耦合经验公式后，雨滴谱谱形参数变化显著，总体大于控制试验所设置的常数0。μ_r自地面起随高度增加呈现弱的波动，到达0℃层附近时迅速增加并在冷云中保持较大的数值。其中小雨时μ_r自地面附近由0.5随高度总体缓慢增加至2.25(600 hPa), 而暴雨时暖云中μ_r主要集中于0~0.5(图 3a、图 3e)。随着雨强的增强，雨滴谱分布在较大滴端逐渐上抬，斜率逐渐变小，μ_r也逐渐减小，以上模拟结果同观测事实较为一致(陈磊，2011)。

谱形参数对粒子谱的发展演变的直接影响主要涉及两个方面：

其一是对沉降过程的影响。

雨滴下落末速度为V_r=a_rD_r^b_r, a_r=149.100, b_r=0.5000(Tripoli and Cotton, 1980) (默认国际单位制)。由于重力作用大雨滴下落得更快，粒子的平均直径将随高度降低而增加。沉降过程使得垂直方向的各个高度的粒子谱形重新调整。雨滴的质量加权平均下落速度V_Qr和数浓度加权平均下落速度V_Nr的比值，称为沉降速率，即

$\begin{array}{l} \quad \frac{{{V_Q}_r}}{{{V_{Nr}}}} = \frac{{\Gamma (4 + {b_r} + {\mu _r})\Gamma (1 + {\mu _r})}}{{\Gamma (4 + {\mu _r})\Gamma (1 + {b_r} + {\mu _r})}}\\ = \frac{{(3 + {b_r} + {\mu _r})(2 + {b_r} + {\mu _r})(1 + {b_r} + {\mu _r})}}{{(3 + {\mu _r})(2 + {\mu _r})(1 + {\mu _r})}} \end{array}$

(5)

该参数可以用来描述粒子谱形的调整速度。随着雨滴谱形参数的增加沉降速率减小并趋近于1；当雨滴谱形参数由0增加至1(3) 时，沉降速率降低26.7%(41.6%)。沉降速率越大(小)，较大的平均半径越有可能出现在较低(高)的高度上。

图 3d和图 3h中模拟的雨滴平均直径总体随高度降低而增加的特征同实际观测较为一致(Christine, 2015)。耦合经验公式后，无论是小雨还是暴雨，对流层中低层(液态云主体)的雨滴平均半径均表现出显著增强的特征。这是雨滴谱形参数增加所带来的直接影响。相比于控制试验中雨滴谱谱形参数设置为0的情况，敏感性试验中μ_r总体增大，谱分布变窄，斜率增加。同时粒子谱中的大雨滴数量比例降低，沉降速率减小，雨滴在液态云的中上层往往能够停留更多的时间，经过充分的增长产生更大的平均直径。强降水时雨滴含水量和数浓度更大，耦合经验公式带来的沉降速率的减弱效应在此时更为显著。而μ_r增加后，雨滴粒子谱分布的垂直调整变弱，改进试验中暴雨条件下高低层的雨滴平均半径差距也出现了显著缩小的现象。

其二是对雨滴的微物理源汇项的影响。

雨滴的微物理源汇项分别对应着不同的阶距。因此理论上谱形参数对微物理源汇项的影响可转化为分析其对不同阶数矩的作用(后文中的讨论均默认在雨滴谱形参数≥0的范围内进行)。

粒子x的p阶距：

${M_x}\left( p \right) = \smallint _0^\infty {D^p}{n_x}\left( D \right){\rm{d}}D = \frac{{{N_{0x}}\Gamma (1 + {\mu _x} + p)}}{{}}\lambda _x^{1 + {\mu _x} + p}$

(6)

定义比值

$\begin{array}{l} R{\rm{ }}(p,{\rm{ }}{\mu _2},{\rm{ }}{\mu _1}) = \frac{{M{\rm{ }}(p,{\rm{ }}{\mu _2})}}{{M{\rm{ }}(p,{\rm{ }}{\mu _1})}}{\rm{ }}\\ \quad \quad \quad \quad \quad \quad = \frac{{\Gamma (1 + {\mu _1})\Gamma (1 + {\mu _2} + p)}}{{\Gamma (1 + {\mu _2})\Gamma (1 + {\mu _1} + p)}} \times \\ \quad \quad \quad \quad \quad \quad {\left[ {\frac{{\Gamma (1 + {\mu _2})\Gamma (4 + {\mu _1})}}{{\Gamma (4 + {\mu _2})\Gamma (1 + {\mu _1})}}} \right]^{\left( {p/3} \right)}} \end{array}$

(7)

式中, M (p, μ₂)为用μ₂值计算的p阶距, M (p, μ₁)为用μ₁值计算的p阶距。

控制试验中雨滴谱谱形参数为0，则上式简化为：

$R{\rm{ }}(p,{\mu _2},{\rm{ }}0) = \frac{{\Gamma (1 + {\mu _2} + p)}}{{\Gamma (1 + {\mu _2})\Gamma \left( {1 + p} \right)}}{\left[ {\frac{{6\Gamma (1 + {\mu _2})}}{{\Gamma (4 + {\mu _2})}}} \right]^{\left( {p/3} \right)}}$

(8)

图 4a是比值R (p, μ₂, 0) 随雨滴谱谱形参数和阶距值变化的演变图，可以发现，当p=0或者3时，比值R恒为1，即0阶距或3阶距M (p)不受μ_r取值的影响；当p＜3时，μ_r增加时，R值增加且大于1，M (p)增大，可知相关微物理过程的转化率在理论上应得到增强；而p>3时, μ_r增加时，R值降低且小于1，M (p, μ)减小，相关微物理过程的转化率在理论上应得到削弱。

雨水含水量(RWC)和雨滴数浓度(N_r)分别对应M(3) 和M(0)，与理论推测不一致的是，两者并没有保持不变而是对μ_r的取值产生了显著的响应特征(图 3b和3c及图 3f和3g)。相比控制试验，小雨和暴雨在改进试验中的RWC和N_r均表现出一致的减弱趋势。小雨时RWC和N_r在对流层附近达到最大值，并随高度降低总体下降，这可能与蒸发作用密切相关。暴雨时，水汽供应充足，RWC和N_r均显著高于小雨的情况与观测事实较为一致(陈磊, 2011)。暴雨时对流层中低层(约600 hPa以下)N_r在改进试验中呈现出总体随高度下降而增加的特征。这可能与此时较好的水汽饱和条件下蒸发过程较弱，大雨滴更易发生破碎有关。

降水强度与地面附近的雨滴的下落速度和雨水含量的乘积有关。在近地面弱的环境垂直运动条件下，改进试验的雨滴中大粒子的增多，雨滴质量加权末速度增大(图略)，而雨滴含水量却显著减弱。这是降水发生变化的直接原因，而两者呈现出的相反的响应趋势也直接导致了改进试验中不同等级降水率变化的差异性。

雨水含水量的显著变化与参数化方案的雨滴源汇项密切相关。与雨滴谱形参数直接相关的云物理过程包括：(1) 雨滴碰并云滴：μ_r的取值对雨滴碰并云滴后雨滴混合比的增加及消耗的云滴并无直接影响。而当雨滴平均半径D_r＜100 μm时，碰并过程使得云滴减少的数量(M(6))随着μ_r的增加而迅速减少(Cohard and Pinty, 2000)。(2) 雨滴的蒸发(凝结)：雨滴蒸发消耗的混合比对应M(1)、M(1.5+0.5b_r)[即M(1.75) ]并随着μ_r增加而增加。雨滴的凝结并未考虑(Ziegler, 1985)。(3) 雨滴聚并和破碎：仅仅当雨滴平均半径D_r＜100μm时，小雨滴的自我聚并过程[M(6) ×M(0) ]有所削弱；就雨滴的破碎过程而言，D_r＜600μm或>2mm时, 其转化率受μ_r具体取值影响[参见Cohard and Pinty, 2000中公式(24)、(25)、(26) ]。(4) 雨滴同冰相粒子的凇附过程：当质量加权平均的雨滴和冰相粒子的下落末速度差较大时，随着μ_r的增加, 凇附过程所消耗的雨滴混合比减少，而所消耗的N_r同μ_r的具体取值以及与雨滴碰并粒子的性质相关。当两者速度较为接近时，所涉及的混合比和数浓度的变化同μ_r的具体取值以及冰相粒子的性质相关(Murakami, 1990)。(5) 其余过程：融化过程仅仅与冰相粒子自身的性质有关不受μ_r具体取值的影响。理论上雨强[M(3+b_r)]随着μ_r的增加，降水应呈现减弱趋势。另外由于本文中雹物质很少，因而略去相关过程的讨论。

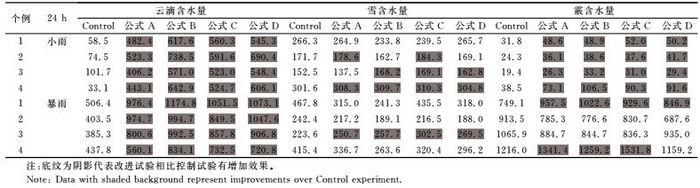
雨水的形成往往与雨滴碰并云滴及冰相粒子的融化两类过程密切相关。通过上述理论分析可以初步理解雨滴谱谱形参数取值对相关的每一类云物理过程的直接影响，以及推测雨滴谱形参数对雨水形成过程的可能的影响趋势。理论分析中μ_r对雨滴碰并云滴时所消耗的云滴混合比没有影响，而模拟结果表明，小雨和暴雨情况下，云滴含水量均出现了显著的增强趋势(表 5)，尤其是0℃层附近以下的高度。实际上三维数值模式的实际模拟积分过程中，各种微物理过程之间以及与模式动力和温湿环境之间存在复杂的相互作用和非线性反馈特征，使得很难将雨滴谱谱形参数对每一类微物理过程的具体影响作用单独剥离出来，理论分析中单一的对应关系也并不适用。而改进试验中雨滴含水量一致减弱的情况一方面可能与云滴向雨滴自动转化以及雨滴碰并云滴的过程减弱有关，另一方面小雨滴的聚并作用减弱以及雨滴蒸发过程加强也可能产生影响。

文中个例的过冷水中主要以云水为主，因而雨滴谱形参数通过同冰相粒子的碰并凇附等过程对冰云的直接影响较为有限。而在μ_r所带来的复杂的间接非线性反馈作用(增加的云滴含水量加强了凇附过程等)下，改进试验中冰云的响应特征十分显著，0℃层附近的总的固态冰相粒子含水量也呈现复杂的变化特征，对雨水的形成产生重要影响(图略)。模拟的0℃层附近的冰云主要由雪和霰构成，冰晶云的主体位于400 hPa以上的高空，对雨水的形成主要是间接贡献。计算结果表明除小雨时改进试验中霰含量呈现总体的一致的增强趋势外，小雨和暴雨时的其余冰相物质的响应特征更加复杂，均因个例和拟合公式而异(表 5)，没有一致的变化趋势可循。暴雨时，云系发展更为深厚，冰相粒子含量更高，冰相粒子的响应特征更为强烈。

暖云中云物质的特征在强弱降水时虽然均呈现出一致的变化特征，但是两者同一物理量的量级、垂直分布存在显著差异，变化幅度也有明显区别。而在冰云中强降水的云物质的变化趋势的一致性更差一些。

3.2 水汽与动力条件

降水的发生是天气动力学过程和云物理过程相互作用的结果，天气动力学等“宏观”过程是“云”发展与演变的环境条件(孙继松，2014)。因而改进试验中云系出现的大范围的显著的响应特征与环境场的调整也密切相关。相对湿度体现了环境场水汽饱和程度，反映了温度和湿度双重因子的综合影响，是云系发展的必要条件。改进试验中，小雨时的对流层中低层(600~800 hPa)的水汽条件更加饱和，600 hPa以上的高度内则呈现出总体变干的趋势(图 5a)。如此不稳定结构得到增强的现象，可能是小雨时垂直上升运动获得加强的主要原因之一。小雨时改进试验的下沉运动表现出一致的增强趋势则可能与粒子的动力拖曳和雨水蒸发冷却效应的加强有关。

暴雨时云系发展更为旺盛，各种动量和热量的垂直输送也更加地剧烈。暴雨时的对流层中高层的变化更为显著(相对湿度和上升运动)，云物质和环境场的调整相比小雨时更为深厚。此时对流层中低层的下沉运动均表现出较一致的增强趋势，但湿度场以及上升运动在不同个例不同的经验公式条件下变化趋势并不一致。与前文中冰云物质的响应特征类似，暴雨的水汽和动力条件在不同的个例及经验公式中对谱形参数增加后的响应特征一致性相比于小雨情况较差。这可能与强降水条件下云微物理过程更加地剧烈，云物理过程以及环境条件之间的非线性反馈作用更加复杂有关。

受到云物理过程潜热释放和粒子拖曳等过程的影响，环境背景场中的温湿和动力条件产生了相应的反馈和调整，继而对决定云系的发展演变、降水的位置和强度方面也起到了关键的作用。因而环境场的调整和是改进试验的降水发生变化的间接原因。

参考所选个例的雨滴谱形参数的变化范围可知(图 3a和3e)，相同混合比和数浓度条件下，μ_r的中低值区内(0~2.5) 四个公式诊断获得的雨滴谱形参数从小到大依次为A、C、B、D，这一特征在敏感性试验的实际模拟结果中得到了一定的体现。小雨时0℃层以下的液态云主体中(图 3a)，各敏感性试验分别耦合A、C、B、D公式的试验结果同样存在μ_r依次增大的趋势，这与理论计算结果十分一致(图 1)，并且相应的模拟微观特征中雨滴的平均半径、雨滴数浓度也存在显著的线性特征。而暴雨时(图 3e)，不同拟合公式μ_r以及微观特征的模拟值的大小排序同经验公式的结果存在显著的差异。

4 结论与讨论

Milbrandt 2-mon (MY)双参数微物理方案采用Г谱分布函数时，对于粒子谱的谱形参数并未预报而是设定为常数0。本文利用WRF 3.5.1模式中的MY双参数方案耦合四种基于梅雨雨滴谱观测的μ_r的经验诊断公式，对2011—2013年四次典型的江淮梅雨降水过程进行数值模拟，重点探讨了引入诊断公式后对梅雨降水的影响以及降水变化的初步原因，并分析了不同强度降水时物理量场的响应特征。文中主要得出的结论如下：

(1) 利用斜率诊断雨滴谱谱形参数的处理方式对梅雨降水的系统性偏差有一定的改善能力，个例中虚假强降水区和降水总体偏弱的情况得到一定的抑制，对降水落区分布的局地性特征能够发挥一定的修正作用。较强降水对雨滴谱谱形参数的完善有显著的改善倾向：诊断公式对24 h的中雨、暴雨和大暴雨以及1 h的暴雨、短时强降水模拟准确率均有较明显的改善效果。

(2) 对流层中低层的雨滴谱谱形参数随降水强度增加而降低。雨水含水量的减小、雨滴质量加权末速度的增加是改进试验中降水变化的直接原因，其中雨滴平均半径增加是雨滴谱谱形参数总体增加的直接结果，而暖云中的云水向雨水质量的转移过程减弱是雨水含水量减少的主要原因之一。环境场的水汽和动力条件的改变是降水变化的重要间接原因，与雨水形成过程有关的云水含量的显著增幅以及冰相物质的复杂的响应特征都与此密切相关。

(3) 强弱降水的改善程度差异主要源于各自物理量场的响应特征的不同。暖云中，强弱降水时的云物质特征变化趋势一致但具体数值、分布和变化幅度差异显著。弱降水条件下，耦合不同经验公式及不同个例时，物理量场的响应特征表现出较为一致的变化趋势和一定的线性特征。而强降水条件下，云系发展更为旺盛，环境水汽和动力条件以及云物质的调整更为深厚和剧烈。此时云物理过程以及同环境条件之间反馈作用更加复杂，冰云和环境场的响应特征往往没有明显规律可循。

由于篇幅所限，文中就雨滴谱形参数对降水的影响机制仅做了初步的分析。同时鉴于经验公式的局地性限制以及方案改进方法不够完善，文中的改进试验结果还存在一些不足之处。这些都有待于在后续工作中进一步补充和完善。