引言

由于大气运动的混沌特征，数值预报初值误差会随着积分时间的延长呈指数式增长(Lorenz，1963)。为了定量地表征初值和模式误差给预报结果带来的不确定性，开发了集合预报系统(Ensemble Prediction System, EPS)，通过对初始条件(和/或数值模式)的随机扰动，进行蒙特卡罗试验，进而从概率的角度提高数值模式的预报性能(Molteni et al, 1996；李泽椿等，2014)。

集合成员的增加，意味着计算量的增加，为了保证集合预报的时效性，相对于确定性模式，EPS需要降低模式的分辨率。ECMWF EPS的分辨率一般是确定性模式的一半(Palmer et al, 1993; World Meteorological Organization WMO, 2012)，相对于EPS，确定性模式是一个较高分辨率的模式(High-resolution Deterministic forecast, HDet)。在模式性能和初值分析技术一定的前提下，提高数值模式的分辨率是增强模式预报性能的有效手段(Buizza, 2008)。EPS分辨率的降低，有可能导致模式预报性能的降低(Simmons et al, 1989)。

EPS由于考虑了初值(和/或模式)的不确定性，引入了更多的成员，从概率的角度提高了数值模式的性能，而HDet相当于只有一个成员但分辨率更高的“集合预报系统”。前者的优势在集合成员多，后者的优势在分辨率更高。Boucher等(2011)对比了经过后处理的集合预报和确定性模式对2003年发生在加拿大的一次洪水事件的预报效果，结果显示前者明显优于分辨率更高的后者。Richardson(2000)运用相对经济价值的方法，对ECMWF EPS进行了检验分析，指出EPS在中期时效都具有正的相对价值，并且和HDet的对比显示，EPS具有更高的相对经济价值。但Gall等(2013)针对台风桑迪的路径，对比了ECMWF确定性模式与ECMWF EPS和NOAA其他两个EPS，结果却显示EPS的平均值和HDet具有相近的技巧。因此，针对具体的预报问题或预报对象，有必要对两者进行对比检验，从而系统性地反映两者的优劣，为应用提供参考。

淮河流域是暴雨的多发地区(Dong et al, 2011)，常常导致洪涝灾害，对这一地区暴雨(日降水量≥50 mm的事件)的预报显得尤为重要。本文针对这一地区的暴雨，对比分析ECMWF HDet和EPS的预报效果。

EPS含有较多的成员，因此要用EPS对极端天气进行预报，首先需要对EPS进行后处理，将其转化为极端天气的概率信息，之后用这一信息对极端天气进行预报和决策(Legg et al, 2004; Buizza et al, 2005; Raftery et al, 2005; Ruiz et al, 2009; Schmeits et al, 2010)。较为常用的后处理方法有极端天气预报指数(Extreme Forecast Index, EFI)(Lalaurette, 2003; Zsótér, 2006; Persson, 2011; 董全等, 2012；刘琳等，2013；杜钧等，2014；夏凡等，2012；汪娇阳等，2014)和极端天气发生概率(Hamill et al, 1998; Raftery et al, 2005; Sloughter et al, 2007; 韩焱红等，2013；刘建国等，2013；胡邦辉等，2015；张宇彤等，2013；2015；赵琳娜等，2015)。EFI通过对预报概率和气候概率之差的积分，巧妙地剔除模式的系统误差，所以在极端天气的预报中得到了非常广泛的应用(Petroliagis et al, 2012)。由于EPS的直接概率输出总是存在“欠发散”的现象，因此也可采用订正效果较好的改进型的贝叶斯模型平均(MBMA)(Schmeits et al，2010)对集合预报结果进行订正。本文对比检验HDet和基于EPS的日降水EFI与MBMA订正后的降水概率对淮河流域暴雨的预报。

对于一个给定的模式系统或者客观预报系统而言，其对某一气象要素预报的命中率和空报率是一一对应的，要想增大命中率必须增大空报率，要想减小空报率必然要以命中率的减小为代价，这一一对应的关系表现为ROC(Relative Operating Characteristic)曲线，ROC检验对模式的系统性偏差不敏感(Jolliffe et al, 2003)，在集合预报的检验中得到了广泛的应用(Chang et al, 2015)。HDet降水量预报普遍存在系统性偏差，而ROC检验对这一偏差不敏感。因此本文运用ROC检验的方法，并将其扩展到TS检验，对比了不同空报率对应的TS评分，这一TS评分同样对HDet、EFI和降水概率预报的系统性偏差不敏感，使得检验结果具有更好的可靠性。在此基础上，综合考虑预报决策取决于事件经济价值大小的因素，利用相对经济价值(Richardson, 2000；Zhu et al, 2002)的方法进行了检验。通过设定不同标准，计算和对比了不同方法对淮河流域暴雨的预报阈值。

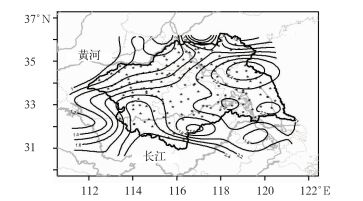
1 资料和方法 1.1 资料

本文运用中国气象局国家气象中心，淮河流域186个气象加密观测站点(图 1)，逐日20时至20时24 h累计降水量观测资料，TIGGE中心ECMWF集合预报系统和较高分辨率的确定性模式(Park et al, 2008)降水预报，以及国家气象中心预报员主观定量降水预报资料。

其中资料时间段为2007—2012年每年5—9月。数值模式资料空间分辨率为0.5°×0.5°，时间分辨率为24 h。集合预报系统最长时效为15 d，高分辨率模式最长时效为10 d。

由于实况观测和预报员主观预报都是针对站点，而HDet和EFI为格点预报，因此在对比研究中，采用双线性插值的方法，将格点值插值到站点上，之后进行对比。

1.2 极端预报指数和改进的贝叶斯模型平均

Lalaurette (2003)假设如果EPS中的某一事件相对于“模式气候”为极端事件，那么与之对应的实况天气相对于真实气候也为极端事件。基于这一假设，定义极端预报指数(EFI)。其原理和计算方法，以及为了增加其对极端降水事件的敏感性而进行的改进，请参考相关文献(董全等，2012；夏凡等，2012)。本文运用TIGGE归档中心2007—2011年共5年，48 h时效日降水预报量资料，每一个日历日前后15 d，共31 d滑动作为“模式气候”，由这155个样本构建的“模式气候”计算降水EFI指数(董全等，2012)，进行对比。

EFI主要对极端天气事件有较好的预报和指示意义，可用来对极端降水进行预警。Lalaurette(2003)和Dong等(2011)将过去30年的日降水序列中≥95%分位数的事件定义为极端降水。在淮河流域，这一阈值在20~30 mm·d^-1(图略)。为了预报和决策服务的需求，本文主要讨论暴雨及暴雨以上量级降水事件，即日降水量≥50mm的事件。

MBMA模型是基于贝叶斯全概率公式(Sloughter et al, 2007)，对于K个成员的EPS(本文为欧洲中心EPS，K=51)，预报降水量y的概率p(y|f₁, …, f_K)按照贝叶斯全概率公式为：

$\begin{array}{l} p(y|{f_1}, \ldots ,{f_K}) = \sum\limits_{k = 1}^K {{W_k}} \{ P(y = 0|{f_k}) \times \\ I\left[ {y = 0} \right] + P(y > 0|{f_k}){g_k}(y|{f_k})I\left[ {y > 0} \right]\} \end{array}$

(1)

式中，W_k为训练样本中，第k个成员预报正确的概率，可以视为常数，将降水分为无降水和有降水两部分，符号函数I[…]当方括号内的条件成立时为1，否则为0。等于0的概率用Schmeits等(2010)改进的逻辑回归模型：

$\begin{array}{l} {\rm{logit}}P(y = 0|{f_k}) = {\rm{logit}}P(y = 0|{f_1}, \ldots ,{f_K})\\ \quad \quad \quad \quad \quad = a_0^\prime + \frac{{a_1^\prime }}{K}\sum\limits_{k = 1}^K {f_k^{1/3}} \end{array}$

(2)

大于0的事件用皮尔逊三型分布来拟合，其pdf曲线为：

${g_k}(y|{f_k}) = \frac{1}{{\beta _k^{{\alpha _k}}\mathit{\Gamma }({\alpha _k})}}{y^{{\alpha _k} - 1}}\;{\rm{exp}}( - y/{\beta _k})$

(3)

其两个参数都是均值和方差的函数，即α_k=μ_k²/σ_k²，β_k=σ_k²/μ_k，均值μ_k和方差σ_k²可用线性拟合的方法估计，即μ_k=b_0，k+b_1，kf_k^1/3，σ_k²=c₀+c₁f_k。

未知参数a₀^′和a₁^′根据相应的逻辑回归法估计，b_{0, k}和b_{1, k}用线性回归的最小二乘法估计，W_k、c₀和c₁运用期望最大法(Expectation-Maximization Algorithm)来估计(Sloughter et al, 2007)。

1.3 经济价值

决策者根据未来天气预报概率的大小来决定是否采取措施，其中一个重要的考虑就是采取措施的经济价值。对气候发生概率为o的事件，假设某一预报系统预报后的总的花费为E_f，按照气候概率o预报时的总花费为E_clim，如果是完美的预报，总花费为E_perf，可以定义相对经济价值V为：

$V = \frac{{{E_{{\rm{clim}}}} - {E_f}}}{{{E_{{\rm{clim}}}} - {E_{{\rm{perf}}}}}}$

(4)

转换后可得(Richardson, 2000)：

$V = \frac{{{\rm{min}}\left( {r,o} \right) - fr\left( {1 - o} \right) + ho\left( {1 - r} \right) - o}}{{{\rm{min}}\left( {r,o} \right) - or}}$

(5)

式中，h为命中率，f为空报率，r为空报的损失C和预报正确后可以避免的损失L₁之比，称为花费损失比。

对于淮河流域的暴雨事件，运用1981—2010年共30年5—9月资料统计得，其北部和南部的气候概率分别为1.6%和2%左右(图 1)。整个淮河流域极端降水的空间一致性较好(Dong et al, 2011)，所以对淮河流域所有降水样本统一分析得，其暴雨事件的气候概率o为1.87%。

2 淮河流域暴雨主客观预报检验的对比分析 2.1 中央气象台主观预报检验

对淮河流域5—9月暴雨及暴雨以上量级降水的预报，中央气象台预报员不同预报时效的命中率在2007—2012年都呈现微弱的减小趋势，空报率逐年减小明显，尤其2011和2012年，不同时效空报率较为稳定地维持在0.017左右，TS评分从2007—2012年，存在一定的波动，线性趋势不明显。较明显的趋势是预报偏差在2007—2012年期间从2.0逐渐减小到1.4左右(图略)。可见中央气象台的预报服务更多地考虑到了预报偏差，在保持命中率和空报率基本稳定的前提下，保持预报偏差尽量接近1。

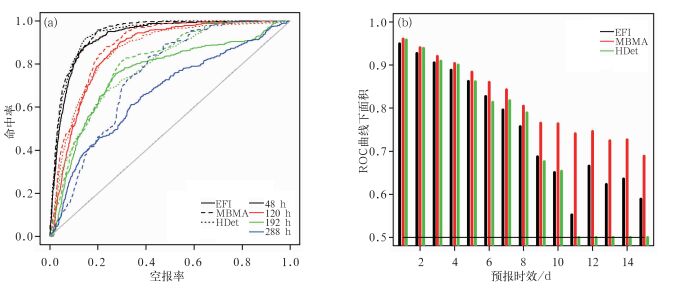
2.2 客观预报检验对比

从图 2的ROC检验可见，三种方法中，MBMA订正后的暴雨概率预报效果最好，其次是HDet，EFI的预报效果最差。MBMA在短期时效(1~4 d)内，相对于HDet的优势不明显，随着预报时效的延长，其优势进一步体现出来，尤其到了9 d以后，其效果明显优于另外两种方法。另外，对于9~10 d的预报，EFI的效果和HDet的接近。HDet没有10 d以上的预报，而EPS对10 d以上的预报，MBMA明显优于EFI(图 2b)。可见，EPS后处理的方法很重要，不同的方法订正效果会有显著的差异。

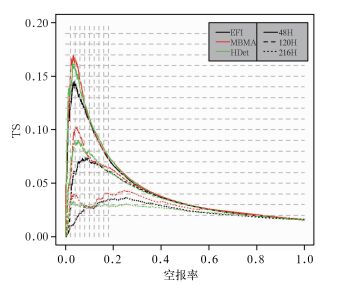
在预报业务中，检验预报的优劣经常用到TS评分(Jolliffe et al, 2003)。图 3所示为EFI、MBMA和HDet不同时效取不同的阈值时对淮河流域2012年5—9月暴雨预报的空报率和对应的TS评分，可见，TS评分先随空报率的增大而迅速增大，当空报率达到一定的值后，TS评分达到最大，之后随空报率的增大而减小。但是对于不同的预报时效，MBMA的TS评分最大值都最大，其次是HDet，EFI的TS评分最小，其结果和ROC检验结果一致。

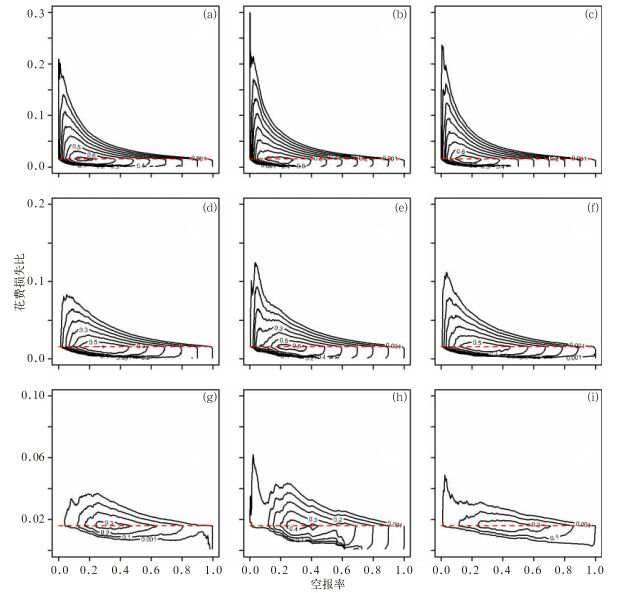
在预报服务，尤其在决策过程中，TS评分并不是唯一的追求目标，决策的做出还要考虑到经济价值。图 4为不同的客观预报方法、不同时效对2012年5—9月淮河流域暴雨预报，在不同空报率和花费损失比时的经济价值，图中画出的最小的经济价值为0.001。可见相对经济价值大于0.001的区域，MBMA大于HDet，EFI的最小，与以上ROC和TS的检验结果一致。对于相同花费损失比的事件，具有正的相对经济价值时，MBMA最大空报率最大，HDet的次之，EFI的最小。对于特定的预报方法和特定的时效，对于大于气候概率的花费损失比，存在一个最大花费损失比r_max。对于某一预报方法，r_max随预报时效的延长而减小，EFI、MBMA和HDet从48~216 h时效的预报，其r_max分别从0.2、0.3和0.24减小到0.04、0.06和0.05(图 4)。对于不同预报方法的同一时效预报，MBMA预报的r_max最大，其次是HDet的，EFI的同样是最小的。

对于大于气候概率o的r值，存在一个最大空报率f_max(r)，空报率必须小于等于这一f_max(r)，此时经济价值为正，当空报率>f_max(r)时，经济价值为负。从以上的分析和图中都可以看出，f_max(r)随r的减小而增大(图 4)。要预报的事件的花费损失比r越大，能容忍的空报率就越小，直到r达到r_max时，对空报率的容忍达到0。

当花费损失比r等于事件的气候概率o时，经济价值达到最大值，与Richardson(2000)的研究结果相符，且此时空报率取0~1之间任意值时，经济价值总是正值。r=o是唯一的空报率取任意值时经济价值都为正值的r值。对于花费损失比r小于气候概率o的事件，此时空报的风险相对于漏报的风险变得非常小，漏报一个事件带来的损失远远大于空报的损失，所以此时对漏报率的容忍变得非常小，而对空报率没有要求。为了把漏报率控制在一定的范围，必然导致空报率会达到一定的值，较小的空报率反而会使经济价值成为负值(图 4)。

3 暴雨预报阈值的选择及预报效果分析

从以上可见，三种方法取不同的阈值对暴雨预报时，所得结果不同。在实际业务应用中，需要定量地确定不同方法不同时效的暴雨预报阈值。

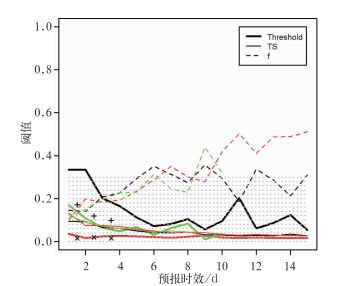
阈值的确定需要首先选择一个标准。预报决策的做出是在命中率和空报率之间寻求平衡，即h尽量大的同时f都尽量小，于是可以以Peirce’s skill score (PSS)最大为标准，即PSS=h-f最大(Jollliffe et al, 2003)。此时MBMA的阈值在0.02，即2%左右，HDet的阈值＜10 mm，EFI的阈值不同时效从0.3减小到0.1左右。10 d以内的预报，随预报时效的延长，EFI、MBMA和HDet的空报率从0.12左右增大到0.3以上，相对于主观预报的0.017左右，增大了一个数量级。此时的TS评分从0.12左右逐渐减小到0.04以下，明显小于主观预报。以PSS最大为标准时，三种方法预报的TS评分和空报率之间没有明显的优劣差异(图 5)。

以业务中应用最广的TS评分(图 3)最大为标准，其阈值相对于PSS最大明显增大，HDet的阈值在25~40 mm，MBMA的阈值从24 h时效的10%减小到360 h时效的4%左右，EFI的阈值从0.6以上减小到0.22左右。72 h时效内的TS评分明显增大。两天内，MBMA和HDet的TS评分接近，大于EFI，3~7 d内，MBMA的TS评分最大，其次是HDet，EFI的TS评分最小，对于9 d以上的预报，MBMA和EFI的TS评分接近。

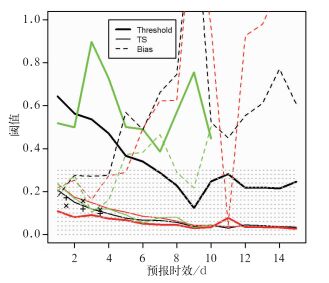
TS评分增大的代价是空报率(图 3)和预报偏差显著增大。EFI的预报偏差从2增大到6左右，MBMA的预报偏差和EFI的接近，HDet的预报偏差从2增大到4，比集合预报小(图 6)。可见，对于ECMWF HDet和EPS，TS评分最大时，预报偏差都显著大于1，暴雨预报范围是实况暴雨范围的2倍以上。

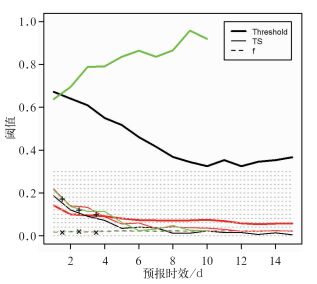
分析中央气象台主观预报可见，对空报率的容忍非常有限，预报偏差略大于1。不同年份5—9月淮河流域暴雨36、60和84 h时效预报的预报偏差差异较小，2012年三个时效的预报偏差的平均值为1.37。如果以预报偏差等于1.37为确定预报阈值的标准，此时的空报率较TS最大且明显减小，各预报方法的阈值进一步增大，HDet的阈值从24 h时效的30 mm以上增大到240 h时效的接近50 mm，MBMA(EFI)的阈值从24 h时效的14%(0.66) 左右减小到360 h时效的接近6%(0.35左右)。不同方法不同时效的空报率都在0.02左右，接近主观预报的空报率0.017。10 d以内的TS评分，EFI最小，MBMA和HDet接近，同时3 d以内预报的TS评分接近或略大于主观预报，10 d以上的TS评分，MBMA大于EFI(图 7)。

可见对于中央气象台目前的预报服务业务，在对空报率的要求下，概率订正后的集合预报和较高分辨率的确定性预报表现出接近的预报效果，但都好于EFI。在接近于1的预报偏差的要求下，EPS相对于HDet的优势较难发挥。

4 结论和讨论

通过对2012年5—9月淮河流域暴雨预报的检验，本文对比了ECMWF较高分辨率的确定性模式(HDet)和集合预报系统(EPS)，其中EPS对比了日降水量的极端预报指数(EFI)和经过改进的贝叶斯模型平均法(MBMA)订正后的暴雨概率。运用了不依赖于模式系统性偏差的ROC检验，对比了TS评分和相对经济价值。并在此基础上，基于不同的标准，计算对比了三种方法对暴雨预报的阈值。得到如下结论：

(1) 在短期时效1~3 d内，由EPS经过MBMA方法后处理所得的暴雨概率预报，与HDet确定模式对暴雨预报的效果接近。到中期时效4~10 d时，MBMA相对于HDet的优势随时效延长而增强，日极端降水预报指数EFI的预报效果最差，可见EPS相对于HDet的优势主要体现在中期时效。

(2) MBMA相对于HDet的优势还体现在预报服务的相对经济价值上，在相同的时效，对MBMA有经济价值的事件的花费损失比，显著大于对HDet有经济价值的事件的花费损失比，对EFI有经济价值的事件的花费损失比最小。

(3) 在不同的标准下确定暴雨预报的阈值，发现在可以容忍的空报率或预报偏差越大的情况下，MBMA相对于HDet的优势越明显，如果将预报偏差限定为主观预报的1.37，此时MBMA相对于HDet的优势减小，两者预报效果接近，可见集合预报的优势主要体现在一个更大的空间范围内通过概率预报的信息，来提高预报服务的相对经济价值。

本文中的EFI指数计算时采用了2007—2011年历史预报资料作为“模式气候”，受资料长度和模式更新等因素的限制，相对于ECMWF最新的由模式回算资料构建“模式气候”，进而计算的EFI指数，会存在一定的差异，这一影响的大小，需要进一步的工作来计算。但是EFI算法的更新和“模式气候”的构建，也从另一个角度证明了集合预报后处理方法对于进一步提高集合预报技巧的作用。