引言

对流有效位能(CAPE)是气块在给定环境中垂直上升时热浮力的垂直积分(李耀东等，1998；Doswell et al，2004)，是判断强雷暴是否能形成的最有用的工具之一(Doswell et al，1994；李娜等，2015)，广泛应用于强对流天气的分析和预报(李耀东等，2004；叶爱芬等，2006；陈子通等，2006；魏东等，2011；赵玉春等，2011；王秀明等，2012；李云静等，2013；张建春等，2014；郑媛媛等，2015)。目前，对CAPE的应用已经扩展到了气候领域，可用于统计对流性降水的时空分布和演变特征、研究气候变化、分析热带气旋的形成和加强、改进模式的对流性降水预报等(Ye et al, 1998; Adams et al, 2009: Riemann-Campe et al, 2009；Molinari et al, 2012；Barkiđija et al，2013)。

CAPE的计算与气块的初始抬升层、气块的温度及温度特性、所取的热力学上升路径、水凝物对密度的影响等有关。因此，CAPE的数值与上述特征关系密切(Craven et al，2002；刘健文等，2007；Vasquez，2009)。除了上述因素对CAPE的影响外，Doswell等(1994)指出：由于CAPE与上升气块和环境的密度差有关，而对密度的准确计算需要用到虚温，因此估计CAPE时也应该使用虚温进行计算。

目前不少省市建立了包括CAPE在内的各种对流参数与强对流之间的关系，用来开展强对流天气有无、天气分类等预报(如雷蕾等，2012；冯民学等，2012；林新彬等，2013；王镇铭等，2013)。但计算CAPE有很多不同的软件或程序，是否使用虚温订正、如何计算虚温订正CAPE并没有统一，导致CAPE数值并不一致、甚至相差很大。MICAPS是我国预报员日常使用的人机交互预报平台，其中内置有CAPE值，它是预报员用于判断强对流天气是否发生以及属于何种类型的重要指标。但是在教学过程中发现，MICAPS中经过虚温订正的CAPE会小于没有经过虚温订正的CAPE。这不但影响了对虚温订正CAPE概念的理解，也给预报员带来了非常大的困惑。仔细查看MICAPS计算CAPE的程序，发现目前在计算虚温订正CAPE时，将自由对流高度(LFC)取为不变，即与虚温订正前相同。这种取法并非个例，GRADS是气象工作者常用的绘图软件，GRADS自带的计算虚温订正CAPE程序中也将LFC取为不变。

虚温订正后的LFC若仍采用订正前的高度，显然与LFC的定义相悖。作为计算CAPE时的积分起点，它的取法不同必然会影响到CAPE的数值。以往的很多文献或教科书(Doswell et al，1994；刘健文等，2007)并没有对虚温订正前后CAPE积分上下限的变化作特别说明，因此很多计算CAPE的软件/程序也忽视了计算虚温订正CAPE时LFC的取法问题，往往设为不变。针对这个问题，本文首先通过理论分析来说明LFC取法不同对CAPE虚温订正造成的影响；并通过实际个例诊断分析说明考虑LFC变化对CAPE计算的影响，以期为MICAPS、GRADS中CAPE虚温订正计算的修正及预报员对虚温订正CAPE的理解提供参考。

1 虚温订正CAPE的理论公式 1.1 常规CAPE与虚温订正CAPE

对流有效位能CAPE常用的表达式为：

$ CAPE = - {R_d}\smallint _{_{{p_{{\rm{LFC1}}}}}}^{^{{p_{_{{\rm{EL1}}}}}}}({T_v} - {\bar T_v}){\rm{dln}}p $

(1)

式中，T_v和T_v分别表示气块和环境的虚温，p_LFC1为自由对流高度，即T_v-T_v由负值转正值的转折点的高度，也即是气块密度开始小于环境密度，气块开始受环境正浮力作功的高度；p_EL1为平衡高度，即T_v-T_v由正值再次转负值的转折点的高度(刘健文等，2007)。

在忽略水汽作用时，式(1) 可写为：

$ CAPE \approx - {R_d}\smallint _{_{{p_{{\rm{LFC2}}}}}}^{^{{p_{{\rm{EL2}}}}}}\left( {T - \bar T} \right){\rm{dln}}p $

(2)

式中，T和T分别表示气块和环境的温度，p_LFC2为不用虚温订正计算CAPE时的自由对流高度，即T-T由负值转为正值的转折点高度；p_EL2为不用虚温订正计算CAPE时的平衡高度，即T-T由正值再次转为负值的转折点高度。

由于现在很多计算CAPE的程序是用式(2) 计算得到，因此我们将之称为常规CAPE。而用式(1) 得到的原始CAPE称为虚温订正CAPE。

可见式(1) 和(2) 中自由对流高度LFC和平衡高度EL是CAPE计算的关键点。查看MICAPS和GRADS中计算CAPE的源程序发现，在用虚温订正方法计算CAPE时，p_LFC1和p_EL1都和用常规方法计算CAPE的p_LFC2和p_EL2相等，即取的是p_LFC1=p_LFC2，p_EL1=p_EL2。这样的取法是否正确？下面先从理论上说明虚温订正前后自由对流高度和平衡高度有何变化。

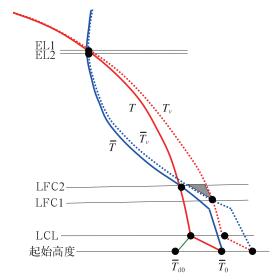
1.2 虚温订正CAPE计算中LFC和EL高度

图 1示意了计算常规CAPE和虚温订正CAPE时的主要特征高度。虚温订正后的自由对流高度记为LFC1，常规的自由对流高度记为LFC2。在LFC2处，由于气块的温度和环境的温度相等，因此T_L2=T_L2(下标L2表示LFC2)。

LFC2高度处的环境虚温和气块虚温分别为：

$ {{\bar T}_{v{\rm{L2}}}} = (1 + 0.608{{\bar q}_{{\rm{L}}2}}){{\bar T}_{{\rm{L}}2}} $

(3)

$ {T_{v{\rm{L}}2}} = (1 + 0.608{q_{{\rm{L}}2}}){T_{{\rm{L}}2}} $

(4)

式中，q_L2和q_L2分别为LFC2处环境大气和气块的比湿。由式(3) 和(4) 可知，LFC2处，T_vL2和T_vL2两者的大小比较取决于q_L2和q_L2的大小。

比湿q的计算公式为

$ q = 0.622\frac{e}{p} $

(5)

式中，e为实际水汽压。一般而言，e≤e_s，e_s为饱和水汽压；q≤q_s，q_s为饱和比湿。饱和水汽压仅是温度的函数，并随温度升高而增加，计算实际水汽压可将露点代入饱和水汽压公式。

由式(5) 可得环境大气的比湿为

$ {{\bar q}_{{\rm{L}}2}} = 0.622\frac{{{{\bar e}_{{\rm{L}}2}}}}{{{p_{{\rm{LFC2}}}}}} $

(6)

而对于气块而言，LFC2处已经饱和，因此

$ {q_{{\rm{L}}2}} = {q_{s{\rm{L}}2}} = 0.622\frac{{{e_{s{\rm{L}}2}}}}{{{p_{{\rm{LFC}}2}}}} $

(7)

下面分两种不同的情况考虑：

(1) 当LFC2处环境的温度露点差为0时，e_L2=e_sL2，考虑到LFC2处气块与环境的温度相等，因此两者的饱和水汽压相等，e_sL2=e_sL2，因此T_vL2=T_vL2。那么经过虚温订正后的LFC与常规方法算得的LFC高度相同，即p_LFC1=p_LFC2。

(2) 当LFC2处的温度露点差>0时，e_L2 < e_sL2，则T_vL2 < T_vL2。那么经过虚温订正后的LFC低于常规方法算得的LFC，则p_LFC1>p_LFC2，如图 1所示。

通常是第二种情况。也就是说，虚温订正后，自由对流高度多数情况下会下降。图 1中，EL1和LFC1之间红色和蓝色虚线所围面积代表的是虚温订正CAPE，而图 1灰色阴影区表示的即是第二种情况下，考虑与不考虑LFC变化时CAPE的差异。

从图 1也可以看到，当图中的LFC1和LFC2高度不变且虚温订正后气块的状态曲线不变时，阴影区的面积与LFC2高度上T_v-T_v的大小有关。定性而言，T_v-T_v越大，阴影区面积越大。根据式(3) 和(4) 以及T_L2=T_L2，可得

$ {T_{v{\rm{L}}2}} - {{\bar T}_{v{\rm{L}}2}} = 0.608{T_{{\rm{L}}2}}({q_{{\rm{L}}2}} - {{\bar q}_{{\rm{L}}2}}) $

将式(6) 和(7) 代入上式得

$ \begin{array}{l} {T_{v{\rm{L}}2}} - {{\bar T}_{{\rm{vL2}}}} = C{{\bar T}_{{\rm{L}}2}}\left( {\frac{{{e_{s{\rm{L}}2}}}}{{{p_{{\rm{LFC}}2}}}} - \frac{{{{\bar e}_{{\rm{L}}2}}}}{{{p_{{\rm{LFC}}2}}}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{C{{\bar T}_{{\rm{L}}2}}}}{{{p_{{\rm{LFC2}}}}}}[{e_s}({{\bar T}_{{\rm{L}}2}}) - {e_s}({{\bar T}_{d{\rm{L}}2}})] \end{array} $

(8)

式中，C为常数，C=0.608×0.622，T_dL2为LFC2处的环境露点。通过上式可知，当LFC2处环境空气的温度露点差越大时，则T_v-T_v也越大。也就是说，在其他条件相同的情况下，原LFC高度上环境空气越干，则由于LFC取法不同造成的虚温订正CAPE之差越大。反之，如果原LFC高度上环境空气越湿，则由于LFC取法不同造成的虚温订正CAPE之差越小。

下面再看一下平衡高度EL的变化。记虚温订正后的EL高度为p_EL1，常规方法计算的EL高度为p_EL2。在p_EL2处，由于气块的温度和环境的温度相等，因此T_E2=T_E2(下标E2表示EL2)。该高度上环境虚温和气块虚温分别为：

$ {{\bar T}_{v{\rm{E}}2}} = (1 + 0.608{{\bar q}_{{\rm{E}}2}}){{\bar T}_{{\rm{E}}2}} $

(9)

$ {T_{v{\rm{E}}2}} = (1 + 0.608{q_{{\rm{E}}2}}){T_{{\rm{E}}2}} $

(10)

${{\bar q}_{{\rm{E}}2}} = 0.622\frac{{{{\bar e}_{{\rm{E}}2}}}}{{{p_{{\rm{EL2}}}}}} $

(11)

$ {q_{{\rm{E}}2}} = {q_{s{\rm{E}}2}} = 0.622\frac{{{e_{s{\rm{E}}2}}}}{{{p_{{\rm{EL}}2}}}} $

(12)

到了高层，水汽稀少，不论是环境大气的实际比湿q_E2还是气块的饱和比湿q_sE2都非常小。

与式(8) 类似，式(10) 和(9) 相减，并将式(11) 和(12) 代入可得

$ \begin{array}{l} {T_{v{\rm{E}}2}} - {{\bar T}_{v{\rm{E}}2}} = C{{\bar T}_{{\rm{E}}2}}\left( {\frac{{{e_{s{\rm{E}}2}}}}{{{p_{{\rm{EL}}2}}}} - \frac{{{{\bar e}_{{\rm{E}}2}}}}{{{p_{{\rm{EL}}2}}}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{C{{\bar T}_{{\rm{E}}2}}}}{{{p_{{\rm{EL}}2}}}}[{e_s}({{\bar T}_{{\rm{E}}2}}) - {e_s}({{\bar T}_{d{\rm{E}}2}})] \end{array} $

(13)

通常情况下，e_s(T_E2)>e_s(T_dE2)。即在EL2处，气块虚温仍高于环境虚温，因而订正后的EL1高于常规方法得到的EL2，即p_EL1 < p_EL2(如图 1所示)。但由于高层的水汽含量极少，式(13) 的值非常小，因此可认为EL在订正前后没有明显变化，近似相等，它的取法对虚温订正CAPE的影响可以忽略。

2 实际分析示例

目前MICAPS计算的CAPE包括常规CAPE和LFC不变的虚温订正CAPE，这些值都是自动输出，不便修改源程序。因此本文的实际分析示例中采用GRADS软件，按上节的方法来计算虚温订正CAPE(注：GRADS软件中缺省的虚温订正CAPE没有考虑LFC的改变)。

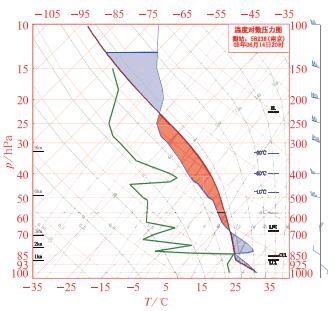
首先，对比MICAPS和GRADS两种软件绘制的T-lnp图以及计算的一些相关物理量是否存在显著差异。选取2005年6月14—15日的一次强对流个例作分析。2005年6月14日晚到15日凌晨，安徽东北部、江苏北部出现了强对流风暴，造成特大雹暴灾害。强对流风暴自西北向东南方向移动，14日夜间影响安徽的宿州、蚌埠、滁州等市，15日02:50移出安徽省进入江苏，南京、徐州等多地相继发生冰雹和暴雨灾害。在强对流发生前的14日20时，安徽和江苏的多个探空图显示具有很强的不稳定能量。其中南京的探空显示CAPE较大，且具有第1.2节中提到的虚温订正前LFC高度处环境大气较干的特征(图 2)。

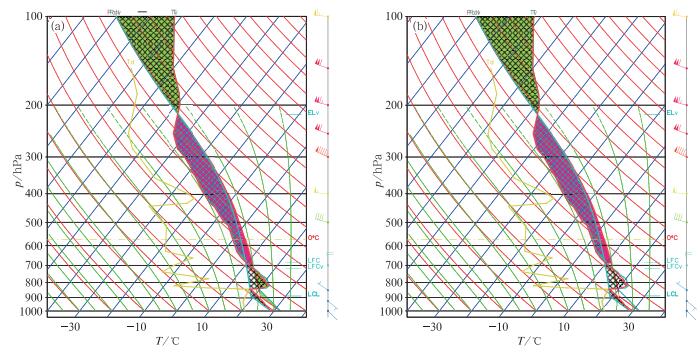
图 3是利用GRADS软件绘制的斜T-lnp图，图上包含了常规方法和虚温订正方法得到的能量区、主要特征高度等信息。GRADS利用常规方法绘制的CAPE区及主要交点与MICAPS绘制的基本相当，形状也一致，但数值有一定差异(见表 1)。MICAPS的常规CAPE为1358.5 J·kg^-1，而GRADS计算的常规CAPE为1563.5 J·kg^-1，GRADS比MICAPS计算的常规CAPE大了约200 J·kg^-1。CAPE数值的差异可能与采用的热力学近似公式(尤其是湿绝热线的计算)的差异有关。仔细比对发现，在同样高度的LCL处GRADS对应的湿绝热线比MICAPS偏右一些。GRADS得到的LFC较MICAPS的LFC略低5 hPa，而EL的情况相反，略高10 hPa。于是相比MICAPS而言，GRADS根据公式(2) 计算常规CAPE时，下限降低而上限升高，且由于状态曲线略右偏，积分区间内，气块的温度也略偏高，使得整个积分值偏高，CAPE偏大。

虽然两个软件之间对流参数的具体数值有一些偏差，但是总体而言斜T-lnp图相似。下面采用GRADS软件按上节的公式来计算LFC不变与变化时的虚温订正CAPE。图 3a是严格按照定义(LFC变化)计算虚温订正CAPE的斜T-lnp图，图 3b是LFC取为不变时计算虚温订正CAPE的斜T-lnp图。如图 3和表 1所示，LFC在虚温订正后降低，从683.6 hPa降低到716.5 hPa，LFC处的温度升高了3.8℃。EL高度在虚温订正后略有升高，气压从215.3 hPa变为215.1 hPa，其变化可以忽略。

前面我们提到，很多软件(包括MICAPS和GRADS)，在计算虚温订正CAPE时，采用的积分上下限LFC和EL的高度与计算常规CAPE时一样。那么LFC变与不变会造成CAPE数值上有多大的变化呢？利用GRADS软件，通过计算LFC不变时的虚温订正CAPE(见表 1)，发现CAPE由1746.7 J·kg^-1降低为1734.5 J·kg^-1，减少了12.2 J·kg^-1。虽然考虑了LFC变化的虚温订正CAPE与LFC不变得到的虚温订正CAPE相比增加值并不是太多，但是比较图 3可以看到，它在图形上的表示更加合理，可以确保LFC的高度是气块虚温与环境虚温之差由负值转为正值的转折点高度，物理意义更加清晰。

3 结论和讨论

MICAPS和GRADS是预报员常用的两种用来计算某地CAPE大小的软件。但是目前两种软件在计算虚温订正CAPE时，都没有考虑LFC的变化。本文从理论分析和实例计算来说明虚温订正CAPE的正确求解方法，得到了以下结论：

(1) MICAPS虚温订正CAPE的求算方法存在原则错误。从理论角度可以证明，考虑虚温订正后，LFC会降低，而EL基本不变。在一般情况下，考虑LFC降低计算的虚温订正CAPE会比采用LFC不变的虚温订正CAPE大。

(2) 尽管实例分析表明，考虑了LFC变化的虚温订正CAPE比起LFC不变得到的CAPE增加并不是太多，但是它在图形上的表示更加合理，物理意义更加清晰。可以确保LFC的高度是气块虚温与环境虚温之差由负值转正值的转折点高度。

(3) 目前很多省在利用一些对流参数来开展统计研究，CAPE的计算偏差会影响阈值选取的准确性。在使用过程中不但要注意到虚温订正CAPE计算中LFC高度是否改变，同时还要注意抬升气块取法等信息。

致谢：本文写作过程中恰逢Doswell先生来气象干部培训学院讲学，就虚温订正CAPE的求算方法问题与之进行了讨论，在此表示谢意！