引言

浙江省拥有较长的海岸线和丰富的渔业资源，海洋经济在浙江经济建设中占据着重要的地位。为了建设海洋强省，近几年浙江省政府又提出了加强海洋建设和发展海洋经济的新要求，气象部门也应顺应形势发展，为社会相关部门提供更高质量的海洋气象服务产品。海面风场的精细化监测和预报是当前海洋气象服务的重要内容，而两者的高质量实现均有赖于获得准确的海面风场实况。由于海上浮标站的布设和维护成本较高，因此目前浙江省气象部门布设的浮标站点仅有舟山浮标和温州浮标两个点，且其布设位置靠外，很难有效反映沿岸一带海域，尤其是舟山群岛和杭州湾海域内的风场情况。当然可以使用卫星反演的海面风场资料作为实况，如欧洲卫星气象组织的ASCAT(Advanced SCATterometer)海洋风场产品，该资料在国外已经得到了很好的研究和应用，国内气象部门也在逐步开展该资料的应用(高留喜等，2014)。然而此类卫星资料在国内应用中的最大问题在于，对离岸较近的海域，其反演质量并不高，这主要是因为沿岸地形会增大浪高，进而扩大反演误差。张增海等(2014)对此类ASCAT资料的误差统计表明，风速的平均偏差和平均绝对误差都达到了4.9 m·s^-1，均方根误差也在3.7 m·s^-1，如此大的误差使其很难在实际业务中得以应用。另外卫星数据的时间精度并不是很高，这也是其在业务应用中的欠缺之处。

近年来浙江气象部门布设了一定数量的海岛和滩涂中尺度气象站，这些自动气象观测站可以监测海域内风场的大致状况，但是由于海岛站有一定的海拔高度，观测到的风场与海岛附近的实际海面风场存在一定的差异，因此有必要将海岛站上的观测风场反推到海面上，然后再应用客观分析的方法，将离散点转换到网格点上，从而实现海面风场的精细化监测。之前的气象学者主要使用近地面风廓线理论推算离地面某一高度处的风速(傅抱璞等，1981)，本文与之略有不同，同样运用该理论，但依据一定海拔高度上的海岛站风速来推算附近海面上的风速。

1 梯度风的位置及变化特征分析 1.1 风塔的分布

目前浙江北部沿岸地区已布设了一定数量的风塔站(图 1a中三角)，考虑到数据可靠性以及站点代表性，本文选取大渔山、佛渡、上虞以及慈溪四个风塔站来分析各自风速廓线的变化特征。大渔山风塔建在舟山大渔山岛上，海拔高度为60 m，其风塔观测数据对于舟山地区海岛附近一定高度上的风场具有较好的代表意义。佛渡站位于舟山佛渡岛上，海拔高度80 m，由于其处于大陆和其他岛屿的包围之中，因此可用其风塔观测数据来近似代表靠近大陆的岛屿间狭窄海域内一定高度上的风场情况。慈溪站位于杭州湾南岸的滩涂上，海拔高度为3 m，其风塔观测数据对于杭州湾南岸滩涂和邻近海域内的风场具有一定的代表意义。上虞站位于杭州湾喇叭口内侧的滩涂上，海拔高度也为3 m，其风塔观测数据能较好地代表杭州湾内侧海域内的风场(图 1a)。

1.2 风向风速的季节变化

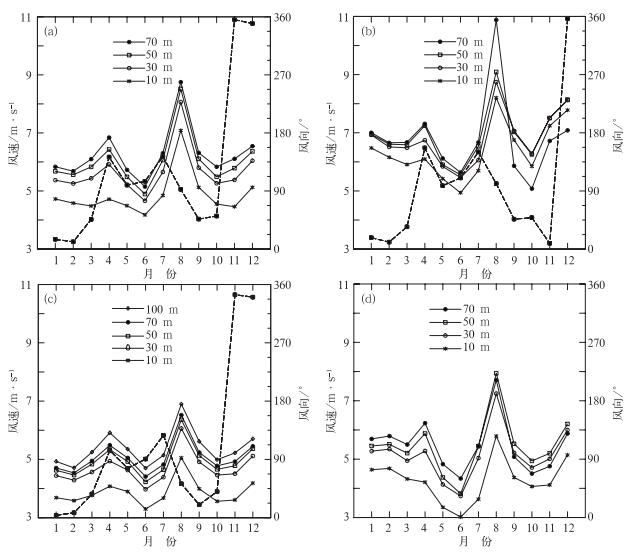
本文使用2012年的逐小时梯度风资料来分析慈溪、大渔山、上虞和佛渡四个风塔站近地面层风向(佛渡站缺风向资料)、风速的季节变化情况(图 2)。可以看到各站风向的总体变化趋势较为一致，冬季由于多冷空气活动，因此以偏北风为主，其中12月多西北风，1、2月多东北风。3月处于季节转换，偏东风分量逐渐增加，4月慈溪站和大渔山站的偏南风明显增加，可能与其处于入海高压后部有关。5—6月，受气旋活动影响，各站盛行偏东风。7月各站以东南风为主，这可能与夏季海陆热力差异引起的环流有关。8月随着副热带高压(简称副高)脊线位置北抬，转为偏东风，但上虞站却以东北风为主，这可能与其所处的地理位置有一定的关系，从图 1a中可以看到上虞站位于杭州湾喇叭口内侧偏南的位置上，偏东气流经过宁波慈溪地区后往往有所减弱，而海陆热力差异可能使该地的偏北风风量有所增加。9—10月处于秋、冬季转换之际，各站均以东北风为主。从上述分析可以看到，杭州湾及舟山近海海域风向的季节变化主要由各类天气系统所主导，但该地区独特的地形及海洋效应也对风向有一定的影响。

四个塔站中除了上虞站有5层观测高度以外，其余皆为4层。和风向的季节变化类似，各站各层风速的总体变化趋势较一致。平均最大风速出现在8月，这是由于副高脊线位置偏北，其南侧热带系统的活动范围明显向北扩展，该地区的南北向气压梯度加大，因此风速较7月出现了明显的跃升。冬季和初春也是风速相对较大的季节。10~30 m风速差明显要大于30 m以上邻近层之间的风速差，这是因为尽管这些塔站位于滩涂或是岛屿上，但是10 m处的风场受下垫面影响仍较大，而30 m以上的风场受下垫面的影响明显减小，更加接近海面以上同高度风场。9月起大渔山站和佛渡站70 m高度处的风速比低层的还要小，这可能由于高层比低层降温更明显，大气处于不稳定层结状态，高层动量损失要大于低层所致，相比而言大渔山站高层风速损失更加明显，这说明其低层大气受海洋的影响更大。

2 近地面风廓线率及其计算方法 2.1 风廓线理论简述

在研究风速廓线的变化时许多研究机构或学者(海洋石油研究所工程试验室等，1978；傅抱璞等，1981；植石群等，2001)多采用指数律公式

$ \mathit{U} = {U_1}{\left({\frac{\mathit{z}}{{{\mathit{z}_{\rm{1}}}}}} \right)^\alpha } $

(1)

或对数律公式。

$ \mathit{U} = {\mathit{U}_{\rm{1}}}\frac{{\ln \mathit{z} - \ln {\mathit{z}_0}}}{{\ln {\mathit{z}_{\rm{1}}} - \ln {\mathit{z}_0}}} $

(2)

通过上式就可以依据某个高度z₁上的实测风速U₁来求得另一高度z上的风速值U，式中α和z₀是需要确定的参数，如何确定好这两个参数至关重要，将直接影响到反演风速的准确性。指数律中参数α主要由下垫面粗糙度、大气层结状态及风速大小所决定。对数律中的参数z₀应是平均风速等于零的下垫面的粗糙高度，而对于特定的下垫面而言，只要地面情况不改变，它的粗糙高度是不变的，因此一般适用于近似中性层结的大气，但是这些限定给实际计算造成诸多不便，因此通常也将z₀看作为由下垫面粗糙度、大气层结状态及风速大小决定的动态参数。之前的气象学者(傅抱璞等，1981；植石群等，2001)对两种边界层风廓线率的研究表明，总体而言无论下垫面是陆面还是水体，使用指数律计算得到的风速误差要小于对数律，因此本文将采用指数律来反演海面风速，并选用30和70 m高度上的平均风速来确定指数律参数α的值。

2.2 两类指数律参数α的计算

为了深入研究在不同的下垫面条件下参数α随季节和风速的变化特征，本文将计算以下两类α。第一类α中依据风廓线样本的采集时间采用分月处理的方法，由各月30和70 m高度上的平均梯度风数据代入式(1) 中计算得到该月的α，其值主要反映大气层结状态的季节变化对于参数α的影响。第二类α中依据风廓线样本30 m高度上的梯度风数据采用分组处理的方法，即将15 m·s^-1以下风速分为15组，每组的间隔为1 m·s^-1，15 m·s^-1以上不分组，对所有风廓线样本进行分组归类处理以后，计算每组中30和70 m上的平均梯度风，并将其带入式(1) 中得到该组的α，其值反映的是风速大小对于参数α的影响。

2.3 指数律参数α的变化特征分析

针对四个风塔站计算相应的指数律参数α，其各月的变化情况如图 3a所示。可以看到2—4月，各站的α值出现较明显的增加，这是由于随着冬、春季节转换，上层大气出现较明显回暖，而地面层受水体影响，回温有所滞后，大气稳定度变大。7—8月，除了大渔山站之外，其他站的α值均出现一定程度的下降，从站点分布图上(图 1a)可以看到这些站点受陆地影响更为明显，夏季地面层气温往往较高，因此白天大气稳定度较小，而大渔山站四周海域较为开阔，受海洋影响更为明显，白天近地面层气温上升缓慢，因此其大气稳定度相对较大，因此α值出现了明显增加。9月大渔山和佛渡两个海岛站的α值出现了非常明显的下降，这是因为地面上层大气随着冷空气渗透，温度出现下降，而海岛站的近地面层受海洋影响，温度下降滞后，因此大气稳定度迅速变小，上层风场动量损失明显，导致α出现负值。9—11月上虞和慈溪两个滩涂站的α值则是逐渐增加，这是因为这两个站受陆面影响较为明显，地面层温度下降较快，而上层大气气温下降相对滞后，致使大气稳定度变大。以上分析表明，α值的改变与由季节变化和下垫面热力特性引起的大气稳定度的变化密切相关。

图 3b是四个风塔站的指数律参数α随风速的变化情况，可以看到当风速小于1 m·s^-1，即弱风状态下时，α都到达了最大值，其中佛渡站超过了0.9，说明一般大气在极稳定的条件下，风速梯度较大，但大渔山站的情况有所不同，其α值接近0，表明弱风情况下风速梯度不明显。当风速大于1 m·s^-1，各站的α值都出现了不同程度的下降，说明随着风速的增大，湍流交换在增强，致使风速梯度减小，而佛渡站和大渔山站都出现了负值，说明这两个站的湍流交换更强，导致上层大气动量损失明显，从图 2a中可以看到这种情况主要出现在9—12月。当风速增大到一定程度以后，各层空气充分混合，α也趋向于一个与风速无关的稳定值。

3 海面风场反演方法及其准确性分析 3.1 反演方法及参数α的适用性分析

本文中海面风场反演的思路是首先选取合适的海岛中尺度自动站，然后依据相应的风速廓线将海岛观测风速反推到海面高度上，作为海岛附近海面的近似风速，最后使用基于径向基函数的Multiquadric算法(何斌等，2014)将离散分布的海面风速近似值转换到中尺度网格点上，从而实现海面风场的精细化监测。实现过程中比较关键的是如何选择合适的海岛站以及与之匹配的风速廓线，因为这将直接影响到反演海面风场的准确率。从之前对于指数律中参数α的分析可以看到，该参数是随月份而发生变化的，且对于同一月份而言，不同位置上的参数α也表现出一定程度的差异，上虞站和慈溪站由于都位于滩涂之上，而且海拔高度相同(均为3 m)，下垫面状况相近，因此参数α的变化规律及值的大小较为接近。佛渡站和大渔山站的风速廓线与前两站则表现出较大的不同，特别是在8月以后，这与其属于海岛站有关，下垫面的水体特征表现得更加明显。另外需要注意的是这两个站的海拔高度都较高(佛渡站的高度为80 m，大渔山站的高度为60 m)，这样其观测值代表的是一定高度上的风廓线变化状态。从这两个站梯度风速的季节变化可以看到(图 2b和2d)8月以后，30~50 m风速增加非常缓慢甚至不增加，50~70 m风速随高度反而呈不同程度的减小，此种现象在大渔山站表现得更为明显。这说明在海面上空一定高度以下，风速随高度增加，而在该高度以上动量损失明显风速随高度减小，当然这种情况主要出现在秋、冬两个季节，这里大致估算该高度出现在120 m左右，因此在反演海岛中尺度站的风速时，直接使用佛渡站和大渔山站的风廓线变化率是否合适将通过以下试验来进一步论证。

3.2 试验数据及参数α的确定

如何自前述4种具有一定代表性的风速廓线中，选择适合海岛风场反演的参数α，需要通过对反演误差的比较来予以确定，而该误差的理想校对标准即为浮标站，但由于舟山地区仅有舟山浮标一个外海站点，不适合进行内海海域的对比分析，因此选用上海提供的航道浮标和黄泽洋船标来分析误差，这两个标站位于岛屿间的海域内，能够较好地代表内海海域的海面风场特征(图 1b)。试验区域如图 1b所示，试验数据的时间范围为2013年8月1日00时(北京时，下同)至2014年10月20日00时，采样间隔为1 h，分析要素为10 min平均风速，如此理论样本数将达到21362，但是由于上海提供的标站数据并不完整，因此实际样本数要少于该数量。从2.3节的分析可以看到，指数律参数与季节和风速都有一定的关系，但是需要指出的是随着风速的增大，动力湍流作用会逐渐增强，从而导致大气层结不稳定度增大，风速梯度减小，α值也逐渐减小并趋于稳定，也就是说风速与大气层结状态之间是存在着一定的联系的。而傅抱璞等(1981)也曾指出当风速较小时，大气层结对指数律参数的影响较大，但当风速达到一定值以后，指数律参数的变化将非常缓和，因此本文将使用反映大气层结季节变化的月平均指数律参数α来反演海面风速场，但首先将通过计算各风塔站50 m高度上反演风速的均方根误差(图 3c)来验证参数α的有效性，验证数据仍为2012年逐小时的梯度风资料。可以看到6月前各风塔站的均方根误差均不超过0.6 m·s^-1，6月后上虞站和慈溪站的变化仍较平稳，而佛渡站和大渔山站均出现较为明显的波动上升趋势，其中佛渡站误差相对较小，基本上都在1.0 m·s^-1以下，而大渔山站8月和12月的均方根误差接近1.5 m·s^-1。对比图 2b, 2d可以看到8月以后，佛渡站和大渔山站70 m高度上的平均梯度风反而要小于50 m高度上的风速值，而指数律参数α是使用30和70 m的平均梯度风获得的，因此由其反演得到的50 m高度上的风速值与实况值的误差将有所增大。此外可以看到大渔山站8月70 m高度上的平均梯度风值明显大于50 m高度上的风速值，这也是导致大渔山站8月误差明显增大的原因。上述分析说明对于风塔站上的梯度风反演而言，月平均指数律参数α是有效的，但由于下半年海岛风塔站上空风速廓线的变化特征并不一致，因此其误差相应有所增大。

3.3 统计方法

本文使用以下三种统计方法：

平均偏差

$ ME = \sum\limits_{i = 1}^n {\left({\mathit{Ai} - \mathit{Bi}} \right)} /\mathit{n} $

(3)

平均绝对误差

$ MAE = \sum\limits_{i = 1}^n {|\mathit{Ai} - \mathit{Bi}|} /\mathit{n} $

(4)

均方根误差

$ RMSE = \sqrt {\sum\limits_{i = 1}^n {{{\left({\mathit{Ai} - \mathit{Bi}} \right)}^2}} /\mathit{n}} $

(5)

上式中的误差统计是在浮标站点上进行的。A为反演得到的浮标站(图 1b中空心圆点)风速，具体计算方法为：首先将海岛中尺度自动站(图 1b中实心圆点)观测风依据风廓线理论反演到海面上，其坐标位置同该海岛站，再使用客观分析方法将这些离散的反演风速值网格化，然后使用网格化的反演风速场插值获得浮标站反演风速。B为浮标站观测的风速，n为样本数。

3.4 统计结果分析

表 1为使用4种不同风速廓线得到的三类统计误差。可以看到对于总体样本而言，使用佛渡风廓线率得到的平均偏差(ME)最小，为-0.5 m·s^-1，而上虞风廓线率得到的平均绝对误差(MAE)和均方根误差(RMSE)最小，分别为1.55和2.09 m·s^-1，而使用大渔山风廓线变化率得到的MAE和RMSE反而是最大的，ME也较大。从大渔山站的位置可以看到，它属于海岛站，其风速廓线本应更适合海岛站的风速反演，但正如前面分析的，其观测值代表的是60 m高度以上的风廓线变化状态，而上虞站下垫面虽然与海岛站差别较大，但其海拔仅3 m，因而其观测值代表了100 m以下的风廓线变化状态，与多数海岛站的反演高度较为一致。佛渡站虽然也属于海岛站，但其更靠近大陆沿岸，四周海域狭窄，其下垫面特征更加接近滩涂站。试验结果表明总体而言大气层结状态较下垫面状态对风速反演的影响更大。表 1中还列出了分月的误差统计数据，可以看到尽管使用大渔山风速廓线的总体误差较大，但1—6月得到的ME、MAE和RMSE最小，说明1—6月大渔山风速廓线用于风速反演是合适的，1—6月大渔山指数律参数α为正值，且与其他风速廓线的总体变化趋势较为一致(图 3a)，说明海面上高层和低层的大气稳定度接近。但从7月开始，大渔山风速廓线的误差逐渐增大，到10月误差达到最大，ME为5.75 m·s^-1，MAE为5.94 m·s^-1，RMSE为7.15 m·s^-1，而指数律参数α从9—12月一直都为负值，且在10月出现最小值，说明这段时间内海面上高层和低层的大气稳定度差异较大，大渔山站的风速廓线无法较好地反映海面上低层大气的稳定度，因此误差迅速增大，而该时段内其他风塔站的风廓线率的代表性则要好很多，尤其是佛渡风廓线率，其误差几乎是最小的。以上分析表明在进行海岛风速反演时，需要同时考虑下垫面的状况和风速廓线的季节变化特性，因此目前很难选取单一一种风廓线率用于风速反演，而需要分季节使用风廓线率，1—6月可以使用大渔山风廓线率，而7—12月可以使用佛渡风廓线率。基于此方案又进行了总体样本试验，得到的ME为0.04 m·s^-1，MAE为1.51 m·s^-1，RMSE为2.01 m·s^-1，说明使用该混合风廓线率计算得到的反演风场几乎无系统性偏差，而MAE和RMSE也小于任一单一风速廓线。

虽然混合风廓线率综合考虑了下垫面和大气层结的影响，具有较低的统计误差，但要将其业务化仍存在一些问题：风廓线率试验中使用的海岛中尺度自动站(图 1b中实心圆点)是不是最优的选择，即上述的统计误差是不是最小的；此外风廓线率是有一定区域特征的，这是否表明由海岛中尺度自动站反演得到的有效海面风场仅局限于海岛附近，为此本文进一步开展了海面风场反演优化和影响范围的试验。该试验设置和前面风廓线率试验的设置基本一致，为了验证离浮标站最近的三个海岛站黄泽山、鼠浪湖和白节对反演风速场的影响，进行了7组试验，每组试验从风廓线试验所选海岛站中去除1~3个海岛站，具体组合如表 2所示。可以看到在去除1个海岛站的试验中，黄泽山站的去除使得试验误差相比风廓线率试验有一定的减小，其ME值和RMSE值分别为1.41和1.85 m·s^-1，而去除鼠浪湖或白节站使得误差反而略有增大。这说明虽然黄泽山站离浮标站距离较近，但该站实际风速廓线的变化与混合风廓线率存在一定的差异，致使其反演的风速值反而使得浮标站的反演质量有所下降，鼠浪湖、白节站对浮标站反演风速的影响也并不明显。在去除两个海岛站的试验中，黄泽山和白节站试验误差出现了进一步的下降，MAE和RMSE分别为1.30和1.70 m·s^-1，而其他两组试验误差则较风廓线试验略有上升。当去除三个海岛站时，试验误差达到了最小值，MAE和RMSE分别为1.28和1.68 m·s^-1。自上述分析可以发现，对于浮标站反演风场而言风廓线率试验中得到的误差并非最优。通过去除部分海岛站可以提高反演风场的质量，但去除哪些海岛站并没有明确标准，主要还是通过计算实际的统计误差来确定。可以看到去除黄泽山、鼠浪湖、白节单站的RMSE分别为1.85、2.10和2.05 m·s^-1，而去除这三个站后的RMSE则为1.68 m·s^-1，明显小于去除任何单站的RMSE。这说明在去除海岛站之后，浮标站附近的反演流场会产生非线性的改变，因此统计误差也表现出一定的不连续性。从上述试验结果可以看到，离浮标站较近的海岛中尺度自动站对附近海面风场的反演效果并不如预期的理想，而使用离浮标站较远的海岛中尺度自动站反而获得较高质量的浮标站附近的海面风场，这一方面可能是因为对于某个海岛站而言，混合风廓线率仍不能非常准确地反映其下垫面和大气层结状态；另一方面由于海面相对陆面而言下垫面较为均一，因此海岛站的反演风速的实际影响范围要更大，从图 1b中大致估计有效影响范围至少可以达到30 km。

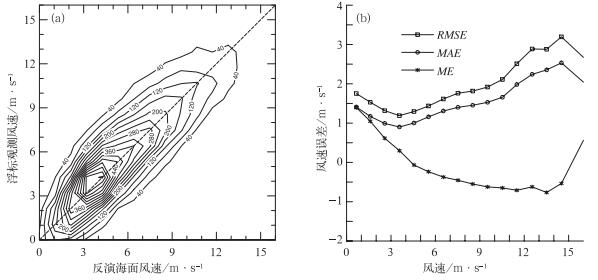
图 4a为使用混合风速廓线得到的海面反演风速和浮标观测风速散布图，可以看到样本频次等值线几乎以虚线为对称轴，这也说明系统性偏差较小。对所有样本风速按1 m·s^-1的间隔进行分级统计后发现(图 4b)，RMSE和MAE的变化曲线基本一致，只是RMSE较MAE略大，当风速较弱时(小于3 m·s^-1)，误差随着风速的增大而减小，当处于中等或较强风速段时(大于4 m·s^-1且小于11 m·s^-1时)，误差随着风速的增大而缓慢增加。而当风速大于11 m·s^-1时，误差增长较为明显，RMSE的最大值达3.2 m·s^-1，此后随着风速的进一步增大，误差又出现回落。偏差的变化则有所不同，当风速较弱时，ME均为正值，说明反演风速略大于观测风速。而当风速大于4 m·s^-1，ME均为负值且有逐渐减小的趋势，说明随着风速的增大，反演风速反而要低于观测风速，但当风速大于15 m·s^-1时，ME再次变为正值。从图 4a也可以看到样本风速主要集中在11 m·s^-1以内，而该风速段内的RMSE小于2.1 m·s^-1，MAE小于1.66 m·s^-1，ME也在0线上下变化，这说明总体而言使用混合风廓线率得到的反演风速场还是有效的，只是在强风速下(平均风速大于6级)，误差会有所偏大。由于本文在计算风廓线率时使用了平均风速，这可能使得该风廓线率对大风速的适用性变差，因此可以考虑分别计算各级风速上的风速廓线，以提高大风速段上的反演准确率。

3.5 个例分析

为了将上述风场反演方法应用于实际海面风场的计算并验证其准确率，本文选取了2014年5月10—11日对我国中东部地区有明显影响的气旋个例进行分析。反演算法中海岛或滩涂自动站(图 1a中实心圆点)的风速廓线的确定原则是：对于周围海域面积较为开阔的海岛站，选择前述的混合风廓线率，其他中尺度自动站则依据下垫面的状况选择合适的塔站风速廓线。

3.5.1 天气概况

2014年5月10日08时500 hPa上高原东侧30°N以南地区有暖性低槽东移，中低层有气旋性低涡发展，而在40°N以北的蒙古境内有冷性低涡槽活动，我国河西走廊地区处于槽底，北槽的位相略落后于南槽。11日08时南槽在东亚大陆沿岸脊后西南偏南气流的引导下向东北方向移动，而北槽在槽后较强冷平流的作用下加深加强，移动速度慢于南槽。中低层低涡也在高空引导气流作用下向东北方向强烈发展，低涡的西北侧开始有冷空气侵入。11月20日南槽在向东北方向移动的过程中逐渐并入北槽前的西南气流中，致使北槽进一步加强，但由于其主体位置偏高，因此冷空气对浙江北部沿海的影响并不明显(图略)。

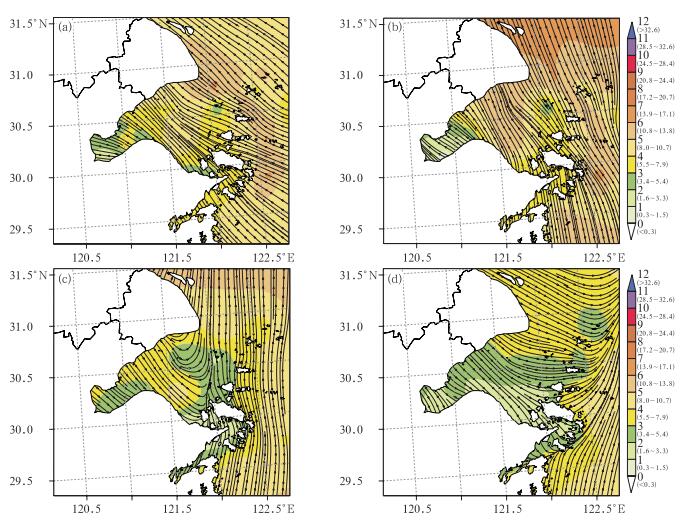
3.5.2 海面风场演变特征分析

10日20时浙江北部沿海处于低涡前部的东南气流中(图 5a)，一条6级以上的大风速(10 min平均风速，下同)带穿越舟山群岛东侧和北侧岛屿，舟山主岛附近风速较小，在4级左右。杭州湾海面自外向内风速逐级减小，内侧风速仅有2~3级。11日08时随着低涡北上，浙江北部沿海处于低涡底部，从图 5b中可以看到偏南风明显加大，舟山群岛以北风速在7级以上，舟山主岛两侧风速较大达到了6级，主岛附近风速仅在4级左右，杭州湾内的风速减弱明显。11日16时随着低涡北上，其后部的西北气流扩散到海面上，舟山主岛左侧附近可以看到一条明显的气流辐合线，风速也较之前有明显减弱，浙江北部近海风力在3~4级(图 5c)。11日20时浙江北部近海已完全为西北气流控制，风力进一步减弱(图 5d)。

表 3为本例中3个不同时次上浮标站点的观测值(10日20时无资料)和反演值的实际差异，可以看到总体而言两者间的误差不大，只是16时航道浮标和19时黄泽洋船标的误差偏大，都达到了2.7 m·s^-1。分析16时的海岛站风速数据可以发现，离航道浮标最近的白节站(高度97 m)和黄泽山站(高度96 m)的风速分别为8.7和7.5 m·s^-1，按照海岛站5月的风速廓线推算航道浮标处的风速不应超过海岛站的风速，但实际情况却相反，此外，19时黄泽洋船标的观测值较反演值要明显偏小。出现上述情况一方面可能是因为所使用的风速廓线反映的是大气层结的月平均状态，而实际大气层结状态是存在一定的波动，从而导致某一时次反演风场的误差增大，另一方面也可能是因为海面上一些甚小尺度系统引起风场的异常变化，而海岛自动站没有捕捉到这些细微的变化特征。

4 结论

本文首先分析了大渔山、佛渡、上虞、慈溪四个风塔站的风向风速和风廓线的变化特征，并基于此利用不同的风速廓线变化率开展海面风速反演试验，结果表明：

(1) 尽管四个风塔站的下垫面条件存在一定的差异，但梯度风的风向风速表现出较为一致的季节变化特征，最大风速均出现在8月，这与副高脊线位置的北抬有关，而冬季和初春的较大风速与冷空气的活动和入海高压后部的偏南大风有一定的关系。

(2) 四个风塔站的指数律参数α也表现出一定的季节变化特征，这与气候的季节变化和下垫面热力特性引起的大气层结稳定度的变化密切相关。此外在风速较小的情况，由于大气层结较为稳定，α值相对较大，而当风速增大到一定程度以后，各层空气充分混合，α也趋向于一个与风速无关的稳定值。另外值得注意的是，9—12月大渔山和佛渡两个海岛站的α都为负值，这与海洋热力特性有关，当然由于这两个站的观测高度较高，因此该α值反映的应该是海面上较高层大气的稳定度状态。

(3) 海面风速反演的准确率与指数律参数α的选取密切相关。由于参数α存在一定的季节变化特征，因此有必要使用分月α值来反映这种变化。四个风塔站的风廓线率试验表明海岛风速反演受下垫面状况和大气层结状态的影响，而后者对于结果的影响更加明显。目前很难选取单一一种风廓线率用于风速反演，而需要分季节使用风廓线率，1—6月可以使用大渔山风廓线率，而7—12月可以使用佛渡风廓线率。使用混合风廓线率得到的ME为0.04 m·s^-1，MAE为1.51 m·s^-1。海面风场优化试验表明，可以通过计算统计误差量(MAE和RMSE)来筛除部分海岛中尺度站从而提高海面风场的反演质量，经过优化的海面反演风场的MAE和RMSE分别为1.28和1.68 m·s^-1。此外试验表明海岛中尺度站反演风场的有效影响范围至少可达30 km。基于上述方案可以获得高质量的海面格点化风场，从而为海面风场的精细化监测和预报提供技术支持。