引言

中小河流是指流域面积在200~2000 km²的河流，该类河流网络覆盖了我国85%的城镇和农村地区。区域复杂性和时空变化多样性使得对中小河流子流域的识别存在较大难度。此外，中小河流洪水破坏强度大、致灾时间短和爆发性强等特点使得中小河流暴雨致灾预警预报成为当前各国政府和防灾服务领域关注的重点, 其中，由短时强对流暴雨产生的中小河流灾害是近来气象灾害防御研究的方向，也是最近国内外研究的热点和难点。在国内，气象、水文等部门均开展了中小河流治理与洪涝灾害防御研究工作。研究中小河流暴雨致灾阈值是灾害管理的重要内容之一。暴雨致灾阈值研究的首要任务是对降水与径流的雨洪关系进行相关性分析，最终建立基于降水量的气象灾害预警机制。在水文模型的灾害预警研究领域，意大利proGEA公司基于TOPKAPI分布式水文模型和GIS技术开发了中小河流预警预报系统并得到推广和应用(刘志雨, 2005)；希腊Grillakis等(2010)利用HBV模型和降水雷达短时降水预报对斯洛文尼亚热莱兹尼基(Zelezniki)区域的中小河流进行洪水预报，得到了很好的预报结果, 美国国家气象服务水文管理中心采用Sacramento Soil Moisture Accounting (SAC-SMA)模型对全美4000个水文观测点进行逐日的水文预报，通过复杂的参数订正过程后取得较好效果(Smith et al, 2013)；美国军方工程集团水文工程中心基于地理信息完成了分布式水文模型-HEC_HMS(Hydrologic Engineering Center_hydologic modeling system)的构建受到国内水文领域学者的关注, 如林峰等(2009)利用该模型建立了福建省晋江西溪流域降雨径流模型并研究了不同时间尺度条件下模拟步长对模型运算的影响。基于地理信息技术的中小河流暴雨致灾研究在我国起步较晚，水利部水文局2010年开展了中小河流山洪监测与预报技术研究。该课题系统性地研究了湖南湘江支流洣水流域和江西赣江支流遂川江流域暴雨灾害防御，但研究重点在于中小河流站网监测、水文预测和风险预警等规划工作[水利部水文局(水利信息中心), 2010]，对降水与洪水致灾等相关课题的研究较少。气象部门也开展了相关研究，文明章等(2013)利用Floodarea水动力模型对给定流域进行淹没模拟，实现淹没过程再现，同时推算出给定点的临界雨量阈值，然而该方法涉及到高精度的高程数据，需要大量的计算资源，对中小河流流域阈值计算能力有限；当前，中小河流暴雨致灾研究由于资料匮乏、河道变化复杂及人工调蓄工程等因素的影响使得实用成果有限，业务应用与支撑系统更少。强降水是中小河流径流变化致灾的主要原因，然而，受土地类型、植被指数、河道糙率和水资源调蓄等多种因素的影响，降水与径流并非简单的线性关系，而是以一定非线性关系存在。此外，某一流域径流变化不仅受本流域面雨量变化的影响，而且受上游流域径流变化的影响。基于数字高程模型(digital elevation model, DEM)高程数据和D8算法，本文实现了与湖南水利观测站网一致的中小河流流域划分，形成了湖南中小河流流域集合，利用湖南“四水”流域洪水传播时序关系，构建了各中小河流子流域相互影响的有向拓扑图，描述了时空范围内各子流域间的相互关系并提出了中小河流流域等效面雨量的概念和计算算法; 利用40年逐日降水观测资料和等效面雨量计算算法得到了各子流域的等效面雨量序列，结合子流域水文控制站观测序列，实现了用于暴雨致灾阈值分析的隐马尔可夫模型(许博等, 2012)的构建。利用水文控制站相关参数和隐马尔可夫模型计算了中小河流洪水灾情发生前1~5 d的累计面雨量序列概率，从而实现了不同时间尺度条件下的各子流域暴雨致灾的临界雨量阈值的确定过程。

1 数据与方法

本文研究空间范围为湖南(25.0°~30.0°N、108.8°~114.3°E)主要降水汇流区域。研究对象为降水条件下湖南湘江、资江、沅江、澧水四大流域所属中小河流各子流域的暴雨致灾临界雨量确定问题。文中采用的水文观测资料为湖南省水利局整理的1965—1980年87个水文控制站汛期(4—9月)逐日的水文观测资料，降水数据为国家气象信息中心整理下发的1970—2000年逐日降水的历史整编资料。考虑到水文观测资料的完整性结合中国气象局“山洪暴雨风险普查工作实施方案”^①的相关要求，选用60个与中小河流子流域相配的水文站观测资料为研究数据。考虑中小河流降水汇流的空间影响，结合湖南洪水传播时间时序关系并基于本文提出的中小河流等效面雨量的概念和相应的计算算法，生成了与中小河流流域相匹配的从1965—1980年的逐日等效流域面雨量序列。

① 国家气候中心.2013.暴雨洪涝灾害致灾临界(面)雨量确定技术指南.

中小河流暴雨致灾临界雨量阈值确定方法是近些年来气象防灾减灾研究的新内容，基于模式和统计等多种方法不断地被得到完善和修正，在总结中国气象局山洪普查与阈值确定工作的基础上，本文将隐马尔可夫模型用于暴雨致灾雨量的确定工作，主要采用如下方法：(1) 基于D8算法利用GIS工具实现基于DEM高程数据的子流域划分；(2) 基于国家级观测站和国家基准站的逐日降水观测数据，使用Kriging插值方法构建流域面雨量数据集；(3) 有向图递归算法：利用洪水传播时间表，结合等效流域面雨量，构建流域洪水传播有向图，使用有向图递归算法计算中小河流各子流域等效面雨量；(4) 分类方法：为构建合理的隐马尔可夫模型状态集，本文针对不同特征的数据序列，采用不同的分类方法，对等效面雨量序列(离散性明显)，采用自适应K-均值分类方法，对水文观测序列(有一定连续性且变化区间较小)采用直方图分类法；(5) 期望值最大化算法(expectation maximization aldgorithm, EM)：利用降水资料和水文观测资料形成了隐马尔可夫模型的系统状态集合和观测状态集合以及状态转换概率矩阵，实现了隐马尔可夫模型的构建，基于水文观测状态序列和EM方法，求得达到灾害临界(或警戒水位)条件下，最大概率的降水状态序列最优参数估计值和相应的概率值。

2 湖南水文气候状况

湖南为大陆性热带季风湿润气候区域，年平均降水量为1403.1 mm，降水时空特征明显，每年4—9月为集中降水期，其中，从4月开始，湖南降水量经历两个时间剧增(4月第2至第4候、5月第1候至6月第5候)，最大候平均降水量为49 mm(吴贤云等, 2015)，段亚雯等(2014)利用1961—2010年逐日降水、气温观测资料，对中国典型区域进行了降水集中指数(PCI)研究, 证明了长江中下游PCI指数在12~17变化，降水集中在6—7月。根据湖南极端气候事件监测系统显示，湖南1 d极端降水最大值为455.5 mm，连续2 d最大降水量为541.4 mm，连续3 d最大降水量为619.7 mm，连续5 d最大降水量为623.1 mm, 强降水集中期、独特的地形地貌和复杂的中小河流特征导致湖南中小河流汛期暴雨灾害频发，灾情损失严重。仅2014年，因洪水灾害造成的社会损失占湖南自然灾害损失总量94.2%，暴雨灾害共导致53人死亡，直接受灾人口153.3万人^②。

② 湖南省民政厅.2014.2014年湖南省自然灾害年度报告.

另一方面，受能源需求的影响，湖南拥有水库14121座，总库容量为530.7亿m³，水电站4467座(装机容量为1534.8万kW)，总水利工程规模位居全国首位(湖南省水利厅等，2013)。系列的调蓄工程破坏了自然条件下的降水-径流关系，增加了基于水文模型的开展暴雨阈值研究的复杂性和暴雨致灾阈值确定的不确定性。

3 基本原理与理论

对某一研究流域，其日流域面雨量(R)可分布在k个不同的区间内，每个区间出现的概率为π_i[即P(R_{i|i=1, 2, …, k})=π_i]，在观测时间t内(t为出现暴雨灾害前连续降水日数)，该流域水文控制站观测观测序列为l_t, l_t-1, …, l₁、同步的降水序列为o_t, o_t-1, …, o₁，日降水量o_k条件下产生径流l_t的概率为b_{k, t}(b_{k, t}∈B)，降水量o_t转变成o_k的概率为α_{t, k}(α_{t, k}∈A)。则，对一给定的水文观测序列l_t, l_t-1, …, l₁，基于降水转换概率矩阵A，径流状态转换概率矩阵B和初始降水概率向量π的四元组条件λ下[令λ=(L, O, A, B, π)]，利用式(1) 得到有效面雨量序列o_t, o_t-1, …, o₁的概率。在给定的径流序列条件下，若存在多个o_t, o_t-1, …, o₁观测序列与其对应，那么取概率最大的序列为灾害发生条件下对应的雨量序列，该序列对应的降水累计值为灾害发生条件下的暴雨致灾面雨量阈值。

$ \begin{array}{l} \mathit{P}\left({\mathit{\boldsymbol{O}}/\mathit{\boldsymbol{\lambda }}} \right) = \sum \mathit{P}\left({\mathit{\boldsymbol{O}}, \mathit{\boldsymbol{L}}/\mathit{\boldsymbol{\lambda }}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum \mathit{\boldsymbol{\pi }}{_{{l_1}}}{b_{{l_1}}}\left({{o_1}} \right){a_{{l_1}{l_2}}}{b_{{l_2}}}\left({{o_2}} \right){a_{{l_2}{l_3}}} \ldots {a_{lt - 1}}{b_{lt}}\left({{o_t}} \right){\rm{ }} \end{array} $

(1)

满足：

$ \begin{array}{l} {a_t}\left(i \right) = p\left({{o_1}, {o_2}, \ldots, {o_t} = i|\mathit{\boldsymbol{\lambda }}} \right)且{a_1}\left(i \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P\left({{o_1} = i, {l_i}|\mathit{\boldsymbol{\lambda }}} \right) \end{array} $

式中，a_t(i)表示在概率模型λ条件下，观测值o_i在t时刻等于i的概率。

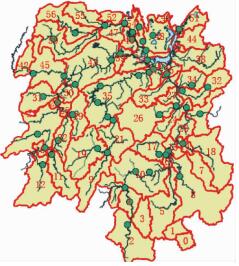
4 基于HMM模型临界雨量分析 4.1 基于DEM高程数据的中小河流流域划分

中小河流临界雨量阈值研究的本质是研究中小河流流域内降水形成的径流与本流域内面雨量的关系。因此，中小河流流域边界的确定和划分是研究降水阈值的基础。中小河流洪水来源于相关的山洪沟流域，流域划分应与降水汇流的物理过程一致同时也需要防止流域内因高程差异带来的边界不连续性(孤岛现象)情况。此外，受区域降水空间差异的影响、河道断面特征、河道长度、河沟坡降和流域地表持水率的不同，相同的降水量也会产生不同的径流量。此外，中小河流流域划分也需要兼顾水文观测站网的分布，尽可能保证每个流域内至少有一个水文观测站, 以确保每个研究流域有可靠的水文观测数据支持。本文以1 50000的DEM高程数据为数据源，根据湖南水文观测站分布情况，利用汇流模拟D8算法(赵健等，2006)和ArcGIS的hydro-logical tools工具对目标区域流域进行划分，得到全省中小河流流域子流域划分(图 1)所示。图 1中，红色多边形为基于DEM进行流域分割的结果，绿色圆点为基于研究流域内主要河流主干流域监测的水文控制站，可以看出本文流域划分结果与水文监测站网基本一致。

4.2 子流域面雨量的计算

为了得到合理的流域面雨量，采用地质统计分析法(刘爱利等，2012)对日降水量进行空间插值，形成流域面雨量序列。为得到适合湖南省降水条件下Kriging插值的最优参数，本文通过计算30年平均降水量的空间分布，得到各雨量站间的变异数；利用线性变差模型、指数变差模型、球面变差模型和高斯变差模型对平均雨量进行分析，并调节相应块金方差获得稳定性的最优值，得到的分析结果如表 1所示。

表 1为在不同插值模型条件下获得的相关参数。可以得知当Kriging模型选择指数模型时，块金值最低且模拟稳定性最好(偏基台值/基台值=0.834)。因此，利用与指数模型对应的最优块金值和偏基台值参数，本文对空间域站点日降水数据序列进行Kriging插值，得到子流域逐日面雨量序列。

4.3 基于流域面雨量构建等效流域网络

中小河流流域水情变化不仅受本流域内降水影响，同时受到上游流域来水的影响。因此，需要从时间-空间的二维空间上考虑降水对给定流域径流的影响。邓柯(2004)和叶泽纲等(2002)研究“湖南四水”内主要子流域在汛期期间的洪水传播过程(表 2)，该模型考虑了河道长度、河道比降、河道植被和河道糙率等地理条件下中小河流河道洪水传播的速度和子流域间的传播关系，是真实条件下降水汇流方向和汇流时间的经验模型。

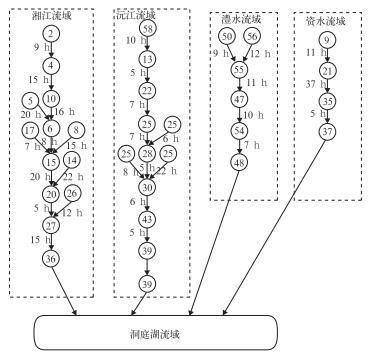
根据洪水传播表和中小河流流域划分的结果，构建各子流域之间的传播关系(洪水传播有向网络图)(图 2)，其中节点号代表流域号，权值为洪水自上游到下游的平均经历时间。此外，为研究空间域各子流域降水对径流影响，本文提出了等效流域和等效流域面雨量的概念。

定义1：等效流域(C_i):一个流域集合，该集合内任意流域的面雨量产生的径流在相同时间段U_i内可以通过固定参考节点;

令t_{i, j}为流域i的径流通过固定河道流经流域j所需时间，则：$ {\mathit{\boldsymbol{C}}_i} = \{ {t_k}|{t_{k, j}} < {\mathit{\boldsymbol{U}}_j}, \forall k, i \in D\} $

定义2：等效流域面雨量(R_i)：单位时间内等效流域C_i内的单位面积的降水量。

对一给定的中小河流流域，流域等效面雨量是本流域内径流产生的主要来源，为便于动态计算所有子流域等效面雨量，基于有向拓扑图，提出了求解中小河流各子流域的等效流域面雨量的递归算法(图 3)。

4.4 基于隐马尔可夫模型的等效流域临界雨量阈值确定 4.4.1 状态的分类

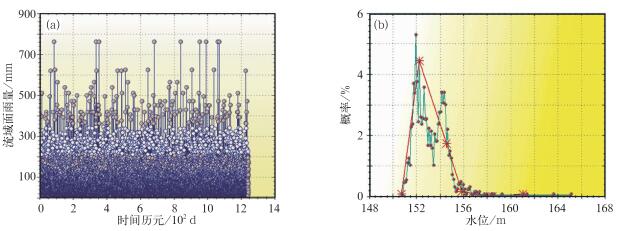
为构建合理的隐马尔可夫模型，需要对观测序列进行分类以构建系统状态集和观测状态集。受天气过程的影响，某一站点日降水序列在时间维上表现“聚集性”特征。Sivakumar等(2009)证明了日降水数据为混沌序列。然而相对于日降水序列，某一站点的径流数据序列和水位序列均有一定的连续性；因此，对降水序列和水位序列，本文采用了不同的分类方法。对降水序列采用K-均值分析法, 而对水位序列采用直方图统计分析法结合曲线拟合求拐点的分类方法(简称直方图分类法)(图 4)。图 4a为运用K-均值方法对某一雨量数据序列进行5个区间的分类，图 4b为基于直方图分析法对水位数据序列进行分析，并利用曲线拟合求拐点方法将该数据进行分类。

4.4.2 基于隐马尔可夫模型的临界雨量阈值确定

对每个中小河流子流域，利用历史观测资料和水文同步观测资料，构建隐马尔可夫模型的降水状态转换矩阵O，径流状态转换概率矩阵A和降水-径流转换矩阵B和径流初始状态向量π。对各水文控制站出现灾害前N天降水序列构建径流状态序列，选择概率最大的观测序列为预警条件下的径流序列，基于隐马尔可夫模型并利用EM算法求得在给定径流序列条件下对应的最大流域面雨量序列和相应的累计面雨量值。

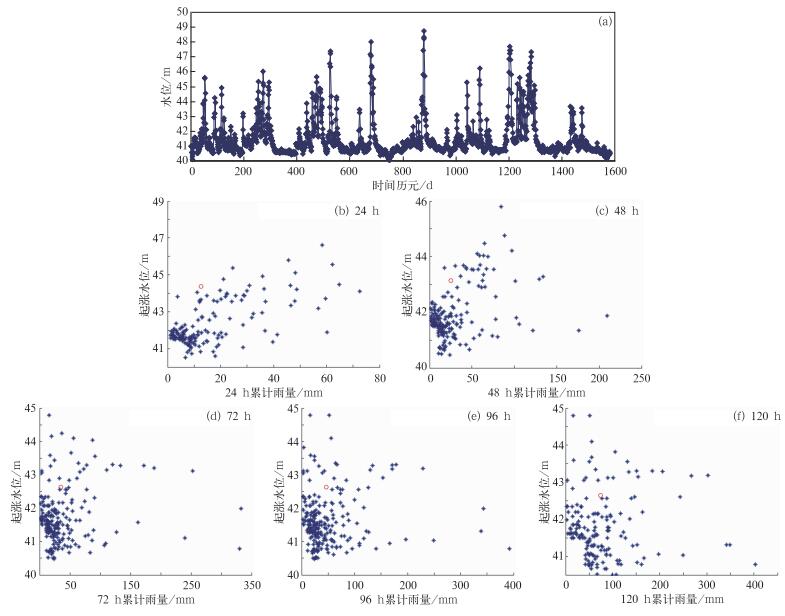
5 检验与应用

在实际应用过程中由于灾害预警直接与水位关联，且每个水文控制站均有降水-径流关系曲线图，为方便中小河流洪水预警业务运行同时降低阈值确定的中间变换过程，用水位替代径流，直接建立降水和水位的隐马尔可夫模型。本文采用的研究流域为图 1中第10号子区域，从图可知，流域2、4子流域为该流域的上游流域，基于有效流域划分方法，形成了以10号流域为下游的包含流域2和流域4的等效流域，流域面积为1.9876万km²，其中归阳水文观测站为等效流域的水文控制站。图 5为归阳水文站2004—2010年汛期(4—9月)的逐日流域面雨量数据序列和水位-降水关系图，其中图 5b~5f表示了在观测时间为24、48、72、96和120 h条件下，利用统计模型(章国材，2014)计算湘江(归阳站)由起涨水位至警戒水位条件下所需要的累计面雨量(圆圈所示)，相应的降水临界值如表 3所示。

利用K-均值分类方法(Kanungo et al, 2002)，将该等效流域面雨量数据序列划分成5个部分。利用直方图分析方法(Glasbey, 1993)，将水文观测水位序列划分成5个子区间，数据区间如表 4所示。

基于系统状态集和观测状态集形成HMM模型并利用EM方法得到1~5 d警戒水位条件下的最大概率降水序列和概率值，将各区间的有效值进行求和，得到该尺度条件下的临界面雨量阈值，计算结果如表 5所示。

数据结果显示两种方法对归阳站在不同观测时间尺度条件下计算的临界面雨量基本一致。另外，对图 1所示的子流域集合中选择5个子流域进行对比分析，并将计算结果列于表 6。

表 6的结果进一步证明本方法与统计方法基本一致。为验证本方法的有效性，以2010—2016年实际观测雨量数据为依据，对表 6涉及的流域临界雨量验证，验证所用雨量为相关流域出现警戒水文条件前24 h累计面雨量，并利用式(2) 计算两种方法的阈值与观测样本的几何距离，结果如表 7所示。

$ \mathit{R}{\rm{ = }}\frac{1}{\mathit{K}}\sqrt {\sum\limits_{\mathit{i} = 1}^\mathit{K} {{{\left({{\mathit{x}_\mathit{i}} - \theta } \right)}^2}} } $

(2)

式中，R为阈值与警戒水位对应的实际面雨量的平均误差，单位为mm；K为出现警戒水位的过程数；x_i为第i次出现警戒水位过程前的等效流域面雨量值；θ为对应的阈值。

经过实况资料和等效流域面雨量计算结果显示统计法和HMM方法的阈值几何距离平均值分别为：4.21和3.78 mm，对应方差为4.26和2.2。由此可见，相对于统计法，基于本文提出的方法有较好的准确率和更好的稳定性。

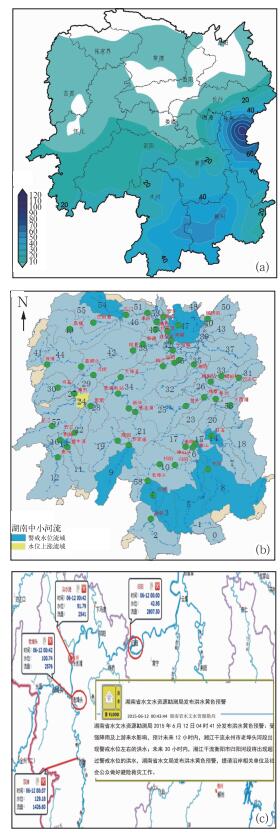
为验证阈值在气象防灾减灾中的业务应用情况，利用本文提出的方法，开发了相应的阈值分析平台和洪水预警分析平台，利用2015年6月12—13日的降水预报对湖南中小河流暴雨洪水开展预估。图 6a为湖南省6月12日08时至13日08时的降水预报图，图 6b为基于该降水预报结果的中小河流洪水预报结果，图 6c为湖南省水文局实况预警图。可以看出，基于本方法的阈值能成功预报出双牌、老埠头、归阳和衡山站的警戒水位。但也存在错报情况，如罗家庙、石门和南嘴站，经过检查发现，罗家庙所在流域(9号流域)错误主要是受降水预报误差的影响，其他则主要是该流域阈值计算偏低造成的，故需要根据业务运行效果对阈值进行检验和修订。

6 结论与讨论

基于DEM高程数据和湖南水文观测网络，构建了阈值研究的有效空间范围(中小河流子流域)，利用水文传播时序关系，构建了流域洪水传播有向图，结合子流域和加权有向图，提出了等效流域面雨量的概念，结合有效流域面雨量与同步水文观测数据，本文提出了基于隐马尔可夫模型的中小河流临界雨量阈值分析方法，并将该方法对实况灾情雨量比较，实验证明，相对传统统计法，新方法具有准确性高，误差空间小的特点；基于该阈值系统构建的阈值服务平台的实际业务运行也证明了新方法具有较好的业务支持能力，但在应对复杂天气过程的计算中也存在准确性不足的问题，需要在业务中进一步应用和验证。本阈值确定方法和预警系统具有如下特点：

(1) 不同于传统的基于站点的面雨量预报技术，本文提出了基于洪水流域时间响应和流域等效面雨量概念开展中小河流暴雨临界雨量阈值研究，在时间维和空间维对降水-径流进行研究，提高了临界雨量阈值确定的准确性和阈值空间的稳定性。因此，在阈值应用过程中，可以采用动态计算等效面雨量的方法和阈值进行比较开展中小河流实时预警服务，有较好的业务应用价值。

(2) 受水文观测站上游水坝等人工调蓄的影响，阈值统计法在阈值计算和预警服务过程中会受到干扰，需要大量的人工干预去识别有效起涨水位，相关统计参数选择的带主观性，难以满足业务的实时预警服务。基于HMM方法，采用了观测数据分类和相关状态转换概率的计算，一定程度上降低了随机干扰的影响，同时方便阈值分析自动化和预警业务化应用。

(3) 基于HMM方法进行的阈值确定效果受HMM模型结构的影响，尤其是观测数据的分类和状态集合的构建过程对隐马尔可夫模型的结果有一定的影响，状态分类对隐马尔可夫模型的影响也是当前智能计算领域研究的热点，也是未来研究的重要内容之一。

(4) 降水-径流的因果关系是本文研究的理论基础，然而受数据获取的完整性和洪水预警的现实需要，阈值确定用降水-水位的关系代替降水-径流的方法在一定程度上降低了阈值确定的准确性，因此阈值也需要在业务应用中不断得到修订和完善。

(5) 在阈值的洪水预警的应用过程中，洪水预报准确性受到降水量预报准确性的影响，同时也受水资源人工调蓄的影响。因此，阈值的修订与预报应该与水文观测实况资料相结合，也是本工作未来努力和研究的方向。