引言

极端天气事件对人类社会和环境有很大的影响(王绍武等，2003)，极端天气事件作为一种小概率天气事件，突发性强，造成的经济损失严重(杨金虎等，2008)，政府间气候变化专门委员会(IPCC)第三次报告(IPCC，2001)定义，对一特定事件和地点，极端天气事件就是发生概率极小的事件通常发生概率只占该类天气现象的10%或者更低。在极端天气中，对极端降水的预报和预警是气象及科研工作者的研究重点。

强降水的长期变化特征显示，极端降水事件显著增加(Karl et al，1998；Stone et al，1999)。王志福等(2009)研究表明，极端降水与年降水总量关系密切，其发生频数具有上升趋势。江淮流域梅汛期的极端降水量和极端降水站次自1980年以来呈上升趋势(杨玮等，2015; 江志红等，1999)，华北则呈减少趋势(翟盘茂等，2003)，而东北地区的极端降水的频次和强度有增加(杨素英等，2008)。在全球变暖的条件下，华南地区的冬季极端降水强度也有所增大(Zhi et al，2010)。刘学华等(2006)利用极端气候指数对我国年极端降水事件的变化趋势进行了分析，强降水日数和强度均有增大。刘琳等(2013)基于集合预报提出了极端降水指数，可提前3~7 d发出强降水信号。

由于模式的初值误差、模式误差和大气系统的混沌性，使得数值预报存在不确定性(Lorenz，1965；矫梅燕，2008)，因此由单一化的确定性预报向概率预报是必然的结果(杜钧等，2010；王东海等，2011)。集合预报系统会产生大量的预报结果，现已有很多集合预报解释应用的方法(陈静等，2002；毛恒青等，2001)，如集合平均图、集合预报离散度、面条图、概率烟羽图、各种聚类方法等。相较于确定性预报，从集合预报的结果中更加容易提取出极端降水的概率，把该概率作为先验概率，将贝叶斯理论应用于集合预报产品的解释中，是近年来集合预报应用的一个新趋势。

贝叶斯方法作为一个新的学派，很多学者已经应用贝叶斯方法对要素预报进行订正。智协飞等(2014)采用贝叶斯平均(BMA)方法对温度进行了多模式集成，其结果优于集合平均，且BMA预报融合了各成员对预报不确定性的描述，使之与观测值更为接近。刘建国等(2013)基于TIGGE多模式集合预报，对淮河流域的气温建立了BMA模型，结果表明BMA模型比原始集合预报效果好；单中心的BMA概率预报都有较好的预报效果。李爱华等(2012)基于贝叶斯最大熵方法研究了甘肃省多年平均降水的空间化，可以更好地体现研究区域的降水空间分布情况。陈朝平等(2010)基于西南区域中心的中尺度区域集合预报系统的48 h预报，根据贝叶斯公式求得暴雨后验概率分布，建立暴雨预警模型。

Roman等(2006a; 2006b)在2004年提出了针对二分类预报量即判断降水是否发生的贝叶斯产品处理技术(Bayesian Processor of Output，BPO)理论框架。2006年完善了二分类型预报量的BPO理论，并做检验。陈法敬(2011)选取长沙和武汉站地面气温作为预报量，利用BPO方法，建立集合预报成员的似然模型，并将单一集合成员预报转化为概率预报，得到预报能力高于单个成员的集成贝叶斯概率预报。韩焱红等(2013)、张宇彤等(2013)选取了广州、武汉、成都、南京站的降水量作为预报量，TIGGE集合资料的降水资料作为预报因子，对基于贝叶斯理论的BPO方法进行初步应用试验。在BPO的模型中，Roman等(2006a；2006b)给出了计算二分类变量的后验概率。本文将选取T213集合预报成员作为预报因子，把贝叶斯理论应用于极端降水预报中，进行极端降水概率预报试验，以提高极端降水事件的预报能力。

1 极端降水预报的贝叶斯方法 1.1 极端降水的贝叶斯统计方法

贝叶斯公式是贝叶斯理论的核心，由预报量Y和预报因子X的贝叶斯公式如式(1) 所示：

$ P\left({X|Y} \right) = \frac{{P\left(X \right)P\left({Y|X} \right)}}{{P\left(Y \right)}} $

(1)

式中，P(X)是未知数X的先验概率；P(Y|X)为联合密度函数或似然函数。P(Y)则为随机变量Y的边缘分布。公式表达了通过抽取样本Y，利用抽样信息对未知数X的先验概率进行修订，得到条件概率即后验概率P(X|Y)。

本文采用BPO原理(Roman et al，2006a; 2006b)中，降水后验概率的公式得到极端降水的概率，如式(2) 所示。其中，g为极端降水发生的先验概率，f₀和f₁分别为极端降水不发生和发生时条件概率密度函数(公式推导过程略)。

$ \pi = {\left[ {1 + \frac{{1 - g}}{g}\frac{{{f_0}\left(x \right)}}{{{f_1}\left(x \right)}}} \right]^{ - 1}} $

(2)

1.2 极端降水的阈值

本文将选取中国区域内的格点，利用贝叶斯原理通过式(2) 给出极端降水发生的概率。由对极端强降水事件的定义方法——百分位法，定义观测气候序列第95个百分位的降水为观测极端强降水阈值T。在全国区域内的每个格点上，将模式气候降水与观测降水的拟合分布进行比较，分别得到模式和观测的降水概率密度曲线f_c和g_m，由极端降水的阈值T可得到观测降水的PDF阈值，再将该PDF阈值映射到模式气候降水分布上，即当x₁=T时，令f_c(T)=g_m(T_m)，式(3) 中的T_m即模式预报的极端强降水阈值，当模式预报降水量≥T_m时，预报极端强降水发生。

$ {T_m} = g_m^{ - 1}\left[ {{f_c}\left(T \right)} \right] $

(3)

2 模式极端降水的定义及特征 2.1 观测极端降水的选取

本文选取了2008—2010年T213模式的集合预报历史资料，为了获得模式的极端降水值，首先需要分析与之相对应的观测极端降水分布特征，所以在本研究中，选取与模式资料降水时段相对应的观测降水时段，即2008—2010年6—8月的降水观测资料，作为观测极端降水定义的资料来源。

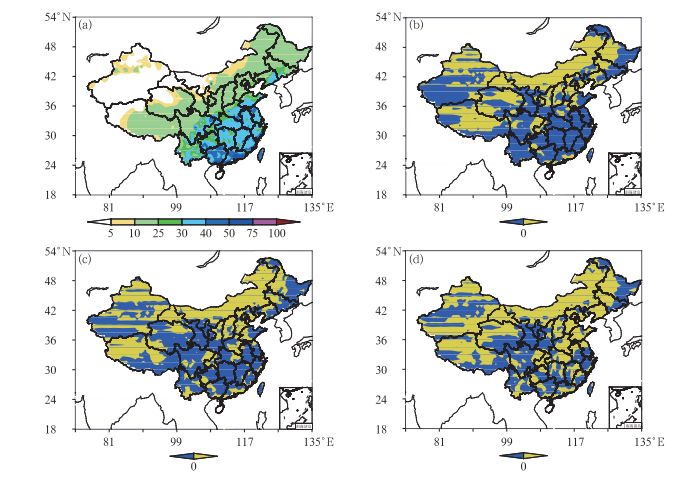
采用Cressman插值方法，将全国2412个观测站点插值到T213的模式网格点上，对各格点的观测降水量进行分析。观测极端降水的定义采用翟盘茂等(2003)提出的百分位法来定义观测极端降水，将全国区域内每个格点的观测日降水量(n=276) 按照升序排列，定义第95个百分位上降水量的3年平均为该格点的极端强降水阈值T。当某日降水量超过该格点的极端强降水阈值时，则称该格点出现极端强降水，否则无极端强降水发生。图 3a为我国观测的极端降水分布图，由图可知，极端降水的分布情况与我国雨带分布情况类似，自西北至东南降水量呈递增趋势。

2.2 观测降水和模式降水概率分布函数

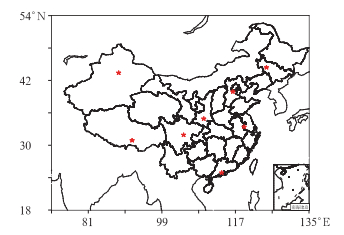
根据陈隆勋等(1991)对中国降水气候区域的划分方法，将中国划分为8个气候区域，图 1中的五角星为不同气候区域的代表格点分布图，表 1为代表格点的经纬度。由于夏季降水量的分布为偏态分布，本文采用Gamma分布(Roman et al，2006a; 2006b)，对8个代表格点进行拟合，其概率密度函数的显著性水平检验为0.05。在下文中，观测极端降水和模式极端降水的分布均采用Gamma分布函数对其进行拟合。

2.3 模式极端降水的定义

为了得到更准确的先验概率，运用1.2节中模式极端降水阈值的计算方法对模式降水的拟合曲线进行修订，对于中国区域内的格点，首先分别将观测降水资料和T213集合预报降水资料进行Gamma拟合，分别得到模式和观测的降水概率密度曲线，由观测极端降水的阈值T可得到观测降水的PDF阈值，再将该PDF阈值映射到模式气候降水分布上，此时模式极端降水的PDF值所对应的降水量即为模式极端降水阈值，该值即为本文对模式极端降水的定义。

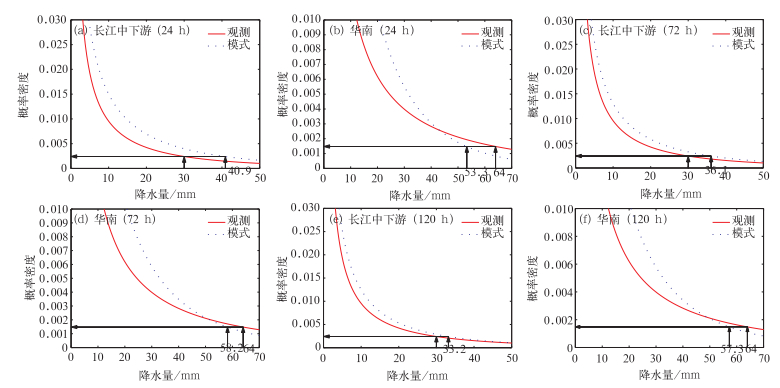
模式极端降水较观测极端降水来说，有变大和变小两种可能。以长江中下游(模式极端降水变大)和华南(模式极端降水变小)的代表格点为例，图 2给出了24、72和120 h预报时效的模式极端降水阈值计算图示。对于长江中下游的格点(图 2a、2c、2e)，模式降水的概率密度曲线位于观测降水的概率密度曲线之上，即模式对于极端降水的预报偏强。观测极端降水为30 mm，24、72和120 h预报时效修订后的模式极端降水为40.9、36.1和33.2 mm，模式较观测极端降水阈值变大，且随着预报时效的延长模式对极端降水的预报能力逐渐减弱。对于华南格点(图 2b、2d、2f)，模式降水的概率密度曲线与观测降水的概率密度曲线有交点，观测极端降水为64 mm，位于交点的右侧，24、48和120 h预报时效经过修订后的模式极端降水分别为53.3、58.2和57.3 mm，模式较观测极端降水阈值变小，说明修订后的模式极端降水阈值对于极端降水的预报偏弱，随着预报时效的延长，模式的预报能力变化不明显。中国区域其他格点的变化情况将在下文中给出。

对所选格点均进行上文中的修订，则可得到我国模式极端降水分布，由图 3给出。修订后的模式降水与观测降水的分布大体类似(图略)，也呈自西北向东南极端降水阈值递增的分布形式，图 3b、3c和3d分别给出了24、72和120 h预报的观测与模式极端降水的差值分布，以分析修订后模式较观测极端降水的变化。图 3b中，观测极端降水阈值大于模式的极端降水的地区，主要集中西北、内蒙古、华北、东北大部分地区，四川东部，广东和广西沿海，在这些地区，说明模式对于极端降水的预报偏弱；观测极端降水小于模式极端降水的地区，主要分布在东北东部、江淮流域和华南北部，模式对这些地区的极端降水预报偏强。随着预报时效的延长，山东、河南和西南地区的黄色区域明显变大，模式对极端降水的预报能力减弱的区域增多，当预报时效为120 h时，绝大多数地区，模式对极端降水的预报明显偏弱。

3 极端降水预报的模拟试验及检验 3.1 极端降水的先验概率和似然函数

本文将从集合预报的结果中获得极端降水的先验概率，对于区域内的一个格点，将某日集合预报成员的降水量分别与该格点的观测(模式)极端降水进行比较，大于等于观测(模式)极端降水成员占成员总数的百分比即为先验概率。计算公式如下：

$ \begin{array}{*{20}{c}} {P = (\sum\limits_i^N {{P_i}})/N}&{\begin{array}{*{20}{c}} {{P_i} = 1\;\;\;\;R \ge {T_m}}\\ {{P_i} = 0\;\;\;\;R < {T_m}} \end{array}} \end{array} $

(4)

式中，P为极端降水的先验概率，N表示集合成员数，这里N=15，P_i表示集合成员24 h累积降水量与实况极端降水的比较，R表示每个集合成员的24 h累积降水量，T_m表示每个格点对应的观测(模式)极端降水量。

在式(2) 中，(f₀，f₁)分别是当极端降水不发生和发生时，预报因子x(本章节取为集合平均)的概率密度函数，为似然函数族，根据2.2节中统计结果，采用Gamma分布函数来对预报因子的似然函数进行拟合，Gamma概率密度函数由式(5) 确定，Γ(α)通过欧拉第二类积分定义，其中α为形状参数，b为尺度参数。以西南格点(30.38°N、103.50°E)为例，z为西南格点的24 h集合平均，则似然函数族分别由式(6) 和式(7) 给出，当集合平均值z确定时，似然函数即可确定，在先验概率确定时，则得到后验概率。

$ f\left({z|a, b} \right) = \frac{1}{{{b^a}\Gamma \left(a \right)}}{z^{a - 1}}{e^{ - \frac{z}{b}}}, \;\;\Gamma \left(a \right) = \int\limits_0^\infty {{e^{ - t}}{t^{a - 1}}{\rm{d}}t} $

(5)

$ \begin{array}{l} {f_1}\left({z|0.5017, 4.0580} \right) = \\ \;\;\;\;\;\;\;\;\frac{1}{{{{4.058}^{0.5017}}\Gamma \left({0.5017} \right)}}{z^{0.5017 - 1}}{{\rm{e}}^{ - \frac{z}{{4.058}}}} \end{array} $

(6)

$ \begin{array}{l} {f_0}\left({z|0.7928, 11.0116} \right) = \\ \;\;\;\;\;\;\;\frac{1}{{{{11.0116}^{0.7928}}\Gamma \left({0.7928} \right)}}{z^{0.7928 - 1}}{{\rm{e}}^{ - \frac{z}{{11.0116}}}} \end{array} $

(7)

3.2 极端降水的后验概率

上文中，已获得先验概率和似然函数的计算方法，运用式(2) 即可求得每个格点的后验概率。根据极端降水阈值选择的不同方式，设计两种试验方案，分别简称为Pc方案和Pm方案。Pc方案选择观测极端降水作为先验概率的阈值，Pm方案选择模式极端降水作为先验概率的阈值。通过得到不同方案下先验概率，对比不同方案下的先验概率与后验概率分布情况，来选取更合理的方案进行个例分析。

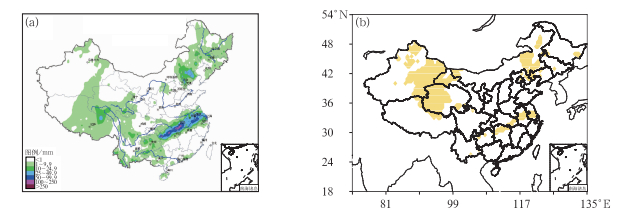
2010年7月12日，在江淮流域有一次明显的强降水过程，图 4为降水实况及极端降水分布情况。从图 4a中可知，降水地区主要集中在江淮流域，湖北东南部及湖南北部有两个降水量在100~250 mm的大值中心，并且，根据中央气象台的实况降水图，该降水过程从7月9—15日一直维持在江淮流域，这种持续性的强降水事件对人们日常的生产生活也有非常大的影响。图 4b中为极端降水的分布情况。

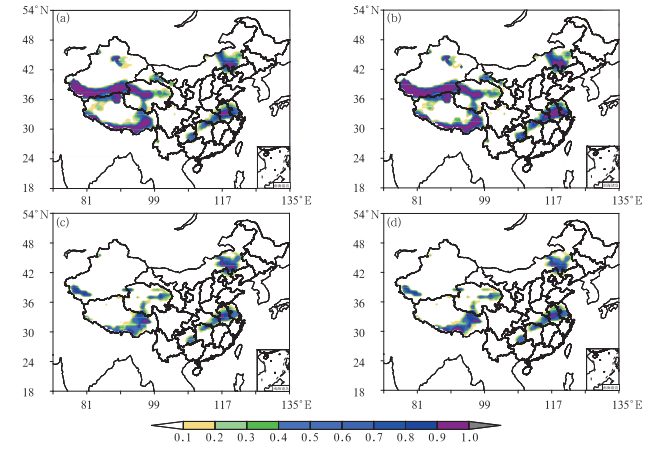
利用式(4)，分别计算Pc方案和Pm方案下24 h预报的先验概率分布，图 5为24 h预报时效的两种方案下先验和后验概率预报结果。首先对比Pc方案和Pm方案的分布差异，Pc方案中，先验与后验概率的降水预报在甘肃、高原南部和新疆南部有大面积的降水空报情况，主要降水雨带(江淮流域)的概率预报也较Pm方案偏强。而Pm方案的空报较Pc方案少，且对主要雨带也起到了明显的预警作用。然后对比先验与后验概率的分布，由于后验概率是在先验概率的基础上修订的，所以其分布形式与先验概率基本类似，只是强度不同。两种方案中，后验概率的预报明显偏强。总的来说，Pc方案中的空报明显过多，而Pm方案对于雨带也有较准确的预报，因此，在下文的个例分析中采用Pm方案对2012年7月21日的极端降水进行分析。

3.3 极端降水模拟预报检验

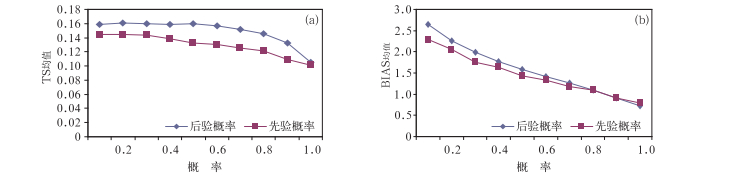
本文采取TS评分和BIAS，以Pm方案24 h预报时效的预报结果为例，对2008—2010年夏季的全国模拟概率预报结果进行检验，由于该预报结果为概率预报结果，因此分别计算先验和后验概率≥10%，≥20%，…，≥90%，=100%的TS和BIAS的全国区域平均值，图 6给出了24 h预报的模拟预报检验结果。对于TS评分，TS值越大，说明预报准确性越高，从图 6a中可以看到，后验概率的折线位于先验概率的之上，后验概率的TS评分大于先验概率的，当极端降水概率预报值≥20%时，后验概率的TS评分最高，达0.1608，随着概率的增大，TS评分逐渐减小，当极端降水发生概率为100%时，TS评分最低；对于BIAS来说，BIAS的值越接近于1说明预报偏差越小，由图 6b可见，后验概率的BIAS值整体偏大，这主要是修订结果的空报率较大，对于预报极端降水发生概率比较小的区域，存在一些虚假的警示。因此，经过贝叶斯方法修订后的极端降水预报，提高了极端降水产生的正确率，但空报有所增加。

4 北京“7.21”特大暴雨概率预报试验及检验

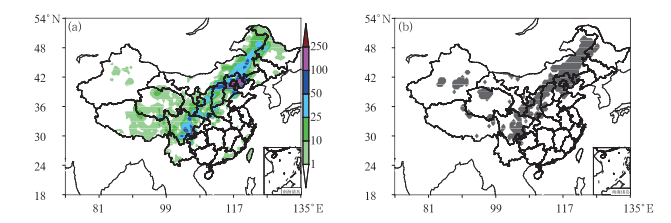
2012年7月21日，北京和华北部分地区遭遇百年一遇的特大暴雨，城市交通瘫痪、引发房山地区山洪暴发、严重影响了居民的正常生活。这次暴雨灾害，北京全市平均降水量达190 mm，房山区的降水量达460 mm，造成北京市的经济损失近百亿元，79人遇难，190万人受灾。事实上，不仅仅在北京，天津、河北等地当天也有一次大暴雨过程(周宁芳，2012；谌芸等，2012；俞小鼎，2012)。图 7a为24 h累积降水实况分布，北京、天津及河北北部降水量＞100 mm，在北京南部与河北省交界处，有一＞250 mm的大暴雨中心。整个极端降水雨带自东北向西南分布，为内蒙古东北部和华北、山西、陕西大部分地区和四川省中部地区。

4.1 2012年7月21日极端降水概率预报试验

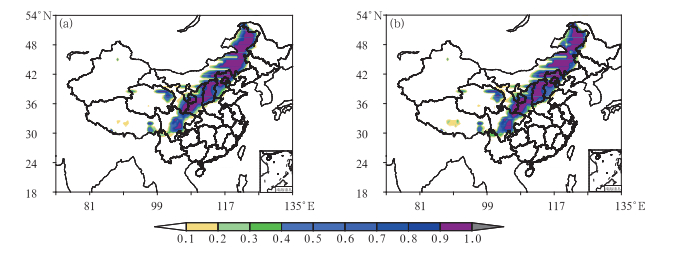
由上文可知，Pm方案的极端降水概率预报结果更为合理，因此在个例分析中采用Pm方案进行讨论。首先，运用式(4)，通过T213集合预报的降水结果确定“7.21”降水事件的先验概率g，再利用式(2) 计算降水后验概率π，即分别获得中国区域内的先验概率(图 8a)和后验概率分布图(图 8b)。对比先验概率(图 8a)和观测极端降水分布(图 7b)可知，先验概率对极端降水雨带位置的预报基本与观测相符，集中在东北西北部、华北地区、河套一带和四川中部，在山西南部空报较严重。对比先验概率(图 8a)和后验概率(图 8b)的极端降水分布，后验概率的预报较先验概率略偏强但不明显，在北京、天津和河北附近并无太大差异，主要在四川中部后验概率更大。

24 h预报的后验概率较先验概率的改进效果并不明显，由式(2) 可知，当先验概率为0时，后验概率也为0；而先验概率为1时，后验概率也为1。因此，当极端降水的先验概率值非常偏向这两个极端时，后验概率的变化并不明显。而集合预报对此次过程的24 h预报比较准确，先验与后验概率分布差异不大。下面对于72 h预报时效的结果再进行分析。图 9为72 h预报时效的先验和后验概率分布图。首先对比先验概率预报(图 9a)和观测极端降水分布(图 7b)，先验概率预报的雨带位置与观测略有偏差，概率大于90%的中心偏向实际雨带的北部，西北和高原有部分空报，这主要是集合预报系统的预报结果决定的。再比较先验概率预报(图 9a)和后验概率预报(图 9b)结果，后验概率较先验概率明显变大，在四川中部、甘肃东部和内蒙古东北部的极端降水信号明显增强，山西南部的空报仍然存在。

综合极端降水预报的检验结果和7月21日事件的72 h的预报可以看出，采用贝叶斯方法修订后的极端降水预报，提高了极端降水预报的准确率，但在一定程度上也增加了空报。

4.2 试验结果的检验

运用降水的TS评分和BIAS评分，对2012年7月21日的降水概率预报结果进行检验。表 2与表 3为24 h预报时效的检验结果，分别为先验和后验概率≥10%，≥20%，…，≥90%，=100%的TS和BIAS的全国区域平均值。首先看TS评分，后验较先验概率来说，除≥50%，≥60%和≥80%的TS小于先验概率的，在其他概率值上均优于或等于先验概率的，当极端降水发生概率≥70%时，后验概率的TS评分最大，为0.348；而对于先验概率来说，当极端降水发生概率≥80%时，先验概率的TS评分最大，也为0.348。然后看BIAS，该值越接近于1说明预报偏差越小，当极端降水的概率≥50%时，后验概率的BIAS更接近于1，整体来看，后验概率的BIAS较先验概率偏大。

因此，贝叶斯的极端降水概率预报较先验概率略有改进，但预报结果的空报有所增加。而上文中对模式极端降水阈值的修订，已经在一定程度上达到了对先验概率的改进，后验概率则能从更准确的先验概率中获得更合理的概率预报结果。

5 结论与讨论

本文采用贝叶斯理论研究了极端降水的概率预报方法，对观测极端降水和模式极端降水进行定义，并分别选取两者作为极端降水阈值，获得观测(模式)极端降水的先验概率。根据极端降水阈值的两种取法(观测极端降水和模式极端降水)，设计了Pc方案和Pm方案，进行了两种贝叶斯极端降水模拟概率预报试验，并讨论了Pc方案和Pm方案下先验和后验概率的分布情况，对24 h预报时效的极端降水模拟预报进行检验；最后采取Pm方案对2012年7月21日北京的特大暴雨个例进行了贝叶斯极端降水试验和检验，得到以下结论：

(1) 观测极端降水的分布情况与我国雨带分布情况类似，为自西北向东南逐渐递增的趋势。而采用Gamma分布对所有格点的观测和模式降水量进行拟合，根据观测极端降水阈值T得到模式极端降水阈值的分布情况，在西北、内蒙古、华北、东北大部分地区，四川东部，广东和广西沿海，模式对于极端降水的预报偏弱；在东北东部、江淮流域和华南北部，模式对这些地区的极端降水预报偏强。随着预报时效的延长，模式对极端降水的预报能力减弱。

(2) 以2010年7月12日江淮流域的降水过程为例，对比Pc方案和Pm方案的预报结果。Pc方案中，先验概率与后验概率的降水预报在甘肃、高原南部和新疆南部有大面积的降水空报情况，主要降水雨带的概率预报也较Pm方案偏强。而Pm方案的空报较Pc方案少，且对主要雨带也起到了明显的预警作用。两种方案中，后验概率较先验概率预报值更大。经贝叶斯方法修订后的极端降水预报，提高了极端降水发生的准确率，但空报有所增加。

(3) “7.21”北京特大暴雨事件中，24 h的先验概率和后验概率预报对雨带位置预报基本准确，后验概率较先验概率略偏强但不明显；72 h预报的有两个预报特征，一是雨带位置偏北，二是在四川中部，后验概率值明显较先验概率明显偏大。因此，贝叶斯的极端降水概率预报较先验概率有改进，但在一定程度上增加了空报。

总的来说，经过修订后的模式极端降水，先验概率和后验概率对于极端降水的概率预报效果均较好，都能够预报出雨带的大体位置，后验概率较先验概率的预警信号更强。贝叶斯极端降水的概率预报的结果仍依赖于集合预报系统的预报效果，集合预报系统的预报结果越准确，贝叶斯极端降水的概率预报效果也越好。