2. 江苏省气象台,南京 210008
2. Jiangsu Meteorological Observatory, Nanjing 210008
强对流天气常伴有雷电、冰雹、雷雨大风和短时强降水等灾害天气,做好对流性天气的预报预防对防灾减灾具有十分重要的意义。强对流天气具有尺度小、演变快的特点,目前对其预报难度大,传统的检验方法因空间一致性的要求,往往对强对流天气预报的检验评价较低,如采用常规的检验方法(如TS/CSI)需要预报与实况在格点或站点上严格的“一一对应”,当预报的目标出现一定的偏差时,TS评分可能很低,但即使TS评分很低的预报,也可能包含有用户(如预报员)所需的有价值的信息,如位置预报偏差较大却能够较好地刻画对流系统结构特征的预报。常规检验方法仅给出预报准确与否或者准确程度的评价,而不能给出预报存在偏差的原因,对一些区域目标仅给出简单的对错评价,而掩盖了预报中的一些积极的信息。同时,若要完善和改进预报产品,还需要通过预报检验获取预报偏差产生的原因,预报的检验也需要针对强对流天气的特征或用户的需要来设计(戴建华等,2013;邵晨等,2013)。因此,在强对流预报检验中引入能够挖掘预报潜在价值、适应不同用户使用倾向的非常规检验方法非常必要。
为了解决对高时空分辨率天气预报的检验,近年来开始采用一些新型检验技术,主要有两类(Ebert,2008),一类是基于对象的,主要是通过对降水系统进行识别,进而将预报和实况的目标属性进行比较(Davis et al,2006;尤凤春等,2011;刘凑华等,2013;符娇兰等,2014);另一类就是模糊检验方法(Ebert,2008),主要是通过将预报和(或)实况在不同的空间尺度、时间尺度、强度尺度或者其他重要的属性方面进行模糊化处理,并不需要预报和实况在各种尺度上的严格对应。
最初,模糊检验方法主要应用在中尺度数值预报模式的检验上。中尺度模式具有高分辨率的特点,有能力预报一些中尺度的对流天气系统,但是其预报的位置、强度或者时间可能与实况并不完全一致。而且由于对于某一个格点“预报发生而实况未发生”或者“预报未发生而实况发生”的双重惩罚原则,高分辨率模式的常规检验结果甚至没有低分辨率模式好(Mass et al, 2002)。鉴于传统的常规检验方法不能很好地评价高分辨率数值模式,国外不少学者基于各自不同的评价标准,通过降低预报与实况匹配要求的方法,在传统检验方法的基础上引进了新的预报检验方法,这一类方法被统称为“模糊检验方法”。以空间模糊为例,该方法在逐个格点上进行空间尺度放大处理,在放大后的尺度上通过计算平均值,取最小比例、计算概率分布函数等方法进行格点数据处理,再计算传统的误差和分级评分,这样相当于降低了预报和实况匹配的要求。通过空间模糊检验,用户可以得到预报产品在不同尺度上的信息,从而确定在何种空间尺度上预报是有用的,并根据自己的需求和应用倾向对不同的预报提供者进行取舍。总之,基于不同的用户对预报产品的准确度需求以及敏感性上是有差异的,模糊检验方法可以给用户提供不同尺度上的检验信息,从而让用户更好地应用预报产品。
强对流天气预报,特别是以雷达为基础的临近预报产品具有高时空分辨率的特征,引入模糊检验方法来检验强对流天气临近预报,可以充分发挥其优势来提供更客观和准确的评价,帮助提高强对流天气短临预报技术的完善和产品应用的水平。强对流天气的类型多,不同类型的强对流天气具有不同的特点,预报难度也存在较大差异,预报检验方法对各类天气的检验结果也会受到预报检验对象特征的影响。对比不同类型强对流天气预报在模糊检验中的差异将有助于对检验结果的正确评价。因此,本文选择了在形态、分布、尺度上各具特点的雷暴单体、飑线、大范围系统性强降水等三种典型的强对流天气,用空间模糊方法对中国气象局强天气短时临近预报系统(SWAN)和上海市气象局短临预报系统NoCAWS的1 h雷达回波外推预报产品进行检验和对比,并通过构造三种典型的强对流天气模型进一步研究各种模糊检验方法在不同情形下的适用性,以揭示空间模糊检验法在强对流天气预报检验中的潜在价值。
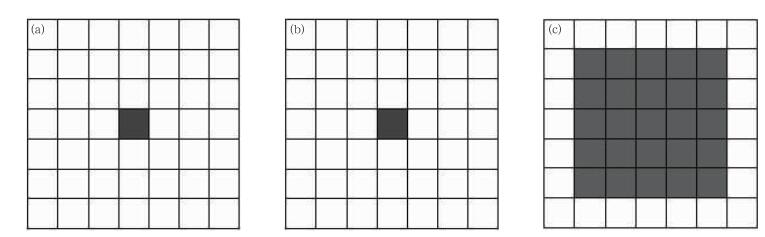
1 模糊检验方法介绍根据用户对预报的价值的取舍,即预报在何种程度上对用户是有意义的,模糊检验方法放松了检验标准(Ebert,2008),如图 1所示,对于空间上的格点预报,不再像传统检验方法中要求观测与预报格点一一匹配,而是认为只要预报与观测在空间尺度、时间尺度或者强度等属性上大致接近,就可以认定预报正确。以空间尺度模糊化为例,它的核心思想是在预报格点和观测格点周围选取一个尺度可变的窗区,如图 1c中的阴影部分所示,选择的窗区尺度由用户对一个有用预报的判定标准而决定,先对窗区内的数值采取平均、取阈值、计算概率分布函数等方法进行处理,然后再利用传统检验方法对处理后的数据进行检验,如计算TS评分、命中率、虚警率、均方根误差等。经过空间尺度模糊之后,用户可以通过自身的需求选择合适的评价策略,如对于城市预警的检验来说,只要强对流天气的落区在行政区域内,即可以判定预报准确,而不要其位置的严格一致,因此可以在较大的空间尺度上对预报水平进行评定,从而避免简单错误的评定。
|
图 1 传统检验方法与模糊检验方法对同一事件空间尺度模糊处理示意图 (a)观测, (b)传统检验方法, (c)空间尺度模糊方法 Fig. 1 The fuzzy treatment of spatial scale with the same event by traditional and fuzzy verification methods (a) observation, (b) traditional verification, (c) spatial scale fuzzy verification |
为了系统地介绍模糊检验方法,首先对本文中用到的符号进行说明。用X来表示单一格点内的观测值,用Y来表示同一格点内的预报值;〈〉s表示代表关注格点周围选定的窗区的值,s表示时空尺度;上标(-)代表平均值。
为了评价降水等预报的准确性,常采取一定的阈值来作为判断标准。采用I来作为判断因子(1=是,0=否),当降水量超过设定的阈值时,I值赋值为1,否则赋值为0。用Ix表示观测值的判断因子,用Iy表示预测值的判断因子。〈Ix〉s和〈Iy〉s分别表示模糊处理后窗区内的观测判断因子和预报判断因子,与Ix和Iy所不同的是,根据所选的方法不同,〈Ix〉s和〈Iy〉s也可能是0到1之间的任意离散值。〈Px〉s和〈Py〉s分别表示超过阈值的格点数占所在窗区内的总格点数的比例。
1.1 升尺度法升尺度法是模糊检验方法中最早的一种,也是最简单的一种(Yates et al,2006;Zepeda et al,2000;Weygandt et al,2004)。它先在大尺度(窗区)上分别对预报场和观测场取平均,然后再用传统的连续检验方法和分级检验方法进行检验。当需要评价一个模式预报的平均值是否可靠时可以采取这种方法,例如评估模式的面雨量预报结果。
| ${{\left\langle {{I}_{x}} \right\rangle }_{s}}=\left\{ \begin{matrix} 0&{{\left\langle {\bar{Y}} \right\rangle }_{s}}<阈值 \\ 1&{{\left\langle {\bar{Y}} \right\rangle }_{s}}\ge 阈值 \\ \end{matrix} \right.$ | (1) |
最小比例法(Damrath,2004)的初衷是基于实况和预报在一定范围内都不可能是百分百准确的假设,因此对于某一关注事件有可能在窗区内任意格点以相同的概率〈Px〉s和〈Py〉s发生。在窗区内,选取一个百分比阈值作为最小临界值,只要预报场中达到某一降水量级的格点数占窗区总格点数的百分比超过临界值,就判定预报事件发生。因此,对于最小比例法,某一事件的判断因子可以写成如下格式
| ${{\left\langle I \right\rangle }_{s}}=\left\{ \begin{matrix} 0&{{\left\langle P \right\rangle }_{s}}<{{P}_{e}} \\ 1&{{\left\langle P \right\rangle }_{s}}\ge {{P}_{e}} \\ \end{matrix} \right.$ | (2) |
式中Pe为最小临界值。因此最低要求的临界值应该是在窗区内至少有一个格点达到阈值(用anywhere表示)。根据不同的情况,检验者可以根据需要选择不同的临界值如30%或者50%等。根据不同的覆盖比例临界值,确定〈I〉s后,再计算传统的分级检验评分,如POD、FAR和ETS等。
1.3 模糊逻辑法在基于格点的传统检验方法中,是以观测数据准确为前提来进行检验的,如果预报结果与观测结果不一致,就判定预报为错。但是观测也不能保证百分之百的准确,如果观测有误的话,那么判断为错的预报值就有可能是对的。基于该假设,传统判断标准中的“击中”实际上也有可能是错误的,如果观测不是百分之百准确的,那么它有可能是一个“虚警”。事实上,观测和预报均具有不确定性。因此对于某一事件是否发生的判断不再是传统的0, 1二元论,而是用一定的发生概率表示(Damrath,2004)。
| ${{\left\langle I \right\rangle }_{s}}={{\left\langle P \right\rangle }_{s}}$ | (3) |
基于模糊逻辑的理论,Ebert(2002)通过在放大后的窗区内计算概率分布函数的方法对传统的0,1二分类列联表进行概率化处理,并实现了二分类列联表的归一化(表 1),再计算传统的检验评分。其中〈Px〉s和〈Py〉s即观测和预报分别超过某一阈值的概率。本文所涉及的模糊逻辑方法仅计算了空间分布上的概率分布函数。
|
|
表 1 模糊逻辑处理后的二分类列联表 Table 1 The contingency table of fuzzy logic method |
在之前的检验方法中,只考虑了一种因子作为预报准确与否的判据,且观测和预报是做了相同的尺度模糊处理。在多事件列联表(Atger,2001)方法中,对于某一个事件,考虑了几个不同的因子作为预报准确与否的判别标准。如对于强度列联表,分别采用几个不同强度阈值作为预报准确的判别标准,再计算传统的评分方法;对于空间列联表,分别采用几个不同的空间搜索尺度(窗区),只要预报的事件在该搜索尺度内发生即判定预报准确。本文所涉及的多事件列联表采用空间列联表的方法。
得到多事件列联表之后,可以针对不同的判别标准,计算命中率(POD)和虚警率(F),并利用这两个评分绘制ROC图。与ROC对应的,也可以计算HK评分。与前文所述的方法略有不同的是,多事件列联表只对预报进行了尺度模糊处理,对观测并没有进行尺度模糊处理。
| $HK=POD-F$ | (4) |
Roberts等(2008)提出了一种直接比较预报和观测在窗区内格点覆盖百分比的检验方法。该方法认为,只要预报和观测对于某一事件发生的频率是相近的,就是一个有用的预报。最初他们定义了Fractions Brier Score (FBS),
| $FBS=\frac{1}{N}\sum\limits_{N}{{{\left( {{\left\langle {{P}_{y}} \right\rangle }_{s}}-{{\left\langle {{P}_{x}} \right\rangle }_{s}} \right)}^{2}}}$ | (5) |
在FBS评分的基础上,可以计算Fractions Skill Score (FSS)
| $\begin{align} &FSS=1-FBS/\left\{ \frac{1}{N}\left[ \sum\limits_{N}{{{\left( {{\left\langle {{P}_{y}} \right\rangle }_{s}} \right)}^{2}}} \right. \right.+ \\ &\left. \quad \quad \quad \left. \sum\limits_{N}{{{\left( {{\left\langle {{P}_{x}} \right\rangle }_{s}} \right)}^{2}}} \right] \right\} \\ \end{align}$ | (6) |
式中第二项的分母项是最差预报的情形,即预报和实况完全没有重叠的部分。FSS评分的范围从0到1,其中0为完全不正确预报,1为完美预报情形。
2 不同对流回波形态的模糊检验研究为了考察模糊检验方法在不同形态的对流系统预报检验中的性能,选取了雷暴单体型、飑线型和大范围降水型三类典型对流系统的个例,对SWAN和NoCAWS的1 h回波外推预报进行模糊检验。
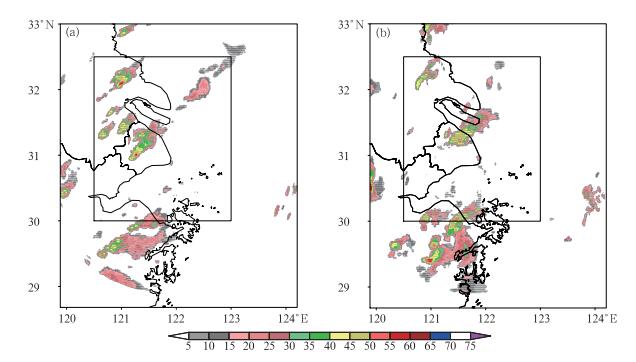
2.1 2013年9月13日局地雷暴天气2013年9月13日午后到夜里,自上海的东北向西南依次出现了短时强降水和雷雨大风天气,其中部分地区的降水量级达到了大暴雨标准。以08:16(世界时,下同)的一次1 h回波外推预报为例,对该时次预报进行了模糊检验试验。图 2中的矩形区域为预报的检验范围(下同)。从雷达回波的形态上来看,主要是零散发展的孤立多雷暴单体。对此次过程的分析指出,阵风锋和低涡切变线相交处的强辐合造成了此次强对流西南向的后向传播特点,同时露点锋的动力抬升作用也有利于对流向西南方向传播(孙敏等,2015)。从图 2可以看出,回波外推预报不能有效地刻画雷暴的后向传播特点,预报的雷暴位置与初始时刻相比静止少动(图略),且漏报了上海以西地区的新生雷暴单体。
|
图 2 2013年9月13日一次局地雷暴过程的NoCAWS雷达反射率实况(a)与1 h反射率外推预报(b) (单位:dBz) Fig. 2 The radar reflectivity (unit: dBz) observation (a) and 1 h extrapolation forecast (b) provided by NoCAWS during a local storm on 13 September 2013 |
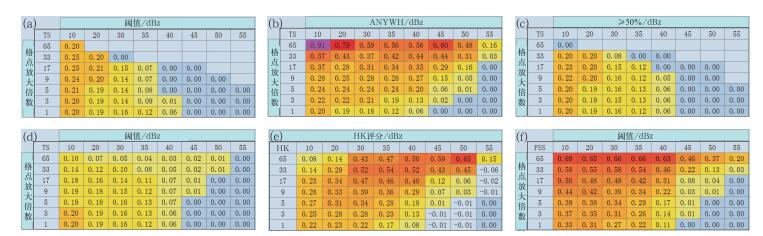
图 3给出了6种尺度模糊检验的结果,窗区尺度即格点放大倍数,单位为km,下同。其中各个方法的表格最底部一栏,即窗区尺度为1 km时,也就是传统的TS检验方法的结果,即点对点一一对应的检验。从升尺度检验来看,预报在低阈值、较大窗区尺度时,TS评分较高;在高阈值、大窗区尺度时,TS评分较低(或者没有样本)。这是因为升尺度方法是在一定的空间尺度上进行了取平均值处理,必然会造成高阈值样本的衰减和低阈值样本的增加。当尺度增加的时候,对于弱降水回波,预报与实况的吻合度有所增加。
|
图 3 对2013年9月13日08:16的NoCAWS 60 min雷达回波外推预报的模糊检验 (a)升尺度法,(b)anywhere标准的最小比例法,(c)50%标准的最小比例法,(d)模糊逻辑法,(e)多事件列联表,(f)FSS Fig. 3 Fuzzy verification on 60 min NoCAWS radar reflectivity extrapolation forecast at 08:16 UTC 13 September 2013 (a) upscaling, (b) anywhere for minimum covrege, (c) 50% for minimum coverage, (d) fuzzy logic, (e) multi-event contingency table, (f) fraction skill socre |
对于最小比例法,图 3b给出了最小比例临界值(anywhere)时的检验结果,即对于某一事件,选择的窗区范围内只要一个格点发生,即判定该事件发生。图 3c的判别比例值为50%,即当选择的窗区范围内至少有50%的格点发生该事件,才判定该事件发生。对于anywhere的判别标准来看,当尺度增加时,对于不同的阈值,TS评分均有显著的增加,如对于≥10 dBz的回波,当窗区尺度在65 km时,TS评分从33 km时的0.57跃升至0.91。因为当尺度增大时,实况和预报的窗区内仅需要一个格点有某一事件发生即判定预报准确,是比较容易的。而对于50%的比例,满足该判别标准本身是比较困难的,即对事件是否发生的判断比较严苛,因此某一事件的样本必然较少。对于低阈值,当尺度在17 km左右时,TS评分最高;随着阈值的增加,最高TS评分所在的尺度要更小一些;当阈值达到一定范围时未做尺度模糊处理的传统检验方法得分更高。因为对于较大的窗区尺度而言,50%的比例意味着较大范围的降水,而本小节选取的是孤立零散发展的雷暴单体,在高阈值、大窗区尺度时样本稀少,预报本身又存在一定的偏差,因此TS评分偏低(或者没有样本)。比例的选择应该与检验对象的尺度匹配。对于尺度较小的对流单体,当窗区尺度较大时,此时应该选择较低的比例,否则检验对象无法满足预报判定的要求,检验也失去意义,如高阈值、65 km窗区尺度时。
对于模糊逻辑方法,由于考虑了观测和预报在空间上的概率分布,对传统的0、1型二分类列联表进行了概率化处理,因此模糊逻辑方法是倾向于给传统意义上好的预报一定的“惩罚”,而给差的预报一定的“奖励”(Ebert,2002)。从图 3d可以看出,低阈值时,随着窗区尺度的增大,TS评分下降;高阈值时,随着窗区尺度的增大,TS评分上升;中间阈值时,最高TS评分分布在中间尺度。对于本小节中的雷暴单体个例,当窗区尺度较大时,该窗区内的概率分布函数峰值将向纵轴(x=0) 靠近,即在低值区间的P(x)更大。因此,低阈值时,TS评分相对于传统检验方法有显著的下降。而对于高阈值,传统检验方法中的命中率为0;在模糊逻辑方法中,当窗区尺度较大时,至少给予了非常小的概率,TS评分略高,即对较高等级的气象要素,在放松尺度要求时可以提高评分。可见,这类检验方法对尺度小且预报难度较大的强对流天气预报来说,可以挖掘一些潜在的价值,特别是当用户只需关注其强度而不是空间准确率时。
多事件列联表方法有些类似于anywhere标准的最小比例法,不同的是,在这里观测的格点是确定的,并没有做尺度模糊处理,只对预报格点进行尺度模糊处理。从图 3e HK评分来看,在低阈值时,最高HK评分所在的尺度在9~17 km,表明预报对降水系统的位置存在着一定的偏差。随着阈值的增加,最高HK评分所在的窗区尺度逐渐增加。一般地,随着搜索半径的增加,命中率和虚警率必然同时增加,当命中率的增加占主导时,HK评分自然就较高。这也意味着,此次预报虽然存在着一定的偏差,但在强度上与实况是有一定的匹配度的。
FSS方法主要是比较预报和实况在一定的范围内的发生频率。从图 3f可以看到,随着窗区尺度的增加,预报和实况有了更多的机会互相匹配,因此当尺度较大时,FSS评分相应地较高。
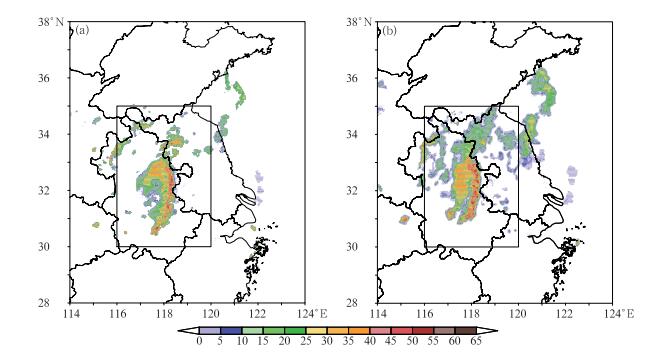
2.2 2014年7月30日飑线天气过程与零散的雷暴单体不同,2014年7月30日的个例为一次较大范围的飑线过程。SWAN的1 h雷达回波外推预报的飑线位置与实况比较接近,但形态有较大差异,范围偏大且结构较松散,空报了江苏和安徽北部的弱降水(图 4)。
|
图 4 2014年7月30日一次飑线过程的SWAN雷达回波实况(a)与1 h外推预报(b) (单位:dBz) Fig. 4 The radar reflectivity (unit: dBz) observation (a) and 1 h extrapolation forecast (b) provided by SWAN during a squall line process on 30 July 2014 |
图 5给出了6种模糊检验方法的结果,由于是较大范围的飑线过程,与孤立的雷暴单体相比,总体上预报在低阈值上有更高的TS评分。从升尺度和50%标准最小比例法的结果来看,低阈值时,预报在更大的尺度上拥有更高的TS评分,当阈值增大时,最高TS评分所在的尺度变小。Anywhere标准的最小比例法TS评分的分布与雷暴单体的类似,当尺度增加时,预报与实况有了更多匹配的机会,TS评分较高。从传统的检验方法来看,飑线个例的TS评分明显高于雷暴单体个例,而当尺度达到65 km时,对于anywhere标准的最小比例法,两者的TS评分已大致相当。

|
图 5 对2014年7月30日16:24的60 min SWAN雷达回波外推预报的模糊检验 (a~f)同图 3 Fig. 5 Fuzzy verification on 60 min SWAN radar reflectivity extrapolation forecast at 16:24 UTC 30 July 2014 (a-f) Same as Fig. 3 |
从模糊逻辑方法来看,对于大部分阈值,最高TS评分均在1 km尺度上;只有当阈值达到50 dBz时,最高TS评分所在尺度才位于17 km,与飑线东西向的尺度相当。低阈值时,TS评分相对于传统检验方法虽然有所下降,但幅度小于雷暴单体个例。而对于高阈值,传统检验方法的命中率非常低;在模糊逻辑方法中,当窗区尺度较大时,TS评分有所增加。
从多事件列联表的结果来看,低阈值时,最高HK评分所在的尺度为5 km左右,表明预报对降水回波的整体位置把握基本准确。当阈值增加时,最优搜索半径也随之增加,与雷暴单体类似,但变化幅度较小,高阈值时,最优搜索半径在33 km左右,表明相对于雷暴单体的预报,飑线的预报位置偏差要更小一些。
FSS评分的分布与雷暴单体个例类似,均在更大的尺度上有着更高的得分,且对于大部分阈值,此次飑线过程的预报得分更高。
2.3 2013年10月7日“菲特”大暴雨天气过程2013年10月7日的降水过程是台风菲特登陆后的残余低压与冷空气互相作用引起的强降水过程。从雷达回波来看(图 6a),此次过程是大范围的降水过程,“菲特”与冷空气互相作用激发的一条南北向的中尺度强降水带从东向西扫过上海地区。预报的雨区(图 6b)和强回波带与实况基本一致,其上大于40 dBz的回波位置有所差异。从回波垂直结构上看,呈现出暖性、低质心的特征(邵晨等,2013)。

|
图 6 2013年10月7日“菲特”大暴雨的NoCAWS雷达回波实况(a)与1 h外推预报(b) Fig. 6 The radar reflectivity observation (a) and 1 h extrapolation forecast (b) provided by NoCAWS during the extremely heavy rain of Typhoon Fitow on 30 July 2014 |
图 7给出了针对此次过程的模糊检验结果。从传统检验结果来看,由于是台风残余低压与冷空气结合引起的大范围系统性强降水,因此整体上此次过程的预报评分要高于前两次过程。对于升尺度方法,10~20 dBz阈值,TS评分在65 km尺度上最高;30~35 dBz阈值,TS评分在33 km尺度上最高;40~45 dBz阈值,TS评分在1 km尺度上最高。
|
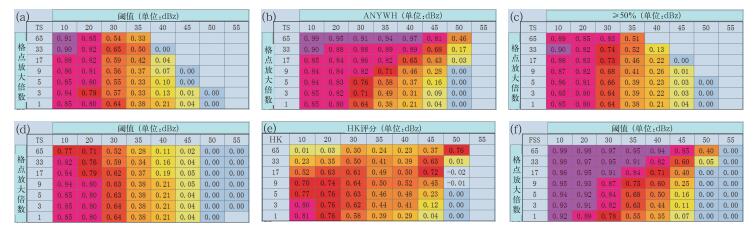
图 7 对2013年10月7日21:29的NoCAWS60 min雷达回波外推预报的模糊检验 (a~f)同图 3 Fig. 7 Fuzzy verification on 60 min NoCAWS radar reflectivity extrapolation forecast at 21:29 UTC 7 October 2013 (a-f) Same as Fig. 3 |
从≥50%标准的最小比例法来看,TS评分分布与升尺度方法也类似,其中40 dBz阈值,最高TS评分在9 km尺度。一方面表明此次过程降水样本在空间分布和强度分布上均较充足,为一次大范围强降水过程,另一方面也表明预报与实况在不同尺度上的匹配度也较高。
从模糊逻辑方法来看,TS评分的分布与飑线个例比较相似,对于10~40 dBz阈值,最高TS评分均在1 km尺度上;对于45 dBz阈值,最高TS评分在9~17 km。这也表明,基于模糊逻辑的思想,对于10~40 dBz阈值,预报整体上都较好。
从多事件列联表方法来看,HK评分的分布与飑线过程类似,但随着阈值的增加,最高TS评分所在的尺度增幅较小,且得分更高。表明预报与实况的位置偏离并不大,当搜索半径过大时,使得虚警率的增加更加明显,从而导致HK评分下降。
与雷暴单体和飑线两个个例相比,FSS评分在大部分尺度和阈值上均较高。
2.4 不同回波形态模糊检验结果的对比分析从前文所述的三个不同回波形态个例检验结果的对比分析来看,由于预报对象特点和预报水平的制约,在各类得分以及得分的分布上存在着一定的差异。升尺度方法是在一定的空间尺度上进行平均,50%判别标准的最小比例方法是在一定的空间尺度上提高对事件发生与否的判别标准,因此这两者对预报对象的样本数量和分布都比较敏感,由于空间的平滑作用,一般在高阈值、大尺度上TS评分较低;而对于低阈值,TS评分一般随着尺度的增大而增加。
对于anywhere标准的最小比例法,预报和实况更容易匹配,一般随着尺度的增加,TS评分也随之增加。理论上,当尺度足够大时,预报的TS评分应该接近完美预报(TS=1)。从中等强度和高强度阈值来看,“菲特”和飑线个例在65 km,均有较高的评分,而雷暴单体个例的TS评分较低,表明雷暴单体的预报水平较低,即使尺度大、判定标准低,预报得分仍处于较低水平。
从模糊逻辑方法TS评分的分布来看,随着阈值和尺度的增加,雷暴单体个例的最高TS评分所在的尺度线性增大;飑线个例的TS评分在低阈值时,随着尺度的增加,TS评分基本无变化,但当尺度增加至33和65 km时,TS评分开始下降,在高阈值时,高TS评分分布在大尺度区间;“菲特”个例与飑线类似,从低阈值到中等强度阈值,最高TS评分也倾向于分布在较小的尺度上。一般当尺度增加时,模糊逻辑方法倾向于给观测和预报变量的空间分布更大的不确定性表述,因此容易给“好”的预报更多的惩罚,这也表明飑线和“菲特”个例的预报在传统意义上具有更高的技巧。对于低阈值,随着窗区尺度的增加,三个个例的TS评分都呈下降趋势,但下降幅度有差异,雷暴单体的降幅最大,而“菲特”个例的降幅最小,这与预报对象的空间分布密切相关,“菲特”的降水回波分布范围更广,对于一定的窗区尺度,概率分布函数更尖锐,不确定性更小,而雷暴单体的不确定性更大。
多事件列联表方法只对预报进行了尺度放大处理,而观测还是原始格点。对于三个个例,低阈值时,最高HK评分所在尺度较小,随着阈值的增加,最优尺度也随之增加。对比发现:当预报位置和强度存在着较多的偏差或漏报时(高阈值),一般需要更大的搜索半径;当预报较理想时(低阈值时的飑线和“菲特”个例),更大的搜索半径使得虚警率的增加更加明显,从而导致HK评分降低。
FSS方法的分布特征在三个个例中并无明显差异。该方法在对不同预报提供者在不同尺度上的预报技巧进行比较时,可能更有实用价值。
总之,对于模糊检验方法,分级预报评分在尺度和阈值的分布既有预报提供者自身预报技巧的影响,也有被检验对象自身形态造成的样本制约。
3 三类理想强对流模型的模糊检验试验从前文所述的三个个例检验结果来看,预报对象自身的分布特点对模糊检验的结果也有一定的影响。一些文献中的理想个例选取了圆形或椭圆形分布的对象进行检验方法的对比试验(Ebert,2002),本文为了进一步研究空间模糊检验方法在不同情形下的表现,结合强对流天气的特点,通过构造单体、飑线和大范围降水三种理想的强对流模型,并给予预报不同的距离偏差,来考察文中涉及的多种模糊检验方法的表现,以及与传统检验方法的差别,为用户更好地应用模糊检验结果提供依据。
构造的雷暴单体模型为椭圆状,尺度约为40 km,模拟的距离误差为0~100 km。飑线模型的南北向尺度约为150 km,东西向尺度约为30 km,模拟的距离误差同样为0~100 km。大范围降水模型的尺度约为300 km,并包含有两个>10的高值中心,鉴于检验目标的尺度较大,检验区域也更大,模拟的距离误差则为0~300 km(图 8)。

|
图 8 雷暴单体型(a)、飑线型(b)和大范围降水型(b)的理想模型示意图 (等值线为0、5、10、15;空间分辨率为1 km;矩形区域为检验区域) Fig. 8 The ideal model diagrams of thunderstorm cell (a), squall line (b) and large-scale heavy rain (c) (Contour line is for 0, 5, 10, 15, and spatial resolution is 1 km. Rectangle area indicates the verification scope) |
以10 km的距离偏差为例(图 9),从不同类型的三个预报对象来看,一般地,随着窗区尺度的增加,TS评分下降,而对于>0的阈值,范围较小的单体和飑线模型,TS评分随着窗区尺度的变化有一个先减小后增加的过程,最高TS评分所在的尺度约是33 km,与模型本身的尺度大致相当。当窗区尺度与模型本身的尺度相当时,由于模型中心值相对较高,升尺度方法使得某些预报或实况为0的格点有机会成为满足>0阈值的格点,因此TS评分有所上升。对于飑线,考虑到南北向的平滑作用,>0阈值的最高TS评分所在的尺度更大,在65 km。
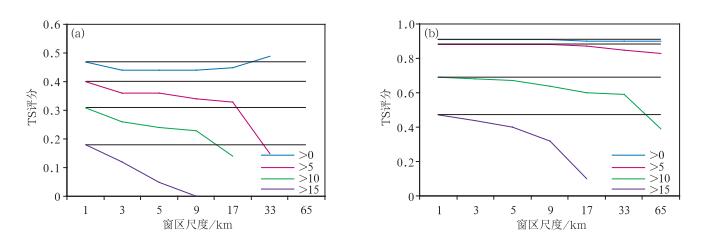
|
图 9 距离偏差=10 km时,单体模型(a)和大范围降水模型(b)在不同窗区尺度下的TS评分 (黑实线表示传统检验方法TS评分) Fig. 9 TS scores at different neighborhoods of thunderstorm cell (a) and large scale heavy rain (b) forecast with 10 km distance bias (Black solid lines indicate traditional TS score, while the colored lines indicate upscaling method) |
图 10给出了不同窗区尺度下,单体模型的升尺度TS评分与传统TS评分随距离偏差的变化。从图中可以看到,当窗区尺度为5 km时,升尺度方法的TS评分均要小于传统的TS评分。当窗区尺度达到33 km时,>0阈值的TS评分要高于传统TS评分,>5阈值的TS评分低于传统评分;对于10及其以上阈值,尺度较小的单体模型出现了无样本的情况。对于飑线型,TS评分的分布与单体类似(图略)。对于大范围降水模型,所有升尺度后的TS评分均低于传统评分。因此,对于孤立的、高阈值的强对流系统,在大窗区尺度时,升尺度方法容易造成样本的衰减和丢失,可能不太适用;而对于低阈值的情况,升尺度方法的评分则更具有适用性,特别是大范围的弱降水系统。
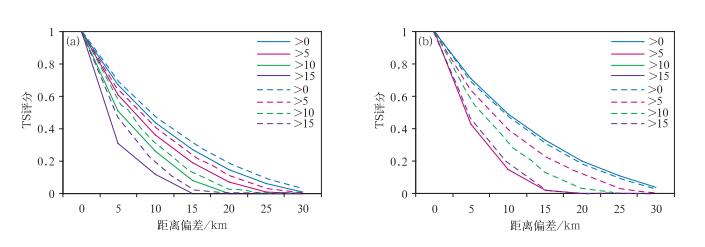
|
图 10 当窗区尺度为5 km(a)和33 km(b)时,单体模型的TS评分随距离偏差的变化 (实线为模糊检验结果,虚线为传统检验结果) Fig. 10 TS score of thunderstorm cell model at different distance bias for neighborhood of 5 km (a) and 33 km (b) (Solid lines indicate fuzzy verification, while dashed lines are for the traditional results) |
最小比例法首先需要对预报事件是否发生进行判定,这个判定标准是由用户根据自己预报检验的需求而定。根据模拟试验结果,最小比例法获得的TS评分分布以及与传统TS评分的比较均受到判别标准的影响。对于anywhere标准,三种模型的检验结果表明,随着窗区尺度的增加,TS评分均有显著上升,特别是当距离偏差较大时。对于大范围降水,由于基础的传统TS评分高,TS评分虽然也有上升的趋势,但幅度趋小。同时应该注意到,当距离偏差足够大时,“点对点”的传统检验方法TS评分均为0,而最小比例法在较大的尺度上仍然能给出相应的有效的TS评分。因此该标准在检验强对流单体(高阈值、小尺度)时,具有较高的应用价值。
当判别标准为30%时,TS评分分布的变化趋势与anywhere标准时相似,即随着窗区尺度的增加,TS评分上升,但增加幅度显著减小。综合比较而言,飑线模型的TS评分相对于传统检验方法增加幅度最高。这与飑线的线状结构和尺度大小有关。
当判别标准为50%时,TS评分分布的变化趋势与anywhere和30%标准有较大差异。对于单体和大范围降水模型而言,随着窗区尺度的增加,TS评分均出现不同程度的下降;而飑线模型,随着窗区尺度的增加,TS评分仍呈上升的趋势,但增加幅度很小。在不同的距离偏差下,飑线模型的TS评分仍要高于传统方法,而单体模型的TS偏低。图 11给出了当窗区尺度为33 km时TS评分的分布,对于10及其以上阈值,单体和飑线模型已经无样本。
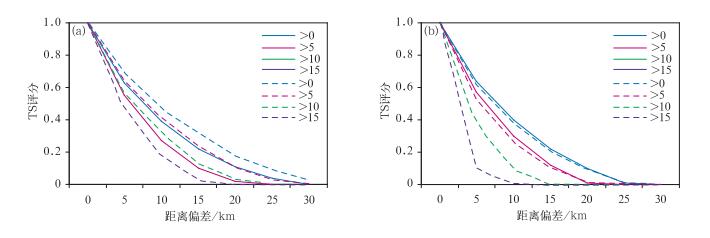
|
图 11 当窗区尺度为33 km时,对于50%的判别标准,单体(a)和飑线(b)模型的最小比例法TS评分随距离偏差的变化 (实线为模糊检验结果,虚线为传统检验结果) Fig. 11 TS score of thunderstorm cell (a) and squall line (b) model at different distance bias for neighborhood of 33 km with 50% coverage (Solid lines indicate fuzzy verification, while dashed lines are for the traditional results) |
对比表明,对于最小比例法,飑线模型的TS评分的变化趋势与另外两个模型有所差异,主要体现在30%和50%的判别标准上,这主要是由于飑线模型的“月牙”型分布引起的,在飑线附近,能有更多的格点在不同的窗区尺度上满足前文所述的两个判别标准。当对预报事件的判别标准较高时(如30%、50%),与升尺度方法类似,最小比例法在高阈值、大窗区尺度时,出现样本的衰减和丢失。
3.3 模糊逻辑法对于单体模型(图 12),相对于传统检验方法,当距离偏差为10 km时,随着窗区尺度的增加,不同阈值的TS评分均呈现下降的趋势;当距离偏差为20 km时,对于低阈值(>0) 时,随着窗区尺度的增加,TS评分有所下降,而对于5~15等级的阈值,TS评分呈先上升后下降的趋势,不同的阈值TS评分峰值出现的尺度有所差异。当距离偏差较大或预报对象尺度较小(相应的距离偏差也较大)时,TS评分峰值所在的尺度较大。即需要更大的窗区尺度使预报和实况匹配。对于飑线模型,与单体模型相比,由于其东西向的尺度更小,因此也在更小的距离偏差和更低的阈值上,就出现这种先上升后下降的趋势。而对于大范围降水模型,当距离偏差较小时(0~20 km)时,随着窗区尺度的增加,TS评分均呈下降趋势,当偏差较大时,也开始呈现先上升后下降的趋势。对于三个模型,当距离偏差足够大时,最高的TS评分总是在更大的窗区尺度上获得的。
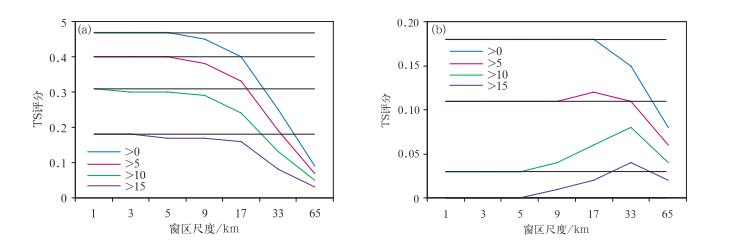
|
图 12 距离偏差=10 km(a)和20 km(b)时,单体模型在不同放大直径下的模糊逻辑TS评分 (黑实线表示传统检验方法TS评分) Fig. 12 TS scores of thunderstorm cell forecast at different neighborhoods with 10 km (a) and 20 km (b) distance bias (Black solid lines indicate traditional TS score, while the colored lines indicate fuzzy logic method) |
图 13给出了当窗区尺度为33 km时,单体和大范围降水模型的TS评分随距离偏差的变化。飑线模型的TS评分分布与单体类似,当距离偏差较小时,低于传统检验方法;随着偏差的增大,模糊检验法的TS评分逐渐高于传统检验方法。大范围降水总体的分布特征与前两者类似,但变化幅度小。这与检验对象的空间分布特征有关。对于给定的窗区尺度,大范围降水模型中对TS评分有贡献的大部分格点的概率分布函数呈尖锐型,即预报和实况的不确定性小,TS评分变化幅度小;而单体和飑线模型中大部分格点的概率分布函数呈宽广型,即预报和实况具有较大的不确定性,TS评分变化幅度大,与实际个例一致。即使对于偏差为0的完美预报,模糊逻辑法的TS评分均小于1。以>0阈值,33 km尺度为例,大范围降水模型的完美预报TS评分为0.86,而单体模型的TS评分则低至0.3。由此可见,模糊逻辑方法的完美预报评分在一定程度上还能反映预报对象本身在空间分布上的特征。如果预报对象为数值相等的均一场时,则完美预报的TS评分为1。另一方面,当预报的偏差足够大时,传统的TS评分为0,而模糊逻辑法因为给予“差”的预报一定的奖励,使之仍能获得一定的评分,就有区分“一般差”与“更差”预报的能力,可能挖掘出潜在的应用价值,在某种程度上相当于拓展了预报检验的应用范围。
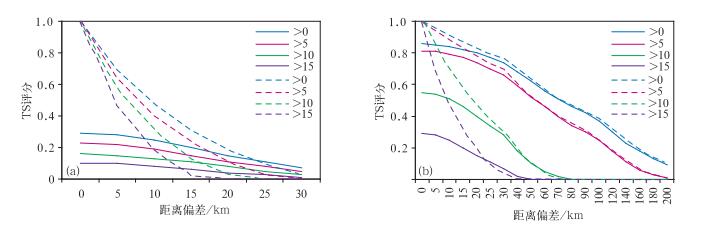
|
图 13 当窗区尺度为33 km时,单体(a)和大范围降水(b)模型的TS评分随距离偏差的变化 (实线为模糊检验结果,虚线为传统检验结果) Fig. 13 TS score of thunderstorm cell (a) and large scale heavy rain (b) model at different distance bias for neighborhood of 33 km (Solid lines indicate fuzzy verification, while dashed lines are for the traditional results) |
对于多事件列联表,在三种情形下,HK评分的分布比较相似。一般地,当距离偏差较小时,随着窗区尺度的增加,HK评分呈现一个先上升后下降的趋势,且随着距离偏差的增加,最高HK评分所在的尺度也相应地增加。当距离偏差达到一定程度时,最高HK评分总是在最大的窗区尺度上获得。这是因为构造的预报偏差以位置偏差为主,而未涉及强度误差,因此当搜索半径足够大时,总是能获得匹配的预报,命中率总是趋近于1的。
图 14给出了当窗区尺度为33 km时,单体和大范围降水模型的HK评分随距离偏差的变化。总体来看,当距离偏差为0或较小时,多事件列联表的HK评分要略低于传统检验方法;当距离偏差增大时,HK评分要高于传统检验方法;但当距离偏差足够大时,多事件列联表的HK评分与传统检验方法相当或略低,此时HK评分一般都接近0或负。对于大范围降水模型,由于检验对象自身的尺度相对较大,33 km的窗区尺度与检验对象相比并不大,因此低阈值时,多事件列联表的HK评分与传统检验方法较为接近。对于完美预报而言,传统点对点检验的命中率已经为1,增加搜索半径只会使虚警率增加,因此多事件列联表的HK评分要低于传统检验方法。当给予预报一定的距离偏差时,增加搜索半径,将使得命中率的增加占据主导,相应地提高HK评分。
3.5 Fraction Skill Score(FSS)对于FSS方法,三个模型的评分分布特征基本一致,即随着窗区尺度的增加,预报的得分总是增加的趋势,但幅度的大小受到基础得分的限制(传统的点对点检验)。当预报偏差较大时,随着窗区尺度的增加,FSS的增加也是显著的。但这种分布特征仅限于只考虑距离偏差的理想模型下。
3.6 试验结果分析与讨论从构造的三种常见强对流回波模型检验的理想试验来看,文中所述的五种模糊检验方法各有特点,适用范围也有差异。每种方法的前提和关注点都不一样,需要用户根据自己需求进行选择。
由于升尺度方法的平滑作用,对于孤立的、高阈值的强对流系统,在较大的窗区尺度时,该方法容易造成样本的衰减和丢失,可能不太适用。而对于低阈值的情况,升尺度方法的评分则更具有适用性,特别是大范围的弱降水系统。
对于最小比例法而言,anywhere的判别标准更适用分散、孤立发展的雷暴单体或者其他高阈值事件。如果用户更关注具有一定空间尺度的强降水预报能力,则需要提高相应的判别标准与窗区尺度。
模糊逻辑方法的适用范围较广,对预报和实况本身的空间分布特征比较敏感。主要反映在某种降水形态下,预报在何种尺度上是较优的。一般地,传统意义上“好”的预报倾向于在小尺度上获得高评分,“差”的预报倾向于在大尺度上获得高评分。因此,当传统得分较低的预报在大尺度上获得较高的评分时,用户应该注意到,基于当前预报和实况的空间分布,该预报仍然有一定的应用价值。
多事件列联表方法对观测未做尺度放大处理,因此相当于是以观测点作为观察坐标。该方法在检验分散性、高阈值的强对流事件预报时具有较高的应用价值。
理想试验的模拟还表明,对于各种模糊检验方法,当确定窗区尺度后,随着距离偏差的增加,正向性的评分总是呈现递减的趋势,说明模糊检验方法是公正和客观的,能够对预报的优劣进行认定。另一方面,相对于传统检验方法,模糊检验的价值不仅仅体现在基于不同评价策略的多元化信息,还在于当预报偏差达到一定程度时,传统检验方法只能给出0评分,而多种模糊检验方法仍然能够给出有效的评分,对这些预报给出客观公正的评价,对用户有一定的参考价值。
4 结论针对强对流天气预报的特点,本文引入了模糊检验的思想,并介绍了常用的五种模糊检验方法,并以SWAN和上海市气象局NoCAWS 1 h雷达回波外推预报为例,针对强对流天气三种常见的类型,雷暴单体、飑线和大范围系统性强降水,分别进行了模糊检验试验,还构造了对应的三种典型强对流回波模型,给予预报不同的距离偏差,开展理想试验。结果表明:
(1) 相对于“点对点”的传统检验方法,模糊检验能够基于不同的评价策略上给出预报在不同尺度上的更多信息,给予预报更加全面和客观的评价。
(2) 模糊检验方法对不同类型的强对流天气系统有不同的反映。针对不同的评价策略,同一个预报的最优尺度是有差异的。模糊检验方法的本质是从用户需求的角度出发,提供多元化的预报检验思路。因此用户应该根据自己对预报产品的应用特点以及需求,设计和确定合适的检验方法,如类似于升尺度方法的窗区平均方法,也可以在不同的尺度上进行求最大值、最小值、百分位等处理。
(3) 结合实际个例和理想试验,对于低阈值、大尺度事件,升尺度方法、高判别标准的最小比例法等方法均有一定的应用价值;对于高阈值、小尺度的强对流事件,传统检验方法经常不能给出有效的评分或者评分偏低,而低判别标准的最小比例法、模糊逻辑法和多事件列联表则更有应用价值。
(4) 从理想试验结果来看,当预报偏差达到一定程度时,传统检验方法只能给出区分度较小的低评分或0评分,多种模糊检验方法仍然能够给出有效的评分,相当于拓展了预报检验的适用范围。
模糊检验方法在预报检验中的应用在国内还尚未普及,如何更好地应用该方法还需要大量的基础性研究工作。需要说明的是,本文的检验结果只是针对几个典型的强对流回波形态,对各种模糊检验方法的研究还需要后期大量的样本积累和理想型试验,才能对各检验方法的特点和应用有更全面的认识。模糊检验方法还可以应用到高分辨数值预报模式的检验,空间尺度的模糊处理也为不同分辨率的数值预报模式检验对比提供了一种新的思路。通过不同模式的对比,将对模糊检验方法有更多系统性的认识,能够让用户更好地应用数值预报模式,也有利于模式开发人员更好地改进模式性能。
模糊检验方法种类繁多,每种方法都各有特色。面对模糊检验方法产生的大量信息,需要用户根据预报检验的目的,有所取舍。同时用户也需要根据自己对正确预报的认定策略选择需要的模糊检验方法,避免被过多的方法和信息“乱花迷眼”。
戴建华, 茅懋, 邵玲玲, 等, 2013. 强对流天预报检验新方法在上海的应用尝试[J]. 气象科技进展, 3(3): 40-45. |
符娇兰, 宗志平, 代刊, 等, 2014. 一种定量降水预报误差检验技术及其应用[J]. 气象, 40(7): 796-805. DOI:10.7519/j.issn.1000-0526.2014.07.003 |
刘凑华, 牛若芸, 2013. 基于目标的降水检验方法及其应用[J]. 气象, 39(6): 681-690. DOI:10.7519/j.issn.1000-0526.2013.06.003 |
邵晨, 郭品文, 戴建华, 2013. 上海短历时强降水的雷达和闪电活动特征[J]. 热带气象学报, 29(4): 656-664. |
孙敏, 戴建华, 袁招洪, 等, 2015. 双多普勒雷达风场反演对一次后向传播雷暴过程的分析[J]. 气象学报, 73(2): 247-262. DOI:10.11676/qxxb2015.012 |
尤凤春, 王国荣, 郭锐, 等, 2011. MODE方法在降水预报检验中的应用分析[J]. 气象, 37(12): 1498-1503. DOI:10.7519/j.issn.1000-0526.2011.12.004 |
Atger F, 2001. Verification of intense precipitation forecasts from single models and ensemble prediction systems[J]. Nonlinear Processes in Geophysics, 8: 401-417. DOI:10.5194/npg-8-401-2001 |
Damrath U. 2004.Verification against precipitation observations of a high density network -what did we learn?//International verification methods workshop, Montreal, 15-17 September 2004. (http://www.cawcr.gov.au/projects/verification/Workshop2004/presentations/5.3_Damrath.pdf).
|
Davis C, Brown B, Bullock R, 2006. Object-based verification of precipitation forecast[J]. Part I: Methodology and application of mesoscale rain areas. Mon Wea Rev, 134: 1772-1784. |
Ebert E E. 2002. Fuzzy verification: Giving partial credit to erroneous forecasts.//NCAR/FAA Verification Workshop: Making Verification More Meaningful, NCAR, Boulder, 30 July-1 August 2002.
|
Ebert E E, 2008. Fuzzy verification of high-resolution gridded forecasts: A review and proposed framework[J]. Meteor Appl, 15: 51-64. DOI:10.1002/(ISSN)1469-8080 |
Mass C F, Ovens D, Westrick K, et al, 2002. Does increasing horizontal resolution produce more skillful forecasts?[J]. Bull Amer Meteor Soc, 83: 407-430. DOI:10.1175/1520-0477(2002)083<0407:DIHRPM>2.3.CO;2 |
Roberts N M, Lean H W, 2008. Scale-Selective verification of Rainfall Accumulations form high-resolution forecasts of convective events[J]. Mon Wea Rev, 136: 78-97. DOI:10.1175/2007MWR2123.1 |
Weygandt S S, Loughe A F, Benjamin S G, et al. 2004. Scale sensitivities in Model precipitation skill scores during IHOP. 22nd conference severe local storms. American Meteorological Society: Hyannis, MA, 4-8 October 2004.
|
Yates E, Anquetin S, Ducrocq V, et al, 2006. Point and areal validation of forecast precipitation fields[J]. Meteor Appl, 13: 1-20. |
Zepeda A J, Foufoula G E, Droegemeier K, 2000. Space-time rainfall organization and its role in validating quantitative precipitation forecasts[J]. J Geophy Res, 105(D8): 10129-10146. DOI:10.1029/1999JD901087 |
 2016, Vol. 42
2016, Vol. 42 

