2. 江苏省防雷中心,南京 210009
2. Jiangsu Lightning Protection Centre, Nanjing 210009
湿球温度是干燥器、冷水塔、空调和采暖通风等工程设计中重要的气象参数(中华人民共和国国家能源局,2012;中国气象局,2015)。随着气象现代化建设的发展,气象业务改革的深入,空气湿度的干、湿球温度的观测方式被自动观测方式所取代,湿球温度由直接观测变为通过计算间接而得,这给工程设计中湿球温度参数的分析及资料的连续性应用造成了一定困难,如何更为准确地计算湿球温度,成为了这一类工程应用中亟待解决的问题。
以往学者们(中国气象局,2015;荣剑文,2008;赵永胜等,2009;林婵等,2013;潘晓春等,2015;魏华兵等,2011)从不同的角度给出湿球温度的计算方法,构建的模型多采用迭代计算,但多为某一地区、较短时间内、定时观测资料的检验分析,对湿球温度持续性的(24时次)、长年代(几十年)的估算及其资料的连续性研究相对较少。为此本文采用牛顿迭代和最优逼近两种方法,讨论湿球温度的计算方法的估计偏差,并基于江苏省部分台站近40年的实测气象数据,对两种方法在长年代序列估计上进行检验分析。研究结果对湿球温度的简便计算及资料的连续性应用有一定参考意义。
1 资料江苏在2001—2004年逐渐停止观测湿球温度(王瑞等,2014),研究选取江苏省70个气象台站自建站以来至停止观测年份的湿球温度、干球温度(气温)、水汽压(相对湿度)、气压等气象要素的定时(逐时)观测资料作为基础研究数据。其中,为了减少观测仪器变更、观测规范沿革信息对估算结果分析的影响,研究以08、14和20时3个时次作为定时观测的统计样本;以1991年后百叶箱柱型的干、湿球温度表观测到停止湿球温度观测启用自动传感器的年份(2001—2014年),作为两种方法计算效果的检验时间序列,并在此基础上,进一步对13个气象台站建站(1951—1960年)至1990年的数据进行计算方法的长年代检验。
2 研究方法研究以牛顿迭代法和最优逼近法作为湿球温度计算的分析方法。
2.1 湿球温度计算中涉及的相关公式相关计算公式引自地面气象观测规范(中国气象局,2003)。
2.1.1 水汽压(1) 用干、湿球温度求空气中水汽压的计算公式:
| $ e = {E_t} - Ap({t_{\rm{d}}} - {t_{\rm{w}}}) $ | (1) |
湿球温度、水汽压即可以表示为:
| $ {t_{\rm{w}}} = {t_{\rm{d}}} - \frac{{{E_t} - e}}{{Ap}} $ | (2) |
| $ {E_t} = e + Ap({t_{\rm{d}}} - {t_{\rm{w}}}) $ | (3) |
(2) 空气中相对湿度:
| $ U = \frac{e}{{{E_{{t_{\rm{d}}}}}}} \times 100\% $ | (4) |
式中,td、tw分别为干、湿球温度(单位:℃);e、p、Et分别为水汽压、气压、湿球温度对应的纯水平液(冰)面饱和水汽压(单位:hPa);A为干湿表系数(单位:℃-1),由干湿表类型、通风速度、湿球是否结冰而定;U为相对湿度(单位:%);Etd为干球温度对应的纯水平液(冰)面饱和水汽压(单位:hPa)(中国气象局,2003)。
2.1.2 饱和水汽压在一定温度下,空气中的水汽与相毗连的水或冰平面处于相变平衡时湿空气中的水汽压,即饱和水汽压。采用世界气象组织推荐的戈夫-格雷奇(Goff-Gratch)公式(中国气象局,2003):
(1) 纯水平液面饱和水汽压
| $ \begin{array}{l} {\rm{log}}({E_{\rm{t}}}) = 10.79574\left({1 - \frac{{{T_1}}}{T}} \right) - 5.028{\rm{log}}\left({\frac{T}{{{T_1}}}} \right) + \\ 1.50475 \times {10^{ - 4}}\left({1 - {{10}^{ - 8.2969\left({\frac{T}{{{T_1}}} - 1} \right)}}} \right) + 0.42873 \times \\ \;\;\;\;\;\;\;{10^{ - 3}} \times ({10^{4.70955\left({1 - \frac{T}{{{T_1}}}} \right)}} - 1) + 0.78614 \end{array} $ | (5) |
(2) 纯水平冰面饱和水汽压
| $ \begin{array}{l} {\rm{log}}({E_{\rm{t}}}) = - 9.09685\left({\frac{{{T_1}}}{T} - 1} \right) - 3.56654{\rm{log}}\left({\frac{{{T_1}}}{T}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.87682\left({1 - \frac{{{T_1}}}{T}} \right) + 0.78614 \end{array} $ | (6) |
式中,T1为水的三相点温度,T1=273.16 K;T为绝对温度,T=t+273.15 K。
2.1.3 干湿表系数表 1给出了《地面气象观测规范》(中国气象局,2003)中的4种干湿表相应的A值,研究中采用现用百叶箱球状干湿表在风速为0.8 m·s-1时的系数。
|
|
表 1 干湿表系数表 Table 1 Psychrometric coefficients |
最优逼近法与牛顿迭代法均是以快速迭代对湿球温度进行估算,其中,牛顿迭代法是以温度(干球温度)为迭代变量,在湿球温度的合理范围内估算结果,迭代精度为0.001℃,为数学上的迭代误差;最优逼近法则是结合湿球温度的物理意义,以水汽压、湿球温度为迭代变量,模拟最佳符合水汽压的估算值,迭代精度即湿球温度的观测精度0.1℃。
2.2.1 牛顿迭代法湿球温度对应的饱和水汽压函数包含湿球温度的指数和对数,且式(2) 湿球温度等号两边均含有待求的湿球温度,函数关系复杂,难以直接求解,通过构造基于Taylor展开的牛顿迭代公式,分别对tw求导,结合饱和水汽压公式即可采用牛顿迭代法求解(林婵等,2013;潘晓春等,2015)。tw的迭代初值取td,成果误差取0.001℃。
2.2.2 最优逼近法最优逼近法是基于《工程项目采暖通风和空气调节气象参数分析技术指南》(中国气象局,2015)中湿球温度的求解方法,结合湿球温度、气压、温度(干球温度)、水汽压(相对湿度)的观测精度,对可能湿球温度取值范围进行0.5℃精度自高(干球温度)到低的快速扫描,迅速找到最小模拟误差的取值区间,并进行湿球温度正常精度(0.1℃)的逐个计算比较,以较少的计算量快速获得最接近于实测水汽压(相对湿度)记录值的计算值,即最佳模拟值。
考虑到计算模拟的过程会消去不同湿度仪器的差异,用于确定使用式(5) 和式(6) 的结冰条件统一简化为干球温度为0℃的界限(高于0℃为不结冰),而不使用观测记录湿球温度的结冰标志。相较于《工程项目采暖通风和空气调节气象参数分析技术指南》中计算全部15℃区域内0.01℃的全部模拟序列,研究所选用的方法在计算量上明显精减。
2.3 方法有效性检验指标研究选取平均绝对偏差、平均偏差、平均相对偏差、均方根偏差和符合率5个指标对计算方法的有效性进行检验(朱业玉等,2013;李亚丽等,2015;任芝花等,2015;朱艺青等,2016)。
(1) 平均绝对偏差(the mean absolute error,MAE):不考虑误差正负的情况下误差的平均大小,该值越小说明模型的模拟效果越好;
(2) 平均偏差(the mean bias error,MBE):考虑了误差的正负,能够反映出模型的高估或低估趋势及幅度,该值越接近于0,在一定程度上说明模型的模拟效果越好;
(3) 平均相对偏差(the mean percentage error,MPE):衡量模型的高估或低估趋势,避免了较大或较小观测值有较大或较小的绝对误差带来的影响,值越接近于0说明模型的模拟效果越好;
(4) 均方根偏差(the root mean square error,RMSE):放大了较大误差的影响,能够较好地反映误差的离散程度,值越小,数据的离散程度越低。
(5) 符合率:计算值与观测值相一致的数目占总样本数的比例,检验计算结果的符合情况。
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {|{{t'}_{i{\rm{w}}}} - {t_{i{\rm{w}}}}|} $ | (7) |
| $ MBE = \frac{1}{n}\sum\limits_{i = 1}^n {|{{t'}_{i{\rm{w}}}} - {t_{i{\rm{w}}}}|} $ | (8) |
| $ MPE = \frac{{100}}{n}\sum\limits_{i = 1}^n {\left({{{t'}_{i{\rm{w}}}} - {t_{i{\rm{w}}}}} \right)/{t_{i{\rm{w}}}}} $ | (9) |
| $ RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left({{{t'}_{i{\rm{w}}}} - {t_{i{\rm{w}}}}} \right)}^2}} } $ | (10) |
式中,t′iw为第i个湿球温度计算值,tiw为第i个湿球温度观测值,n为样本总数。
3 方法的计算效果检验 3.1 估算效果对比从江苏省湿球温度的偏差分析来看(表 2),1991年至湿球温度停止观测期间(2001—2004年),牛顿迭代和最优逼近两种方法的计算值较湿球温度观测值偏大,但程度均较小,远低于湿球温度的观测精度(0.1℃)。偏差分布主要集中在[-0.1℃,0.1℃],各站两种方法计算偏差落在该区间的比例分别为90.8%~100%和95.9%~100%,超过0.2℃的比重较少,说明两种方法的估算效果都不错。但从区间分布的符合率上来看,在70站11~14年的数据序列中,最优逼近法的估算结果有52站符合率达到100%,最低也在90.8%;而牛顿迭代法的绝对偏差主要集中在(0℃,0.1℃],符合率最高仅为20.1%(表略)。相较于牛顿迭代法0.001℃的计算精度,最优逼近与湿球温度观测精度相同的计算结果反而精度更高,系统性偏差小,这在均方根偏差、平均相对偏差的结果中亦可看到。可见,最优逼近法的计算结果优于牛顿迭代法,更接近观测值,符合率高,离散度低。
|
|
表 2 两种方法的绝对偏差分布统计 Table 2 Statistical distribution of absolute deviations by two different methods |
此外,值得注意的是,无论哪种方法的计算结果均存在着一定的区域性,台站之间的符合情况差异明显,因此,工程设计应用中应予以考虑湿球温度的地域性差异。
3.2 误差情况分析湿球温度的观测精度为0.1℃,故对于偏差>0.1℃的样本作进一步分析。表 3给出了计算偏差在不同区间出现的次数及最大偏大程度,两种方法样本数相同,计算偏差区间分布上一致性较好,均表现为正偏大次数较多,负偏差较少。但牛顿迭代的偏差数明显大于最优逼近法,且在(0.1℃,0.2℃]区间显著,偏大程度上牛顿迭代法亦较大,19站出现超过0.2℃的偏差,最优逼近法为13站,地域分布多在苏北以及沿江地区。
|
|
表 3 两种方法计算偏差区间分布统计 Table 3 Statistical distribution of calculated deviations by two different methods |
统计偏差>0.2℃的情况,最优逼近法共出现2110次, 绝对偏差 < 0.4℃; 牛顿迭代法出现2115次,程度较大,有6个时次>1℃(表 4),观测值与估算值的差值最大可达17.4℃。结合天气现象及各气象要素分析发现,5个时次前有降水出现,1个时次有雾,气温及气压相对变化较小,水汽压增大迅速(Δe≥6 hPa)。牛顿迭代法是以温度为迭代的函数,并未考虑水汽压本身的变化,致使估算结果出现非常大的偏差;而最优逼近法以水汽压作为逼近条件,考虑到其自身变化的影响,同期的估算并无偏差。可见,无论从物理意义还是结果上,最优逼近法对湿球温度的估算更合理,更加接近湿球温度的观测值。
|
|
表 4 计算偏差大于1.0℃的个例(单位:℃) Table 4 Cases with calculated deviations larger than 1.0℃ (unit: ℃) |
研究湿球温度的历史沿革信息发现,基准站南京站和吕泗站分别自1991和1988年开始24 h观测,且两站停止观测时间相同,因此选取1991—2004年进行逐小时偏差变化分析。相较于定时观测,逐时观测的偏差有所增大,但依旧较小,低于湿球温度的观测精度, 整体看最优逼近法的符合率(98.3%~98.5%)显著高于牛顿迭代法(19.3%~19.4%)。从符合率的日变化曲线来看(图 1a和1b),两者均呈单峰变化,且最优逼近的变化趋势相对明显,一天当中符合率以09—20时较高,日出前后较低。最优逼近符合率最高出现在吕泗14时,南京在13时,南京最低在05时,吕泗在07时,牛顿迭代的符合率最高出现在吕泗13时,南京14时,最低吕泗在03时,南京05时,这与湿球温度的日变化相似。
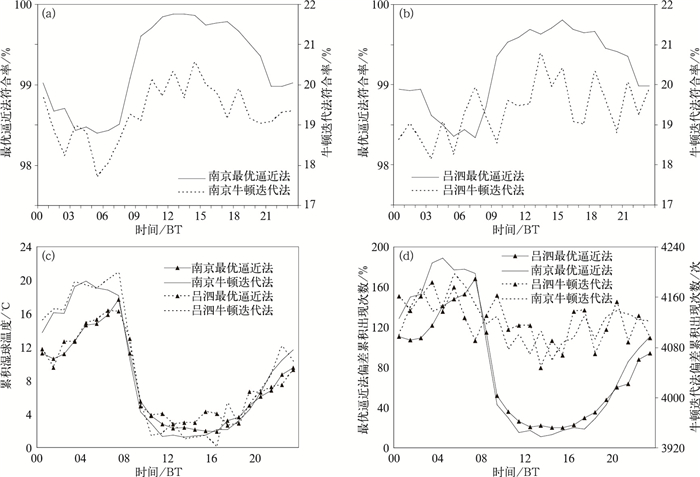
|
图 1 两种方法计算的符合率的日变化曲线南京(a)、吕泗(b)及相对应的累积偏差(c)与出现次数(d) Fig. 1 The daily variation curves of coincidence rate calculated by the two methods for Nanjing (a) and Lüsi (b), and cumulative deviation (c) and frequency (d) |
牛顿迭代偏差出现的频次远大于最优逼近,但由于计算精度不同,两者的累积误差相近(图 1c和1d)。最优逼近偏差的次数与累积偏差分布相似,而牛顿迭代法不同,考虑到两种方法的计算原理及精度,这也从另一侧面上反映出最优逼近估算的湿球温度符合率要远好于牛顿迭代。此外,虽然两种方法估算的累积湿球温度偏差变化相似,但在多数时次上,牛顿迭代的偏差程度较大,表现在南京和吕泗也略有不同,南京站以08、13、18、23时牛顿迭代估算偏大,11和17时最优逼近估算偏大;而吕泗站则以,10—17时、19—20时牛顿迭代估算偏大,22、23和01时最优逼近估算偏大。从图 1c和1d中还可以看出,南京站在夜间的累积偏差明显高于吕泗,白天却低于吕泗,与湿球温度观测情况的日变化相近,呈现出区域性的差异。
综上可见,最优逼近法估算的逐时吻合情况明显优于牛顿迭代,且更接近观测值的自身变化,在温度较高时符合率高,温度较低时符合率亦较弱。
4 长年代数据估算对比以上分析表明,计算方法能够较好地估计出湿球温度的观测值,最优逼近法的符合率非常好,显著优于牛顿迭代法。那么在长年代、不均一序列的湿球温度估算上两种计算方法的表现如何?为此,我们对江苏省13个拥有自建站以来至湿球温度停止观测近40年的时间序列数据进行了两种算法的长年代检验。
4.1 估算效果检验从长年代序列的估算结果来看,各项偏差均有所增大,但仍小于湿球温度的观测精度;两种方法的符合率都有所降低,偏差分布向两侧扩展,程度增大,绝对偏差>0.3℃出现次数增多(表 5)。分析发现各台站湿球温度的沿革信息多次变化, 仪器、观测规范以及干湿表系数等均有变更,直观反映出百叶箱柱状干湿表仪器类型的计算值与实际湿球温度的仪器观测值之间的差异,对照两种方法的计算偏差,最优逼近法偏差相对较小,符合率较高,说明在对近40年的原始长序列检验中,最优逼近法的估算结果离散度低,更接近观测值,符合情况优于牛顿迭代法。
|
|
表 5 建站至1990年计算偏差绝对值区间分布统计 Table 5 Statistical distribution of absolute deviations by different methods from the beginning to 1990 |
从近40年的长序列(图 2a)来看,1954年前和20世纪80年代湿球温度的估算偏差较大,且牛顿迭代估算误差大于最优逼近法的结果。结合沿革信息发现,两段时间的观测仪器与文中所选用时段不同,干湿表系数亦不同,可能是偏差增大的原因,但从量级来讲两个时段内的偏差仍较小,牛顿迭代估算在0.1~0.2℃,最优逼近估算在0~0.1℃。一年当中,最优逼近以3—10月的估算情况好,7月符合次数最多(图 2b),冬半年较少,与文中近10年序列的检验结果相似,即温度较高时湿球温度的符合情况好,温度较低时符合相对较弱。牛顿迭代法的多年符合情况则在夏半年较弱,冬半年较好,8月符合次数最少。且最优逼近法在各月与观测值相符合的次数与牛顿迭代法量级差异显著,相较而言,牛顿迭代法受序列的不均一性影响较大。可见,在长年代序列当中,最优逼近的估算结果相较于牛顿迭代更接近于观测值,稳定性好,符合率高。
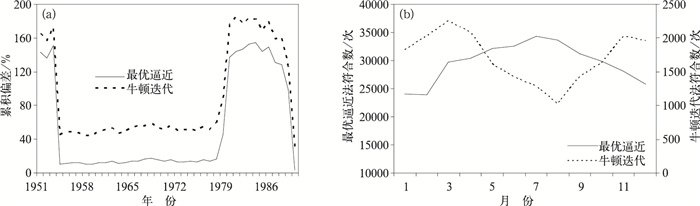
|
图 2 最优逼近、牛顿迭代估算湿球温度历年累积偏差(a)及月符合情况(b)变化曲线 Fig. 2 Variation curves of cumulative deviation (a) and monthly coincidence rate (b) of wet bulb temperature over the years between the optimal approximation and Newton iterative estimation |
从1991年至百叶箱干湿球温度表观测截止年份的检验分析可知,最优逼近法的估算精度高,离散度低,与湿球温度的观测值符合情况好,在某种程度上其计算值可以替代人工实测湿球温度; 而由长序列数据的分析发现,最优逼近法的估算结果受序列不均一性的影响较小,估算效果稳定性好,符合率高,由此可知,在一定时间尺度上,最优逼近法利用水汽压(相对湿度)、温度、气压数据对后续湿球温度进行估算是可行的。
考虑到湿球温度的观测有覆冰与否,即湿球表面存在固、液两种状态,而最优逼近法的设计中以0℃作为结冰与否的临界点,因此研究对历史数据温度在0℃以上的序列进行了偏差分析,结果表明总偏差有所减少,但减少比重较小,可见覆冰观测会带来估算的偏差,但整体影响较小。而工程设计应用中多考虑最热月的湿球温度,故覆冰观测的影响可不予考虑。
此外,文中选取百叶箱柱状干湿表仪器类型进行估算结果显示,最优逼近法与实际仪器观测值的差异亦较小,其序列值相对于原始数据序列,对于湿球温度数据的连续性研究更为可靠。
5 结论(1) 牛顿迭代、最优逼近法对江苏省湿球温度的估算相对于观测值偏大,但程度较小,远低于湿球温度的观测精度(0.1℃),效果较好。其中,以最优逼近法更接近于湿球温度的观测值,离散度低,符合率高(>90%),明显优于牛顿迭代法(12.7%~20.1%),呈现出09—20时符合率高,日出前后符合率低的日变化特征。
(2) 最优逼近法的计算结果偏差较小,稳定性好,更符合湿球温度观测值的自身特征。在由天气现象导致的水汽压突然增大情景下,最优逼近法的估算结果不受影响,效果明显好于牛顿迭代估算(偏差最大可至17.4℃)。
(3) 在长年代序列的估算中,最优逼近法的结果离散度低,更接近观测值,符合情况优于牛顿迭代,且在逐月的变化上与近10年序列检验结果相似,即温度较高时湿球温度的估算符合情况好,温度较低时符合相对较弱,稳定性好,受序列不均一性影响较小。
综合分析可知,最优逼近法利用水汽压(相对湿度)、温度、气压数据对后续湿球温度进行估算是可行的,且相对长年代数据序列的不均一性,研究采用的1991年至停止观测年份的百叶箱干、湿球温度表相关参数进行湿球温度的估算,其序列对于湿球温度整体数据连续性研究更为可靠。
李亚丽, 任芝花, 陈高峰, 等, 2015. 自动与人工观测气温差异偏大的原因及影响分析--以143个国家基准站为例[J]. 气象, 41(8): 1007-1016. DOI:10.7519/j.issn.1000-0526.2015.08.010 |
林婵, 王起峰, 朱良山, 2013. 基于LM-BP神经网络的湿球温度计算模型[J]. 水电能源科学, 31(1): 164-166. |
潘晓春, 程春龙, 2015. 大气湿球温度计算的牛顿迭代法[J]. 电力勘测设计, (3): 22-25. |
任芝花, 张志富, 孙超, 等, 2015. 全国自动气象站实时观测资料三级质量控制系统研制[J]. 气象, 41(10): 1268-1277. DOI:10.7519/j.issn.1000-0526.2015.10.010 |
荣剑文, 2008. 湿球温度的计算及应用[J]. 制冷技术, (4): 38-40. |
王瑞, 许小川, 陈钰文, 等. 2014. 江苏省湿球温度的气候特征分析//第十一届长三角气象科技发展论坛论文集, 139-139.
|
魏华兵, 郭江峰, 2011. 自动气象站湿球温度快速计算方法[J]. 气象, 37(8): 1038-1041. DOI:10.7519/j.issn.1000-0526.2011.08.017 |
赵永胜, 刘德平, 胡长权, 2009. 无资料地区湿球温度计算方法研究[J]. 电力勘测设计, (5): 32-35. |
中国气象局, 2003. 地面气象观测规范[M]. 北京: 气象出版社.
|
中国气象局. 2015. 气候可行性论证技术指南系列之工程项目采暖通风和空气调节气象参数计算.
|
中华人民共和国国家能源局, 2012. DL/T 5158-2012.电力工程气象勘测技术规程[M]. 北京: 中国计划出版社.
|
朱业玉, 陈辉, 姬兴杰, 等, 2013. 基于分段函数法计算湿球温度研究[J]. 气象与环境科学, 36(4): 6-9. |
朱艺青, 王振会, 李南, 等, 2016. 南京雷达数据的一致性分析和订正[J]. 气象学报, 74(2): 298-308. |
 2016, Vol. 42
2016, Vol. 42 
