引言

我国自2010年以来，风电装机总量持续位居世界第一，至2015年底我国风力发电累计并网装机容量达到了1.29亿kW。根据我国十三五可再生能源发展规划，到2020年，我国风电装机要达到2亿kW以上，《中国风电发展路线图 2050》(国家发展和改革委员会能源研究所，2014)，将风能太阳能资源开发利用确定为我国实现低碳能源战略的主要途径。

风电开发的首要环节是风能资源评估，风力发电机组(简称WTGS)选型参数是风能资源评估的重要内容，是风电机组选型和风电场设计的基础依据。国际电工委员会制定的《Wind turbines-Part 1:Design requirements》(以下简称IEC 61400-1)(IEC, 2005)，是风电开发领域应用最广泛的规范性文件，我国制定的相关规范(中国机械工业联合会, 2001; 北京鉴衡认证中心等, 2012)，多是在IEC规范的基本框架下转化而来。然而，随着我国大规模风电场的建设运行，尤其大量建设在复杂地形和沿海台风影响区域风电场的运行，发电企业逐步发现，很多风电场的实际发电表现和风电机组的运行稳定性与项目可研设计预期有较大偏差，一方面，风电机组抗击当地极端天气的能力不足，故障率居高不下，另一方面也存在过高估算风电机组的安全参数导致选型失误，从而造成风电场发电效益低下等。这些问题常常与项目前期风能资源测量和评估的准确性、可靠性密切相关，也与现行规范推荐的参数评估方法在不同地区的适用性以及对规范指导的技术要求执行不到位有关。

本文利用全国风能资源专业观测网测风塔观测数据，在观测数据质量检验(任芝花等, 2015)和有效完整性判别(Huang et al, 2015)条件下，选择了其中的193座测风塔实测数据，就IEC 61400-1规范推荐的风电机组选型的极值风速的估算方法与我国规范推荐的方法进行比较，分析其在我国不同地区的适用性，并对我国现行规范推荐的湍流强度特征参数的可靠性、代表性进行分析和讨论，以期对目前我国风能资源评估中存在的问题进行剖析，为推动该领域的技术发展和相关规范的修编提供思路和参考依据。

1 基础资料处理

本文采用的基础数据，是从全国风能资源专业观测网设置的400座测风塔2年多的观测资料中，选择了1年度观测数据有效完整性≥90%的193座测风塔观测数据。

全国风能资源专业观测网的400座测风塔中，70 m塔329座、100 m塔68座、120 m塔3座，均为正三角形桅杆式钢结构拉线塔，风速观测高度设置在离地面10、30、50、70、100、120 m高度层。测风仪采用华云公司生产CAWS1000-GSW型以及无锡公司生产的ZQZ-NT型测风系统，两类风速传感器启动风速≤0.5 m·s^-1，测量范围为0~75 m·s^-1，风速采样频率为1 s，数据采集器记录逐个10 min的平均风速、3 s极大风速以及风速标准差。

考虑目前大型WTGS轮毂高度多在70 m左右，因此以各塔70 m高度层连续12个月(1个年度)的逐10 min平均风速观测资料为分析目标。由于外场观测过程中常受到恶劣天气和环境因素的影响而导致观测数据异常或缺测，参照相关规范(中国水利水电建设工程咨询公司，2002；中国气象局, 2007)对原始观测数据进行质量检验，并计算其数据有效完整率：

$ \begin{array}{l} 数据有效完整率 = \\ \;\;\;\frac{{应测数据量 - 缺测数据量 - 无效数据量}}{{应测数据量}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \times 100\% \end{array} $

(1)

式中的数据量是指全年逐个10 min平均风速记录个数。

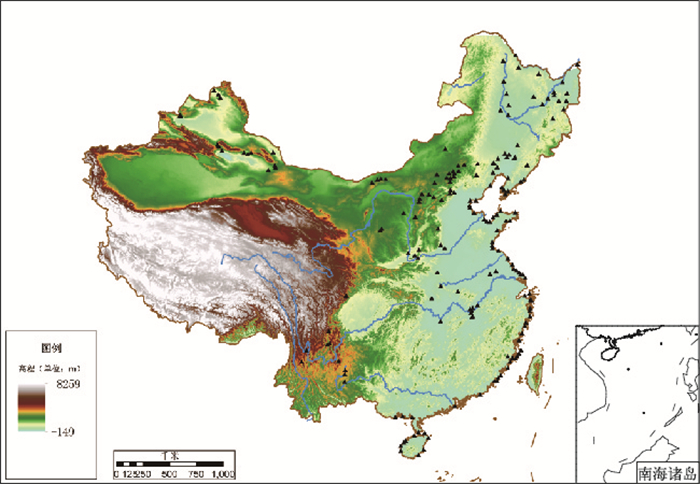
从400座测风塔观测资料中，选取了处于不同地形地貌上，并且满足一个年度内测风塔70 m高度获取的风速观测数据有效完整率≥90%的193座测风塔观测数据，其中，70 m高度的测风塔有160座、100 m高度的测风塔有30座，193座测风塔的地理位置分布见图 1。

2 极值风速分析

IEC 61400-1和我国规范《风力发电机组设计要求》(中华人民共和国质量监督检验检疫总局 & 中国国家标准化管理委员会, GB/T18451.1-2012) 均以极值风速作为风电机组安全等级的分级指标(见表 1)。这里的极值风速V_ref是指WTGS轮毂高度上50年一遇的10 min平均最大风速。

表 1中，V_ref为WTGS的分级参考风速，以50年一遇10 min平均最大风速来确定。

2.1 极值风速估算方法

(1) IEC规范推荐的极值风速计算方法

IEC 61400-1中给出的极值风速模型为：

$ {V_{50}}\left(z \right) = {V_{{\rm{ref}}}}{(z/{z_{{\rm{hub}}}})^{0.11}} $

(2)

式中，V₅₀(z)为高度z处的50年一遇10 min平均最大风速，V_ref为WTGS的分级参考风速(表 1)，z_hub为轮毂高度。当z等于z_hub，那么，式(2) 就可改写为：

$ {V_{50}}\left({{z_{{\rm{hub}}}}} \right) = {V_{{\rm{ref}}}} $

(3)

IEC 61400-1定义在标准的风力机等级中，有以下经验表达式：

$ {V_{{\rm{ave}}}} = 0.2{V_{{\rm{ref}}}} $

(4)

式中V_ave为年平均风速。

由式(3) 和式(4)，轮毂高度处50年一遇10 min平均最大风速表达式写为：

$ {V_{50}}\left({{z_{{\rm{hub}}}}} \right) = 5{\rm{ \times }}{V_{{\rm{ave}}}} $

(5)

式(5) 表明，WTGS轮毂高度z_hub的50年一遇10 min平均最大风速，可以通过轮毂高度年平均风速V_ave的5倍来估算，这种方法简便、易行，因此，目前的很多风电场风资源评估，只采用风电场测风塔获取的1年度风速平均值，就可以通过式(5) 估算出项目的极值风速参数。

(2) 我国规范推荐的极值风速计算方法

世界上许多国家和地区在工程结构抗风的相关规范多推荐采用极值Ⅰ型分布函数来估算多年一遇的重现期风速(中华人民共和国住房和城乡建设部，2012；中华人民共和国建设部, 2007；ASCE, 2006; Architectural Institute of Japan, 2004; Building Department of Hong Kong, 2004; Ge et al, 2010)，为规范和指导我国风能资源评价工作，国家发改委于2004年发布了《全国风能资源评价技术规定》(国家发展和改革委员会，2004)，该技术规定沿用了其他工程结构的抗风规范，推荐以极值Ⅰ型分布函数推算风电场50年一遇10 min平均最大风速。

极值Ⅰ型分布函数为：

$ F\left(x \right) = {\rm{exp}}\{ - {\rm{exp}}\left[ { - \alpha \left({x - u} \right)} \right]\} $

(6)

式中，u为分布的位置参数，即分布的众值，α为分布的尺度参数。

黄浩辉等(2007)从多个大型工程重现期风速计算实践中发现对极值Ⅰ型分布函数中的参数估算时，选择不同的方法会产生较大的差异，尤其对更长重现期的风速计算结果影响更为明显，为此，不少学者(黄浩辉等，2007；孟庆珍等，2001；段忠东等，2004)对极值Ⅰ型分布函数中参数估算的3种常用方法——矩法、耿贝尔法和极大似然法等进行对比研究，发现大多数情况下采用耿贝尔法拟合效果最好。采用耿贝尔法对参数α和μ进行估计，如下式：

$ \alpha = \frac{{{c_1}}}{\sigma } $

(7)

$ u = \mu - \frac{{{c_2}}}{\alpha } $

(8)

式中，μ和σ分别为参证站10 m高度逐年最大风速序列样本的平均值和标准偏差，计算公式见式(9) 和式(10)，c₁、c₂为与样本数量有关的参数，多部规范中直接给出了参考取值(中华人民共和国住房和城乡建设部，2012)，见表 2。

$ \mu = \frac{1}{n}\sum\limits_{i = 1}^n {{V_i}} $

(9)

$ \sigma = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {\left({{V_i} - \mu } \right)} } $

(10)

式中，n为风速样本数，V_i为逐年风速最大值样本。

则z_s10高度处(对国家气象站，z_s10为10 m左右)50年一遇10 min平均最大风速按下式计算：

$ {V_{50}}({z_{s10}}) = u - \frac{1}{\alpha }{\rm{ln}}[{\rm{ln}}\left({\frac{1}{{50 - 1}}} \right)] $

(11)

式中，z_s10代表参证站测风仪所在的10 m高度，V₅₀(z_s10)参证站10 m高度50年一遇10 min平均最大风速。

利用式(11) 中进行某地的多年一遇的重现期风速计算，u的取样为该地逐年最大风速序列，基础数据序列长度通常要求不少于30年。由于风电场短期测风塔的逐年最大风速序列长度难以满足极值Ⅰ型分布函数拟合所需要的序列长度要求，因此，需要引入与观测塔相关性较高的长期气象站历史测风数据。《风电场风能资源评估方法GB/T 18710-2002》(中国水利水电建设咨询公司，2002)和《风电场气象观测及资料审核、订正技术规范QX/T74-2007》(中国气象局，2007)均推荐了建立两地风速订正关系的技术方法，其中，GB/T 18710-2002推荐采用分风速方位的线性回归法，QXT74-2007推荐了基于大风特性的风速比值法，两种方法均有广泛的应用。不少学者对风电场测风塔短期测风数据与周边长期气象站同步测风的相关性分析的样本选择进行了研究(杨梦兮等，2014；谌玲等，2014)，采用日最大风速建立的相关关系比采用全部测风数据建立的相关关系，推算的50年一遇10 min平均最大风速结果更为稳定。

《全国风能资源详查和评价报告》(宋丽莉等，2014)在参证气象站比选、长期气象站最大风速序列一致性检验处理、测风塔与参证气象站同步测风数据相关分析等方面，做了细致严谨的分析研究，在大量试验研究基础上，采用计算水文不同重现期极值常常使用的极值Ⅰ型分布函数(李兰等，2013；郭渠等，2015)并以耿贝尔法进行其中的参数估算，以日最大风速样本的相关关系作为测风塔和长期气象站处重现期风速计算的修正依据，从而给出了全国风能资源专业观测网396座测风塔70 m高度上50年一遇10 min平均最大风速。本文直接引用了《全国风能资源详查和评价报告》对193座测风塔70 m高度层的50年一遇10 min平均最大风速计算结果。

2.2 两种方法的计算结果差异分析

采用IEC 61400-1推荐的方法，通过式(5) 计算193座塔70 m高度上的50年一遇10 min平均最大风速，以V_{50_1}表示，《全国风能资源详查和评价报告》给出的这一参数，以V_{50_2}表示，计算相对偏差(RD)，表达式为：

$ RD = \frac{{{V_{50\_1}} - {V_{50\_2}}}}{{{V_{50\_2}}}} \times 100\% $

(12)

表 3显示了两种方法计算结果的相对偏差特征。可以发现：两种方法计算结果十分相近的有7座测风塔，相对偏差在±1%范围内(占总塔座数的4%)，两种方法计算结果比较接近的有42座塔，相对偏差在±5%范围内(占总塔座数的21%)；总体来看，采用IEC推荐的式(5) 估算的极值风速比采用极值Ⅰ型估算法得到的结果偏小的测风塔占了多数，193座测风塔中，IEC计算值偏小10%以上的有121座塔，偏小达到30%以上的，有44座测风塔，有4座测风塔偏小50%以上，其中位于浙江温州的一座测风塔，若按照IEC估算法计算的50年一遇10 min平均最大风速为22.5 m·s^-1，而采用极值Ⅰ型函数估算结果为54.6 m·s^-1，偏小了32.1 m·s^-1；IEC估算值为正偏差的比例较小，193座塔中，正偏差达10%以上的只有9座测风塔，最大正偏差为26%，出现在新疆达坂城，IEC估算法计算的50年一遇10 min平均最大风速为51.0 m·s^-1，极值Ⅰ型函数估算结果为40.4 m·s^-1，偏大了10.6 m·s^-1。

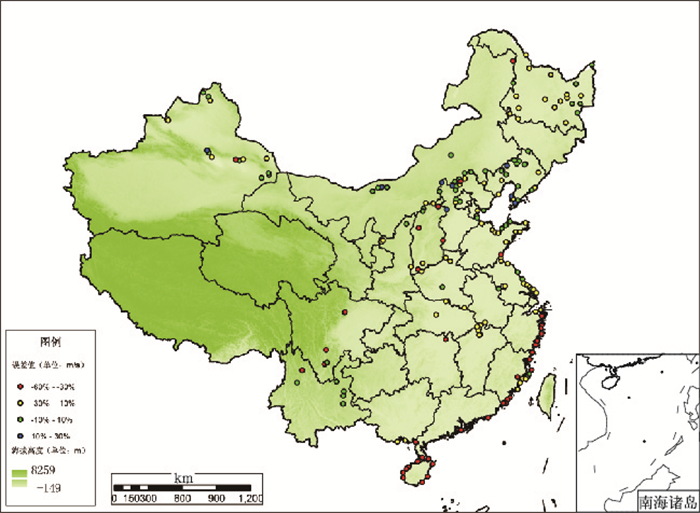
图 2给出了以两种方法计算的193座测风塔处极值风速的偏差分布图，可以看出，负偏差超过-30%以上的测风塔(图中红色圆点，占比23%)，集中分布在我国长江口以南的东南沿海地区，这一地区的极值风速多由热带气旋天气所致，过低地估算极值风速，将给风电场带来极大的安全隐患；两者偏差较小的测风塔主要分布在西北和华北地区的开阔平缓地形区域，但同时正偏差达10%以上的测风塔也分布在这一地区，因此，这些地区同时存在着安全和效益的矛盾。

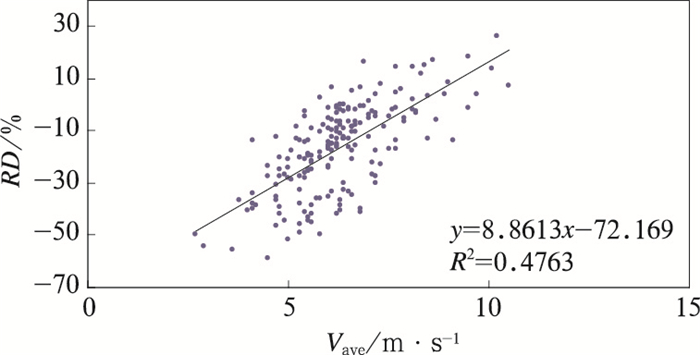
由式(5) 可见，极值风速主要依赖年平均风速，那么，相对偏差(RD)与年平均风速(V_ave)也会存在相关性，从图 3给出的RD与V_ave相关散点图来看，随着V_ave的增大，RD由显著的负偏差逐步演变为正偏差，但RD由负到正的演变伴随V_ave的变化幅度可从6~10 m·s^-1，这一现象说明了我国不同地区的极值风速的复杂性，以IEC推荐的年平均风速的5倍参数进行估算，可导致我国很多地区、特别是我国东南沿海地区风电场存在极大的安全隐患，同时，部分地区因过高估算极值风速，从而导致不必要的投资浪费和发电效益的降低。

3 湍流强度特征值分析 3.1 湍流强度特征值评估方法

湍流强度(turbulence intensity，简写为I)，表示瞬时风速偏离平均风速的程度，是评价气流稳定程度的指标(盛裴轩等，2003)，以下式表达：

$ I = \frac{\sigma }{V} $

(13)

式中，σ为风速标准差，指阵风(一般为1~3 s时距)风速相对平均(一般为10 min时距)风速的标准偏差，V为10 min平均风速。

湍流强度直接影响到风电机组的疲劳载荷，是导致WTGS故障甚至损毁的关键因素之一。实测和仿真试验均证实了相同风速下风电机组的疲劳等效载荷随着湍流强度的增加而增大(付德义等，2015)，风电机组的气动性能和最大功率系数均显著降低(祝魁等，2012)。为此，IEC 61400-1规定了针对WTGS抗御湍流影响的安全等级分级，分为4类(表 4)，我国相关规范(中华人民共和国质量监督检验检疫总局&中国国家标准化管理委员会, GB/T18451.1-2012) 也直接引用了这一特征参数。

表 4中，I_ref为不同WTGS等级湍流强度参考值，是WTGS轮毂高度处风速15 m·s^-1时的湍流强度特征参考值。规范规定，WTGS轮毂高度处15 m·s^-1风速时的实际湍流强度应I₁₅≤I_ref。

目前，我国相当一部分风能资源评估报告简单地将轮毂高度处风速15 m·s^-1的平均湍流强度I₁₅误认为就是WTGS分级的标准(王承凯，2009)，对I₁₅的计算表达式为：

$ {I_{15}} = \frac{1}{n}\sum\limits_{i = 1}^n {{I_{15, j}}} $

(14)

式中，I_15，j为14.6~15.5 m·s^-1风速范围内第j个风速样本的湍流强度值，n为风速样本数。

按照IEC 61400-1等规范的解释，确定WTGS等级选取的湍流强度指标，应以15 m·s^-1风速段的所有风速样本湍流强度I_15，j的90%分位数处的值为指标，具体做法是：将I_15，j按照数值大小排序，取该序列从小到大的90%分位数处的值做为WTGS等级选取的湍流强度指标，在此记为I_15，90%。按照IEC规范要求的正确的做法是，以I_15，90%与表 4中的I_ref对应在正常湍流模型(NTM)中的值比较，最终确定WTGS等级的选取。

IEC61400-1还进一步给出了用于对确定等级WTGS的湍流安全性评估的正常湍流模型，表达式为：

$ TI = \frac{{{\sigma _1}}}{{{V_{{\rm{hub}}}}}} $

(15)

式中，V_hub为风电机组轮毂高度处的发电风速特征风速，通常选取≥风机额定风速的0.2倍的风速样本；TI、σ₁分别为风机发电风速段各特征风速的湍流强度值和标准差，IEC还给出了σ₁的经验公式：

$ {\sigma _1} = {I_{{\rm{ref}}}}(0.75{V_{{\rm{hub}}}} + b) $

(16)

并推荐式(16) 中，b=5.6 m·s^-1。

将式(16) 带入式(15) 中，可以得到正常湍流模型的表达式：

$ TI = \frac{{{\sigma _1}}}{{{V_{{\rm{hub}}}}}} = 0.75{I_{{\rm{ref}}}} + \frac{{5.6{I_{{\rm{ref}}}}}}{{{V_{{\rm{hub}}}}}} $

(17)

将表 4中各WTGS等级的I_ref带入式(17)，可得到IEC 61400-1定义的正常湍流模型(NTM)的A、B、C三种等级湍流强度随风速变化的参考曲线(图 4)。

实际上，以风电场建设前期的测风塔数据计算的湍流强度只为环境湍流强度，尚未考虑风电机组尾流相互影响产生的扰动而导致的湍流强度变化，与风电机组所承受的实际湍流强度还是有所差异的，在此采用193座测风塔的湍流强度参数分析结果，仍属于环境湍流强度。

3.2 湍流强度特征参数分析

以式(14) 计算出193座测风塔的I₁₅，参考表 4的I_ref等级标准，判别193座测风塔中有6%的测风塔(11座塔)为A类，13%的测风塔(25座塔)为B类，77%的测风塔(149座塔)为C类，还有4%(8座)的测风塔TI₁₅值大于0.16，属于S类，见表 5。

按照规范规定的以I_{15, 90%}作为WTGS等级确定的指标，参考表 4的I_ref等级分类标准，判别193座测风塔中有10%的测风塔(19座塔)为A类，25%的测风塔(48座塔)为B类，51%的测风塔(99座塔)为C类，有15%(29座)的测风塔I₁₅值大于0.16，属于S类(表 5)。

以I_{15, 90%}与I₁₅的WTGS等级选择结果比较，达到A、B、S类等高湍流型的测风塔明显增多了，特别是达到S类的测风塔，由8座增加到29座；达到C类的低湍流型测风塔数量由149座减少为99座。

利用IEC 61400-1正常湍流模型(NTM)，对以I_{15, 90%}与I₅₀为指标确定的WTGS等级结果进行湍流强度安全性评估。选取目前主流大型风机发电的特征风速段5~25 m·s^-1，计算193座塔70 m高度层5~25 m·s^-1风速区间的逐个10 min风速样本的湍流强度，以TI_i表示。统计结果显示，若以I₁₅的为指标确定的WTGS等级，193座测风塔中，有46座塔在5~25 m·s^-1特征风速区间的湍流强度TI_i超越了选定等级WTGS参考曲线的样本比例达到10%以上，从而，可能存在较大的安全风险；而以I_{15, 90%}指标来确定的WTGS等级，仅有15座测风塔不满足选定等级WTGS参考曲线的规范要求，需要进行进一步分析。由此可见，以I_{15, 90%}为指标确定的WTGS等级，可以更好地满足正常湍流模型对WTGS安全性评估的要求。

图 5进一步给出了以I₁₅确定的WTGS湍流强度等级分别为A、B、C类(分别标记为1#、2#、3#、4#、5#、6#塔)，但不满足正常湍流模型(NTM)的6座测风塔计算实例(见表 6)。

表 6给出了6座典型测风塔以I₁₅与I_{15, 90%}的WTGS等级选择结果。可以看出，以I₁₅确定的WTGS湍流强度等级要比以I_{15, 90%}确定的WTGS湍流强度等级低1~2个等级，说明以I₁₅确定的WTGS湍流强度等级偏低，存在较大的安全风险。

图 5显示了6座测风塔湍流强度特征参数在5~25 m·s^-1范围的变化特征。图 5a，5b，5c，5d，5e和5f是以风速在5~25 m·s^-1范围内的逐个10 min样本的湍流强度值随风速的变化，图中曲线是以I₁₅为指标确定的WTGS等级参考曲线；图 5A，5B，5C，5D，5E和5F中，三角符号是以1 m·s^-1间隔的每个风速区间的所有风速样本的湍流强度在90%分位数对应的湍流强度值(以I_90%表示，I_90%在15 m·s^-1风速区间对应值即为I_{15, 90%})，实心圆圈符号以I₁₅代入式(17) 的计算结果，以TI₁₅表示，图中实线为以I₁₅确定的WTGS湍流强度等级曲线。

从图 5A~5F可以看出，在5~25 m·s^-1，6座塔的I_90%值，几乎均超出I₁₅选定的WTGS等级参考曲线，不同风速区间I_90%值相对I_{15, 90%}选定的WTGS等级参考曲线的位置也不尽相同。如图 5E中，以I_{15, 90%}选定的WTGS等级为A类，在8~17、19、21 m·s^-1的I_90%值均在A类参考曲线以内，但在5~7、18、20 m·s^-1的I_90%值均在B类参考曲线以内，然而15 m·s^-1以上的风速样本明显较少，计算得到的I_90%值可能不具有较好的代表性，在实际WTGS选型时，应根据实际需要，综合考虑上述特征。

从以上的分析结果可以看出，目前我国风电场风能资源评估普遍采用的WTGS轮毂高度15 m·s^-1风速区间所有风速样本的湍流强度算术平均值I₁₅来确定的WTGS湍流强度等级，存在很大的不确定性，极有可能导致WTGS选型的误判，使风电机组偏于不安全，应按照IEC 61400-1的要求，以15 m·s^-1风速段的所有风速样本湍流强度的90%分位数I_{15, 90%}为指标，来确定WTGS等级的选取，再进一步根据IEC 61400-1正常湍流模型(NTM)，对确定的WTGS等级结果进行湍流强度安全性评估。

4 结论和讨论

利用全国风能资源专业观测网的193座测风塔观测数据，对IEC推荐的极端风速计算方法与我国规范推荐的基于极值Ⅰ型概率分布方法进行比较，并以目前行业领域普遍采用的以15 m·s^-1风速的平均湍流强度作为风电机组选型指标的不确定性进行分析，初步得出以下结论：

(1) 按照IEC推荐的极端风速计算方法与基于极值Ⅰ型概率分布方法计算得到全国193塔50年一遇10 min平均最大风速，发现两种方法计算结果十分相近的仅有7座测风塔，相对偏差在±1%范围内，比较接近的有42座塔，相对偏差在±5%范围内；总体来看，IEC推荐方法的计算结果多数偏小，其中偏小10%以上的测风塔有121座，偏小30%以上的有44座测风塔，而偏大10%以上的只有9座测风塔，负偏差最大值为-59%，位于浙江温州，IEC推荐方法计算结果为22.5 m·s^-1，极值Ⅰ型方法计算结果为54.6 m·s^-1，前者偏小了32.1 m·s^-1；正偏差达10%以上的只有9座测风塔，最大正偏差为26%，出现在新疆达坂城，IEC推荐方法计算结果为51.0 m·s^-1，极值Ⅰ型方法估算结果为40.4 m·s^-1，前者偏大了10.6 m·s^-1。

(2) 负偏差超过-30%以上的测风塔，集中分布在我国长江口以南的东南沿海地区，这一地区的极值风速多由热带气旋天气所致，过低地估算极值风速，将给风电场带来极大的安全隐患；两者偏差较小的测风塔主要分布在西北和华北地区的开阔平缓地形区域，但同时正偏差达10%以上的测风塔也分布在这一地区，因此，这些地区同时存在着安全和效益的矛盾。

(3) 随着年平均风速的增大，相对偏差由显著的负偏差逐步演变为正偏差，但相对偏差由负到正的演变伴随年平均风速的变化幅度可从6~10 m·s^-1，这一现象说明了我国不同地区的极值风速的复杂性，以IEC推荐的年平均风速的5倍参数进行估算，可导致我国很多地区、特别是我国东南沿海地区风电场存在极大的安全隐患，同时，部分地区因过高估算极值风速，从而导致不必要的投资浪费和发电效益的降低。

(4) 与严格按照规范，以15 m·s^-1风速段所有样本湍流强度的90%分位数处的值作为指标进行风电机组等级确定相比较，以目前行业领域普遍采用的以WTGS轮毂高度15 m·s^-1风速区间所有风速样本的湍流强度算术平均值作为指标来确定的WTGS湍流强度等级，发现193座塔中有46座塔的选型是不安全的，甚至相差2个等级。

本文所采用的全国风能资源专业观测网中的193座测风塔数据计算的湍流强度只为环境湍流强度，尚未考虑风电机组尾流相互影响产生的扰动而导致的湍流强度变化，在下一步的工作中，将考虑采用计算流体力学(computational fluid dynamics, CFD)模型对风电场风机尾流进行模拟分析，以考虑了风机尾流和环境湍流强度的实际湍流强度数据，对本文研究结论进行验证和补充。