引言

预报员怎样与数值天气预报指南产品相互融合，并将各自价值发挥到极致，从而使两者“合力”做出的预报预警信息有“1+1>2”的效果，是学术界及各预报中心的最新关注焦点。在2015年召开的国际数值天气预报会议上，“预报员DA”的理念被低调提出(张永，2015)。“预报员DA”借助了DA理念，将预报员的预报经验，对一些天气过程中数值天气预报(numerical weather prediction, NWP)模式容易出现的“偏激”错误进行把握。此类将预报员能力与数值预报定量信息有机结合的理念或将成为预报员与预报模式长期共处的新机制。本研究的内容——人工订正位涡改进模式预报技术便是一种典型意义上的预报员DA技术。该方法的核心特点是利用等位涡面与卫星水汽图像的对应关系及位涡的可反演性将预报员的观测和长期经验快速、合理、有效地融入到模式分析场，实现预报员主观定性的预报能力同NWP的客观定量的特点进行有机的结合，从而实现提升模式预报性能。作为对NWP预报性能的有效订正和补充，该方法既充分发挥了预报员在实时预报中的不可替代的作用，又规避了NWP模式出现的“偏激”错误，十分有助于未来天气预报服务的定量化展开。

卫星水汽观测图像的观测原理决定了其可代表高层大气的运动状况，水汽图像所看到绝大部分重要结构与导致垂直运行和气流变形场的大尺度天气过程有关系。将水汽图像应用于天气尺度诊断分析的基础便是干区和湿区以及它们的边界。这些关键特征经常和重要的高空气流相关联，例如对流层顶动力异常，即位涡的入侵等过程。在热带气旋以外的气旋性环流场中，位涡场和卫星水汽图像之间有着很好的对应关系(吴君等，2007；任素玲等，2014)。借助分析1.5 PVU或者2.0 PVU等位涡面的高度，可以较好地反映动力对流层顶的演变从而描绘位涡异常的主要特征。将水汽图像上的暗区位置与位涡分布进行比较，确定水汽图像中的暗区和模式输出中位涡异常区(对流层顶动力异常区域)之间是否匹配，可以检验模式对于天气尺度系统的预报强弱位置等特征；而将水汽图像上亮区位涡分布进行比较可以确定在急流的湿侧，动力对流层顶高的地方(等位涡面高)和水汽图像上灰度亮的地方是否匹配，从而检验模式对于活跃的斜压叶状云系统的预报情况。通过以上的对应关系，则开辟了一种全新的直观快速的定性模式检验途径，从而为下一步订正改进模式预报奠定了基础(许健民等，2008；蒋建莹等，2014；陶祖钰等，2012；赵小平等，2014; 陈秀杰等，1998)。Hoskins等(1985)从理论上全面、清晰地阐述了位涡反演理论，指出在满足一定前提条件的情况下，就能从给定的位涡质量分布反演出相应的风、压和温度场，即位涡具有可反演性。因此通过模式位涡与卫星水汽图像的对比订正模式位涡，即可实现合理改进模式温压风全部物理量场的目的，开拓了主观订正模式的新思路，目前国外这项技术也已发展得较为完善并取得较好的应用效果(Hoskins et al, 1985; Georgiev et al, 2001)。

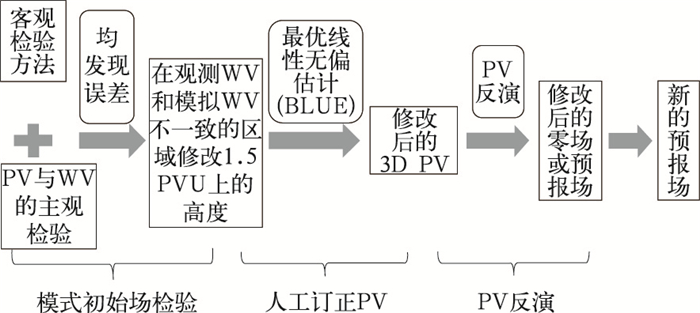
1 方法说明 1.1 人工订正位涡改进模式预报的技术流程

人工订正位涡(PV)改进模式预报的技术流程见图 1。技术流程通过客观检验方法包括要素检验，如风场、位势高度等检验或模式风场与观测风场对比, 以及PV与卫星水汽观测图像(WV)的主观对比发现模式误差后，通过PV和WV的对应关系人工修改PV，用修改后的PV场进行位涡反演并重新计算以得到新的预报，从而达到改进模式初始场的效果。

为实现以上修改位涡高度并通过位涡反演得到风场和温度场，就要涉及到两大处理步骤：

① 如何使调整后的位涡较合理地融合入三维初始场。

② 对调整后的位涡进行位涡反演。

为了满足未来业务中人工修改位涡分布的合理性和交互便捷性的要求，采用最优线性无偏估计(BLUE)方法进行处理(Partick et al，2007; Arbogast et al, 2012)。其具有计算量小，运算速度快又兼顾合理性的特征。该方法结合了历史数据将人工订正的位涡合理地覆盖整个模式气柱，相较于常规插值，BLUE方法结合了模式历史物理量场统计特征，使得修改量更合理有效地融入模式场。具体方法如下：

(1) 预报员修改1.5 PVU上的高度。

该高度并不一定发生在标准模式垂直层次上，如发生在300~200 hPa，相应的200和300 hPa会产生同样的，表示根据线性关系插值求得更改高度上的PV，其中PV_{closest level above}和PV_{closest level below}分别表示距离1.5 PVU高度最近的上下两个模式面的PV。

(2) 为保证PV垂直梯度不变，对改变高度的上下各4层采用同样的ΔPV。

$ \begin{array}{l} \Delta PV = 1.5{\rm{PVU}} - \\ \;\;\;\;\;\;\;\;\;\;f\left({PV, P{V_{{\rm{closest level above}}}}, P{V_{{\rm{closest level below}}}}} \right) \end{array} $

(1)

(3) 通过最优线性无偏估计(BLUE)方法将PV订正信息插值到模式各层次上。其中，改变的8层作为观测矢量，原始模式场作为背景场，则订正后的PV场可写为：

$ {P_{{\rm{new}}}} = {P_{{\rm{old}}}} + \boldsymbol{B}{\boldsymbol{H}^{\rm{T}}}{(\boldsymbol{HB}{\boldsymbol{H}^{\rm{T}}} + \boldsymbol{R})^{ - 1}}\Delta P $

(2)

式中，R为观测误差矩阵，B为背景误差协方差矩阵，为8个PV订正矢量。采用1个月的数据作为样本计算B，H为观测算子。假设R值小可忽略，则

$ {P_{{\rm{new}}}} = {P_{{\rm{old}}}} + \boldsymbol{B}{\boldsymbol{H}^{\rm{T}}}{(\boldsymbol{HB}{\boldsymbol{H}^{\rm{T}}})^{ - 1}}\Delta P $

(3)

由以上计算得到了预报员主观订正后的位涡场。

采用了分部式位涡反演方法对预报员主观订正后的位涡场进行反演，从而得到相应的温压风场。

1.2 位涡反演方法

目前常用的位涡反演方法主要是具有圆形轴对称结构的孤立位涡反演、准地转位涡反演和分部(片)位涡反演(piecewise PV inversion, PPVI)三种，在上述介绍的三种反演方法中，具有圆形轴对称结构的孤立位涡反演倾向于理论研究，而准地转位涡反演是线性的，对于实际的大气运动过程，分部(片)位涡反演PPVI方法(Arbogast et al, 2008; Davis, 1992a; 1992b;Davis et al, 1991; Wang et al, 2003; Charney, 1995; 寿绍文, 2010)不仅可以较合理地反演位涡，还能定量分析各种物理过程对大气运动的影响，有助于认识大气运动规律。因此研究采用的位涡反演方法是分部(片)位涡反演方法，具体方法参照了Davis等(1991)和Wang等(2003)所述的反演原理。

下面以球坐标系中的大尺度运动说明分部(片)位涡反演的方程：对于大尺度运动，散度方程可简化为平衡方程，在球坐标系中，平衡方程可以写为：

$ {\nabla ^2}\mathit{\Phi } = \nabla \cdot\left({f\nabla \phi } \right) + \frac{2}{{{a^4}{\rm{co}}{{\rm{s}}^2}\varphi }}\frac{{\alpha (\partial \phi /\partial \lambda, \partial \phi /\partial \varphi)}}{{\partial \left({\lambda, \varphi } \right)}} $

(4)

式中，Φ为等压面位势，ϕ为流函数, φ为球坐标系纬度。

Ertel位涡在球坐标系中可近似写为：

$ \begin{array}{l} q = - \frac{{gk\pi }}{P}\left( {\eta \frac{{\partial \theta }}{{\partial \pi }} - \frac{1}{{a{\rm{cos}}\varphi }}\frac{{\partial v}}{{\partial \bar a}}\frac{{\partial \theta }}{{\partial \lambda }} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{a}\frac{{\partial u}}{{\partial \pi }}\frac{{\partial \theta }}{{\partial \varphi }}} \right) \end{array} $

(5)

式中，η为绝对涡度的垂直分量，k=R_d/c_p, π=c_p(p/p₀)^k，取静力平衡近似于水平无辐散近似则式(5) 可以改写为

$ \begin{array}{l} q = \frac{{gk\pi }}{P}\left[ {\left({f + {\nabla ^2}\phi } \right)\frac{{{\partial ^2}\mathit{\Phi }}}{{\partial {\pi ^2}}} - \frac{1}{{{a^4}{{\cos }^2}\varphi }}\frac{{{\partial ^2}\phi }}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\Phi }}}{{\partial \lambda \partial \pi }}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{a^2}}}\frac{{{\partial ^2}\phi }}{{\partial \varphi \partial \pi }}\frac{{{\partial ^2}\mathit{\Phi }}}{{\partial \varphi \partial \pi }} \end{array} $

(6)

式(4) 和式(6) 构成以位势高度和流函数为未知函数的闭合方程组，其中q作为已知函数可从式(5) 计算得到。则已知位涡q，求解诊断方程式(4) 和式(6)，可得到位势和流函数，从而得到满足平衡关系的温度场和风场。

分部反演中对于扰动量常用的是按时间或空间定义的平均和扰动，对任一瞬时变量A表示为

$ A\left({\lambda, \varphi, \pi, t} \right) = \bar A\left({\lambda, \varphi, \pi, t} \right) + A\prime \left({\lambda, \varphi, \pi, t} \right) $

(7)

式中，平均量定义为$\bar A = \frac{1}{\tau }\int_0^\tau {A{\rm{d}}t} $，其中τ表示扰动的生命周期，对于大尺度运动约为5 d左右。

变量的平均量不随时间变化，是与扰动无关的，将式(7) 代入式(4) 和式(6)，可得到位势和流函数的平均量满足的诊断方程：

$ {\nabla ^2}\mathit{\bar \Phi } = \nabla \cdot\left({f\nabla \bar \phi } \right) + \frac{2}{{{a^4}{\rm{co}}{{\rm{s}}^2}\varphi }}\frac{{\alpha (\partial \bar \phi /\partial \lambda, \partial \bar \phi /\partial \varphi)}}{{\partial \left({\lambda, \varphi } \right)}} $

(8)

$ \begin{array}{l} \bar q = \frac{{gk\pi }}{P}\left[ {\left({f + {\nabla ^2}\bar \phi } \right)\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial {\pi ^2}}} - \frac{1}{{{a^4}{{\cos }^2}\varphi }}\frac{{{\partial ^2}\bar \phi }}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial \lambda \partial \pi }}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{a^2}}}\frac{{{\partial ^2}\bar \phi }}{{\partial \varphi \partial \pi }}\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial \varphi \partial \pi }} \end{array} $

(9)

将变量的平均量和扰动量的定义式代入式(4) 和式(6)，并减去平均量方程式(8) 和式(9)，则对应的变量扰动量的方程是：

$ \begin{array}{l} {\nabla ^2}\mathit{\Phi '} = \nabla \cdot\left({f{\nabla ^*}\phi '} \right) + \frac{2}{{{a^4}{\rm{co}}{{\rm{s}}^2}\varphi }}\left[ {\frac{{{\partial ^2}\phi '}}{{\partial {\lambda ^2}}}\frac{{{\partial ^2}\phi '}}{{\partial {\varphi ^2}}} - {{\left({\frac{{{\partial ^2}\phi '}}{{\partial \lambda \partial \varphi }}} \right)}^2}} \right.+\\ \;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{\partial ^2}\bar \phi }}{{\partial {\lambda ^2}}}\frac{{{\partial ^2}\phi '}}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}\phi '}}{{\partial \varphi }}\frac{{{\partial ^2}\bar \phi }}{{\partial \varphi }} - 2\frac{{{\partial ^2}\bar \phi }}{{\partial \lambda \partial \varphi }}\frac{{{\partial ^2}\phi '}}{{\partial \lambda \partial \varphi }}} \right] \end{array} $

(10)

$ \begin{array}{*{20}{c}} {q' = \frac{{gk\pi }}{P}\left[ {\left({f + {\nabla ^2}\bar \phi } \right)\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial {\pi ^2}}} + {\nabla ^2}\phi '\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial {\pi ^2}}}} \right. + }\\ {\;{\nabla ^2}\phi '\frac{{{\partial ^2}\mathit{\Phi '}}}{{\partial {\pi ^2}}} - \frac{1}{{{a^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\left({\frac{{{\partial ^2}\phi '}}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial \lambda \partial \pi }}} \right. + }\\ {\left. {\frac{{{\partial ^2}\bar \phi }}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\Phi '}}}{{\partial \lambda \partial \pi }} + \frac{{{\partial ^2}\phi '}}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial \lambda \partial \pi }}} \right) - \frac{1}{{{a^2}}}\left({\frac{{{\partial ^2}\phi '}}{{\partial \varphi \partial \pi }}\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial \varphi \partial \pi }} + } \right.}\\ {\left. {\left. {\frac{{{\partial ^2}\bar \phi }}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\Phi '}}}{{\partial \lambda \partial \pi }} + \frac{{{\partial ^2}\phi '}}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}\mathit{\bar \Phi }}}{{\partial \lambda \partial \pi }}} \right)} \right]} \end{array} $

(11)

以上就是扰动位涡、扰动位势和扰动流函数所满足的诊断方程。按实际分析的需求，需进一步导出不同动力过程所满足的方程。设q′为总位涡扰动，q_n为某一动力过程相对应的位涡扰动，且有$q' = \sum\limits_{n = 1}^N {{q_n}} $，该式对位势和流函数也成立。再引入式(12) 可以得到分属于不同动力过程的位涡、位势和流函数扰动所满足的诊断方程：

$ {\left[ {} \right]^*} + \left[ {^ - } \right] + \frac{1}{2}{\left[ {} \right]^\prime } $

(12)

$ \begin{array}{*{20}{c}} {{\nabla ^2}{\mathit{\Phi }_n} = \nabla \cdot\left({f\nabla {\phi _n}} \right) + \frac{2}{{{a^4}{\rm{co}}{{\rm{s}}^2}\varphi }} \times }\\ {\left[ {\frac{{{\partial ^2}{\phi ^*}}}{{\partial {\lambda ^2}}}\frac{{{\partial ^2}{\phi _n}}}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}{\phi ^*}}}{{\partial {\lambda ^2}}}\frac{{{\partial ^2}{\phi _n}}}{{\partial {\varphi ^2}}} - 2\frac{{{\partial ^2}{\phi ^*}}}{{\partial \lambda \partial \varphi }}\frac{{{\partial ^2}{\phi _n}}}{{\partial \lambda \partial \varphi }}} \right]} \end{array} $

(13)

$ \begin{array}{*{20}{c}} {{q_n} = \frac{{gk\pi }}{P}\left[ {\left({f + {\nabla ^2}{\phi ^*}} \right)\frac{{{\partial ^2}{\mathit{\Phi }_n}}}{{\partial {\pi ^2}}} + \frac{{{\partial ^2}{\mathit{\Phi }^*}}}{{\partial {\pi ^2}}}{\nabla ^2}{\phi _n} - } \right.}\\ {\frac{1}{{{a^2}{\rm{co}}{{\rm{s}}^2}\varphi }}\left({\frac{{{\partial ^2}{\phi ^*}}}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}{\mathit{\Phi }_n}}}{{\partial \lambda \partial \pi }} + \frac{{{\partial ^2}{\mathit{\Phi }^*}}}{{\partial \lambda \partial \pi }}\frac{{{\partial ^2}{\phi _n}}}{{\partial \lambda \partial \pi }}} \right)}-\\ {\left. {\frac{1}{{{a^2}}}\left({\frac{{{\partial ^2}{\phi ^*}}}{{\partial \varphi \partial \pi }}\frac{{{\partial ^2}{\mathit{\Phi }_n}}}{{\partial \varphi \partial \pi }} + \frac{{{\partial ^2}{\mathit{\Phi }^*}}}{{\partial \varphi \partial \pi }}\frac{{{\partial ^2}{\phi _n}}}{{\partial \varphi \partial \pi }}} \right)} \right]} \end{array} $

(14)

实际诊断过程中，分部反演方法的步骤如下：

(1) 根据式(4) 和式(6)，由q和q计算得到Φ, ϕ以及Φ^*和ϕ^*；

(2) 根据变量的平均量和扰动量定义和式(14) 计算得到Φ′, ϕ′以及Φ^*, ϕ^*；

(3) 根据分析需要划分q_n；

(4) 根据式(12) 和式(13)，由q_n反演得到Φ_n和ϕ_n，从而诊断与某一动力过程q_n相对应的扰动位势场和扰动风场。

2 人工订正位涡修改模式初始场个例实验 2.1 个例简介及偏差分析

分别选取了2014年9月2日华北暴雨过程和2016年5月21日江南大部的大暴雨过程进行了试验分析，从而展示人工订正位涡改进模式初始场技术的实际应用状况。两次试验分别使用的T639模式和GRAPES-GFS模式零场数据。

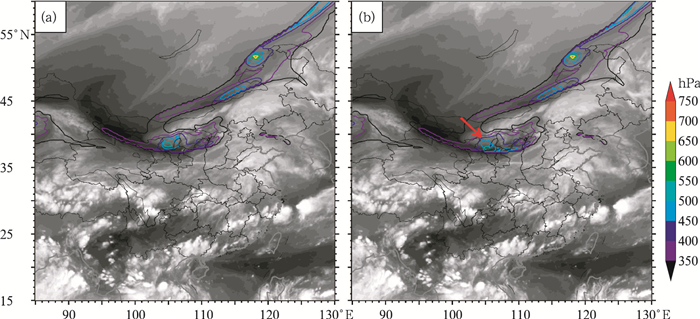
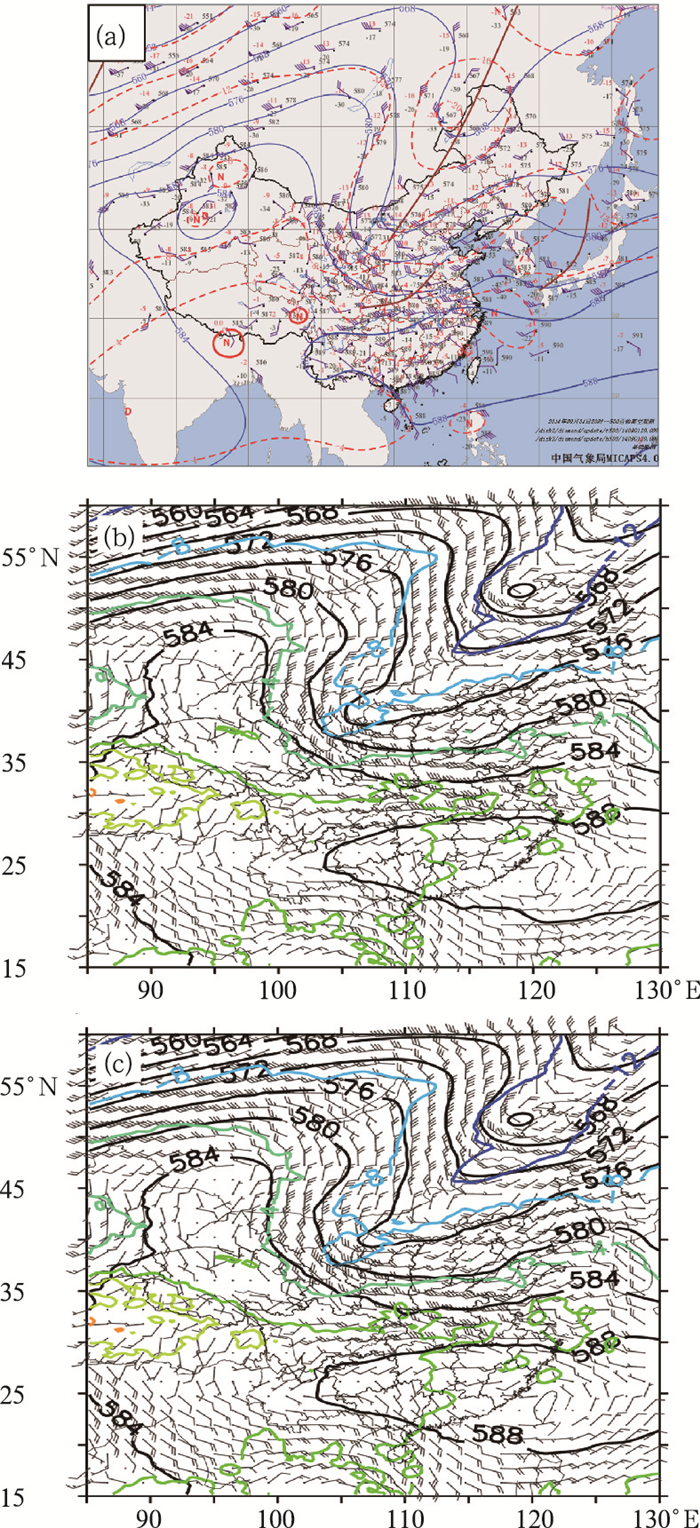
对于2014年9月2日华北暴雨过程，天气分析显示，500 hPa高空槽东移加深，低层则为低涡东移影响。从卫星水汽观测图像来看，随着高空槽的东移，槽后有较明显的弓状暗区逐渐增强东移，结合高层位涡扰动和与卫星水汽图像的对应关系，将9月1日20时T639模式零场数据分析的1.5 PVU等位涡面高度分布与同时刻卫星水汽观测进行叠加(图 2)，可见T639模式位涡下侵位置略落后于观测的卫星水汽图像暗区位置，模式较实况位置偏西偏北，对于河套西部的位涡入侵估计过强，而对于河套地区的位涡入侵强度估计偏弱。从图 3a和3b的对比来看，对于此次天气过程的关键影响系统，T639模式零场对500 hPa高空槽位置估计偏西，强度略偏强，这也映证了位涡同水汽图像暗区的对比检验结论。因此，可根据此检验结果认为T639模式9月1日20时零场天气系统位置较实况偏慢，预报员可根据此结论将位涡入侵区域向东调整，并可依据经验适当减弱河套西部地区位涡入侵的强度，增强河套地区位涡入侵强度。

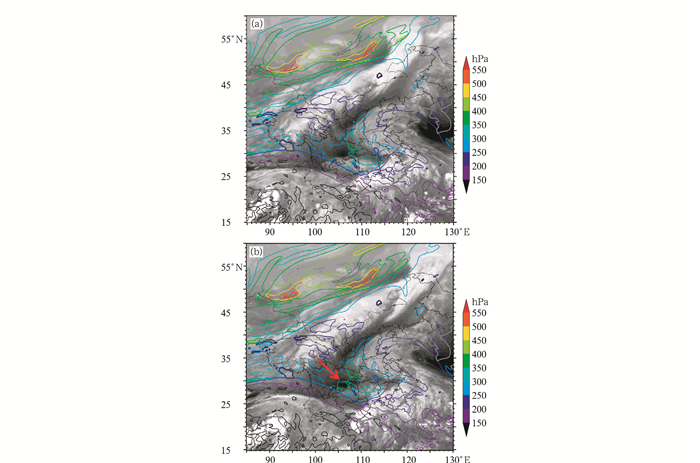
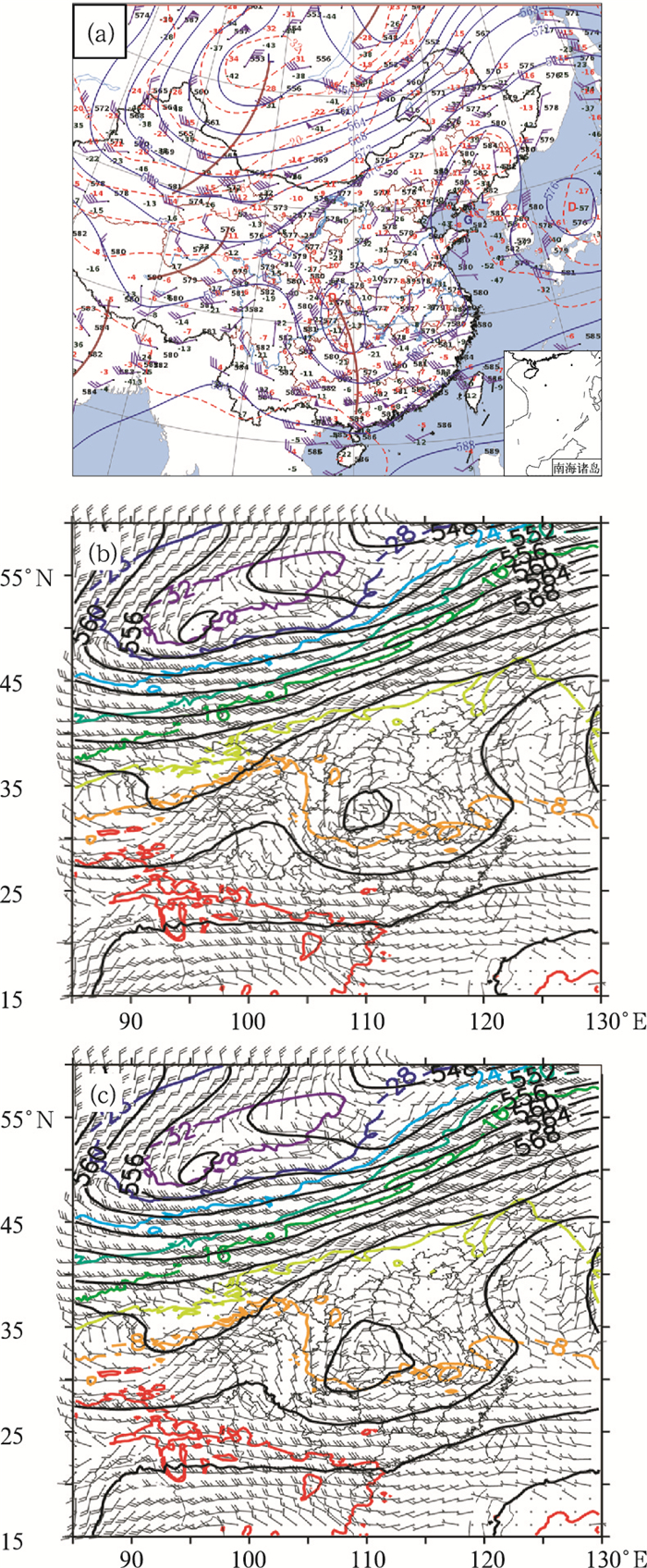
而对于2016年5月21日江南大部的暴雨过程，天气分析显示，500 hPa高原系统东移加强，并于20日08时在四川盆地东部深厚的高空涡旋系统。从卫星水汽观测图像来看，高原系统的东移，其后部有较明显的团状暗区随之显著增强，结合高层位涡扰动和与卫星水汽图像的对应关系，将5月20日08时GRAPES-GFS模式零场数据分析的1.5 PVU等位涡面高度分布与同时刻卫星水汽观测进行叠加(图 4)，可见模式位涡下侵在观测的卫星水汽图像暗区位置明显偏弱。从图 5a、5b的对比来看，对于影响此次暴雨过程的高空涡旋系统，GRAPES-GFS模式零场对500 hPa涡旋强度明显偏弱，中心位置偏北，再次映证了位涡同水汽图像暗区的对比检验方法的正确性。因此，可根据此检验结果认为GRAPES-GFS模式5月20日08时零场天气系统强度明显偏弱，位置偏北，预报员可根据此结论适当增强观测卫星水汽图像暗区的位涡入侵强度，并适当向南调整。

2.2 人工订正及结果分析 2.2.1 2014年9月2日华北暴雨过程

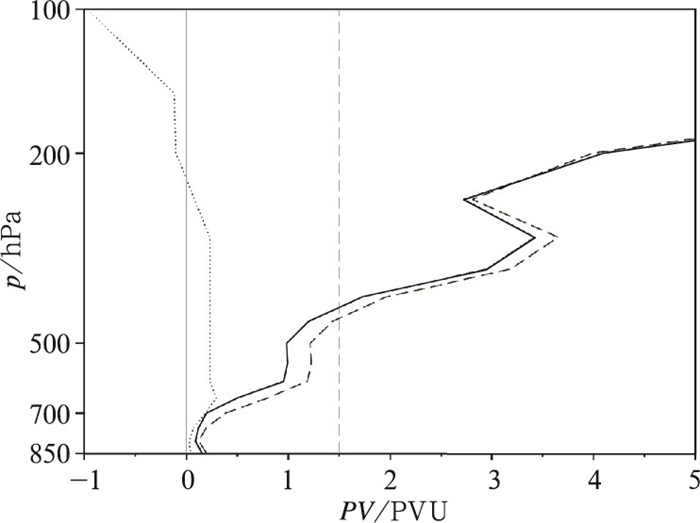
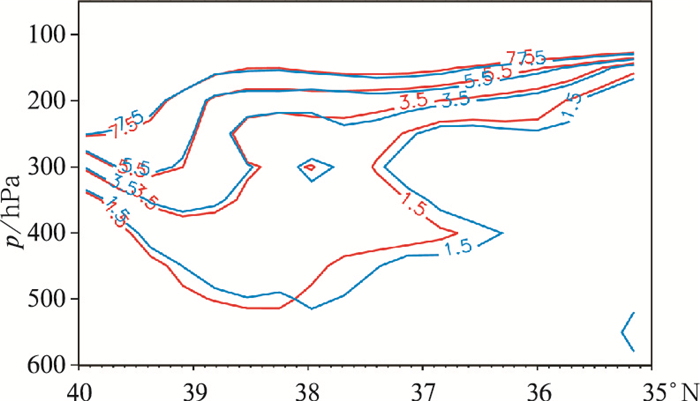
如图 2b，根据以上的检验结果，采用BLUE方法将河套西部位涡入侵强区域进行适当减弱并向南调整，再将河套地区上空的位涡入侵适当加强，整体上使得位涡入侵区域范围与实况卫星水汽图像观测暗区范围接近。另从一支气柱的位涡垂直廓线来看(图 6)，采用BLUE方法修改后的垂直廓线基本沿袭了修改前廓线的形态特征，强度整体有所增强，大气高层的位涡强度有所减弱，体现出了BLUE订正方法的合理性。沿105°E做位涡的垂直剖面可见(图 7)，采用BLUE方法修改后的位涡场分布较合理地呈现了位涡下探的形态，约38°N以北人工订正后的等位涡面整体上移，38°N以南则整体下移，同时并未出现突变的不连续面，说明人工向南订正位涡入侵区域的结果较为合理。

在确定人工订正位涡结果合理后，则可以开始利用该位涡场进行分部式位涡反演获取相应的温、压、风场。图 3是对此次天气过程的位涡反演前后的天气形势对比。

如图 3，人工订正前，我国中高纬区域呈两槽一脊形势，西北地区为一脊，5840 gpm脊点位置可达48°N以北，内蒙古中东部到河套西部地区为一槽，槽后为较强的偏北气流，中低纬度区域副热带高压较强，脊线约位于25°N左右，西脊点位于103°E左右。对比人工订正后的模式场，可以看到，在人工订正位涡位置和强度后高空形势整体出现了改变，位于河套西部地区的低槽被减弱向东调整，相应的风场有细微减弱，温度略升高。而位于我国西北地区的西风脊则有所加强，中低纬度的副热带高压则有所增强，副热带高压面积有所增大，脊线略微北抬，西脊点西进到102°E。

2.2.2 2016年3月21日江南暴雨过程

如图 4b，2.1节的云图检验结果，采用BLUE方法将四川东南部的位涡入侵区域进行适当增强并向南调整，使得位涡入侵区域范围与实况卫星水汽图像观测暗区范围接近(图 4b)，进而采用位涡反演获得人工订正后的的温、压、风、高度场。如图 5b，人工订正前，我国中高纬区域呈一槽一脊形势，西北地区为一脊，中纬度地区江南西部为一发展旺盛的闭合涡旋系统，低纬度地区5840 gpm等高线北界位于我国东南沿海一线，其外围偏西气流较为强盛。订正后的高空形势场可见，高空涡旋强度明显增强，区域范围向南拓展，涡旋外围气流较订正前明显增强，系统整体与实况更为接近。

从以上个例对比可见，分部式位涡反演方法较合理成功地反映了人工订正位涡所导致的大气系统的变化，有效订正了模式分析场的系统位置和强度，同时保证了大气环流整体的平衡性，证明人工订正位涡改进模式初始场的技术已基本实现。

3 讨论与结论

以上内容已基本实现了人工订正位涡改进模式初始场的工作，基于此，工作组将继续拓展该技术的应用与开发，如数值预报模式的云图模拟技术的应用。该技术利用数值预报模式输出的大气水凝物、辐射、风场等要素模拟出各类卫星的水汽和红外亮温图像。运用该技术，将业务数值预报模式的云图模拟图像与实时卫星观测进行对比检验，预报员不仅可非常直观地检验模式初始场天气系统位置较实况偏差，更可以直接检验得到强度的偏差，弥补了之前位涡入侵强度与水汽暗区强度只能依靠预报员经验确定对应关系的状况。进而预报员可通过修改位涡的位置和强度订正模式的初始场，并再次对此改进后的模式初始场进行云图模拟和检验至与实况接近，从而更大程度上实现改进模式预报性能的目的。

人工订正位涡改进模式初始场技术以类似于资料同化的思路将预报员的预报实践经验与数值模式预报定量特性有机地进行结合，更大限度地实现预报员和数值预报模式各自的特点能力，一定程度上突破了传统预报员的角色，更加突出了预报员天气学背景在业务工作中的不可替代性的作用。该技术在天气预报业务工作中有着较广泛的应用场景，如拓展模式检验岗位业务，每日例行检验观测云图和业务数值预报模式初始场，并做出相应判断和订正，从而改进业务数值预报模式的性能，同时为值班预报员提供模式订正建议；又如预报员可通过敏感性试验，将部分位涡异常系统人工剔除进行预报试验，进而探究天气过程的关键影响系统，为值班员提供重点关注天气系统建议等。