引言

数值模式已经成为天气预报不可替代的工具，但数值模式普遍存在误差(Bauer et al, 2015)，对数值模式的误差进行预判和订正，是数值模式应用中的主要内容(Marsh et al, 2012；李莉等，2011；于海鹏等，2014)。

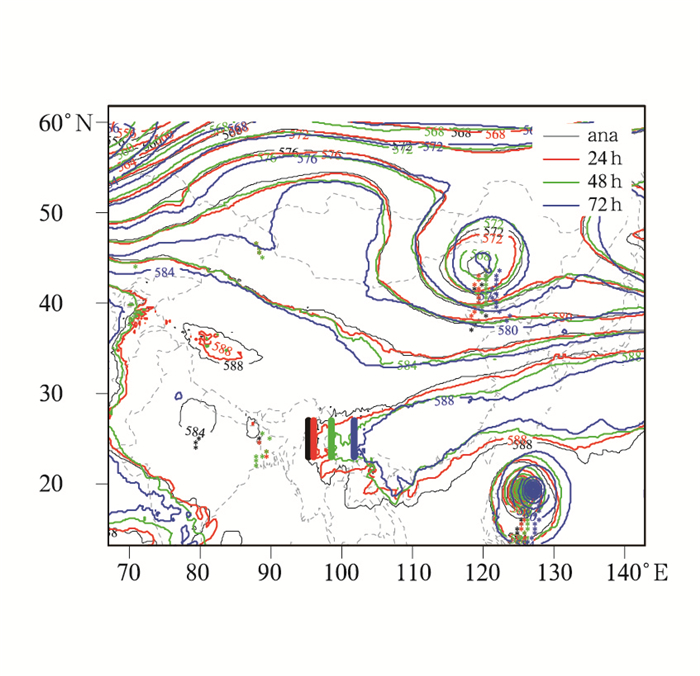
目前，在数值模式的检验订正业务和试验中，常常对比不同起报时刻对于未来同一天的预报，包括环流形势场和要素场，检验不同时效的预报之间是否一致，即预报的稳定性是否较好，另一方面，随着预报时效的临近，检验数值模式的预报是否存在一定的调整趋势(宫宇，2015；Colin，2002)。如图 1所示，对2015年8月20日08时(北京时，下同)500 hPa高度场不同时效预报的检验显示，副热带高压(以下简称副高)随时效临近，范围逐渐增大，逐渐西伸北扩，东北冷涡对应的槽线和台风天鹅的中心和对应的槽线，随时效临近，也逐渐西移，孟加拉湾附近的低涡槽线，强度预报不稳定，部分时效未达到自动识别的阈值要求。可见，副高、台风天鹅和东北冷涡均表现出较为一致的调整趋势，如果这一特征持续，则可以对未来时刻副高、东北低涡槽、台风天鹅的预报，适当往西调整，从而可以对预报进行订正。以上检验工作是基于以下两个假设：(1) 不同时效预报之间的稳定性越高，则预报的可信度越高，误差越小；(2) 预报调整趋势具有一定的持续性。

Zsoter等(2009)对比分析了欧洲中期数值预报中心(ECMWF)和英国气象局的集合预报平均值和控制预报在欧洲的稳定性特征，结果显示集合预报平均值的稳定性较控制预报更好，但不同时效预报的稳定性和预报误差之间并没有显著的关系，即稳定性较高的预报并不一定意味着预报误差也较小。Hamill(2003)运用NOAA-CIRES资料以850 hPa气温为例，对比分析了预报员常用的d(prog)/dt——预报调整趋势的有效性，结果显示不同时效的预报之间，并没有显著的预报趋势，根据“调整趋势”对预报进行订正的价值并不明显。Colin(2002)对AWIPS(Advanced Weather Interactive Processing System)中的趋势分析工具d(prog)/dt的订正效果进行了分析和检验，发现24~12 h的趋势几乎总是与更长时效的趋势相反，用趋势法对临近预报进行订正，效果不明显。

在上述工作中都证明以上两个假设不成立。但以上研究对比工作都是针对某一要素场，而对我国天气的发生发展有重要意义的天气系统，例如西北太平洋副高和西风槽等，缺乏系统性的研究对比工作。Zsoter等(2009)的研究对象为某一特定区域的500 hPa高度场，但这一研究方法并不能有效地反映出槽等重要天气系统的位置和强度变化等信息，而且只分析了预报的稳定性问题，并没有分析不同时效预报调整趋势之间的一致性和相关性大小。因此，本文针对目前业务中常用的不同时效对同一时刻预报的对比和调整趋势分析，在对副高、西风槽的位置、强度等指数定义的基础上，对EC和T639模式500 hPa西北太平洋副高和西风带以及南支槽的稳定性和调整趋势进行分析，从而研究对于重要的天气系统以上两个假设在我国是否成立，探讨模式的调整趋势是否真的能提供额外的信息。

1 资料和方法 1.1 资料

本文运用ECMWF和T639模式从2011年4月1日至2015年9月30日，每天08时和20时(北京时，下同)起报的500 hPa高度场和风场72 h时效内预报，模式输出间隔12 h，并运用双线性插值的方法将空间分辨率统一插值为0.5°×0.5°。将每年的4—9月定义为夏半年，10月至次年3月，定义为冬半年。

1.2 西北太平洋副高各指数定义

由于只研究对我国天气有影响的天气系统，本文将副高研究区域限定在10°~60°N、90°~140°E范围内，500 hPa高度场≥588 dagpm线的区域。参考各文献中的定义(伍荣生，1999；王瀛等，2007)，副高各指数定义如下：

(1) 面积指数(单位：个)：研究区域内，位势高度≥588 dagpm的网格点数；

(2) 强度指数(单位：dagpm)：研究区域内，位势高度≥588 dagpm网格点的位势高度与587 dagpm之差的和；

(3) 西脊点(单位：°)：研究区域内588 dagpm线最西位置所在的经度(图 1)；

(4) 北界指数(单位：°)：研究区域内，西脊点以东每条经线上588 dagpm高度值所达的北界纬度的平均值(图 1)。

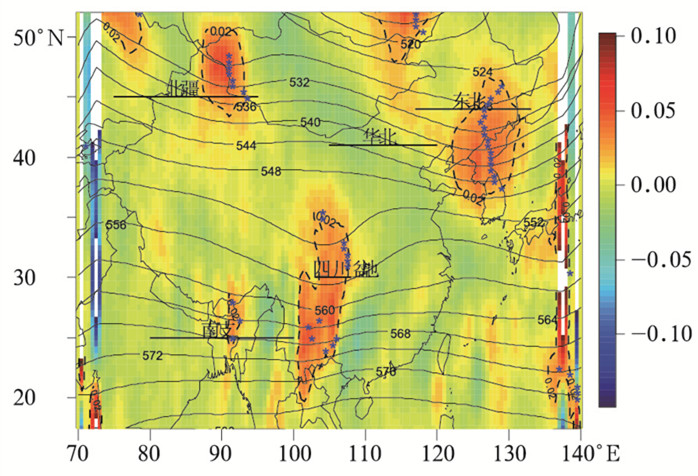
1.3 西风带槽指数定义

为了研究和定义的方便，本文只研究天气尺度及其以上的西风带槽，因此对500 hPa位势高度场进行11点滑动平均的滤波，滤除波长约为500 km以下的中尺度波动，而只保留天气尺度及其以上尺度的波动。进一步限定只研究对比西北风和西南风之间的槽，即槽区的经向风为0，槽区的正涡度值达到一定的值。根据槽的定义，并参考相关文献(胡文东等，2007；2008)，定义一个格点满足以下条件，即认为处于槽区：(a)经向风分量由北风转为了南风；(b)纬向方向为西风；(c)滤波后的高度场在纬向方向的二阶导数≥0.02，即经向风之间的涡度达到一定的值(图 2)。

为了客观分析和研究的方便，避免在自动识别时区域内同时出现两个及两个以上的槽，同时为避免在槽线南北端识别上的困难，因此将槽线识别限定在一定范围的某一纬度上。针对我国的天气气候特点，选取对我国天气具有重大影响的以下五个纬圈范围：(1)45°N、75°~95°E(新疆北部槽, BJ)；(2)41°N、105°~120°E(华北北部槽, HB)；(3)44°N、117°~133°E(东北槽, DB)；(4)30°N、103°~108°E(四川盆地槽, SC)；(5)25°N、80°~100°E(青藏高原南侧的南支槽, NZ)(图 2)。在此基础上定义槽的位置和强度指数如下：(1) 位置指数(单位：°)：槽线与识别范围内纬圈交点周围的4°范围内，满足槽区格点的平均经度。(2) 强度指数(单位：dagpm)：槽线与识别范围内纬圈交点周围的4°范围内，满足槽区格点的平均位势高度。

本文将对于同一时刻预报、以上各指数相邻24 h时效之间的差定义为调整趋势，不同时效的预报与分析场的差定义为预报误差，重点分析副高、西风带槽等天气系统随预报时效的临近，调整趋势之间是否存在显著的相关性，调整趋势是否一致。

1.4 方差分析法

分析不同时效的误差，72 h时效的预报误差为：e_72-ana=e_72-48+e_48-24+e_24-ana，则根据方差的性质(高祖新等，1998)，72 h预报误差的方差可分解为：

$ \begin{array}{l} {D_{{\rm{72 - ana}}}} = {D_{72 - 48}} + {D_{48 - 24}} + {D_{{\rm{24 - ana}}}} + 2co{v_{72 - 48, 48 - 24}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;2co{v_{{\rm{48 - 24, 24 - ana}}}} + 2co{v_{{\rm{72 - 48, 24 - ana}}}} \end{array} $

(1)

即72-48 h、48-24 h调整趋势的方差D_72-48和D_48-24、24 h预报误差的方差D_24-ana，和两倍的以上三者的两两之间协方差之和。相关系数为协方差与两个变量的标准差之商，即：${r_{x, y}} = \frac{{co{v_{x, y}}}}{{\sqrt {{D_x}} \sqrt {{D_y}} }}$。如果随时效临近，预报的调整趋势之间存在较好的一致性，那么上述三者两两之间就有较大的协方差。因此通过分析式(1) 中各项的大小，不仅能分析各项的相对大小及其对72 h预报误差的贡献，同时能分析出任意两个时效的调整趋势之间相关性的大小。

2 结果分析 2.1 西北太平洋副高的预报调整趋势

由于EC数值预报模式2011年以来进行了多次的升级(http://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-model)，在模式性能不断提高的同时，会造成模式系统偏差的改变，同时副高在冬半年和夏半年的特征不同，08和20时起报的模式性能之间可能也存在差异。为了避免以上各因素对模式趋势调整的影响，分析不同年份、不同季节、不同起报时间副高调整趋势之间的关系。

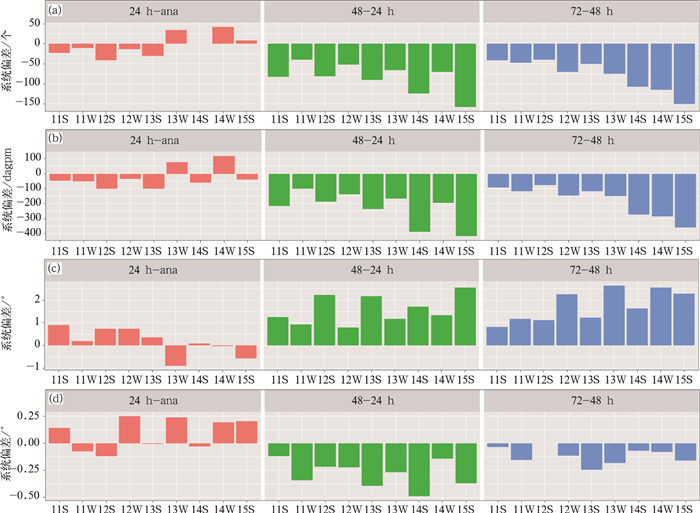
图 3所示为EC模式20时起报的副高面积指数、强度指数、西脊点和北界，不同年份不同季节，72-48 h、48-24 h和24-ana的调整趋势的平均值。副高72 h的预报较48 h的预报，不同年份不同季节，整体上面积偏小、强度偏弱、位置偏东、北界偏北，48 h较24 h的预报，以上系统性偏差更明显，24 h预报较分析场，面积指数和强度指数不同的年份和不同的季节偏差很小，且有正有负，说明无明显的系统性偏差，但副高西脊点同样存在较为明显的系统性偏东特点，副高北界存在较弱的系统性偏北特点。从图 3a、3b和3c可见，副高面积指数、强度指数和西脊点的系统性偏差，尤其是48—24 h的系统性偏差，存在较为明显的季节差异，夏半年的系统性偏差明显强于冬半年，这应该是由于副高夏半年强于冬半年所致。副高不同年份的系统性偏差并没有显著的差异，说明数值预报系统的升级、气候系统年际变率等因素，对模式调整的系统性偏差影响不明显。分析EC模式08时起报的预报，副高调整趋势的系统性偏差特征和以上20时的相似(图略)。可见，EC模式对副高72 h时效内的预报，整体上随着时效的延长，西脊点逐渐偏东，72和48 h时效预报，面积偏小、强度偏弱、北界偏南。与日常检验业务中反映现象一致(宫宇，2015)。

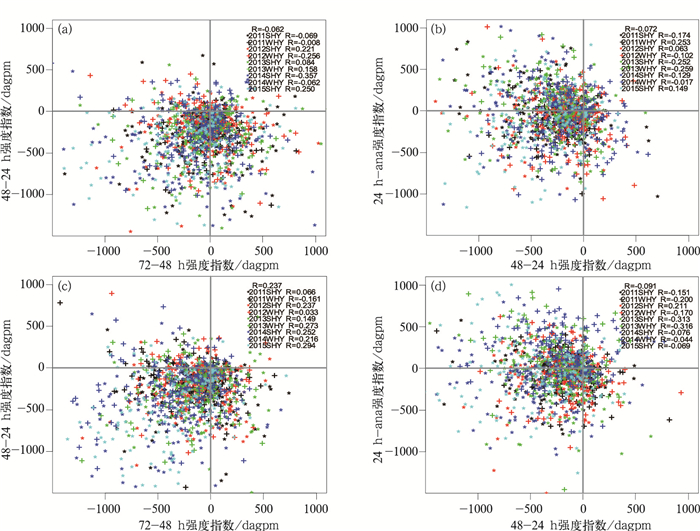
EC模式72 h时效内预报，副高西脊点随时效临近逐渐往西调整、强度逐渐增强、北界逐渐北移，可否利用这一特征对24 h时效的预报误差24 h-ana(ana：分析场)进行预估，需要分析不同时效的调整趋势之间是否存在相关性。图 4所示为ECMWF模式08和20时起报、不同时效副高强度指数相邻时效之间调整趋势的散点图。可见，对于不同的起报时刻、不同年份、不同季节，副高强度相邻时效的调整趋势之间，并没有显著的相关关系，相关系数大都在±0.3以内，一半情况下甚至在±0.1以内。说明不同季节、不同起报时刻、不同版本的模式，副高72 h时效之内的预报，并没有较为显著的、一致的调整趋势。另外，从图 4可见，72-48 h和48-24 h的副高强度指数调整趋势，大部分为负值，说明存在负的系统性偏差，与图 3b中的结论一致，但两者之间的相关性很低，说明两者之间不存在较强的一致变化的特征, 不能用后者的偏弱幅度估计前者的偏弱幅度。24 h-ana的正负值频率接近，与图 3b中强度指数24 h-ana接近于0的系统性偏差一致。

分析EC模式副高面积指数、北界指数和西脊点的调整趋势(图略)，其特征和强度指数的特征相似，不同年份、不同季节、不同起报时刻的不同时效的相关系数都比较小，没有明显的相关关系。同时副高72和48 h时效预报存在面积偏小、位置偏南偏东的系统性的偏差。

可见，EC模式08和20时起报的对副高的预报，72 h时效内，整体上存在西脊点偏东、北界偏南、强度偏弱、面积偏小的系统性偏差，且这一系统性偏差随时效的延长而增大。即不同时刻的预报可表示为：

$ {F_t} = A + {a_t} + {\sigma _t} $

式中，A为实况，a_t为系统性偏差常数，σ_t为随机误差。由于a_t随时效的临近而逐渐减小，导致日常检验业务中表现出“随着预报时效的临近，副高范围逐渐增大、强度逐渐增强、位置逐渐西伸北扩”(图 3c)的特征。估计副高24 h的预报误差，相当于预估a₂₄和σ₂₄，a₂₄作为系统性误差，可以运用滑动训练期等方法，通过分析一段时间的F_t-A得到(董全等，2012)，而图 4中的分析显示，σ₂₄, σ₄₈-σ₇₂和σ₇₂-σ₄₈三者之间并没有较为显著的相关性，因此并不能用前面时刻的调整趋势估计后面时刻的调整趋势。即副高强度随时效临近而“增强”的程度，各时效几乎是随机的。这一特征和Hamill(2003)的研究结论一致。

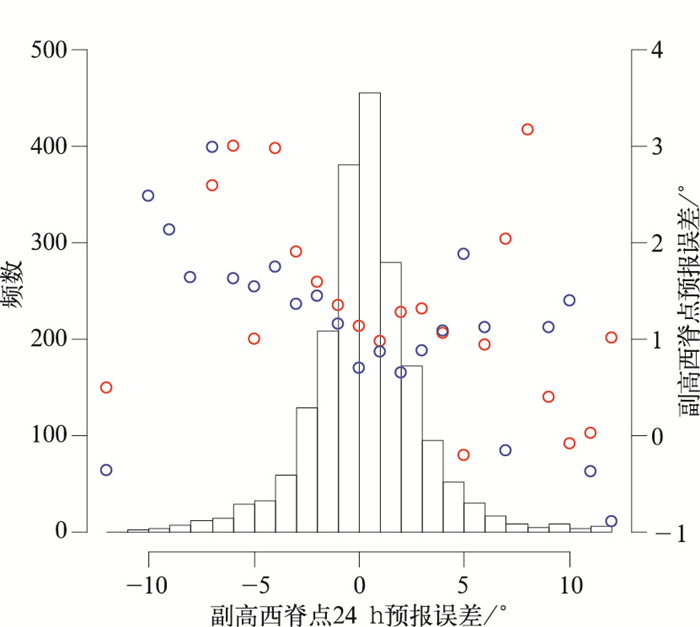
图 5所示的柱状图为EC模式24 h时效副高西脊点预报相对于分析场的误差的频数，图中红色点和蓝色点分别为副高西脊点24 h预报误差位于该区间时对应的48-24 h和72-48 h调整趋势的平均值。可见，副高西脊点24 h预报误差为负的时候，对应48-24 h和72-48 h副高西脊点调整趋势的平均值都为正，反映出图 3c中48-24 h和72-48 h西脊点系统性偏东的特征。意味着当副高西脊点72-48 h和48-24 h都偏东时，24 h-ana可能偏西。当副高西脊点24 h预报误差为正的时候，72-48 h和48-24 h副高西脊点调整趋势并没有随24 h-ana的增大而一致地增大或减小，甚至在部分时候72-48 h和48-24 h的副高西脊点调整趋势平均值为负，即副高西脊点72-48 h、48-24 h和24 h-ana三者之间并没有一致的持续偏东或偏西的趋势。对副高西脊点各时效调整趋势的进一步分析显示，三个时效都为正(负)的调整趋势的样本仅占20.9%(2.0%)，可见三个时效的预报同步往西调整的样本仅有五分之一，而同步往东调整的样本几乎为零，也说明“副高随时效临近逐步西伸”的特征仅仅是系统性偏差导致的。因此，无法用前一时效的调整趋势较为有效地估计后一时效的调整趋势。另一方面，24 h时效西脊点预报误差的频率分布显示，24 h西脊点预报并无明显的系统性偏差，更多地表现为均值接近于0的随机正态分布(图 5)。

EC确定性模式最后一次升级是在2015年5月12日(http://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-model/cy41r1-summary-changes)，取2015年5月15日至9月30日20时起报的趋势调整资料，一方面模式性能是稳定的，另一方面这一时间段处于我国夏季，季节因素可以不考虑，同时剔除了起报时间可能对调整趋势的影响。运用式(1) 分析副高各指数的方差特征。从表 1可见，副高北界72-48 h、48-24 h和24 h-ana三项的调整趋势方差之和(6.41) 与72 h预报误差的方差(5.93) 非常接近，以上三项两两之间的协方差较以上三项的方差都小一个量级。分析20和08时其他年份不同季节、不同时效副高北界调整趋势的散点图和各自的相关系数(图略)，部分时候在0.2左右，大部分情况下在0.1左右，与表 1中结论一致。因此可以近似认为副高北界逐时效的调整趋势之间是相互独立的。副高西脊点48-24 h和24 h-ana的调整趋势之间有较明显的负的协方差，其他两个协方差项都接近于0(表 1)，说明副高西脊点48-24 h的调整趋势和24 h的预报误差之间有较显著的负的相关性。进一步分析副高西脊点20和08时起报的其他年份不同季节、不同时效调整趋势的相关系数(图略)可以发现，部分年份、部分季节，不同时效的调整趋势的相关系数可以达-0.603(2011年夏半年，20时起报72-48 h与48-24 h)、-0.562(2013年冬半年，20时起报48-24 h与24 h-ana)和-0.548(2014年夏半年，08时起报48-24 h与24 h-ana)，而部分时段相关系数接近于0(0.009：2014年冬半年，20时起报48-24 h与24 h-ana；-0.001:2012年冬半年，08时起报72-48 h与48-24 h)，整体上表现出以下特征：(1) 以负的相关性为主；(2) 夏半年相关性强于冬半年；(3) 不同时段相关系数变化很大，在-0.6~0之间；(4)72-48 h与48-24 h之间的相关性较强的时间段，48-24 h与24 h-ana之间的相关性并不一定强，如表 1中2015年汛期所示。因此，ECMWF模式不同时效副高西脊点的预报，72 h时效内逐24 h的调整趋势之间并没有较好的一致性，因此像图 1所示的副高西脊点随时效的临近，较为一致地逐步往西调整的趋势，并不具有普遍性。但在不同的年份、不同的季节、不同的模式版本下，副高西脊点24 h的预报误差可能与72-48 h或48-24 h的调整趋势之间有较明显的相关性，但这一相关性并不具有较强的普遍性，因此需要进行检验更新。副高西脊点24 h预报误差和长时效预报的调整趋势之间的相关性普遍为负，也说明调整趋势和24 h预报误差之间并不具有一致性，24 h的预报误差往往和之前的调整趋势相反。

如表 1所示，对EC模式20时起报夏季副高西脊点和北界各时效预报误差和调整趋势的平均值来看，北界各时效预报误差和调整趋势的平均值接近于0，说明对副高南北位置预报误差较小，调整趋势也不明显，但西脊点72和48 h时效预报误差大于3个经度，24 h预报误差接近于1个经度，说明副高西脊点预报存在偏东的系统性偏差，且时效越长，这一系统偏差越大，与图 3c结论一致。

表 2所示为2015年5月15日至8月31日，EC模式20时起报，副高西脊点72-48 h和48-24 h的不同调整趋势同时发生的样本数，以及对应此时24 h预报误差分别为正和负的样本数(括号内数字)，其中有效的总样本数为75 d。可见，由于各时效对副高西脊点预报系统性偏东的偏差，有几乎一半(38个)的样本西脊点调整趋势72-48 h和48-24 h为同时偏东，在这38个样本中，对应24(14) 个样本西脊点24 h预报偏东(西)，结论与图 3c一致。

为了剔除副高西脊点系统性偏差对调整趋势一致性分析的影响，各时效预报减去西脊点均值，之后分析各时效的调整趋势。如表 3所示，此时西脊点72-48 h的调整趋势为正和负的样本数接近，24 h预报误差为正和负样本数也接近，而48-24 h的调整趋势为负的样本数(52) 远大于正的样本数(23)，反映出西脊点48和24 h预报之间较强的负的相关性(表 1)。

从表 3还可以看到，系统偏差订正后，当副高西脊点72-48 h和48-24 h的调整趋势都为正的时候，副高西脊点24 h的预报误差为正和负的频率分别为2/15和13/15，几乎都为负，其他情况下，24 h预报为正和负的样本数接近。可见，EC模式升级后，对2015年汛期我国副高西脊点的预报，48和24 h预报具有较显著的负的相关性，72 h时效内逐24 h的调整趋势并不一致，日常业务中表现出的“随时效临近副高逐渐西伸的特征”，是由副高西脊点预报系统性偏东导致的，各时效的调整趋势并不具有稳定而一致的相关性。正如Hamill(2003)对850 hPa气温的调整趋势的分析显示，24 h的预报误差与之前时效的调整趋势之间并没有较强的相关性，在线性的误差订正模型中，引入48 h和(或)72 h的预报，对订正效果几乎无改进。以上对EC模式副高预报调整趋势的分析，得出了类似的结论。

在日常检验业务中常常发现，副高位于不同位置时，位置和强度表现出的调整趋势不同。从表 1可见，EC模式对夏季副高预报的误差主要在副高西脊点，北界的误差很小。因此分析副高西脊点位于不同经度时，西脊点预报误差和调整趋势的特征。如表 4所示，整体上副高表现出西脊点越往东预报误差越小、系统偏差越小的特点。副高西脊点72和48 h预报的系统偏差，在110°E以东在偏东2°和1.5°左右，在110°E以西偏东5.6°和3.5°左右，24 h预报平均误差在90°~100°E内最大，在0.5°左右，其他区域都接近于0，72 h的预报误差在110°E以西明显大于110°E以东。

相对于其他经度区间，西脊点位于100°~110°E，即中南半岛时，西脊点各时效的调整趋势和24 h预报误差的方差最大，并且都与72 h预报误差接近(表 4)，说明西脊点位于中南半岛时，72 h内各时效对西脊点的预报误差和各时效调整趋势都接近。不同时效调整趋势之间的协方差，也较西脊点位于其他区域时明显偏大，且都是负的相关性，量级接近于预报误差的方差或者为预报方差的一半(表 4)。说明副高西脊点位于中南半岛时，其72 h内两两时效的调整趋势之间以负的相关性为主，其中以48-24 h与24 h-ana调整趋势之间的负相关性最为显著，与表 1中结论一致。可见副高西脊点位于中南半岛时，除随时效延长而增大的偏东的系统偏差外，各时效的调整趋势并不一致，且调整趋势的方差与预报方差接近，相邻时效的调整趋势之间有一定的负相关性。

当西脊点位于90°~100°E之间，即东印度洋附近时，西脊点调整趋势的方差明显小于预报方差，但24 h预报方差较大，同时调整趋势的协方差绝对值较西脊点位于100°~110°E时明显偏小(表 4)，可见西脊点位于西印度洋附近时，副高西脊点各时效的调整趋势不明显，明显小于各时效的预报方差，且相互之间无明显的相关性。

当西脊点位于110°~120°E之间，即我国南海时，西脊点调整趋势的方差与预报方差接近，这一特征与西脊点位于中南半岛时类似，但不同时效调整趋势的协方差和方差明显小于后者，说明西脊点位于南海时副高西脊点不同时效预报的误差和稳定性较中南半岛时减小。但调整趋势的协方差，明显小于后者，除西脊点调整趋势48-24 h与24 h-ana之间的协方差外，其他协方差都在2左右(表 4)。说明副高西脊点位于南海时，对于2015年夏季的样本，西脊点48-24 h的调整趋势与24 h预报误差之间有一定的负相关性，其他调整趋势之间没有相关性，与西脊点位于东印度洋时类似。

当西脊点位于120°~130°E之间时，副高西脊点的预报误差和调整趋势的方差最小，在2左右(表 4)，不同时效的西脊点调整趋势之间存在弱的正相关性，在逐日的检验中往往表现为随时效的临近，副高西脊点逐渐西移。

可见副高西脊点不同时效调整趋势之间的关系与西脊点所在的位置有关。这可能是由90°~130°E之间复杂的地形所致，从西往东，从印度洋过渡到中南半岛，再到南海，再到菲律宾群岛，再到西太平洋。其中副高西脊点在中南半岛时，受地形影响，EC模式对副高位置预报的稳定性最差，72 h时效内，不同时效的预报方差和调整趋势的方差接近，调整趋势之间存在一定的负相关性。因此对于这一区域的副高订正，构建时间滞后的集合预报是一个值得研究的方向。另外，当副高西脊点位于菲律宾以东的西太平洋时，EC模式对副高预报稳定性明显提高，预报误差和调整趋势的方差显著减小，调整趋势之间以正相关性为主。可见模式预报的稳定性受海陆差异等下垫面影响明显。

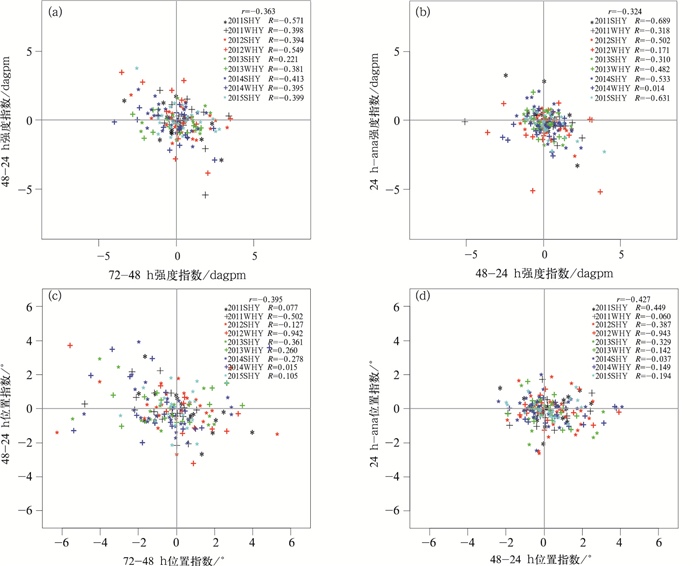
2.2 西风槽的预报调整趋势

图 6所示为ECMWF模式20时起报，新疆北部(BJ)的西风带槽的强度指数和位置指数不同时效的调整趋势之间的关系。相对于副高，BJ槽的强度和东西向位置，72-48 h和48-24 h，以及48-24 h和24 h-ana调整趋势之间存在一定的负的相关性，与副高西脊点类似，不同时效调整趋势的相关系数部分情况下达到-0.6左右，大部分情况下小于-0.3，说明BJ槽强度和位置48-24 h的调整趋势往往和72-48 h的调整趋势相反，而24 h-ana的预报误差又往往和48-24 h的调整趋势相反，即如果BJ槽48 h预报较72 h预报强，则24 h较48 h往往弱，而零场较24 h强，如果48 h预报较72 h预报偏东，则24 h较48 h往往偏西，而零场较24 h又偏东。但是BJ槽不同年份、不同季节、不同时效强度和位置的调整趋势之间的相关系数差别较大，在-0.7~0.1之间。虽然整体上BJ槽位置和强度的相邻时效的调整趋势之间是负的相关性，但是在部分时候相关系数为正，例如2013年夏半年强度指数72-48 h和48-24 h之间的调整趋势的相关系数为0.221。2015年夏半年位置指数72-48 h和48-24 h之间的调整趋势的相关系数为0.105。这一现象，一方面是由于对于20时起报的预报，在某一年的冬半年或夏半年，样本量较少，导致估计的相关系数的随机性增大，另一方面，说明这一相关关系与预报时效、季节和模式的版本等因素有关，还可能与气候的年际变化有关，由于数值模式的不完备性，在不同的气候年际变率下，表现出不同的特征。

另外，从散点分布来看，EC模式对BJ槽位置和强度预报不同时效的调整趋势正负值分布较为均匀，并没有表现出类似副高预报中的系统性偏差。从表 5 BJ槽强度和位置不同时效预报误差和调整趋势的平均值来看，强度的平均值接近于0 dagpm，位置的平均值只有72 h预报在-0.5°左右，说明BJ槽72 h预报位置存在偏西0.5°的系统性偏差，其他时效的系统偏差都接近于0。

对EC模式08时起报的BJ槽的位置和强度的不同时效的调整趋势的散点图和不同年份、不同季节的相关系数(图略)进行分析，特征和20时起报(图 6)的相同，说明EC模式08和20时起报对BJ槽的预报不同时效之间的调整趋势并无显著差异。

BJ槽强度和位置，相邻时效的调整趋势整体上为负的特征说明，位置和强度72-48 h的调整趋势和24 h-ana的预报误差之间存在正的相关性。根据式(1)，对72 h时效BJ槽的位置和强度预报误差进行方差分解。由于样本量较少，同时08和20时起报的调整趋势之间无明显差异，因此选2015年5月15日至9月30日08和20时起报的所有样本，有效样本共37个。如表 5所示，对BJ槽的强度预报的方差在1 dagpm左右，而对位置预报的方差较大，72和24 h时效分别在10和2.36°左右。可见对BJ槽的预报，模式的误差主要在槽的位置上，而对BJ槽的强度的预报误差接近于0 dagpm。对于BJ槽位置的72 h预报误差，72-48 h、48-24 h和24 h-ana调整趋势两两之间的协方差较各时效调整趋势的方差小一个量级，接近于0 dagpm，但cov_{72-48, 48-24}的值为正，而cov_{72-48, 24-ana}的值为负，与图 6c和6d中2015年夏半年BJ槽位置指数不同时效调整趋势相关系数为0.105和0.194的结论一致。对于BJ槽强度72 h预报误差，72-48 h、48-24 h和24 h-ana调整趋势两两之间的协方差为各时效调整趋势的方差的1/5左右，与图 6a和6b中2015年夏半年BJ槽强度指数不同时效调整趋势相关系数为-0.399和-0.631的结论一致。但虽然此时BJ槽强度72-48 h和24 h-ana调整趋势之间为正相关，但两者之间的协方差相对于各时效的预报误差而言，差不多小一个数量级，因此无法用这一相关性来对BJ槽强度24 h预报进行订正。分析其他年份不同季节BJ槽强度72-48 h调整趋势和24 h-ana之间的相关性(图略)，除个别年份个别季节外，大部分时间段两者的相关系数为正，大都在0.3以内，从散点分布也可以看出，两者之间的相关性并不十分明显，另外，BJ槽强度24 h-ana的离散度较72-48 h的明显小，说明用72-48 h的调整误差估计BJ槽强度24 h-ana的预报误差，并不会得到较好的估计结果。

可见虽然过去的样本显示，EC模式对BJ槽强度和位置的预报，大部分样本存在“flip-flop-flip”(Zsoter et al, 2009)现象，即48 h预报较72 h预报往东调整，24 h预报较48 h预报往往会往西调整，而24 h预报相对于分析场往往又偏西。但是对于2015年5月13日版本升级后的EC模式系统，不同时效BJ槽的强度和位置的调整趋势并没有表现出以上的特征，相关系数进一步减小到接近于0，同时位置指数72-48 h和48-24 h的调整趋势变为弱的正的相关性。可见数值模式由于受季节、年份、模式版本、气候的年际变化等多种因素的影响，不同时效的预报之间并没有较为一致的调整趋势，或者这一调整趋势与季节、天气系统、数值模式版本、气候的年际变化和季节内变化等因素有关，需要稳定模式版本, 大量的数据样本进行统计分析。

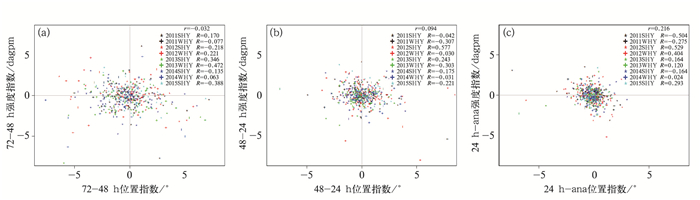
分析同一时效BJ槽的位置和强度的调整趋势之间的关系(图 7)，不同年份、不同季节两者相关系数之间的差异较大，在-0.3~0.5之间，有正的相关性也有负的相关性，同时还有接近于0的相关性，说明同一时效BJ槽的位置和强度的调整趋势之间的关系并不一定，在不同的季节、不同的模式版本，两者之间的关系不同，有时可能不存在相关性，因此不能用BJ槽强度(位置)预报的调整趋势来订正或估计位置(强度)的调整趋势或误差，两者需要分别考虑。

研究对我国天气有较大影响的位于华北(HB)、东北(DB)和四川盆地(SC)的槽，以及南支槽(NZ)，根据式(1) 对72 h预报的位置和强度进行方差分解。为了增加样本，从而使得方差分析具有统计意义，同时尽量剔除季节因素的影响，对于HB槽和DB槽，选取EC模式版本更新后的08和20时起报的2015年5月15日至9月30日的样本，有效样本分别为49和67个，在这一时间段SC槽和NZ槽分别只有1和7个。EC模式上一次模式版本更新为2013年12月1日，因此对于SC槽和NZ槽，选取2013年12月3日至2015年9月30日的样本，有效样本数分别为27和89个。

表 5所示，为以上各槽强度和位置72 h预报误差的方差的分解各项，以及各时效预报误差和调整趋势的平均值。可见，与BJ槽一样，相对于550 dapgm左右的槽强度，华北、东北、四川盆地和南支槽的强度的预报误差和各时效调整趋势的方差都较小，72和24 h预报误差的方差分别为2和0.5左右，且预报误差和方差的平均值都接近于0 dagpm，说明EC模式对我国北方的槽、四川盆地的槽和南支槽强度的预报误差都很小，但与BJ槽不同的是，对以上四个区域的槽，各时效预报都略微偏强，尤其对SC槽，偏强1 dagpm左右，DB槽偏强接近1 dapgm，HB槽和NZ槽偏强不明显。对槽强度预报误差的方差的分解来看，相邻时效的调整趋势之间的协方差以负值为主，个别情况下为接近于0的正的协方差，但协方差的量级相对于预报方差，都小一个量级左右，说明不同时效的槽强度调整趋势之间并没有明显的相关关系，同时负的协方差与BJ槽的特征相似，说明存在一定的“flip-flop-flip”现象，即72 h预报偏强(弱)，48 h预报偏弱(强)，24 h预报再次偏强(弱)，但偏强或者偏弱的幅度随时效临近，整体上呈现逐渐减小的趋势。强度预报方差和协方差最大的是DB槽，不同时效调整趋势之间的相关系数达-0.38。DB槽常常伴随东北冷涡或较为稳定的鄂霍次克海冷涡，受其影响，较强的冷空气自中东西伯利亚南下至我国东北地区，与偏南暖气流汇合，由于冷暖气流剧烈的交汇，所以系统的稳定性较差，导致预报误差普遍较大。对于同样位于北方的BJ槽和HB槽，强度预报方差明显大于位于南方的SC槽和NZ槽。

2.3 T639模式天气系统的调整趋势

中国气象局数值预报中心的T639全球模式，于2013年增加卫星资料同化，2014年4月增加台风初始化，之后模式版本保持了稳定(中国气象局数值预报中心瞿安祥，个人交流)，因此研究2014年4月之后的资料，可以剔除模式版本对预报性能的影响。

作为对比，首先研究模式版本稳定后的2014年和2015年夏季5—9月，副高各指数调整趋势之间的关系，如表 6所示。相对于EC模式，T639模式副高各指数各时效预报误差、调整趋势的方差、系统偏差都明显大于前者，这与日常检验结果一致，对副高的预报，EC模式优于T639模式，且后者的预报误差随时效延长而增大的速度明显大于前者。副高位置和强度各时效预报和调整趋势的系统偏差特征与EC模式一致(表 1)，即副高呈现出系统性的西脊点偏东、面积偏小、强度偏弱的特征，且这一系统性偏差随时效延长而增大，北界位置的系统性偏差不明显。分析T639模式副高西脊点与北界各时效调整趋势之间的协方差，远远小于预报方差和调整趋势的方差，并且小于EC模式各时效调整趋势之间的协方差，说明72 h内副高位置各时效的调整趋势之间没有相关性。可见，与EC模式相同，T639模式对于副高的预报，随时效延长，西脊点偏东、面积偏小、强度偏弱的系统偏差逐渐增大，且T639模式的系统偏差明显大于EC模式，而不同时效的调整趋势之间，并没有明显的相关性，有时候在日常检验中显示的“随时效临近，副高西脊点逐渐西移的趋势”，只是随时效临近，副高西脊点偏东的系统偏差逐渐减小所致。邱学兴等(2012)对T639模式500 hPa高度场预报误差和偏差订正的分析研究也显示，500 hPa位势高度预报普遍偏小，且时效越长偏小越明显，只引入单时效预报的“递减平均法”，对这一系统性偏差有很好的订正效果。与以上本文所得的研究结论一致。

副高西脊点位于不同经度时，分析T639模式对副高西脊点不同时效预报调整趋势(表 7)。首先，副高西脊点预报方差、各时效调整趋势的方差和系统性偏差，整体上呈现越往东越减小的趋势，与EC模式相同，但各区域的预报误差和系统性偏差普遍比EC模式大，与表 6结论一致。其次，T639模式预报方差和调整趋势协方差最大时是西脊点位于90°~100°E之间，即东印度洋附近，而EC模式是西脊点位于中南半岛时预报方差和调整趋势的协方差最大。T639模式西脊点位于东印度洋和中南半岛时的方差和协方差都明显大于EC模式。可见，影响数值模式性能的不仅仅是下垫面或海陆分布，模式版本不一样，或者对下垫面处理过程的不同，会导致不一样的结论。

对于不同时效副高西脊点调整趋势之间的相关性，整体上T639模式72-48 h与48-24 h调整趋势之间的协方差很小，没有明显的相关性(表 7)，而48-24 h与24 h-ana调整趋势之间的协方差明显大于前者，说明T639模式副高西脊点72-48 h的调整趋势，与更临近时效的调整趋势之间接近于相互独立，这与日常检验业务中所显示的T639模式72 h时效之后的预报误差显著增大的特征一致。西脊点位于不同经度范围时，不同时效西脊点预报的调整趋势之间的协方差整体上都以负值为主，尤其是48-24 h与24 h-ana调整趋势之间的协方差，说明T639模式与EC模式相同，相邻时效副高西脊点的调整趋势并不一致，大部分情况下是以“flip-flop”(Zsoter et al, 2009)特征为主，即48 h预报偏东(西)，而24 h预报偏西(东)。

分析T639模式对BJ、HB、DB、SC、NZ槽强度和位置预报调整趋势的特征，如表 8所致。与EC模式相同，整体上呈现出北方槽(BJ、HB、DB)的强度和位置的预报方差和调整趋势的方差大于南方槽(SC、NZ)的特征，但普遍都大于EC模式槽强度和位置的预报误差和调整趋势的方差。另外，槽强度预报的方差和调整趋势的方差在1~3 (dagpm)²左右，相对于槽强度550 dagpm的量级而言明显接近于0，说明T639与EC一样，对槽强度的预报误差很小。对于槽的位置，系统性偏差在-0.5°~-0.1°左右，说明位置普遍略偏西，与西风槽日常检验中的现象一致。对我国不同区域槽不同时效调整趋势之间的协方差，以负值为主，但相对于预报方差，都明显较小，说明T639模式与EC模式相同，槽的强度和位置不同时效预报调整趋势之间，同样没有较为明显的相关性，且负的协方差，说明相邻时效的调整趋势变化并不一致。

3 结论

在西风槽和副高强度、位置等指数定义和自动识别的基础上，对EC和T639模式副高和西风槽以及南支槽随时效临近的预报调整趋势之间的对比分析发现：

(1) EC和T639模式对副高的强度、面积、南北界和西脊点位置的预报，随着时效的临近，并没有较为明显的、一致的调整趋势，但副高的预报两家模式都存在西脊点偏东、范围偏小和强度偏弱的系统性偏差，且时效越长这一偏差越大，T639模式的偏差明显大于EC模式。

(2) 副高的预报误差和调整趋势的特征，与西脊点所处的经度有关，从东印度洋到菲律宾以东洋面，西脊点越往东，预报误差和系统偏差越小，但在东印度洋和中南半岛，调整趋势之间的协方差，两家模式表现出了一定的差异，同时，在不同的区域，不同时效的调整趋势之间都没有明显的相关性，且整体上以负的协方差为主，说明不同时效的调整趋势并不一致。

(3) 对于西风槽，两家模式都表现出北方的槽的误差明显大于南方槽的误差，强度的误差可以忽略不计的特征，且T639模式的误差明显大于EC模式。对于槽的东西向位置而言，没有明显的系统性偏差，相邻时效的调整趋势之间以负的协方差为主，说明随时效的临近，槽的位置并没有较为一致的调整趋势。

(4) 不同时期EC和T639模式，对副高和西风带槽不同时效预报的调整趋势之间，并没有表现出显著的差异，相关系数都接近于0，说明模式版本的升级或者不同的模式版本，不同时效的调整趋势之间都没有显著的相关性。