引言

降水预报是现代天气预报重要业务之一，随着经济和技术的发展，政府和公众对降水预报准确率和精细化水平的需要越来越高。数值预报为降水预报提供了最有价值的参考，日常业务中预报员会基于自身经验和前期模式表现对模式降水强度和落区进行调整，从而进一步提高模式降水预报准确率。随着数值模式预报性能不断提升，仅采用上述主观定性的订正方式来实现预报员对模式的订正技巧已变得越来越难(Stuart et al, 2006; Turco et al，2010)。因此有必要对模式预报的降水强度以及落区偏差进行系统性的分析。一方面可为预报员订正模式提供误差背景，实现预报员在模式预报基础上的附加值；同时也可为模式研发者和定量降水客观预报产品的研发提供有价值的模式偏差信息。

随着模式分辨率的不断提高，传统点对点的评分检验方法，如TS评分等，将会导致双惩罚现象(Ebert et al，2000)。为了更好地解决降水检验中双惩罚的问题，近年来一些新的检验技术如空间检验技术开始在定量降水预报检验中使用，这些方法能提供更详细的模式预报偏差信息(Wernli et al, 2009；刘凑华等，2013)。目前大致有17种空间检验技术，Gilleland等(2009)对现有的空间检验技术进行了对比分析，将这些方法大致分为两大类，一类为滤波的方法，而滤波方法又包括邻域和尺度分离技术，另一类为位移的方法，包含基于目标和场形变技术。CRA(contiguous rain area)空间检验技术(Ebert et al，2000；2009) 属于基于目标的空间检验方法，该方法可输出降水目标的落区、强度以及形态误差，该误差信息可为预报员订正模式提供最直接的参考。

西南地区东部是我国暴雨的频发区。由于地形和影响系统的复杂性，在这一地区主、客观预报都没有较好的预报能力(宗志平等，2013)。符娇兰等(2014)发展了一种面向对象的雨带识别和拟合检验技术，对2012年汛期西南地区东部5次强降水过程进行了检验，结果表明在中短期时效内，模式均对西南地区雨带位置预报偏北偏西，对大雨及以上量级降水量预报较实况偏弱，小雨及以下量级的降水范围预报较实况偏大。由于仅分析了几个个例，检验结论是否具有代表性，仍需要对大量个例进行系统性分析。与此同时，上述5个个例均有高空槽或高原槽影响，且低层配合有低涡切变线的发展，那么不同影响系统造成的降水预报误差是否存在差异也是值得探讨的问题。Williams(2013)利用空间检验技术对美国东部32个温带气旋降水个例的预报偏差进行了评估，表明模式对此类个例的降水面积预报偏大。Yost(2013)利用空间检验技术对美国多家业务模式中尺度对流系统造成的降水位移误差进行了分析，指出NCEP-GFS、EC等全球模式预报的中尺度雨带较实况偏北。马力(2012)将四川盆地暴雨环流形势分为六种类型：西部阻塞型暴雨、川东-江淮切变型暴雨、西风带大槽型移动性暴雨、两高切变型暴雨、高压后部型暴雨、南风型暴雨。并指出后三类预报难度较大，容易造成漏报，可见有必要对不同影响系统的降水误差进行分类分析。为了进一步简化问题，本文将按照影响系统和降水分布特点将西南地区东部强降水个例分为三类，分别为：西南地区东部低涡切变型、西南地区东部-江淮切变型、南风型，然后分别对这三类强降水的误差进行检验评估。

利用基于对象的CRA检验技术，通过选取西南地区东部2011—2014年强降水天气个例，对相应的EC细网格模式36 h时效的24 h累积降水进行检验，重点分析模式落区和强度误差。通过环流分型将强降水分为三种类型，进一步探讨不同类型模式预报偏差，从而为预报员认识不同影响系统下的模式误差提供依据。

1 资料选取及检验方法介绍

本文主要针对西南地区东部2011—2014年5—9月强降水个例的模式降水预报误差进行检验分析，共选取了128个区域性大到暴雨的降水个例。个例选取标准为西南地区东部(24.5°~33°N、100°~110°E)24 h累积降水有3个及以上站点出现暴雨及以上量级降水均为一次区域性大到暴雨过程。考虑到EC模式总体预报性能较好，在业务中得到普遍应用，本文主要针对EC细网格模式的24 h累积降水量预报误差进行检验，检验的预报时效为36 h。实况降水为全国2400多个站点的24 h累积降水，利用基于变分技术的插值方法将站点降水插值到模式格点场上(刘凑华等，2013)。

CRA方法是由Ebert等(2000)提出一种基于目标的定量降水检验方法，检验对象为单个降水目标或雨带，而不是整个降水场，因此更便于预报员理解模式对于不同影响系统下的降水误差。通常情况下，模式对某一具体降水目标有预报能力，仅仅是在落区和强度上存在一定的误差。在这种情况下，传统的检验方法存在双惩罚现象，一方面在实况有降水的地方存在漏报，另外一方面在没有降水的地方存在空报，导致传统的两分类预报评分很低，从而认为该预报为一次失败个例，但实际上该预报对预报员具有很高的参考价值，预报员只要了解了模式落区和强度偏差，就可以在此基础上进行订正从而做出较为准确的预报。

CRA检验方法首先用某一降水阈值来定义连续雨区(contiguous rain area，简称CRA，该方法因此而得名)，本文降水阈值取为25 mm·(24 h)^-1, 然后对某一区域(本文选取区域为24.5°~33°N、100°~110°E)连续雨区进行识别和分离，要求连续雨区覆盖范围大于2°×2°网格。在此基础上，分析计算识别出的雨区范围内实况和模式的降水质心、25 mm降水面积、平均降水量、最大降水量以及面总降水量。为进一步分析模式误差来源，对CRA内相应的模式预报进行平移，最大可在原有连续雨区上向各个角度平移5°，当平移后模式预报与实况之间方差达到最小时，则该平移距离即为模式的位移误差。由此可将模式降水预报误差分解为位移误差、强度误差以及形态误差，见式(1)。其中总误差为原始模式预报(f_i)与实况(O_i)偏差平方和的平均数，见式(2)。

$ MS{{E}_{\text{total}}}=MS{{E}_{\text{displacement}}}+MS{{E}_{\text{volume}}}+MS{{E}_{\text{pattern}}} $

(1)

$ MS{{E}_{\text{total}}}=\frac{1}{N}\sum\limits_{i=1}^{n}{{{({{f}_{i}}-{{O}_{i}})}^{2}}} $

(2)

平移后的误差为平移后的模式预报(f′_i)与实况偏差平方和的平均数见式(3)。

$ MS{{E}_{\text{shift}}}=\frac{1}{N}\sum\limits_{i=1}^{n}{{{(f{{\prime }_{i}}-{{O}_{i}})}^{2}}} $

(3)

$ MS{{E}_{\text{displacement}}}=MS{{E}_{\text{total}}}-MS{{E}_{\text{shift}}} $

(4)

位移误差是将平均总方差减去平移后的平均总方差，见式(4)。

$ MS{{E}_{\text{volume}}}={{\left(\overline{f\prime }-\bar{O} \right)}^{2}} $

(5)

强度误差为平移后的模式平均降水强度减去实况强度的平方, 见式(5)。

$ MS{{E}_{\text{pattern}}}=MS{{E}_{\text{shift}}}-MS{{E}_{\text{volume}}} $

(6)

形态误差为平移后误差减去强度误差, 见式(6)。

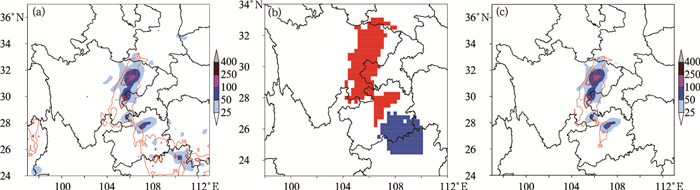
从128个个例中共识别出138个连续雨区(CRA)，其中有9个个例识别出来的CRA不满足最小范围的要求，实际上只有119个个例识别出了有效的CRA。图 1a为2011年5月2日实况和相应的模式36 h预报降水分布，主观上可以看出一条雨带位于四川盆地中东部至贵州北部，另一个雨带则位于广西北部至贵州南部。图 1b为经识别和分离后得到的两个CRA，整体上与主观分析较为一致。图 1c是按照方差最小的标准平移北侧降水目标后(向东向北分别调整了0.5°后)模式与实况的分布，可见经平移后降水落区与实况更为接近。

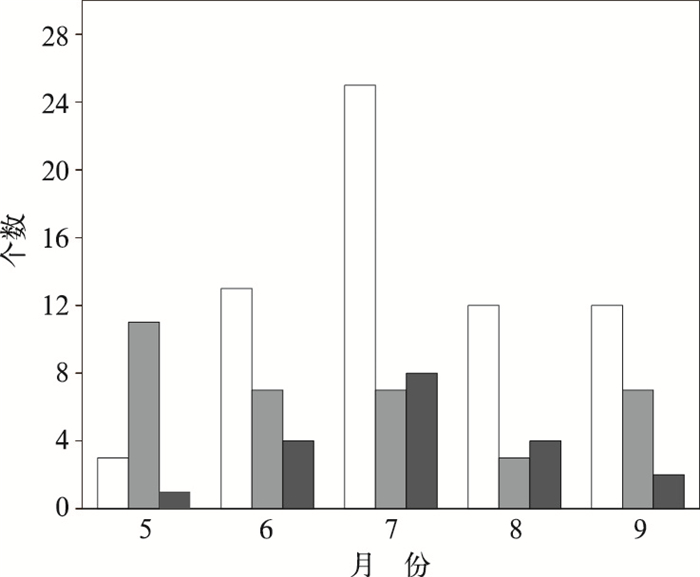
为进一步分析不同环流形势模式预报误差，按照引言中的分类方法对能有效识别到CRA的119个个例进行分类，分类后的个例分别为西南地区东部低涡切变型65个、西南地区东部-江淮切变型35个、南风型19个。图 2给出了各类型降水个例逐月分布情况，第一类降水各月都有可能出现，主要出现在6—9月。第二类型降水主要出现在5—7月和9月，尤其是5月主要以第二类降水为主，此类降水过程一般有较明显的冷空气活动，因此春末夏初或初秋更容易发展。第三类型降水主要出现在6—8月，此时对应副热带高压或者大陆高压较强，有利于南风型强降水个例的出现。三种类型的降水之间虽然具有明显区别，但彼此并不是完全孤立的，同一次天气过程在不同阶段有可能由一种类型演化为另一种类型(马力，2012)，如可能前期为南风型，后期演变为西南地区东部低涡切变型，或者前期为西南地区东部低涡切变型、后期演变为西南地区东部-江淮切变型。

2 西南地区东部强降水预报总体误差分布

从西南地区三种误差分布可以看出(表 1)，形态误差占比最大，为60%左右，其次是落区误差，约为30%左右，强度误差最小，约为10%，这与Ebert等(2000)的误差分布不同，其形态误差小于落区误差。降水的形态特征主要与中尺度对流系统活动有关，这可能与本文检验对象为全球模式有关，全球模式由于其分辨率等因素会造成降水更平滑，从而对降水的中尺度特征刻画不足。

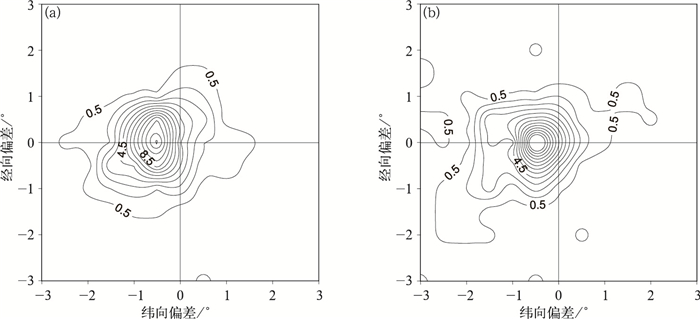
从模式和实况大雨雨区的质心偏差可以看出，模式在西南地区东部预报的强降水总体落区较实况偏西，表明模式可能预报雨区向东移动偏慢。模式预报偏南偏北的概率相当，表明模式不存在系统性的经向偏差(图 3a)。位移(落区)误差同样表明模式预报大部分个例的落区较实况偏西(图 3b)，平均偏西约0.7°，最大可达2.0°左右，而经向的平均位移偏差约为-0.05°，无明显的系统性的经向偏差(表 1)。

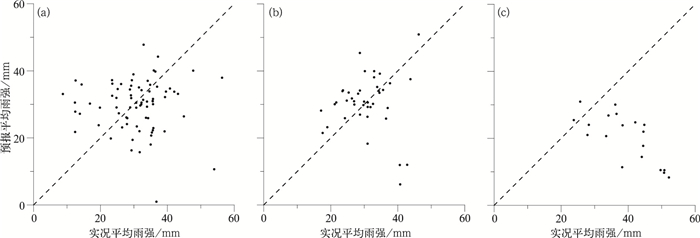
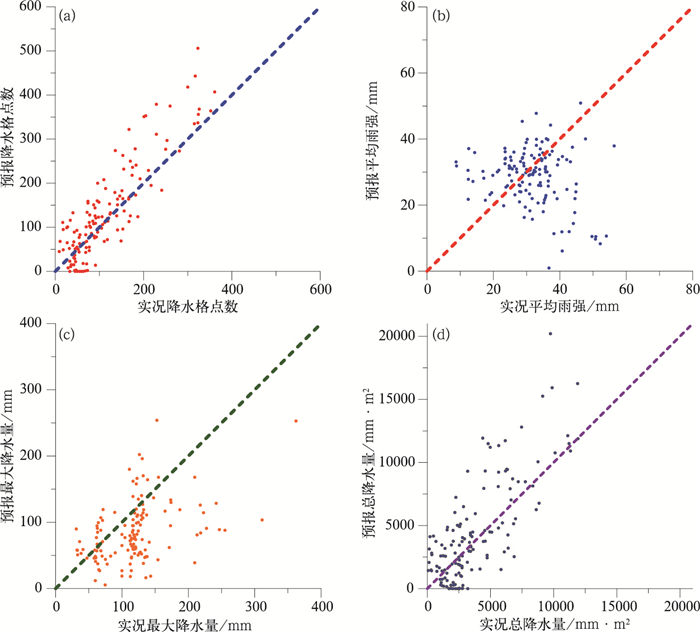
模式预报的大雨以上量级的范围总体较实况偏大，模式预报的面积较平均实况偏大约30%(图 4a)。实况雨区格点数大于200个(长约700 km以上的雨带，即α中尺度雨带)均预报偏大，而对于β中尺度雨带(格点数少于50个，雨带宽约200 km)，有50%个例模式预报偏小，其中有5个个例未预报出相应的大雨以上量级雨区。因此模式对于不同尺度雨带预报误差不一致，这可能与全球模式对中尺度系统预报存在明显偏差有关。从平均降水量来看(图 4b)，除模式空报一部分大雨以上量级的降水以外，当实况出现大雨以上量级的降水，大部分个例模式预报的平均降水强度较实况偏弱。而从最大值预报来看(图 4c)，模式预报的普遍较实况最大降水偏小，平均偏小约20%，这可能与模式倾向于将小量级的雨区范围预报偏大，而对于大量级的预报不足有关(Ebert et al, 2000)。而对于总降水量(平均降水乘以格点数)(图 4d), 模式总体预报大，即模式内部大气水分循环总体偏湿，其中对于小于10000 mm·m²的总降水量，模式预报的总降水量与实况基本一致，但大于10000 mm·m²的总降水量，模式普遍预报偏大，即模式对于天气尺度降水天气总体上预报是面积偏大，总降雨强度偏强，这与前面的分析是一致的。

3 西南地区东部不同环流型强降水预报误差对比分析

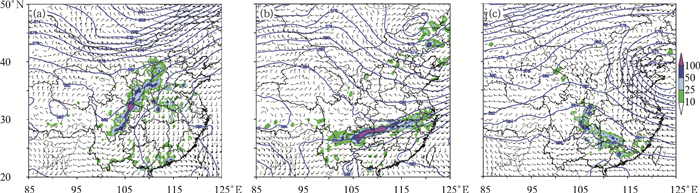
按照上面的环流分型，图 5给出了每一类型相应个例的降水分布和环流形势。可以看出第一类环流形势呈东高西低分布(图 5a)，高原槽东移影响西南地区，我国东部为高压脊，天气尺度系统移动缓慢，受高层低槽动力强迫导致对流层中低层西南涡发展，强降水主要位于低涡及其切变线附近，雨带整体呈东北—西南向。通常这种形势能维持几天从而导致四川盆地等地持续性的强降水。第二类环流形势呈南高北低型(图 5b)，中高纬有西风槽东移，副热带高压位于华南沿海，从而导致冷暖空气交汇于我国南方地区，西南地区东部主要受对流层低层冷式切变线影响，强降水主要位于切变线附近及南侧低空急流左侧辐合区，雨带呈准东西向。这类降水通常伴随着冷空气的南下表现出移动性的特征。第三类主要表现为南风里的对流性降水(图 5c)，500 hPa通常无明显的低槽系统，西南地区东部主要受高压脊控制，对流层中下层受高压后部东南风或西南风影响，降水主要位于南风辐合区或者受地形抬升较为显著的区域，降水对流性质明显，分布较为分散，局地性较强。从天气学检验来看，模式对于第一类、第二类的降水事件通常具有一定的预报能力，主要表现出落区和强度方面的误差，而对于第三类降水事件多数情况下模式无预报能力，多为漏报。下面将利用CRA空间检验技术对三类不同降水事件的预报误差进行定量化分析。

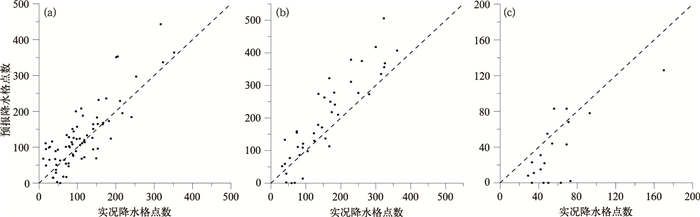
从模式预报与实况的大雨以上量级面积可以看出，对于第一类强降水个例，60%以上个例模式预报面积较实况偏大，而预报偏小的个例集中在格点数小于200，即降水目标水平尺度越大，模式预报偏大的可能性较大(图 6a)。第二类强降水个例与第一类降水个例模式预报偏差有相似的特征，约80%个例模式预报面积较实况偏大，偏小的个例主要集中在尺度较小的降水事件(图 6b)。而对于南风型强降水事件，80%个例模式预报面积较实况偏小，与第一类和第二类降水个例误差正好相反，这可能与南风型的降水事件水平尺度较小，常由暖区内中尺度系统带来的对流性降水有关，从天气学检验评估来看，模式对这一类型的降水预报能力较弱，常表现漏报(图 6c)。

图 7给出了模式预报与实况的平均降水强度，对第一类强降水事件，当降水目标实况平均降水强度不大( < 30 mm)，模式预报偏强的概率较大，而对于实况平均强度>30 mm的降水事件，模式预报的强度弱于实况的概率明显增大(图 7a)。第二类降水事件的平均降水强度预报偏差与第一类类似，对于强度偏小的降水事件，模式容易预报偏强，而对于强度较强的降水事件，模式预报较实况偏弱(图 7b)。与降水面积类似，第三类降水事件模式预报的降水平均强度明显弱于实况(图 7c)。

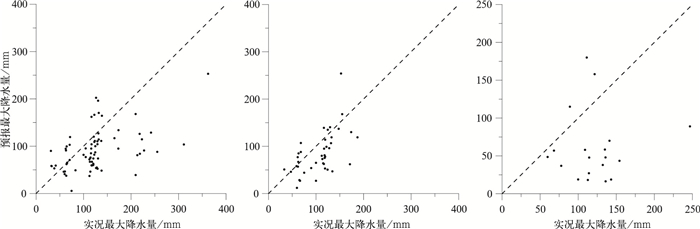
对于最大降水量的预报偏差(图 8)，三类降水事件表现出类似的特征，模式预报的最大降水量较实况偏弱的概率非常大，约80%以上。且实况强度越强，模式预报偏弱的可能性越大，而模式预报较实况偏大主要集中在实况降水强度相对较弱(100 mm以下)的个例。

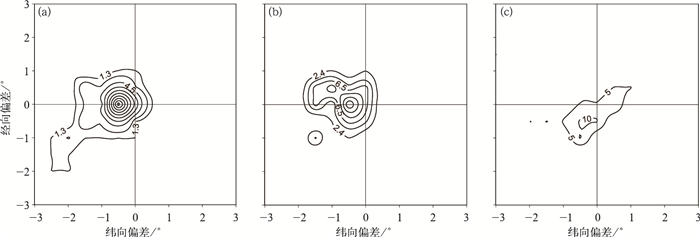
图 9给出了不同环流形势下的降水个例落区误差或位移误差分布，可以看出西南涡及切变型降水落区偏西特征非常明显，占比80%以上，其中偏西0.5°~1°概率最大，约50%左右，最大偏西幅度可达2.5°~3°，无明显的偏南或偏北的倾向(图 9a)。这与宗志平等(2013)的天气学检验评估结论和符娇兰等(2014)对2012年典型个例的降水误差定量化检验结论基本一致。而对于江淮切变型降水落区以偏北偏西特征为主，占比75%以上，其中偏西、偏北0.5°~1.5°概率最大，约40%左右，最大幅度可达2°~3°(图 9b)。对于南风型降水个例，以偏西、偏南特征为主，占比60%以上，最大幅度可达1°~2°(图 9c)。不同类型降水出现降水落区误差的差异，很有可能与模式预报的天气尺度系统出现了偏差，即模式可能预报系统移动速度较实况偏慢；此外，这些类型的降水通常都伴有较强的对流性降水，模式参数化出来的降水与实际由中尺度系统产生的对流性降水存在较大差异，从而导致整体降水落区出现偏差。

4 结果与讨论

本文选取了2011—2014年5—9月128个强降水个例，利用CRA空间检验技术对上述个例ECMWF细网格模式预报的36 h降水进行检验，通过识别得到119个降水目标，在此基础上对上述降水目标的降水落区、强度误差进行了统计分析。根据环流形势和影响系统的不同，对上述强降水目标进行分型，并进一步对不同类型强降水的落区、强度误差进行对比分析，得到如下结论：

(1) 西南地区强降水个例的预报误差中，形态误差占比最大，为60%左右，其次是落区误差，约为30%左右，强度误差最小，约为10%。降水的形态特征主要与中尺度对流系统的活动有关，这可能与全球模式对降水的中尺度特征刻画不足有关。

(2) 对西南地区东部而言，模式预报的强降水存在偏西的落区误差，平均约0.7°，无明显的经向误差倾向。模式对于不同尺度雨带强度预报误差不一致，对于水平尺度较小的降水目标漏报概率较大，而对于天气尺度降水目标模式预报面积偏大，总降水量偏大；但从平均降水量和最大降水强度预报误差来看，总体而言模式预报较实况偏弱，且实况越强，偏弱的概率越大。

(3) 根据西南地区东部环流形势和影响系统分布特征，将强降水事件分为三类，西南地区东部低涡切变型、西南地区东部—江淮切变型、南风型。从强度上来看，第一类和第二类强降水事件预报面积和平均强度误差类似，模式预报面积偏大的可能性较大，且降水尺度越大模式往往预报面积越大。而实况强度越强，模式往往预报平均强度越偏弱，而对于强度相对较弱的个例，模式预报偏强的概率明显增大。第三类强降水模式预报的面积和平均强度均偏弱，出现漏报的概率较大。而对于最大降水量，三类个例模式预报的最强降水均较实况偏弱。从上述强度预报偏差统计来看，预报员在使用模式时，建议对于第一类和第二类降水个例可将模式预报的大雨范围基于形势分析进行适当的缩小，而对于降水强度很强的降水过程，可能要将降水量级在模式的基础上往大的量级订正。而对于第三类降水个例，模式往往出现漏报，因此预报员要基于形势、对流产生的环境和触发条件的诊断分析，判断有出现暖区对流性降水的可能，在此基础上在模式预报的基础上将降水范围和强度往大的方向进行调整。

(4) 从三类强降水的落区误差可以看到，西南地区东部低涡切变型降水落区误差以偏西为主，偏西0.5°~1°概率最大，偏南或偏北的倾向不明显。而西南地区东部-江淮切变型强降水落区误差以偏西偏北为主，偏西偏北0.5°~1.5°概率最大。对于南风型降水个例，以偏西偏南特征为主。基于上述落区误差统计特征，预报员可基于形势分析对模式强降水落区误差进行相应的调整。

CRA技术是对连续雨区进行检验，主要是用于天气尺度降水误差的分析。对于中尺度降水，应根据检验目标的时空尺度需要进一步对降水阈值、最小降水面积、目标匹配标准、搜索半径等参数调整(Grams et al, 2006)。而对于局地分散型降水该方法的适应性需要进一步研究。

模式降水预报误差成因很多，如初始场误差、动力场预报误差、积云参数化和微物理参数化过程造成的误差，对地形刻画不够精细等(Ebert et al，2000)。只有更好地理解模式产生云和降水的物理过程，才能更好地理解模式误差成因。符娇兰等(2014)对2012年几次典型的低涡切变型强降水个例的降水落区偏西的成因进行了探讨，认为模式预报的天气系统偏慢导致了降水预报偏西。本文仅仅分析了降水预报误差统计特征，未来还需要进一步通过典型降水个例的形势场预报误差分析、逐3 h模式格点和对流性降水和实况降水的对比分析、不同模式物理参数化方案和不同分辨率地形的降水预报性能评估，从而进一步分析模式降水误差成因及其局限性，为预报员提供订正模式预报的科学依据。