引言

蒸散(Evapotranspiration，ET)是指土壤蒸发(Evaporation，E)和植物蒸腾(Transpiration，T)的总和，其大小与下垫面条件、各种气象因子以及植物的生理特性有密切关系。在农业生产中，蒸散直接反映了作物的需水情况，获得准确的实际蒸散量对于指导农业生产中的水分利用，制定合理的灌溉制度，监测农田旱情，研究农田作物生育期的水分消耗规律，提高水分利用效率具有十分重要的意义(汪明霞等，2006)。

实际蒸散量的获取主要有两种方式，一种是理论估算，一种是直接观测。目前实际蒸散的估算方法，通常是通过订正参考作物蒸散的间接计算，即先计算参考作物蒸散，然后根据实际土壤水分状况和作物生长状况，乘以土壤水分胁迫系数和作物系数进行订正。直接观测方法包括大孔径闪烁仪(LAS)、涡动相关仪(EC)和大型称重式蒸渗仪(Lysimeter)等，其中, 基于水量平衡原理的称重式蒸渗仪法是测定蒸散最为传统, 也是最为精确的方法之一(汪秀敏等，2011；葛帆等，2004)。

蒸散理论估算的方法主要包括Penman、FAO Penman-Monteith(FAO P-M)、Priestley-Taylor(P-T)、1955 Mc FAO、Blaney-Criddle(B-C)、Hargreaves(Har)、Thornthwaite等。FAO Penman-Monteith法综合考虑了影响蒸散的各种因素，是目前国际上公认的参考蒸散计算的标准方法，在我国的蒸散计算中也得到了广泛的应用(曾丽红等2011；段春锋等，2011)，但是FAO Penman-Monteith公式计算需要大量的气象数据，数据观测资料缺乏地区难以使用，实际应用中也因为数据过多不够方便灵活，因此受到很大的限制。

为研究蒸散计算方法在不同地区的适用性，当前有很多蒸散公式比较的研究(曹金峰等，2015；Schneider et al，2007；张晓琳等，2012；杜尧东等，2001；毛飞等，2000；刘倪等，2009；刘安花等，2010；邵小路等，2013)，但基本上都是采用FAO Penman-Monteith法的计算结果作为评价其他方法的标准，如秦鹏程等(2014)以FAO Penman-Monteith模型计算的参考蒸散结果为标准，比较了Priestley-Taylor、Hargreaves及Thornthwaite三种模型在湖北省的适用性，表明在湖北省气象资料匮乏或不便应用的情况下，作物模拟模型及气候变化等研究中宜采用Priestley-Taylor估算模型，日常干旱监测及水资源规划中宜采用Hargreaves模型，干湿气候区划等工作中可采用Thornthwaite模型；秦年秀等(2010)比较了以气温为基础的Thornthwaite和Blaney-Criddle公式、以辐射为基础的Makkind和Priestley-Taylor公式在贵州地区的适用性, 结果表明, 与Penman-Monteith公式计算结果相比, 以辐射为基础的蒸散公式在该地区的适用性较好, 以气温为基础的蒸散公式用于气候变化情景下潜在蒸散量预测, 结果偏大；Zhao等(2009)研究了土壤水量平衡法、波文比法、Priestley-Taylor方法、Penman方法、Penman-Monteith方法与Hargreaves方法在黑河流域的适用性，结果表明，Penman-Monteith方法计算较为准确，Priestley-Taylor方法和Hargreaves方法与Penman-Monteith方法结果较为接近可以作为替代方法。

FAO Penman-Monteith方法的计算结果受到气象数据观测资料的限制，计算结果也并不是完全准确，采用FAO Penman-Monteith方法的计算结果作为评价其他方法的标准具有一定的误差。蒸渗仪是测定蒸散最为精确的方法之一，在目前基于蒸渗仪实测结果对蒸散计算方法进行比较的研究很少，袁小环等(2014)应用蒸渗仪实测方法评价FAO Penman-Monteith、Hargreaves、Priestley-Taylor、Penman-van Bavel模型在北京地区潜在蒸散(ET₀)计算中的准确性，结果表明，Penman-van Bavel模型准确性最高，其次为Penman-Monteith模型；徐俊增等(2010)在蒸渗仪实测的基础上评价了11种ET₀计算方法在我国东部湿润地区的适用性，结果表明，FAO Penman-Monteith方法与实测值最为接近，综合法中的1948 Penman法、辐射法中的Priestley-Taylor法和FAO24 Radiation法、温度法中的Turc法也能取得较好的结果，而Hargreaves法、FAO24 C Penman法、Mc Cloud法计算结果较差。但这些研究都是对参考蒸散估算的比较，关于实际蒸散法估算的研究很少。

因此本文以河北省怀来地区为例，基于蒸渗仪实测数据，评价FAO Penman-Monteith(FAO P-M)、Hargreaves(Har)、Priestley-Taylor(P-T)方法在计算实际蒸散中的适用性，分别从月、日尺度上分析三种方法的准确性，并探讨实际蒸散的主要影响因素。对于准确地估算作物实际蒸散量，加强水资源管理、制定合理的灌溉计划具有十分重要的意义。

1 研究区域与方法 1.1 研究区域与数据 1.1.1 研究区概况

研究区位于河北省怀来县中国科学院怀来遥感综合试验站(40°20′N、115°47′E)，地处延庆盆地，两侧山地西南—东北走向, 试验站位于盆地西南段，西距官厅水库约2 km。研究区属温带、半干旱大陆性季风气候，年平均气温约10.1℃，夏季最高气温39℃，冬季最低气温可达-20℃以下；降水主要集中在夏季，年平均降水总量约370 mm，年平均风速3.4 m·s^-1。土壤以沙质褐土为主，主要种植单季夏玉米，品种为郑单958，每年5月初播种，10月初收获(杨光超等，2015；郑秋红等，2006)。

1.1.2 数据观测

北京师范大学与德国干利希研究所合作于2011年，在研究区安装了两台表面积为1 m²，深度1.5 m的蒸渗仪，蒸散测量精度为0.1 mm。两台蒸渗仪共用一个维护井，维护井内安装了两个渗漏桶，用于蒸渗仪的渗漏量测量，测量精度为0.01 mm。此外，两台蒸渗仪内均安装有土壤水势、土壤温度、土壤湿度、土壤热通量传感器。在生长季一台蒸渗仪种植玉米，另一台蒸渗仪表面保持裸土。为了保证在试验期间蒸渗仪内玉米和周围农田玉米生长条件一致，蒸渗仪内玉米的品种、播种时间、行距和株距同周围农田一致，并且定期对蒸渗仪内土地进行除草，尽量保证蒸渗仪内玉米生长同周围农田一致(杨光超等，2015)。

蒸渗仪的计算是以水量平衡公式为基础(刘波等，2010)：

$ ET = P + I - R - \Delta D - \Delta S $

(1)

式中，ET为蒸散，本研究所用蒸渗仪1 kg质量变化对应为1 mm的土壤水分变化；P为降水量，包括降雨和露水；I为灌溉量；R为地表径流量；ΔD为渗漏量；ΔS为蒸渗仪土柱质量的变化。由于在研究区农田内，降雨不足以产生地表径流，所以径流可忽略。

自蒸渗仪架设以来，运行情况良好，本文蒸渗仪数据来自种植玉米的蒸渗仪2013年生长季获得的数据。

蒸渗仪北侧2.8 m处架设了10 m气象塔，其上安装有自动气象站，其可获取蒸渗仪观测期间的气象数据包括净辐射R_n、土壤热通量G、空气温度T_a、相对湿度RH、风速W_S、土壤水分θ(杨光超等，2015)，可用来计算实际蒸散。

1.2 实际蒸散计算方法

本文采用单作物系数法来计算实际蒸散，作物的实际蒸散通过参考蒸散量ET₀乘以作物系数K_c再乘以土壤水分胁迫系数K_s来计算(Allen et al, 1998)：

$ E{T_a} = {K_c}{K_s}E{T_0} $

(2)

式中，ET_a为实际蒸散量；ET₀为参考蒸散量；K_c为作物系数, 是表土干燥而根区土壤平均含水率满足作物蒸腾时ET_a/ET₀的比值; K_s为土壤水分胁迫系数, 反映根区土壤含水率不足时对作物蒸腾的影响。

土壤胁迫系数K_s由下式计算：

$ {K_s} = {\theta _{(0\sim 40{\rm cm})}}/{\theta _f} $

(3)

式中，θ_(0~40cm)为0~40 cm土壤含水量，θ_f为田间持水量；当供水充足(土壤含水量大于田间持水量)时，K_s=1。

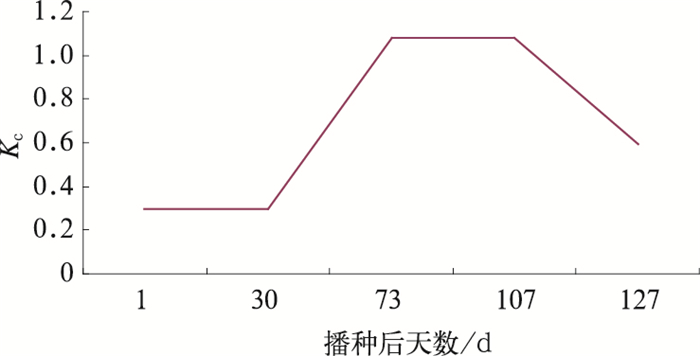
在计算夏玉米K_c值时，将生育期分为生长初期、快速生长期、生长中期和生长后期阶段四个不同生长阶段。FAO推荐夏玉米标准作物系数为：K_cini= 0.3；K_cmid=1.2；K_cend=0.6。

通过FAO推荐方法进行订正后：K_cini=0.3; K_cmid=1.08；K_cend=0.595。作物系数曲线如图 1。

1.2.1 参考蒸散的计算方法

(1) FAO Penman-Monteith方法(以日为时间步长)(Allen et al, 1998)

$ E{T_0} = \frac{{0.408\Delta ({R_n} - G) + \gamma \frac{{900}}{{T + 273}}{u_2}({e_s} - {e_a})}}{{\Delta + \gamma (1 + 0.34{u_2})}} $

(4)

式中，ET₀为参照腾发速率(单位：mm·d^-1)；R_n为作物表面上的净辐射(单位：MJ·m^-2·d^-1)；G为土壤热通量(单位：MJ·m^-2·d^-1)；T为2 m高处日平均气温(单位：℃)；u₂为2 m高处的风速(单位：m·s^-1)；e_s为饱和蒸气压(单位：kPa)；e_a为实际蒸气压(单位：kPa)；Δ为水汽压曲线斜率(单位：kPa·℃^-1)；γ为干湿计常数(单位：kPa·℃^-1)。

公式(4)中相关变量计算如表 1。

(2) Priestley-Taylor公式

1972年，Priestley和Taylor在Penman公式基础上，假定无平流和水分条件不受限制的情况下建立了著名的Priestley-Taylor方程(Priestley et al, 1972)，算式如下:

$ E{T_{0(P - T)}} = \alpha \frac{\Delta }{{\lambda (\gamma + \Delta )}}({R_n} - G) $

(5)

式中，ET_0(P-T)为日蒸散量(单位：mm)；α为常数1.26；λ为水的汽化潜热(单位：2.45 MJ·kg^-1)；其余参数同FAO Penman-Monteith方法。

(3) Hargreaves公式

FAO Penman-Monteith和Priestley-Taylor方程计算蒸散时均利用能量运动原理，需要大量的、长时间序列的各种气象参数观测资料，而Hargreaves模型(Hargreaves et al，1985)只需空气温度和外太空辐射，因参数容易获取和计算简单而得到广泛应用。

$ E{T_{0({\rm{Har}})}} = 0.0023{({T_{\max }} - {T_{\min }})^{0.5}}({T_{{\rm{mean}}}} + 17.8){R_a} $

(6)

式中，ET_0(Har)为参考作物蒸散速率(单位：mm·d^-1)；T_max为日最高气温(单位：℃)；T_min为日最低气温(单位：℃)；T_mean为日平均气温(单位：℃)；R_a为外太空辐射(或天文辐射)(单位：MJ·m^-2·d^-1)。

1.2.2 统计参数

相对偏差(MSE)、均方根误差(RMSE)和一致性系数(d)被用来评价各计算方法计算结果与实测结果之间的误差以及一致性情况，计算方法法如下(徐俊增等, 2010)：

$ MSE = \frac{{{P_i} - {Q_i}}}{{{Q_i}}} $

(7)

$ RMSE = {\left[ {\frac{1}{N}\sum\limits_{i = 1}^N {{{({P_i} - {Q_i})}^2}} } \right]^{\frac{1}{2}}} $

(8)

$ d = 1 - \frac{{\sum\limits_{i = 1}^N {{{({P_i} - {Q_i})}^2}} }}{{\sum\limits_{i = 1}^N {{{(\left| {{P_i} - \overline Q } \right| + \left| {{Q_i} - \overline Q } \right|)}^2}} }} $

(9)

式中：N为观察次数；P_i为模型计算ET₀数值；Q_i为蒸渗仪实测蒸散数值，Q为Q_i对应的平均值。

通常计算结果的误差(MSE、RMSE)越小，d越大，ET_a计算方法表现越好。本文以RMSE为主要依据，在RMSE比较接近情况下，通过一致性参数进行综合比较。

2 结果与分析

对比蒸渗仪实测数据，通过相关性分析及主要影响因素从月、日时间尺度上来评价Penman-Monteith(FAO P-M)、Hargreaves(Har)、Priestley-Taylor(P-T)三种方法在怀来地区的适用性。

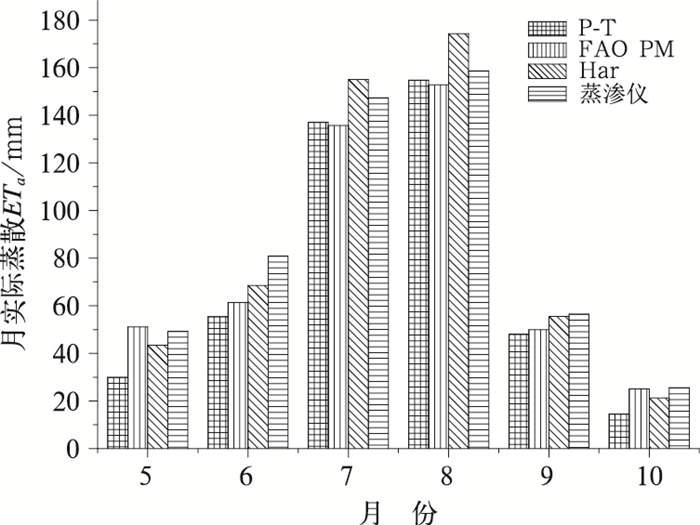
2.1 三种方法在怀来地区的适用性评价 2.1.1 月适用性评价

三种方法计算得到的日实际蒸散，经过进一步累计后得到2013年生长季各月的月实际蒸散，绘制柱状图如图 2，从图中可以看出，三种方法计算的实际蒸散与蒸渗仪实测的蒸散变化趋势基本一致。5月FAO P-M方法计算结果要略高于实测值，其他两种方法低于实测值；6、9、10月，三种方法计算的实际蒸散均低于蒸渗仪实测值；7、8月，Har方法结果要高于蒸渗仪实测结果，其他两种方法仍低于蒸渗仪实测。将三种方法计算的月实际蒸散同蒸渗仪实测数据进行相关性分析及主要影响因素分析，对三种方法的月实际蒸散适用性进行评价。

以蒸渗仪实测值为标准，对各方法计算的实际蒸散进行准确度分析。从表 2中可以看出，三种方法计算的实际蒸散与蒸渗仪实测值均有一定的偏差，且整体要低于蒸渗仪实测值。其中，Har方法计算的实际蒸散偏差最小，P-T方法相对偏差最大。对各方法计算结果与蒸渗仪实测数据进行线性回归, 回归结果见表 3，从均值来看，三种方法计算的月实际蒸散量均值均低于蒸渗仪实测均值，蒸渗仪实测的月实际蒸散均值为86.3 mm, Har方法计算均值为86.3 mm, 与之基本相同；从线性回归曲线斜率可以看出，P-T和FAO P-M方法的曲线斜率均小于1，说明这两种方法计算的实际蒸散整体趋势要小于蒸渗仪实测值，而Har方法的曲线斜率略大于1，说明Har方法计算的实际蒸散整体趋势要略大于蒸渗仪实测值；三种方法线性回归方程的决定系数R²均在0.956~0.990，说明三种方法与蒸渗仪实测数值之间均为较好的线性关系，其中P-M方法计算的实际蒸散量与蒸渗仪实测值之间的线性相关性最好，R²为0.981，Har方法的决定系数R²相差不大为0.978，而P-T方法最小为0.956；三种方法的均方根误差差别较大，P-T最大，为14.907，FAO P-M次之，为9.941，Har方法最小为9.200；FAO P-M方法和Har方法的一致性指数差别很小，但均高于P-T方法。综上，在月实际蒸散的计算过程中，从相关系数来看，FAO P-M方法的表现要略好，从RMSE、MSE和d来看均是Har方法表现最好，但P-T方法始终误差最大。

2.1.2 日适用性评价

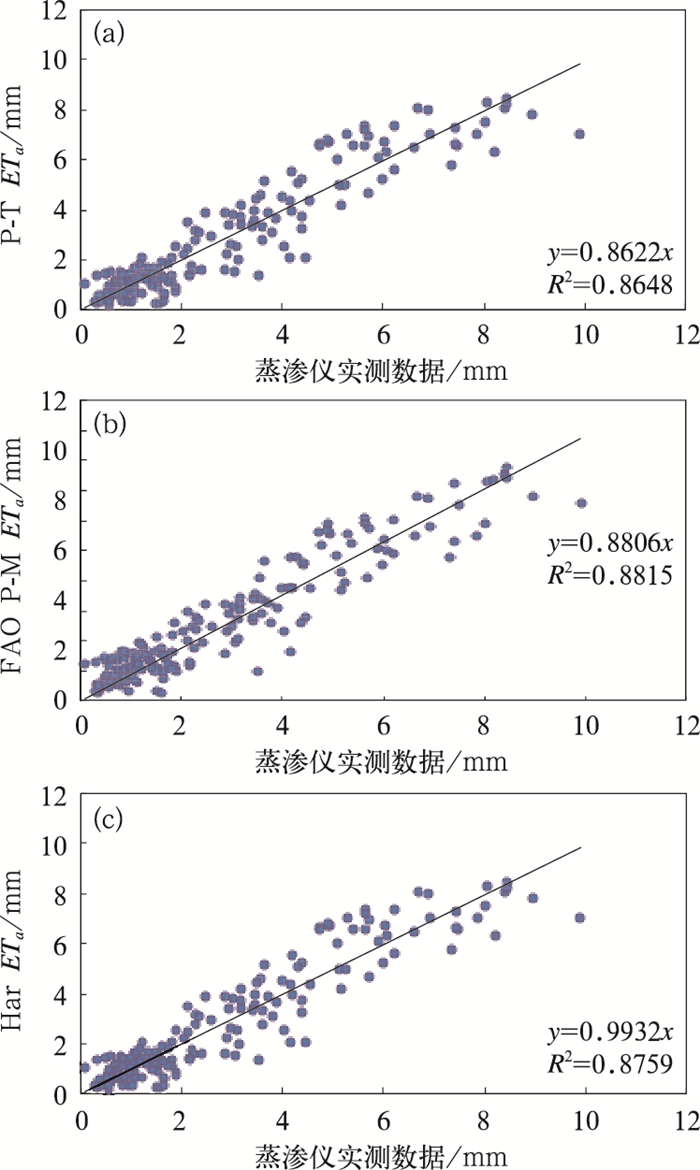
以蒸渗仪实测的夏玉米实际日蒸散量为依据，比较三种不同计算方法的实际蒸散量计算结果，如图 3所示。从图可以看出，三种计算方法的得到的日实际蒸散与蒸渗仪实测结果具有很好的线性关系，相关系数均达到0.85以上，其中FAO P-M方法与蒸渗仪实测结果结果的相关性最好，数据点在线性趋势线周围的分布最为紧凑，Har方法次之，而P-T方法与蒸渗仪实测结果相关性稍差，数据点在线性趋势线周围的分布较为分散。从线性回归曲线的斜率来看，Har方法与蒸渗仪实测结果最接近，其次是FAO P-M方法，P-T方法偏差最大。与实测结果相比，三种计算方法均出现了不同程度的低估。在蒸发能力较低的阶段，计算结果与实测结果较为吻合，而在高蒸发能力阶段，计算结果偏差较大。

就均方根误差而言，FAO P-M方法最小为0.806，其次为Har方法0.837，P-T方法均方根误差最大，达到0.933；从一致性指数、平均相对偏差和均值来看，Har方法表现最好，其次是FAO P-M方法。Har方法一致性指数最高为0.967，FAO P-M方法次之，为0.964；P-T方法一致性指数最小为0.955。Har方法的平均相对偏差最小，为0.068，FAO P-M方法次之，为0.107，P-T方法平均相对偏差最大为-0.127。蒸渗仪实测日实际蒸散平均值为2.793，与之最为接近的是Har方法计算的2.819，其次为FAO P-M方法，P-T方法相差最大(表 4)。

综上所述，在计算怀来地区夏玉米日实际蒸散时，FAO P-M方法、Har方法表现较好，准确度相差不大，从相关系数和均方根误差来看，FAO P-M方法在计算夏玉米日实际蒸散中表现更好一点，而从一致性指数、平均相对偏差来看Har方法更为接近。不管从哪个角度P-T方法准确性都较差。

2.2 影响怀来地区实际蒸散的主要气象因子

太阳辐射、温度、空气湿度、风是影响植物蒸腾与水分蒸发的主要因素(曾丽红等, 2010; 李林等，2000)。为了分析各气象因子对怀来地区蒸散的影响，分别对蒸渗仪实测的月、日实际蒸散与主要气象因子进行相关性分析，结果如表 5，从表中可以看出，二项式拟合比线性拟合的决定系数要有所提高，蒸渗仪实测的月、日实际蒸散量与净辐射的相关性最好，说明净辐射是蒸散的直接驱动力，是影响实际蒸散的主要因子；与温度的相关性较好，说明温度也是影响怀来地区蒸散的主要因子之一；月、日实际蒸散与空气湿度的相关性都较弱，日、月实际蒸散与风速的相关性较差，在线性拟合下甚至表现为负相关关系。其原因主要是由于蒸散的主导控制因素为水分和能量，湿度和风速为一般因素；在怀来地区玉米生长季大风天气常常伴随着降雨，降雨天气蒸散值往往较小，从而削弱了风对蒸散的影响，导致风速与蒸散相关性较差，甚至出现负相关的情况。综合以上分析，说明怀来地区影响实际蒸散的主要气象因子为净辐射和温度。对怀来地区实际蒸散量与净辐射和平均温度进行多元线性拟合(表 6)，决定系数分别为0.821(月)、0.702(日)，说明怀来地区蒸散量与辐射和温度之间具有很好的相关性。

目前估算蒸散方法用的最多的是FAO P-M方法，综合考虑了各项因子对蒸散的影响，结果较为合理，是目前普遍认为最准确的估算方法。Har方法的准确性只与温度和辐射有关，因此，蒸散与辐射、温度的相关性越高，Har方法计算结果的可信度越高，在怀来地区，蒸散主要受辐射和温度的影响，与其他因子相关性不大，说明Har方法计算的怀来地区蒸散量具有很高的可信度，从而也说明本文适用性比较结果是值得相信的，即在计算怀来地区夏玉米日实际蒸散时，FAO P-M方法、Har方法的准确度相差不大。

3 结论

综合月、日时间尺度上夏玉米实际蒸散的评价结果，在计算夏玉米实际蒸散中准确性最高的是FAO P-M方法和Har方法，P-T方法准确性最差。在月尺度上，从相对偏差、均方根误差以及一致性指数来看，Har方法均优于FAO P-M, 但相关性系数方面FAO P-M方法表现稍好；在日尺度上，从相对偏差和一致性指数上看Har方法表现较好，而FAO P-M方法在相关系数、均方根误差上优于Har方法。但考虑到Har方法所需参数较少，计算简便，准确性与FAO P-M方法相差不大，在计算量方面占有很大的优势，因此，在计算怀来地区夏玉米月、日实际蒸散时Har方法有更好的适用性。