2. 中国气象局公共气象服务中心, 北京 100081;
3. 中国气象科学研究院灾害天气国家重点实验室, 北京 100081
2. Public Meteorological Service Centre, CMA, Beijing 100081;
3. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
流域面雨量是指流域内单位面积上的降水量,是水文预报模型中最重要的输入因子,也是各级政府和有关部门组织防洪抗旱以及中小河流洪水、山洪地质灾害预警防治等决策的重要依据。流域面雨量估算与预报涉及多学科且技术难度较大,其精确性很大程度上取决于流域空间降水估测和预报(徐晶等,2007)。
起初国内的流域面雨量估算多依赖于地面气象站的降水观测。然而,由于地面气象站网密度相对较低,地面气象站空间分布不均匀,地理位置复杂,以单一的地面常规观测资料为主的流域面雨量估算时空精度难以满足水文业务的要求;卫星遥感监测资料时空分辨率高,覆盖面广,但精度有限;天气雷达监测能够提供高时空分辨率的降水信息,但覆盖率有限,将三者融合进行流域定量降水估测,结果将更为可靠。国外很多地方以雷达、卫星估测降水资料为主,结合地面常规气象站和加密自动气象站降水观测资料快速融合估算面雨量的技术早已完成并实现了业务化运行。我国自2010年前后开始开展基于多元观测降水融合研究,目前,国家级的融合卫星遥感、雷达监测和地面气象观测资料的定量降水估测(QPE)产品已开发完成并入业务化,这为流域面雨量估算提供了数据基础。
然而,就目前研究进展而言,面向流域面雨量的QPE的应用研究还处于起步阶段,其对流域面雨量开发的适用性还有待于进一步确认。在参考管成功等(2006)、赵琳娜等(2010)沈艳等(2013)研究基础上,本文利用多种适用性评估(肖丹等,2010;张亚萍等,2013;翟丹华等,2015)和优化订正(李莉等,2011;吕晓娜等,2013)方法,对国家气象中心开发的QPE产品进行了面向流域的适用性总体评估和订正,并建立了基于QPE的多级流域面雨量产品,最后通过水文要素预报检验,分析了其对水文模式预报改进效果。以期通过对QPE产品进行系统性的检验和订正,为其进一步深入应用提供依据和借鉴。
1 研究区域和数据本文选取我国七大江河流域(张国平等,2010)为研究区域(图 1)。研究时段为:2012年1月至2013年12月。采用的实况降水资料来自水利部水文局提供的流域降水资料(约4万个站),全国每日08时的24 h降水。
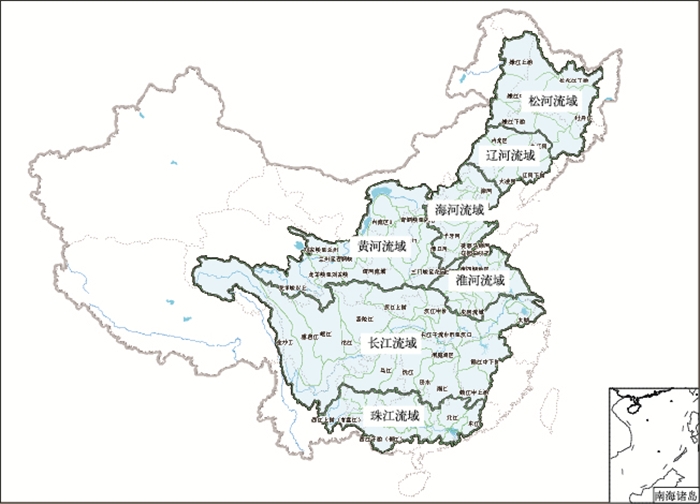
|
图 1 全国七大江河流域示意图 Fig. 1 Sketch map of seven major river basins in China |
选用国家气象中心和国家气象信息中心两套QPE资料。
国家气象中心研发的定量降水估测产品(QPE1):该产品是应用多源概率密度函数算法,在提高卫星和雷达降水估计精度的基础上,融合地面雨量计资料,得到覆盖中国和周边海区的、高时空分辨率的QPE1产品。QPE1的空间分辨率为0.1°×0.1°,时间分辨率为60 min。
国家气象信息中心研发的定量降水估测产品(QPE2):该产品利用美国气候预测中心研发的全球30 min、8 km分辨率的CMORPH卫星反演降水产品和全国3万多个自动气象站观测的小时降水量产品融合,空间分辨率也为0.1°×0.1°,时间分辨率为60 min。
2 面向流域定量估测降水检验 2.1 检验方法目前对QPE产品的检验评估主要是单站评估,由于QPE产品的空间分辨率较高,这里取水文站周边4个格点的平均值作为插值结果。将QPE产品插值到水文站点进行面向江河流域检验。这里对QPE进行总体评价,参照分级降水检验的TS评分、命中率、漏估率、空估率、估测偏差等,此外使用绝对误差、相对误差、均方根误差及ROC曲线等统计方法,对比检验QPE1和QPE2产品,以探究降水真值和定量估测降水的统计特征(刘静等,2012;田付友等,2010;方慈安等,2003;徐晶等,2001;王运生等,2007)。
采用绝对误差、相对误差、均方根误差及平均误差对七大流域QPE1降水进行检验,公式如下:
| $ 绝对误差:{\mathit{X}_\mathit{a}}{\rm{ = }}\sum\limits_{\mathit{i}{\rm{ = 1}}}^\mathit{N} {{\rm{|}}{\mathit{X}_{\rm{f}}}{\rm{ - }}{\mathit{X}_{\rm{o}}}{{\rm{|}}_\mathit{i}}} {\rm{ }} $ | (1) |
| $ 相对误差:{\mathit{X}_\mathit{b}}{\rm{ = }}{\mathit{X}_\mathit{a}}{\rm{/}}{\mathit{X}_{\rm{o}}} $ | (2) |
| $ 均方根误差:{{\mathit{X}}_{\mathit{c}}}\rm{=}{{\left[ \frac{1}{\mathit{N}}\sum\limits_{\mathit{i}\rm{=1}}^{\mathit{N}}{\rm{(}{{\mathit{X}}_{\rm{f}}}\rm{-}{{\mathit{X}}_{\rm{o}}}\rm{)}_{\mathit{i}}^{2}} \right]}^{1/2}}\rm{ }\!\!~\!\!\rm{ } $ | (3) |
| $ 平均误差{\rm{:}}{\mathit{X}_\mathit{d}}{\rm{ = }}\frac{1}{\mathit{N}}\sum\limits_{\mathit{i}{\rm{ = 1}}}^\mathit{N} {{{{\rm{(}}{\mathit{X}_{\rm{f}}}{\rm{ - }}{\mathit{X}_{\rm{o}}}{\rm{)}}}_\mathit{i}}} $ | (4) |
式(1)~式(4) 中,Xf表示降水估测值,Xo表示观测降水值。误差值越小表示估测结果越好。
采用TS评分分析方法来判定降水估测产品,TS评分公式如下:
| $ \mathit{TS} = {\mathit{N}_\mathit{A}}/({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{B}} + {\mathit{N}_\mathit{C}}) $ | (5) |
式中,NA表示降水估测和实况降水均在某一降水范围内的站(次)数,NB表示空估站(次)数,NC表示漏估站(次)数,ND表示降水估测和实况降水均不在某一降水范围内的站(次)数。TS值在0~1,值越大表示估测结果越好。
另外,本文采用漏估率、空估率、估测偏差、命中率、均方根误差、绝对平均误差分析方法来判定降水估测产品,评分公式如下:
| $ 漏估率:\mathit{PO} = {\mathit{N}_\mathit{C}}/({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{C}}) $ | (6) |
| $ 空估率:\mathit{FAR} = {\mathit{N}_\mathit{B}}/({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{B}}) $ | (7) |
| $ 估测偏差:\mathit{BIAS} = ({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{B}})/({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{C}}) $ | (8) |
| $ 命中率:\mathit{POD} = {\mathit{N}_\mathit{A}}/({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{C}}) $ | (9) |
式(6)~式(9) 中,漏估率、空估率、命中率值在0~1,估测偏差>0,其中漏估率、空估率和估测偏差的值越小,命中率的值越大说明降水估测效果越好。此外,研究采用的工作特征曲线(receiver operating characteristic curve,ROC)分析方法最初应用于雷达信号接收能力评价,后来被广泛应用于医学诊断试验性能的评价(管成功等,2006;赵琳娜等,2010)。ROC曲线是以预测结果的每一个值作为可能的判断阈值(本文指的是QPE降水的估算结果),以假阳性率即(1-特异度)为横坐标,以真阳性率即灵敏度为纵坐标,绘制得到相应的灵敏度和特异度变化。ROC曲线下的面积即为AUC值(area under curve)。AUC是很好地衡量模型预测准确度的指标,其取值范围为[0.5,1],值越大表示模型判断力越强。理想情况是QPE估测降水与实际水文站降水完全吻合,此时AUC值为1。文中假阳性率即未发生某个量级降水的因子被正确估测的比例,真阳性率即发生了的某量级降水被正确估测的比例。
| $ \begin{array}{l} 真阳性率(TPR)即命中率:\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{TPR} = {\mathit{N}_\mathit{A}}/({\mathit{N}_\mathit{A}} + {\mathit{N}_\mathit{C}}) \end{array} $ | (10) |
| $ \begin{array}{l} 假阳性率(FPR)即错误命中率:\;\;\;\;\;\;\;\;\;\;\;\;\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{FPR} = {\mathit{N}_\mathit{B}}/({\mathit{N}_\mathit{B}} + {\mathit{N}_\mathit{D}}) \end{array} $ | (11) |
2012和2013年汛期(5—9月)306 d的七大流域时空平均QPE1产品检验结果表明(表 1),七大流域的均方根误差在5.86~12.17,其中长江流域误差值>10,珠江流域也接近10,估测降水在这两个流域上误差较大,而QPE1产品对于黄河、辽河流域和松花江流域的估测能力略强,其均方根误差较小;估测降水的绝对误差2.97~5.33,与均方根误差对应的是,其在长江流域和珠江流域误差较大;估测降水平均误差普遍小于0,说明QPE1估测降水值普遍比实况值偏小;降水估测相对误差为1.13~1.84,相对误差平均值1.49,在各大流域误差相当。从这四个指标综合来看,对于整个样本检验结果在我国偏北的辽河、黄河等流域的估测效果较好,而对于偏南的长江、珠江效果相对差一些。我国南北方差异大,特别是汛期,南方平均日降水量大,降水范围广,尤其长江和珠江流域整个汛期一直处于强降雨带中,北方则平均日降水量少,由此可知,QPE1对降水量级大的区域估测能力相对较弱。
|
|
表 1 2012和2013年的5—9月面向七大流域的QPE1降水检验评估 Table 1 QPE1 precipitation test and evaluation for the seven major river basins from May to September in 2012 and 2013 |
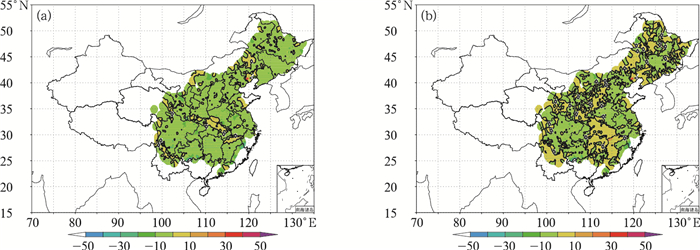
据七大流域QPE1平均误差空间分布看(图 2a),在各大流域上普遍小于水文站观测降水,仅在辽河、黄河、长江上游的部分子流域估测降水比观测值偏大,总体偏差值在10 mm左右。从七大流域QPE1相对误差空间分布看(图 2b),在长江上游流域和黄河流域相对误差较大,在其余流域,误差范围仅在0~4。

|
图 2 2012和2013年的5月1日至9月30日七大流域QPE1平均误差(a,单位:mm)和相对误差(b,单位:%)的空间分布 Fig. 2 Distribution of the average error (a, unit:mm) and relative error (b, unit:%) of QPE1 for the seven major river basins from 1 May to 30 September in 2012 and 2013 |
每年7月底至8月上中旬,随着副热带高压北跳、东亚夏季风向北推进等大气环流形势的改变,我国雨带亦从华南移至华北地区,北方降水明显增多,这一时期我国降水范围大、降水强度也较大。对2012—2013年这一时期的QPE1误差的时间序列进行抽查检验,发现7月下旬至8月上旬与研究时段平均误差、相对误差、绝对误差和均方根误差的结果有相似的趋势,七大流域的QPE1比实况整体偏小,在黄河、松花江及珠江流域中检验效果较好,其他流域次之(图略)。
选取2012年7月20日08时至7月24日08时的一次强降水过程为例,对比分析QPE1和水文站观测降水的空间分布可见,降水带主要集中在黄河、海河、辽河、长江及淮河等流域,呈自西向东、自北向南发展,雨带呈西南—东北走向。20日(图 3b),最大降水值出现在黄河流域陕西、内蒙古交界和长江流域嘉陵江子流域,24 h降雨量达到190 mm,21日(图 3d),降水带东移,降水极大值出现在海河流域,达到398 mm;22日(图 3f),降水开始东移至辽河流域并逐渐减弱,最大降水降为198.5 mm;23日(图 3h),降水中心移到淮河流域,降水为122 mm,之后继续逐渐减弱。对于这个过程的估测,相比水文站观测降水,20日(图 3a),QPE1明显偏弱,并且位置明显偏西,而21日白天(图 3c),即降水最大值当天,QPE1的估测降水位置及降水中心都估测非常准确,降水量364.4 mm,仅略小于观测降水;22日(图 3e),估测降水范围较实况范围偏大,但估测强降水中心仅出现在淮河流域,实际降水中心除去淮河流域的部分区域外,还出现在辽河流域多个子流域中,估测有偏差,估测降水量235.68 mm,略大于实况降水;23日(图 3g),由于实况降水较小,中心较为分散,QPE1估测降水效果不佳。从整个这次降水过程的估测情况看,虽然估测降水和实况存在一定偏差,但估测降水的强降水中心及雨带位置和实况较为吻合,对于降水极大值的估测偏差也较小。
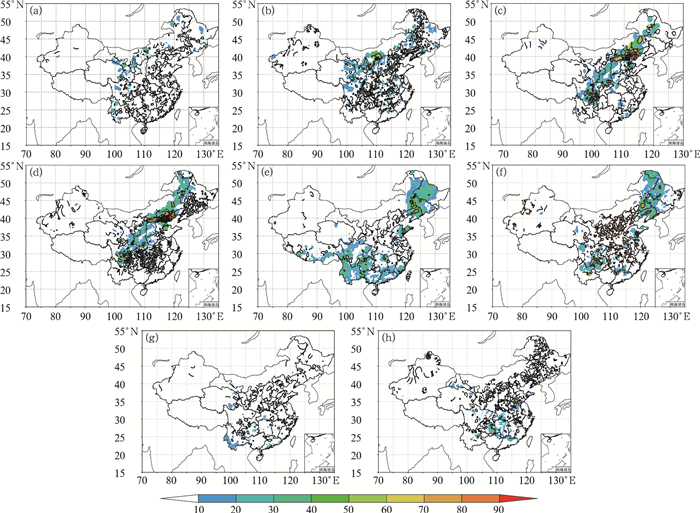
|
图 3 QPE1和水文站观测降水量(单位:mm)对比图(a, c, e, g)7月20—23日QPE1;(b, d, f, h)水文站7月20—23日观测降水 Fig. 3 Comparison of precipitation (unit: mm) of hydrological stations and QPE1 (a, c, e, g) QPE1 in 20-23 July, (b, d, f, h) precipitation of hydrological station 20-23 July |
对七大流域总平均漏估率、平均空估率、平均估测偏差、平均命中率等指标检验QPE1和QPE2降水估测(肖丹等,2010;张亚萍等,2013)。对比结果如表 2所示,QPE1的漏估率均大于QPE2的漏估率,QPE1的空估率在小雨及暴雨以上量级的时候比QPE2较小,而命中率亦普遍低于QPE2;另外,QPE1的估测偏差普遍比QPE2的偏差小,QPE1对量级大的降水估测偏差小,而QPE2对量级小的降水估测偏差小。因此,相较于QPE2,QPE1估测降水则需要进一步优化订正。
|
|
表 2 2012和2013年5月1日至9月30日QPE1和QPE2检验结果对比 Table 2 Test results of QPE1 and QPE2 for different grades of precipitation from 1 May to 30 September in 2012 and 2013 |
通过对QPE1和QPE2的TS评分可见(图 4),各流域QPE1和QPE2的TS评分均随降水量级增大而降低。具体表现为,中雨及其以上量级的估测评分中,与QPE2相比,QPE1的TS估测评分分值明显要小,而当小雨量级时,海河、淮河和黄河流域上的QPE1估测评分要大。QPE1和QPE2的绝对误差和均方根误差在数值上较为相当,QPE2的相对误差明显大于QPE1,此结果与估测偏差结论一致(图 5)。

|
图 4 2012和2013年5月1日至9月30日七大流域QPE1和QPE2的TS评分 Fig. 4 TS score of QPE1 and QPE2 for the seven major river basins from 1 May to 30 September in 2012 and 2013 |

|
图 5 2012和2013年5月1日至9月30日七大流域QPE1和QPE2估测降水的绝对误差(a)、相对误差(b)和均方根误差(c) Fig. 5 Absolute error (a), relative error (b) and root mean squared error (c) of QPE1 and QPE2 for the seven major river basins from 1 May to 30 September in 2012 and 2013 |
图 6为七大流域QPE1和QPE2的ROC曲线。由图可见,在海河、淮河、黄河流域中,QPE1估测ROC曲线下的面积与QPE2估测ROC曲线下的面积相当,估测效果接近;由于ROC曲线下的面积(即AUC的值)越大,表示估测效果越接近真值,所以,在QPE2的ROC曲线面积较大的辽河、松花江、长江及珠江流域,估测效果更接近真值。
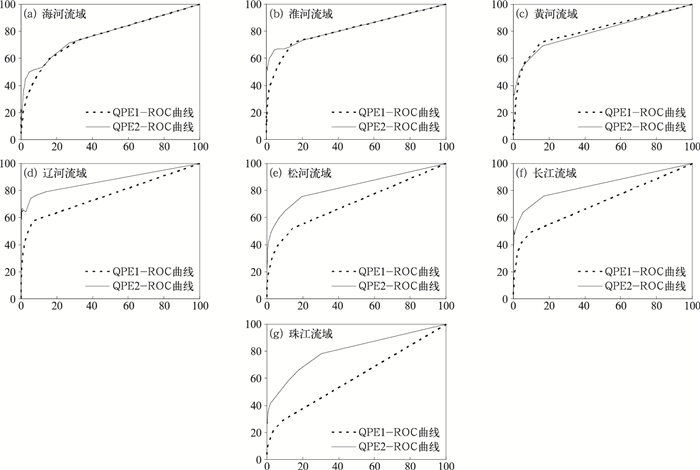
|
图 6 2012和2013年的5月1日至9月30日七大流域QPE1和QPE2 ROC曲线 Fig. 6 ROC curve of QPE1 and QPE2 for the seven major rivers from 1 May to 30 September in 2012 and 2013 |
采用递减平均法(李莉等,2011;邱学兴等,2012),根据每日的QPE和实况降水的误差进行相关统计,并将统计结果直接订正初始的QPE产品。具体方法如下:
(1) 误差估计。计算QPE对于实况降水的误差,记为bi, j,表示如下:
| $ {\mathit{b}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) = {\mathit{f}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) - {\mathit{o}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) $ | (12) |
(2) 误差累加。将最新的各个时次估测误差累加到上一个时次的误差场,得到更新后的误差场。
| $ {\mathit{B}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) = \left({1 - \mathit{w}} \right){\mathit{B}_{\mathit{i}{\rm{, }}\mathit{j}}}\left({\mathit{t} - 2} \right) + \mathit{w}{\mathit{b}_{\mathit{i}{\rm{, }}\mathit{j}}}\left({\mathit{t} - 1} \right) $ | (13) |
式中,w为权重,bi, j(t-1) 为上一时次的误差场,Bi, j(t)为累积后的误差场。
(3) 误差订正。将当日的QPE减去新的误差场得到最终的订正场。
| $ {\mathit{F}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) = {\mathit{f}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) - {\mathit{B}_{\mathit{i}{\rm{, }}\mathit{j}}}\left(\mathit{t} \right) $ | (14) |
式中Fi, j(t)为订正后的QPE。
样本距当日的天数越近,样本所占的权重系数越大, 随着所用样本距当日天数的延长, 其权重系数呈衰减趋势。递减平均天数越短,那么权重系数曲线衰减得越快。
需要说明的是,对于不同的递减平均天数方案, 同一天的样本在不同方案中所占的权重是不同的。本文设计了两种方案:方案一是直接以前一日的误差场为基础进行误差累加,方案二是在前一年平均误差场为初始的误差场为基础,再将前一天的误差场进行不同比例的累加,进行两个方案设计的目的是对比2012年的误差平均对2013年的订正的影响。
3.2 面向流域的QPE1产品订正结果 3.2.1 2013年QPE1订正权重的确定为了确定订正权重系数w,分别计算w等于0.3、0.4、0.5、0.6、0.7、0.8和0.9时,方案一和方案二的订正效果,对订正结果进行误差对比检验,从而根据检验结果确定最优的系数。
从表 3看出,采用方案1随着权重系数的增加,误差平均的绝对值不断减小,w>0.8时,减小的幅度<0.1 mm,w<0.8时,减小的幅度大于0.1 mm,其中w=0.9时,误差平均绝对值最小,为0.69 mm,仅为w=0.3时误差平均的一半;而从相对误差平均来看,w的大小对其影响不大,但呈现负相关的趋势;均方根误差来看,随着w的增加,均方根误差平均相对增大,当w增大到0.9时,均方根误差达14.10 mm。
|
|
表 3 订正后的误差平均、相对误差平均和均方根误差平均 Table 3 Absolute error, relative error and root mean squared error after correction |
从表 3看出,采用方案2随着w的增加误差平均的绝对值也减小,有与方案一相似的趋势,其中w为0.9时,误差平均绝对值最小,为0.69 mm;而从相对误差平均来看,w越大,相对误差呈现出减小的趋势,但变化幅度不大;均方根误差平均随着w的增加而增加,最小值(12.72 mm)与最大值(14.10 mm)相差为1.38 mm。
对比方案一和方案二可见,考虑了2012年方案一的平均误差的总体效果相对于方案二的情况更优,绝对值偏小0~0.13 mm,而相对误差平均和均方根误差平均相对变化不明显。考虑到此种优势不明显,因此在以下的计算中,将不考虑前一年的误差平均,选取方案一进行订正。
综合而言,在不考虑前一年的年平均误差的情况下,运用递减平均法对2013年的QPE1进行订正,相对误差平均在前一日权重系数大时最优,而均方根误差平均呈负相关,综合选取0.6~0.8效果较优,这里选定了0.8为订正权重系数。
3.2.2 2013年QPE1订正结果检验分析根据上述方法确定了订正方案及权重系数,对2013年QPE1进行订正,以2013年水文站24 h降水观测为实况场,订正前后的QPE1场与其进行对比检验。
从表 4中可以看出,未经订正的2013年QPE1误差平均达-3.0 mm,订正后为-0.8 mm,减小了73%,相对误差平均从1.65减小到1.20,减小了27%,均方根误差平均由12.74 mm增加到13.8 mm,增加了约8%,从上述变化可见,订正效果相对明显。
|
|
表 4 QPE1订正前后的误差对比 Table 4 Error analysis of original QPE1 and corrected QPE1 |
从表 5QPE1订正前后不同量级降水相对误差对比结果可以看出,经过订正,大雨以下量级的相对误差改善较为明显,由1.05降低到了0.82,而大雨以上量级效果改善不明显。
|
|
表 5 QPE1订正前后不同降水量级相对误差对比 Table 5 Error analysis of original QPE1 and corrected QPE1 based on different rainfall grades |
对比订正前后2013年QPE1相对误差平均的全国分布图(图 7)可见,订正前,相对误差>3以上的区域主要分布于长江流域和江淮之间,订正后,此区域的相对误差明显改善,大部区域相对误差<3;而东北、华北的相对误差在订正前后无明显变化,相对误差值<3。

|
图 7 2013年订正前(a)和订正后(b)QPE1相对误差的全国分布图 Fig. 7 Spatial distribution of original (a) and corrected (b) QPE1 relative error in 2013 |
对比订正前后2013年QPE1误差平均的全国分布图(图 8)可以看出,订正前,七大江河流域的误差平均出局部区域为正值分布外,全国大部区域均呈负值分布,说明QPE1相对于实况降水明显偏小,并且<-10以上的区域分布与长江流域和淮河流域;订正后,误差平均正值区域明显增加,并且平均值<-10区域明显减小,这是误差平均绝对值订正后明显减小主要原因。
3.2.4 2012年QPE1订正结果检验分析与2013年相同,采用递减平均法对2012年的QPE1进行订正(表略),试验不同的前一日误差权重,根据检验效果试验,确定权重系数为0.7时,检验效果最优。订正前后的误差平均分别为-3.53和-0.44 mm,相对误差平均为1.67和1.21。另外,对2012年个例进行了研究(图略),对于连续性降水,订正后的QPE1在降水的连续性和量值分布上都较订正前有明显的提高,但对于降水仅出现在24 h内的降水,订正效果并不理想,这可能与前期累积误差较小有关。
4 基于定量估测降水的面雨量在水文预报中的个例检验 4.1 试验流域概况本文采用沂河临沂站以上流域为模型应用流域。沂河发源于鲁山南,是鲁南地区跨省最大山洪河道。流域上游以鲁山背斜与潍、猕河为分水岭,东以沂山背斜余脉与沭河为分水岭。河道长287.5 km。地势西北高,向东南部平原倾斜。由于沂河上游地势复杂,形成了许多的支流。流域面积在20 km2以上的一级支流共36条,其中临沂站以上的一级支流有东汶河、蒙河、枋河、涑河、柳青河,流域内山丘面积区约占32%,平原面积区约占68%。沂河流域属温带季风区大陆性气候,多年平均降水量830 mm,汛期降雨量616 mm,约占年降水量的74%。由于QPE的空间分辨率达10 km,因此,本文以QPE在流域的格点平均值作为流域面雨量的值进行计算。
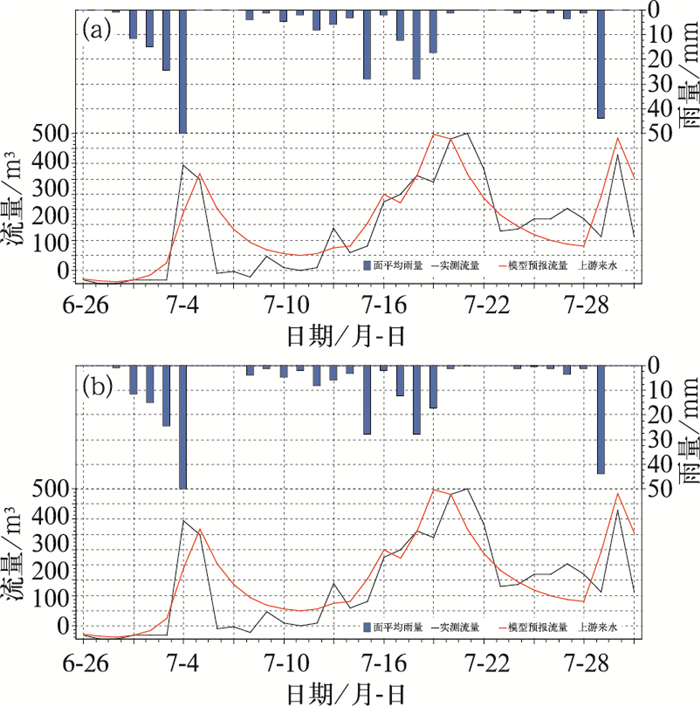
4.2 基于订正前后的QPE1面雨量在水文预报中的检验选取试验流域2012年6月26日至9月30日、2013年6月28日至7月31日的两次流域过程作为检验样本。将订正前后的QPE1计算的面雨量同时应用于这两次过程,选择在中国水文业务中应用最为广泛的新安江水文模型,以水情预报规范标准进行检验(陈丽娟等,2005;李俊等,2012;张亚萍等,2007;程丛兰等,2013)。流域出口临沂站的流量过程由水文站实际观测所得,确定性系数计算公式见式15。具体结果如图 9和图 10。
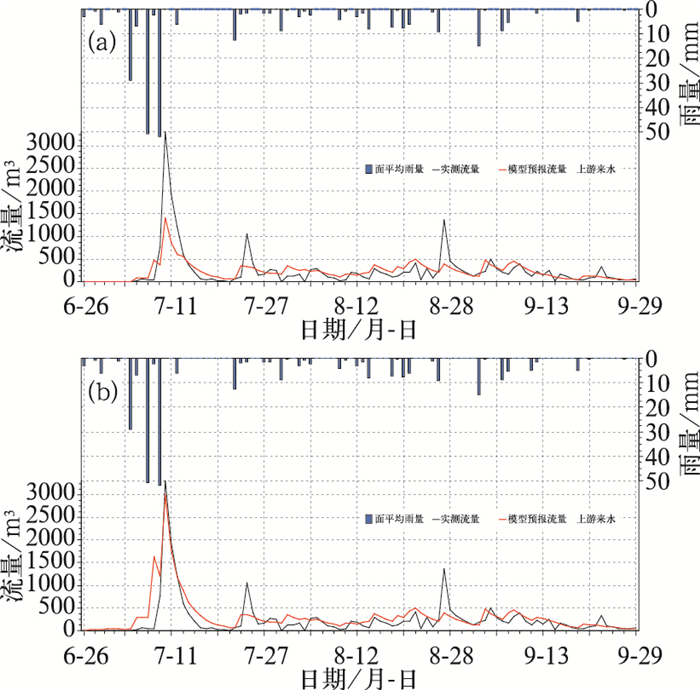
|
图 9 基于QPE1的面雨量在2012年流域水文预报中的预报结果 (a)面雨量在2012年流域水文预报中的预报结果,(b)订正面雨量在2012年流域水文预报中的预报结果 Fig. 9 Forecasts of area precipitation based on QPE1 in the 2012 river basin hydrological forecasts (a) original area precipitation, (b) corrected area precipitation |
| $ {\mathit{D}_\mathit{c}} = \frac{{{{\sum\limits_{\mathit{i} = 1}^\mathit{n} {\left[ {{\mathit{y}_\mathit{c}}\left(\mathit{i} \right) - {\mathit{y}_{\rm{0}}}\left(\mathit{i} \right)} \right]} }^2}}}{{\sum\limits_{\mathit{i} = 1}^\mathit{n} {{{\left[ {{\mathit{y}_\mathit{c}}\left(\mathit{i} \right) - {{\bar y}_{\rm{0}}}} \right]}^2}} }} $ |
式中,Dc为确定性系数,yc为预报流量,y0为观测流量,y0为平均流量。
从两次过程估测的整体效果上来看,均取得与实际流量过程较为吻合,2012年的确定性系数达到0.67,2013年也达到0.64;在洪峰与径流量的估测上,2012年径流量误差稍大一些,洪峰误差较小(9.3%),2013年的估测误差均小于20%。对比订正前后面雨量的应用效果,两者预报效果基本相近。究其原因,主要是大雨量级的面雨量计算订正前后基本无区别,小量级面雨量的改善不能对模拟起到决定性的作用。
5 结论及成果应用前景本文从满足水文气象服务的需求出发,对2012—2013年国家气象中心定量降水估测产品(QPE1) 进行检验评估,并首次与国家气象信息中心定量降水估测(QPE2) 进行了对比检验;运用递减平均法对QPE1进行订正,得到面向流域的QPE产品。在此基础上,建立了基于QPE的江河流域面雨量精细化计算方法,将面雨量产品应用于沂河临沂站以上流域的水文模拟试验。研究成果为开展水文气象服务工作提供了必要的理论基础和技术支撑。
(1) 针对国家级QPE产品进行适用性评估。融合自动站雨量计降水及卫星、雷达等反演的降水产品有效利用了地面观测和反演降水各自的优势,在降水量值和空间分布上均较为合理,对10 mm以下降水有较好的估测能力,降水值偏大的时候,估测效果明显下降。其次,该产品的估测降水值相比水文站观测降水整体呈偏小趋势。另外,在黄河流域、松花江流域及珠江等流域中,该产品的估测能力较好,其余流域次之。基于TS评分、漏估率、空估率、估测偏差BIAS、命中率等指标,融合自动站雨量计降水、卫星、雷达反演的降水产品估测评分效果普遍低于仅融合自动站雨量计降水、卫星反演的降水产品估测评分值。
(2) 针对国家气象中心QPE产品,运用“递减平均法”对2013年进行了订正试验,确定在不考虑2012年误差平均的基础上,采用0.8的订正系数时,订正效果相对较好,订正后2013年QPE误差平均绝对值和相对误差均有不同程度的减小,均方根误差有一定的增大。订正后,大雨以下量级的相对误差改善较为明显,而大雨以上量级效果改善不明显。对2012年的订正权重系数为0.7时,订正效果较优,对于连续性降水,订正后的QPE在降水的连续性和量值分布上都较订正前有明显的提高。但对于降水仅出现在24 h内的降水,订正效果并不明显
(3) 通过应用“基于QPE的江河流域面雨量精细化计算系统”,将QPE产品转化为适于水文气象服务的江河流域面雨量产品,在沂河临沂站以上流域的两次连续性降水过程开展水文模拟试验表明,两次过程均与实际流量过程较为吻合,但订正前后的效果并不明显,主要原因是大雨量级的面雨量计算订正效果较差,小量级面雨量改善并不能对水文模拟起到关键作用。
(4) 本研究是对国家级QPE产品的面向流域的运用开发,首次对比了两种QPE产品的性能。研究开发了基于QPE产品的江河流域面雨量精细化计算系统,实现了QPE在水文预报的应用,弥补了过去面雨量计算主要靠空间插值的多种不足。
陈丽娟, 张培群, 赵振国, 2005. 松嫩辽流域夏季面雨量预测因子探讨[J]. 应用气象学报, 16(5): 663-669. DOI:10.11898/1001-7313.20050513 |
程丛兰, 陈明轩, 王建捷, 等, 2013. 基于雷达外推临近预报和中尺度数值预报融合技术的短时定量降水预报试验[J]. 气象学报, 71(3): 397-415. DOI:10.11676/qxxb2013.041 |
方慈安, 潘志祥, 叶成志, 等, 2003. 几种流域面雨量计算方法的比较[J]. 气象, 28(7): 23-26. DOI:10.7519/j.issn.1000-0526.2003.07.005 |
管成功, 王克敏, 陈晓红, 2006. 2002—2005年T213数值降水预报产品分析检验[J]. 气象, 32(8): 70-76. DOI:10.7519/j.issn.1000-0526.2006.08.012 |
李俊, 支树林, 郭艳, 等, 2012. SWAN系统雷达定量降水估测产品在江西的应用[J]. 气象与减灾研究, 35(2): 61-66. |
李莉, 李应林, 田华, 等, 2011. T213全球集合预报系统性误差订正研究[J]. 气象, 37(1): 31-38. DOI:10.7519/j.issn.1000-0526.2011.01.004 |
刘静, 叶金印, 张晓红, 等, 2012. 2011年6—8月淮河流域面雨量预报检验[J]. 安徽农业科学, 40(36): 17698-17700. DOI:10.3969/j.issn.0517-6611.2012.36.097 |
吕晓娜, 牛淑贞, 袁春风, 等, 2013. SWAN中定量降水估测和预报产品的检验与误差分析[J]. 暴雨灾害, 32(2): 142-150. |
邱学兴, 王东勇, 陈宝峰, 2012. T639模式预报系统误差统计和订正方法研究[J]. 气象, 38(5): 526-532. DOI:10.7519/j.issn.1000-0526.2012.05.002 |
沈艳, 潘畅, 宇婧婧, 等, 2013. 中国区域小时降水量融合产品的质量评估[J]. 大气科学学报, 36(1): 37-46. |
田付友, 程明虎, 张亚萍, 等, 2010. 校准雨量计密度对雷达联合雨量计估测流域平均面雨量的影响[J]. 气象学报, 68(5): 718-730. |
王运生, 谢丙炎, 万方浩, 等, 2007. ROC曲线分析在评价入侵物种分布模型中的应用[J]. 生物多样性, 15(4): 365-372. |
肖丹, 邓莲堂, 陈静, 等, 2010. T213与T639资料驱动WRF的预报初步检验比较[J]. 暴雨灾害, 29(1): 20-29. |
徐晶, 林建, 姚学祥, 等, 2001. 七大江河流域面雨量计算方法及应用[J]. 气象, 27(11): 13-16. DOI:10.3969/j.issn.1000-0526.2001.11.003 |
徐晶, 姚学祥, 2007. 流域面雨量估算技术综述[J]. 气象, 33(7): 15-21. DOI:10.7519/j.issn.1000-0526.2007.07.002 |
翟丹华, 张亚萍, 邱鹏, 等, 2015. 琼江两次洪水过程的水文气象分析[J]. 气象, 41(1): 59-67. DOI:10.7522/j.issn.1000-0534.2013.00156 |
张国平, 赵琳娜, 许凤雯, 等, 2010. 基于流域结构分析的中国流域划分方案[J]. 北京师范大学学报(自然科学版), 46(3): 417-423. |
张亚萍, 程明虎, 徐慧, 等, 2007. 雷达定量测量降水在佛子岭流域径流模拟中的应用[J]. 应用气象学报, 18(3): 295-305. |
张亚萍, 张勇, 廖峻, 等, 2013. 天气雷达定量降水估测不同校准方法的比较与应用[J]. 气象, 39(7): 923-929. DOI:10.7519/j.issn.1000-0526.2013.07.013 |
赵琳娜, 吴昊, 田付友, 等, 2010. 基于TIGGE资料的流域概率性降水预报评估[J]. 气象, 36(7): 133-142. DOI:10.7519/j.issn.1000-0526.2010.07.020 |
 2016, Vol. 42
2016, Vol. 42