引言

数值预报已是世界各国开展业务天气预报最重要的途径之一，而资料观测及分析方法误差，模式误差以及大气系统本身的混沌特性使得单一确定性数值预报存在着不确定性。为解决单一数值模式预报存在的局限性，而发展出的考虑初始场不确定和模式不确定性的集合数值预报技术已成为当今数值预报领域的重要发展方向。就形成集合预报的扰动技术方案的基础而言，主要分为两种：一种对初值场进行扰动，来体现由于数值模式观测及分析场存在误差所造成的不确定性；二是模式扰动，来体现数值模式本身存在的不确定性。早期集合预报技术发展时，只使用初值扰动技术。仅采用初值扰动方法构建的集合预报系统存在着预报离散度偏小的问题，且不能表现出由于模式误差或模式本身缺陷而造成的误差(Houtekamer et al，1996, Buizza et al，1999; Ross et al, 2005)，因此完善的集合预报系统应同时包含初值扰动和模式扰动，以更好地表现预报的不确定性。

目前模式扰动方法主要有三类：(1) 通过在一个集合预报模式中采用不同的物理过程参数化方案来体现对模式物理过程描述上的不确定性(Houtekamer et al，1996)；(2) 采用多模式的方法来体现模式物理过程和动力过程的不确定性(Krishnamurti et al，2000; 2009)；(3) 在模式中引入随机参数化方案来体现大气运动方程数值求解过程中所存在的不确定性(Buizza et al，1999)，此外，这种方法基于由非线性噪音所激发的纠正功能的理论基础，从理论上还具有能减小模式系统误差的能力。因此，模式随机参数化技术的研究是近年来国际上集合预报系统扰动技术研究的重要方向，也是各大业务中心集合预报技术研发和改进的重要内容。

就集合预报系统中随机扰动技术的发展而言，Buizza等(1999)率先在ECMWF集合预报系统中开展了针对模式物理参数化过程的随机扰动方法研究，称为随机扰动参数化倾向方案(Stochastically Perturbed Parameterization Tendencies，SPPT)。Buizza等(1999)所使用的SPPT方案是在模式次网格尺度物理参数化总倾向项上乘一个分布在0.5~1.5的均匀分布的随机型，这种随机型在空间和时间结构上呈分段常数的特征，该方案的引入增加了ECMWF集合预报系统的离散度，提高了概率预报的技巧。此后，延续这种模式物理过程随机扰动技术的方向，一些学者相继开展了模式物理过程参数的随机扰动技术研究，如Lin等(2000)在模式循环中引入一阶自回归模式(马尔科夫过程)的随机过程，来扰动Betts-Miller对流参数化方案的有效位能。Li等(2008)在Lin等(2000)工作的基础上，对基于一阶自回归模式(马尔科夫过程)随机过程在空间上进行球谐函数展开(水平)和傅里叶展开(垂直方向)，使得所构造的随机型不仅随时间变化(相关)，且具有空间变化特征，并利用这种随机型进行区域集合预报系统中模式物理过程参数化方案中敏感参数的扰动试验。另外英国气象局全球集合预报系统中采用了随机扰动模式参数的方案。

Palmer等(2009)对ECMWF全球中期集合预报系统中的SPPT方案进行了改进，主要是改进了随机扰动型生成技术，将随机扰动场由原有的基于多变量的均匀分布特征，转变为单变量的高斯分布，并在空间上进行谱展开，使扰动模型在时间和空间上更为连续。这种随机扰动场的生成技术与Li等(2008)所采用的随空间和时间变化的随机扰动场类似。此外，在加拿大气象局全球集合预报系统中应用的SPPT方案中也采用类似的随机扰动场(Charron et al, 2010)。

除了SPPT方案扰动之外，还有两类模式随机扰动技术：一是随机动能后向散射方法(Stochastic Kinetic Energy Backscatter，SKEB)(Shutts，2005)，二是NCEP全球集合预报系统中采用的随机扰动模式总倾向项技术(Hou et al, 2008)。SKEB技术是针对数值模式动力框架在截断尺度存在的动力过度耗散的模式误差，通过SKEB来弥补被耗散的能量对可分辨尺度的影响。自2009年起欧洲中心集合预报系统同时使用SKEB和SPPT技术(Berner, 2009)，需要指出的是SKEB方案中所使用的随机场的产生技术与SPPT方案中的类似，也是具时空相关性。此外，英国气象局和加拿大气象局的全球集合预报系统也采用了SKEB方案。

国内集合预报模式扰动方法研究多采用多物理过程方法(陈静等，2003a; 2003b；谭燕等，2007; 2014；郝世峰等，2011)和多模式超级集合预报方法(智协飞等，2009; 2014;2015a;2015b；张涵斌等，2015；吴政谦等，2012；董海萍等，2013)。国内随机物理过程扰动方法的研究相对较少, 目前只有任志杰等(2011)和谭宁等(2013)对此做了研究，任志杰等(2011)和谭宁等(2013)在T213全球集合预报系统中开展了SPPT方案的应用研究，其中随机扰动场为变化范围在[0.5~1.5]均匀分布随机数, 随机场分布空间和时间上不相关。

中国气象局数值预报中心GRAPES_MEPS于2014年8月实现业务化运行，GRAPES_MEPS系统目前采用了多物理过程参数化(2个边界层参数化方案和3个积云对流参数化方案)的模式扰动技术，但GRAPES_MEPS仍存在集合离散度偏低，对强天气过程预报能力不足的问题。为进一步体现模式物理过程参数化所造成的不确定性，本研究将在GRAPES_MEPS中引入SPPT方案，其中SPPT方案中也采用具有时空变化特征的随机型[基于Li等（2008）工作]。在引入SPPT方案的基础上，开展SPPT方案中相关参数的敏感性试验，并且客观评估分析效果，此外，针对一次强天气过程，分析了有、无SPPT方案GRAPES_MEPS试验预报结果及其影响机理。期望上述工作能为GRAPES_MEPS的模式扰动技术升级提供科学依据。

1 GRAPES_MEPS系统简介

本文的研究工作将基于2014年8月业务化运行的GRAPES_MEPS设置，其中预报模式采用GRAPES_Meso-3.3.2.4版本，集合成员数为15(14个扰动成员+1个控制预报)，预报区域为中国大陆区域(15°~55°N、70°~135°E)，系统水平分辨率15 km，模式水平格点规模为502×330，垂直层为31层，预报时效为72 h。GRAPES_MEPS初值扰动技术采用集合变换卡尔曼滤波(Ensemble Transform Kalman Filter, ETKF)初值扰动技术(马旭林等，2008；Wang et al, 2008；张涵斌等，2014a; 2014b；Zhang et al, 2015a; 2015b;2015c)。在模式扰动技术方面，GRAPES_REPS采用了多参数化方法来体现模式物理过程参数化方案的预报不确定性，通过组合2个边界层参数化方案和3个积云对流参数化方案来构建不同集合成员的模式扰动方案。此外，GRAPES_MEPS区域集合预报系统还考虑了侧边界条件的不确定性，通过T639全球集合预报(15个成员)为GRAPES区域集合预报扰动成员提供相应的扰动侧边界条件。

2 SPPT方案介绍

GRAPES区域集合预报系统虽已采用多参数化方案的模式扰动技术，但存在着离散度不足的问题(张涵斌等，2014b)，本文将在GRAPES_REPS系统中引入SPPT方案，以期能改进和提高系统的离散度和预报技巧。SPPT方案的基本思想是对模式物理过程参数化方案的净倾向项X_C进行随机扰动，产生扰动的净倾向项X_P：

$ {X_P} = \psi {X_C} $

(1)

式中ψ为随机场。可以看出，SPPT方案实施的关键环节之一为合理的随机型产生方案，本文将参考Li等(2008)提出的随机型产生方案，这种随机型产生方案的基础是对基于一阶马尔科夫链随机过程(也称一阶自回归随机过程)，进行水平方向的球协函数展开，使随机场具有空间结构和时间相关特征。所定义的空间和时间相关的三维结构的随机场ψ(λ, φ, t)为：

$ \psi \left({\lambda, \phi, t} \right) = \mu + \sum\limits_{l = 1}^L {\sum\limits_{m = - l}^l {{\alpha _{l, m}}} } \left(t \right){Y_{l, m}}\left({\lambda, \phi } \right) $

(2)

式中, μ为平均值，α_{l, m}(t)为时间相关的随机场的谱系数，变量λ, φ, t分别表示经度、纬度和时间，Y_{l, m}为球协函数，l, m分别为水平方向总波数、纬向波数，L为随机场的水平截断尺度。随机场的谱系数α_{l, m}(t)的演变是通过一阶马尔科夫链的随机过程来实现随时间相关：

$ \begin{array}{l} {\alpha _{l, m}}\left({t + \Delta t} \right) = {e^{ - \Delta t/\tau }}{\alpha _{l, m}}\left(t \right) + \\ \sqrt {\frac{{4\pi {\sigma ^2}\left({1 - {e^{ - 2\Delta t/\tau }}} \right)}}{{L\left({L + 2} \right)}}{\rm{ }}} {R_{l, m}}(t) \end{array} $

(3)

式中，Δt是特定的时间间隔(在集合预报系统中，可以对应模式的积分步长，本文为300 s)，τ是随机场失相关的时间尺度。在本文中R_{l, m}(t)为服从方差为1，均值为0的高斯分布随机过程。进而可以得知，式(2) 中随机扰动场ψ(λ, φ, t)也具高斯分布特征，其平均值为μ。此外，式(3) 中的σ为随机扰动场ψ(λ, φ, t)为指定的标准差。

在式(2) 和式(3) 所定义的随机场ψ(λ, φ, t)基础上，引入一个拉伸函数S(ψ, μ)来实现产生用户能设定变化范围(给定上、下边界值)随机场，且能改变扰动场的PDF分布的随机扰动场Ψ (λ, φ, t)：

$ \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left({\lambda, \phi, t} \right) = \mu + S\left({\psi, \mu } \right)\left[ {\psi \left({\lambda, \phi, t} \right) - \mu } \right] $

(4)

本文中采用的拉伸函数S与Li等(2008)工作相同：

$ S\left( {\psi ,\mu } \right) = 2 - \frac{{1 - \exp \left[ {\beta {{\left( {\frac{{\psi - \mu }}{{{{\boldsymbol{\psi}} _{\max }} - \mu }}} \right)}^2}} \right]}}{{1 - \exp \left( \beta \right)}} $

(5)

这里β是常数，其值为-1.27, μ=(Ψ_max+Ψ_min)/2, 其中Ψ_max，Ψ_min分别代表随机场Ψ (λ, φ, t)的上，下边界。以产生在[0.5~1.5]之间，均值为1的随机数为例，通过指定上述边界值，和均值就能通过经过式(4) 中经过拉伸函数处理后的Ψ来产生，且Ψ函数对应PDF分布特征也较未拉伸前ψ的PDF(其均值也为1) 更宽，使得随机场在指定范围内变化更为均匀。

在本研究中，首先在GRAPES_Meso模式中引入前文所述的随机场Ψ (λ, φ, t)产生器，进而将随机数乘到GRAPES_Meso模式中物理过程参数化方案产生的净倾向项上来具体实现SPPT方案，目前是对T，U，V，Q四个预报变量的净倾向项进行扰动。

ECMWF全球集合预报系统中原有SPPT方案(Buizza et al，1999)及升级的SPPT方案(Palmer et al，2009)扰动随机数的取值范围为[0.5, 1.5]，加拿大全球集合预报系统中SPPT方案(Charron et al, 2010)中随机扰动场取值范围也设置为[0.5, 1.5]，扰动场的均值为1。由于不同的预报系统之间有较大的差异，上述扰动范围是否适合我国GRAPES区域集合预报系统，还需要进行试验分析。

3 SPPT方案中随机扰动振幅变化影响试验及检验

在开展引入SPPT方案的GRAPES_MEPS集合预报试验时，首先进行的是国外业务中心通用的随机扰动场取值范围为[0.5, 1.5]的试验(即表 1中的试验SPPT_P1)，通过连续试验的客观检验发现，采用此取值范围随机场的SPPT方案对GRAPES集合预报系统性能改进有正效果，但是不显著(下文将详叙)。为此本文开展了三组使用不同随机场扰动幅度(均值为1) 的SPPT方案的集合预报试验，以期找出与适合GRAPES_Meso模式系统SPPT方案的随机扰动参数变化范围，SPPT方案差异的具体细节见表 1。另外，将未使用SPPT方案的集合试验作为参考系统(试验名为noSPPT)。这四组试验的初值扰动为GRAPES_MEPS业务系统中产生的基于ETKF技术的扰动初值，扰动的侧边界是来自T639全球集合预报系统，在本组试验中，随机扰动场的时间失相关尺度取为1 h。

试验时段为2014年8月4—15日(总计12 d)，试验积分起始时间是每日12 UTC，试验预报时效为72 h，模式预报结果输出间隔为3 h。

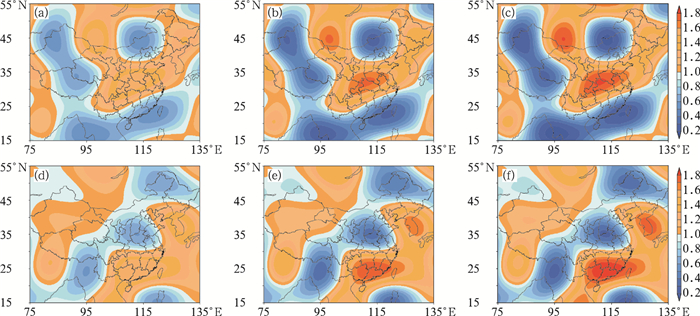
3.1 SPPT随机函数范围敏感性试验的扰动场分析

图 1给出SPPT_P1、SPPT_P2、SPPT_P3试验中同一集合成员在不同预报时效对应的随机扰动结构(以2014年8月6日试验的集合成员5在12和42 h预报为例)，可以看出，在同一个时次，这三组试验的随机扰动场空间分布特征是相同的，仅扰动值的振幅大小有差异，此外，通过对比不同时次的扰动场结构可以看出，本研究采用的扰动场具有随时间变化的特征。

3.2 集合预报统计检验

本文采用如下集合预报检验指标：集合离散度(spread)和集合平均均方根误差(ensemble mean RMSE)关系；连续分级概率评分(continuous ranked probability score，CRPS)；outlier评分及相对作用特征面积(area under relative operating characteristic curve，AROC)等对上述四个试验的结果进行客观检验，以较全面地评估集合预报试验在可靠性，预报分辨率能力上的差别。检验时所用的分析场为GRAPES_Meso模式自身的分析场。

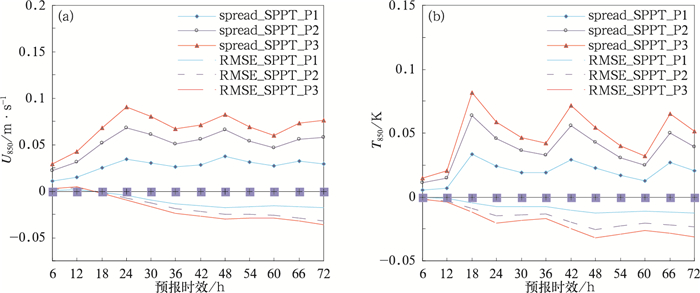
集合离散度体现的是集合预报各成员的离散程度, 其发散程度在一定范围内越大越能体现预报的不确定性，集合平均误差(RMSE)是比较集合平均与观测值之间的差异，用来衡量集合预报误差大小。理想的集合预报系统，其集合离散度和集合平均误差是越接近越好，即离散度能代表系统的误差演变特征，系统的可靠性高。因此，分析其两者之间的关系是检验集合预报系统是否可靠的重要指标之一。图 2给出的是试验期间三组使用不同随机扰动幅度SPPT方案的集合预报试验温度和风场预报的集合离散度、集合平均均方根误差与无SPPT方案试验的对应结果差值的时间演变。由图 2a和2b看出，对于850 hPa温度和风场，三组SPPT方案试验的集合离散度的差值都是正值，而集合平均均方根误差的差值都是负值，说明SPPT方案有助于提高GRAPES_MEPS集合离散度，且降低系统的预报误差。但对比而言，无论是温度场还是风分量，采用随机扰动场振幅在[0.5, 1.5]的SPPT_P1试验的离散度改进及误差降低程度最小，而随机扰动幅度最大的SPPT_P3试验的离散度提高和误差减小最为显著，处在中间扰动幅度的SPPT_P2的结果在上述两个试验之间。对于其余各层的温度和U风分量(图略)也可以得出类似的结论。进一步分析，SPPT_P3试验中集合平均误差的差值的演变可以看出，随模式积分时效增加，采用适当随机场参数的SPPT方案对系统误差改进是不断增大的。

由上试验结果可知，就GRAPES_Meso模式系统而言，需要采用较大幅度的扰动SPPT方案来体现模式物理过程参数化方案的不确定性。采用扰动幅度较大SPPT方案，能改进GRAPES_MEPS的离散度，并能降低系统的均方根误差，尤其是在积分中后期，均方根误差得到了较为明显的改善，从而使集合离散度和集合平均误差关系更为接近，改善了GRAPES_MEPS系统的可靠性。

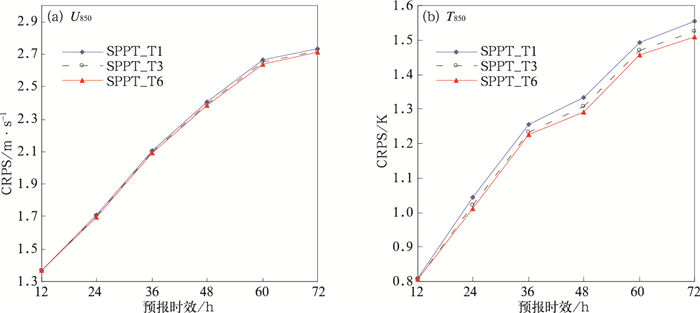
连续分级概率评分(CRPS)是一种检验集合预报系统概率预报技巧的综合评分，其具有与被检验变量相同的单位，可客观定量检验预报的准确性。CRPS值越小，预报准确性越高。图 3a和3b给出的是各组试验中850 hPa等压面层上温度和U风的CRPS评分的演变。可以看出，对于850 hPa等压面的U风预报(图 3a)，三组采用不同扰动幅度的SPPT方案的试验的CRPS评分差异不明显，略低于无SPPT方案试验，但相比而言，采用大扰动幅度SPPT方案的SPPT_P3的CRPS评分最小。另外，三组使用SPPT方案的试验对850 hPa温度的预报(图 3b)技巧有一定程度的改进，其中SPPT_P3试验的改进最显著，且随着积分时间的延长而增加(T850 CRPS在积分后期改善明显)，SPPT_P2试验次之，扰动幅度最小的SPPT_P1试验的改进最小。

就SPPT方案对集合预报系统预报技巧的影响而言，CPRS评分的检验结果与前文中讨论过的SPPT方案对GRAPES_MEPS集合离散度和集合平均误差关系影响的结果基本类似，即SPPT方案对等压面要素预报技巧有正贡献，但采用较大幅度扰动SPPT方案试验的预报技巧改进更为显著，且SPPT方案的正效果随着预报时效延长而增强。

outlier评分是由Talagrand直方图进一步发展出的评分，是计算观测值落在Talagrand直方图中最两端的两个盒子(bins)中的频率，即观测落在集合成员的预报区间之外的频率，以表示集合预报系统的漏报率。outlier评分也是评估集合预报系统可靠性指标之一，outlier值越小，则观测值落在预报区间外的概率越低，漏报率就低，系统就越可靠。

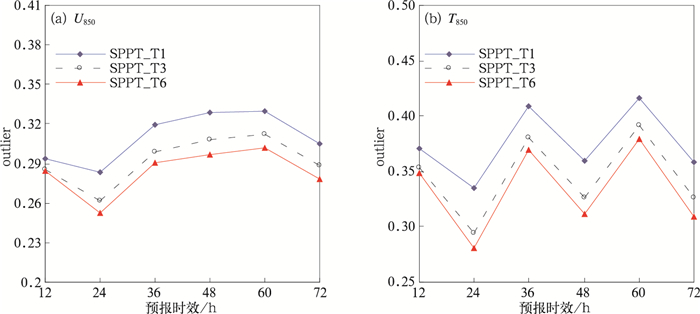
图 3c和3d分别给出了四组试验850 hPa温度和纬向U风的outlier评分演变。可以看出，相对于无SPPT方案的试验，三组使用SPPT方案的试验均能降低两个等压面层上温度和U风预报的漏报率，其中采用随机扰动幅度最大的SPPT_P3试验的outlier评分减小最显著，减小幅度在2%~6%，其次是SPPT_P2，再次是SPPT_P1。

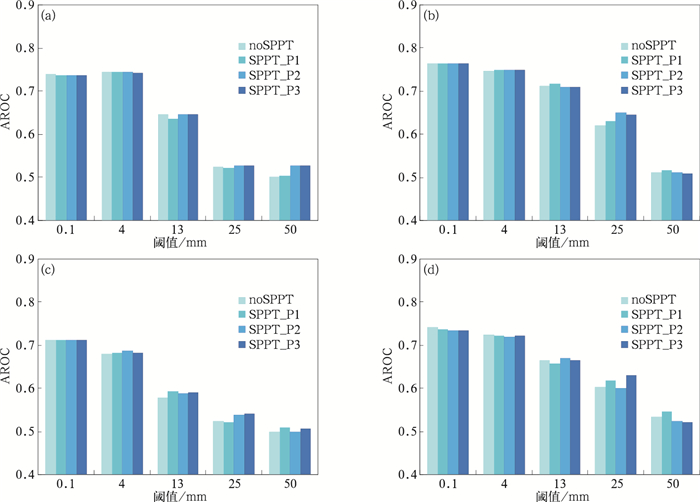
3.3 降水检验

本文也检验了试验期间四组集合预报试验降水预报的概率预报技巧。图 4给出的是这些试验针对不同降水阈值的逐6 h累计降水的AROC评分。AROC评分能够给出集合预报系统对特定阈值事件的辨别能力的信息，AROC评分值越大，表示预报分辨能力越高。从不同预报时效的6 h累计降水来看，在各个预报时效对于小雨和中雨量级降水，采用SPPT方案三个试验，与无SPPT方案试验的AROC评分差异较小，在中到大雨量级[25 mm·(6 h)^-1以上]降水预报上，有SPPT方案试验的AROC评分一定程度的提高，比如在12~24 h预报时段中，SPPT_P3试验中50 mm阈值降水, 以及42~48 h和54~60 h预报时段中，SPPT_P3试验中25 mm阈值降水AROC值明显高于无SPPT方案扰动试验。同时，我们也注意到，较大扰动幅度SPPT方案两组试验SPPT_P2和SPPT_P3对于降水能力似乎相当。由于降水检验是在站点上进行检验，统计样本数要远小于等压面上的格点检验，因此，还需要开展更长时间的试验来进一步验证。

基于上述试验结果，采用随机扰动幅度较大的SPPT能较显著地改进GRAPES_MEPS等压面温度和风预报的集合离散度，也可一定程度减小降低预报误差，为进一步测试SPPT方案中随机扰动场的变化幅度，本研究还开展了采用均值为1，随机扰动场在[0.1, 1.9]以及均值为1.5，随机扰动场在[0.5, 2.5]的SPPT方案的GRAPES_MEPS试验(图略)，发现随机扰动振幅为[0.1, 1.9]这组试验的检验结果与扰动振幅为[0.2, 1.8]的试验的结果类似，而随机扰动场振幅为[0.5, 2.5]这组试验中集合离散度虽有增加，但集合平均误差也大幅上升，甚至超过控制预报的均方根误差。因此，SPPT方案中所乘在物理过程参数化净倾向项的随机数均值需为1，极限值为[0.1, 1.9]。

4 SPPT方案中随机型时间尺度的影响

前文提到，本研究SPPT方案采用随时间变化的随机型Ψ (λ, φ, t)，影响其变化频率的失相关时间尺度τ在上述三组改变随机场扰动幅度SPPT试验中设定为1 h。Charron等(2010)在加拿大全球集合预报系统中设定SPPT方案中随机型的失时间相关τ为3 h，且指出其改变对全球集合预报系统的影响不明显。自2010年起ECWMF集合预报系统中SPPT方案采用多空间和多时间尺度随机型，即在模式积分不同预报时效上利用预定对应的不同空间及时间尺度随机型进行SPPT方案扰动。可见，对于不同的集合预报系统(主要是模式)，SPPT方案所采用随时间改变随机型的更新频率对集合预报系统预报性能的影响效果是不同的，需要根据特定模式系统进行针对性的试验和评估。就本研究SPPT方案中所采用的随机型[见式(2) 和式(3)]而言，值大，意味两个时次之间随机场相关性就大，随时间变化频率就低。因此，针对GRAPES_MEPS，改变SPPT方案随机扰动场时间尺度参数是否会对集合预报结果造成影响呢？本文将对此进行多组对比试验。

本文基于上述试验的结果，选定SPPT_P3方案的[0.2, 1.8]作为扰动范围，将随机函数谱系数去相关时间尺度τ分别设置为1、3、6 h，进行了三组集合预报试验。

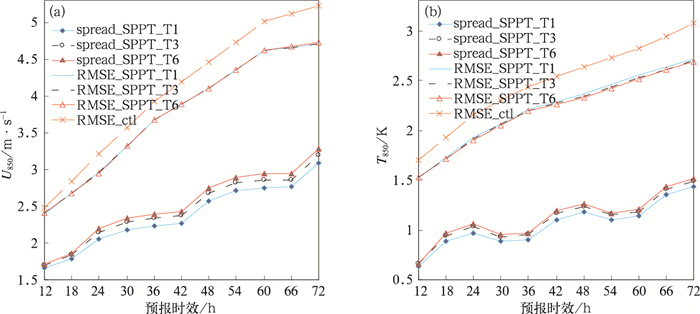
图 5为SPPT_T1，SPPT_T3和SPPT_T6三组试验中850 hPa纬向风和温度预报的集合平均均方根误差、集合离散度和随预报时效的演变。可以看出，三组试验中U₈₅₀(图 5a)集合平均均方根误差的差异很小，就集合离散度而言，在预报初期，各试验的差异较大，随着积分时效的延长，采用6 h失相关时间尺度的SPPT_T6试验中U₈₅₀的集合离散度增长最快，其次是SPPT_T3试验，最小为SPPT_T1试验。温度场的结果与纬向风的结果类似，此外，SPPT_T6试验中温度集合平均误差也略小于其他试验。

图 6是三组试验850 hPa纬向风和温度预报的CRPS评分。对于风场预报CRPS评分(图 6a)，三组试验的预报技巧基本相同，没有明显差别，而使用不同时间尺度扰动SPPT方案试验对温度场预报技巧的影响似乎较为明显，其中SPPT_T6试验的CRPS评分值最小，SPPT_T3试验次之，SPPT_T1最大。同时，也可以观测到SPPT_T6和SPPT_T1试验的CRPS评分的差异随时间积分是增大的。

图 7为三组试验850 hPa纬向风和温度预报的outlier评分，其中SPPT_T6试验中的U₈₅₀(图 7a)和T₈₅₀(图 7b)outlier评分值最小，其次是SPPT_T3试验，最大为SPPT_T1试验。SPPT_T6和SPPT_T1试验之间的漏报率差异很显著，最大可达5%。结合前节比较不同扰动幅度试验中，SPPT_T1试验相对于未使用SPPT试验的2%~6%的漏报率降低幅度，可以得出相对于无SPPT方案试验，SPPT_T6试验能降低漏报率达7%左右。

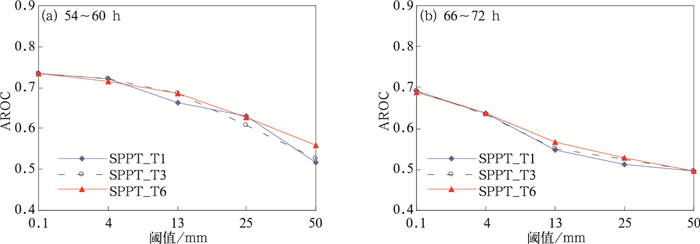
另外，本研究也进行了上述三组试验预报后期逐6 h累计降水的AROC概率评分(图 8)。可以看出，对于小雨量级的降水，三组试验的预报技巧没有明显的区别，对于13 mm·(6 h)^-1以上降水，SPPT_T3和SPPT_T6试验的AROC值为0.686，高于SPPT_T1试验的0.664；对大于25和50 mm·(6 h)^-1量级的强降水而言，SPPT_T6的预报技巧最高。类似的结果也可见66~72 h的降水结果，对于中雨以上量级，SPPT_T6试验的预报分辨能力最高。

由上可知，GRAPES_MEPS中SPPT方案的应用效果对随机扰动场的失相关时间尺度的选择也比较敏感，本研究中的试验结果表明，采用较大随机扰动幅度([0.2, 1.8])，及较长的失相关时间尺度(6 h)的SPPT方案能显著改进系统的离散度，降低漏报率，且在一定程度上改进系统对中到大雨的预报技巧。本试验选取的时间尺度参数是国际上常用取值，对于更大的时间尺度参数是否会进一步优化GRAPES_MEPS的预报效果，还有待于更多试验去验证。

5 应用SPPT方案的GRAPES_MEPS典型降水个例分析

前文试验及客观统计结果显示，适合GRAPES_MEPS的SPPT方案能改进中到大雨量级降水的预报技巧。本文进一步以2014年8月6日12—18时一次强降水过程为试验个例，分析使用SPPT_T6方案的GRAPES_MEPS试验的降水预报结果。集合预报从2014年8月6日12 UTC起报，积分72 h。图 9是此次降水过程6 h降水量的实况图，降水发生在湖北西南部以及湖南北部地区，局地性较强。最大降水中心出现在湖北省宜昌市，中心雨量>80 mm。

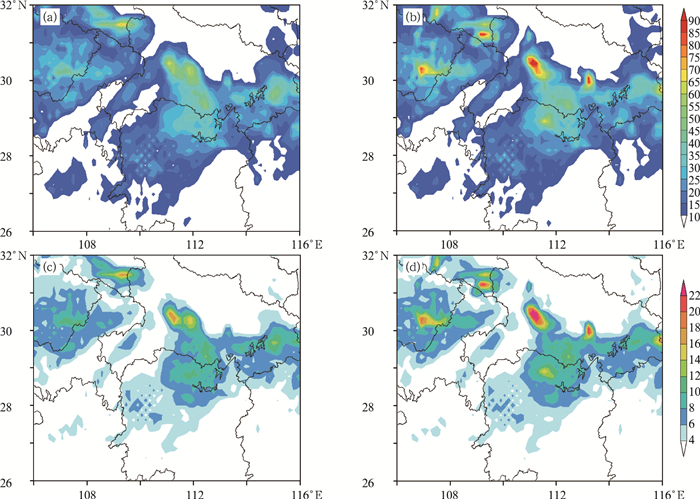
图 10为无SPPT方案及SPPT_T6集合预报试验预报的对应时段的最大降水量和集合离散度。可以看出, 两个试验预报的降水区域范围基本一致，但对强降水落区中心的量级预报存在明显的差异(图 10a，10b)，SPPT试验预报中各降水中心的降水量级均大于无SPPT方案。无SPPT方案试验在宜昌附近的最大降水量预报明显低于实况降水量，而SPPT试验在小雨量级降水预报基本不变的前提下，而SPPT_T6试验中的最大降水量在宜昌附近达到了80 mm，和实况量级非常接近。以上说明SPPT方案能较明显地改进GRAPES_MEPS对大雨量级预报偏低的情况。此外，对比两个试验的降水集合离散度发现，SPPT_T6试验在宜昌地区的集合离散度明显大于无SPPT方案试验(图 10c，10d)，说明该地区的降水预报具有很强的不确定性。

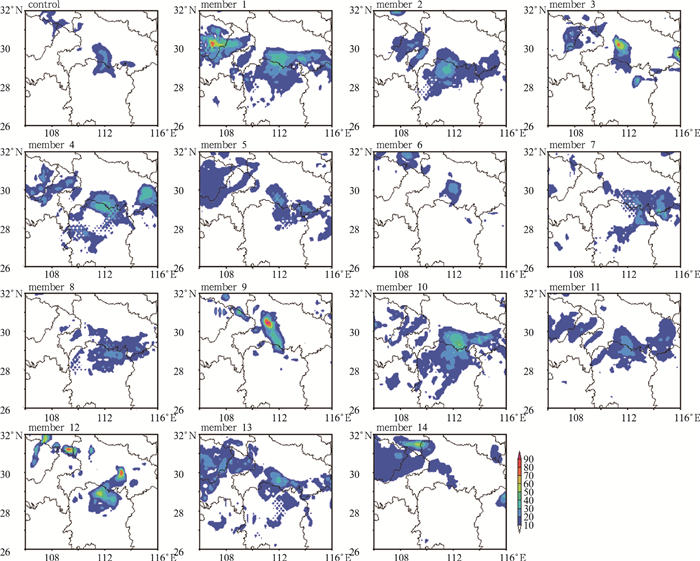
图 11是SPPT_T6试验预报的强降水发生期间的6 h累计降水邮票图。可以看出，成员3和成员9较准确地预报出了此次过程降水中心的落区和量级，尤其是成员9，对降水量级的预报十分接近于实况，但不同的集合成员的预报结果有明显的差异，各成员之间对降水落区的预报比较发散，对比分析无SPPT方案试验的邮票图(图略)发现，SPPT方案对于降水落区的影响不大，两个试验的降水预报范围非常接近，但在无SPPT方案试验的降水量明显偏小于实况。GRAPES_MEPS在这次降水过程中各成员之间预报的差异性，可能与还采用的多物理过程参数化方法，及来自T639全球集合预报系统的侧边界扰动差异大有关。此外，本文还进一步分析了对应强降水中心(实况的大值格点)，无SPPT方案试验和SPPT_T6试验中成员9预报的逐小时降水量(图 12)，由于模式预报的降水中心相对实况有少许偏移，因此对应的预报值偏小，但仍可以看出，SPPT_T6试验降水量在降水发生的第4、5、6 h明显比无SPPT方案试验高1~2 mm，更接近于实况。

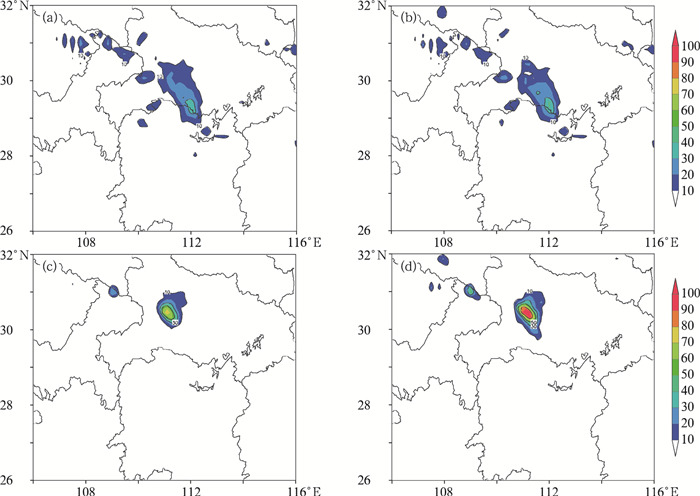
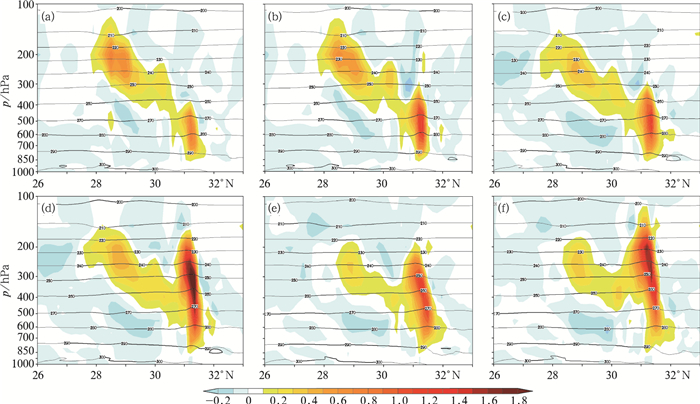
在此，我们进一步分析SPPT方案在改进GRAPES_MEPS对此次降水预报中的作用及影响机制，图 13较准确预报出降水落区和量级的集合成员9的大尺度格点降水和次网格尺度降水量，可以看出，引入SPPT方案后，格点尺度的降水并没有明显的变化，而次网格尺度的降水有了明显的差异，在最大降水中心，SPPT扰动的次网格尺度降水量明显高于无SPPT试验。图 14为有、无SPPT方案试验在8月6日16、17、18时的垂直速度和温度沿降水中心度的经向(111°E)垂直剖面图。在降水的前3 h，两个试验的垂直速度和温度预报并无太大差异(图略), 从降水的第四个小时(即6日16时，图 14a, 14b)开始, 宜昌(31°N)上空SPPT试验的温度脊略微向上延伸, 垂直速度开始加强, 到17时(图 14c和14d)和18时(图 14e和14f), SPPT试验中温度脊较无SPPT试验明显向上延伸，不稳定能量加强，垂直速度增大且对流更加深厚，进而产生较强降水量。作为对前文客观统计结果中SPPT能改进GRAPES_MEPS对中至大雨量级降水能力的补充，上述个例过程分析说明，对于弱天气系统影响下的强天气过程，采用SPPT方案可以一定程度上体现其预报不确定性，通过对物理过参数化所影响的次网格尺度运动进行合理随机扰动，能一定程度改进集合预报系统对强降水过程的预报能力。

6 结论与讨论

为进一步改进和提高GRAPES_MEPS的模式扰动技术，本研究首先在GRAPES_MEPS引入了SPPT方案，针对每个集合成员，对其预报模式(GRAPES_Meso)物理过程参数化的净倾向进行随机扰动。所采用SPPT方案中的随机型为基于一阶马尔科夫链谱系数展开，其统计特征服从高斯分布特征，也具有空间结构和时间相关特征(国际各大业务中心集合预报系统中SPPT方案也采用此类随机型)。

据国外业务中心集合预报系统SPPT方案的应用经验，SPPT方案中扰动随机扰动场参数设置(如扰动空间尺度、时间相关尺度)因模式系统的不同而异，需根据自身模式特点进行试验设定。因此，本文进一步开展了SPPT方案中随机场的扰动幅度和失时间相关尺度等参数优化设置的敏感性试验，并进行了较全面的集合预报客观检验。通过上述试验，确定了适用于GRAPES_MEPS的SPPT方案中随机扰动场的优化参数设置，即采用较大随机扰动幅度([0.2, 1.8]，均值为1)，及6 h失相关时间尺度的随机型。同时，集合试验的客观统计检验结果还表明，采用优化参数设置的SPPT方案能改进GRAPES_MEPS对等压面上要素如温度和风场等预报技巧(小的CRPS评分)，改进了其预报的可靠性，具体表现为提高集合离散度，且在一定程度上降低集合平均误差，同时也降低了其预报漏报率，同时，还能在一定程度上改进中到大雨的预报技巧。值得一提的是，SPPT方案的作用在预报积分后期更为显著。

此外，针对一次强降水过程，分析了采用优化参数的SPPT方案GRAPES_MEPS试验预报结果及其影响机理，发现SPPT方案虽然对降水落区的预报没有显著影响，但能改善某些成员降水预报量级较小的问题，其影响作用是通过影响降水地区上空温度和垂直速度的差异，提高了降水大值中心次网格尺度降水的降水量，进而提高了对大雨量级降水的预报能力。

本文上述的试验结论虽是基于较短的连续试验期间(12 d)，但本文中相关结论，与2015年底数值预报中心所开展的包括SPPT方案的业务GRAPES区域集合预报系统技术升级而开展的1个月时段连续试验(2015年6—7月的夏季一个月)的结果是一致的。这次GRAPES_MEPS技术升级采用了本文试验确定出的优选参数设置SPPT方案(扰动幅度([0.2, 1.8]，均值为1)，及6 h失相关时间尺度)，连续试验结果表明，使用基于优化参数的SPPT方案确能有效改进业务GRAPES区域集合预报系统的离散度，降低漏报率，及提高对较强降水量级的预报技巧。