2. 江苏省气象探测中心, 南京 210009
2. Jiangsu Meteorological Observation Center, Nanjing 210009
在天气雷达探测中,阵风锋表现为位于雷暴前沿、出流边界、弓形回波、飑线强回波带的前沿一条或多条呈弧形的加强窄带回波。当它过境时,常伴有气压增高、气温降低和风向突变及风速急变,锋后有明显的地面辐散(Bedard et al, 1977)。我国新一代天气雷达采用5~6 min的体积扫描模式进行观测,可有效监测阵风锋等中小尺度天气系统产生、发展、成熟和消亡的全过程,揭示它们的产生条件和演变规律(李柏等, 2013)。阵风锋回波特征分析研究、机理研究、与其他天气系统的相互作用研究等越来越受到气象学者关注(吴芳芳等, 2009; 袁子鹏等,2011; 俞小鼎,2012; 张涛等,2013;王婷婷等,2011;席宝珠等,2015)。有关阵风锋的研究分析工作几乎遍及中国大部分地区,阵风锋往往伴随重大灾害性天气发生,因此阵风锋特征识别预警研究,对完善灾害性天气短时临近预警预报系统显得很有必要。
美国早在20世纪70年代就开展对阵风锋的研究,80年代由麻省理工学院林肯实验室提出基于天气雷达的阵风锋识别算法MIGFA(Machine Intelligence Gust Front Algorithm)(Uyeda et al,1986),目前已经发展到第三代,用于美国联邦航空管理局低层风切变探测。该算法以雷达数据为基础,利用多维图像处理、数据融合、模糊逻辑等技术来进行阵风锋自动识别。并且以MIGFA算法为基础的各种改进工作还在继续(Hermes et al, 1993; Crook et al, 2004)。该系统改进后推广至美国新一代天气雷达(NEXRAD)算法平台(Smally et al, 2005)。
随着我国新一代天气雷达网(CINRAD)建设的日趋完善,对中小尺度天气系统捕捉能力的大幅度提高,阵风锋等中小尺度系统的识别算法研发技术引起了研究人员关注。陈钢(2009)提出了在频域找阵风锋弓形回波区域区别于其他区域的独特形状特征算法,但该算法仅基于形状,识别效率较低。程浩等(2011)和何红红等(2013)利用熵函式模板和组合切变来识别阵风锋,但对于切变特征不明显的阵风锋无法识别。郑佳峰等(2013)通过双向梯度法和径向辐合线的综合方法实现了识别CINRAD/SB型号雷达探测到的低仰角阵风锋。由于阵风锋回波“窄带”和“强度弱”的特征,任何一种算法做推广时都需要针对当地阵风锋数据特征做相应调整。例如,CINRAD/SA型号天气雷达低仰角存在较严重的距离折叠现象,易遮挡径向速度PPI中小尺度特征,因此依赖径向速度数据的阵风锋识别算法识别率较低。李劲等(2011)以雷达反射率数据为主,根据合肥雷达探测到的阵风锋细线特征设计的函数模板实现了对江淮地区阵风锋特征的有效识别,但该算法没有考虑阵风锋快速移动、阵风锋高度与距离关系等特点,适用范围有限。
MIGFA算法发展至今已有30多年,它主要利用了阵风锋细线、移动和速度辐合三种特征。在数据质量控制、函数模板设计等诸多方面都具有无可比拟的优越性。因此本文针对江苏沿江天气雷达数据特征和该区域阵风锋特征,基于MIGFA算法,以反射率数据为主,考虑阵风锋细线、移动、阵风锋高度与距离关系等特点,根据本地阵风锋特征统计结果,综合0.5°、1.5°、2.4°及时间差分反射率阵风锋数据特征,调整、改进该算法中的阈值、函数模板,设计动态权重方案提高综合有效得分值。最后考虑阵风锋弧度和强度分布的特点,通过弧度判断和反射率平坦度测试排除其他窄带回波,进一步提高阵风锋识别效率。
1 基于MIGFA算法的改进 1.1 MIGFA算法简介MIGFA机器智能阵风锋算法来源于林肯实验室设计用于自动识别雷达图像上军用车辆的一种基于知识库的信号处理和对象识别技术。该方法采用前后关系知识、时空变化信息、数据融合、模糊逻辑、延迟阈值等技术来提高识别效果(Delanoy et al, 1993)。后用于识别美国机场的ASR-9 WSP和TDWR雷达的阵风锋特征。该套系统还推广至美国新一代天气雷达(NEXRAD)算法平台。由于不同型号的雷达信号处理、扫描方式、数据质量等均不一样,呈现的阵风锋特征也不完全一致。因此当算法移植到新雷达时,需要针对新雷达的数据特征做算法的调整和改进。例如MIGFA在针对ASR-9型号雷达较弱的敏感度、晴空下速度数据的可靠性较差等问题在数据质量控制方法上做了较多调整(Troxel et al, 2002)。移植到美国新一代天气雷达时对多种函数模板也做了相应调整和改进(Smally et al, 2005)。目前我国部分机场也采用该系统。但是该算法以在美国天气雷达捕捉到的阵风锋为依据,完全移植到我国易出现误判。因此若要提高该算法移植后的识别率,需要在充分熟悉本地天气雷达数据特征和该雷达探测到的阵风锋特征的基础上,对算法做进一步的调整和改进。
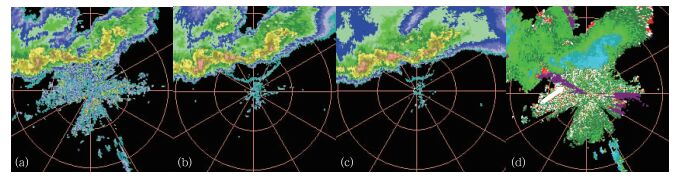
1.2 江苏沿江阵风锋特征在雷达图像中的表现华东沿海、沿江地区常年灾害性天气较多,尤其暴雨、短时强降水、雷雨大风等,给人民生命、财产带来较大影响。为更好地监测天气变化,该区域大部分雷达台站布设了10 cm波长的天气雷达,以CINRAD/SA型号为主。CINRAD/SA型号天气雷达由于较高的发射功率和灵敏度,其对弱降水和晴空大气有较强的监测能力,从而更能捕捉到阵风锋特征。不仅在0.5°仰角上,1.5°、2.4°仰角的反射率图像上也能清楚地观测到阵风锋细线特征(图 1),并且由于抬高仰角后杂波干扰大幅度减少,近雷达站区域更易观测到阵风锋细线特征。但由于CINRAD/SA天气雷达低仰角采用高低脉冲重复频率分离扫描方式,采用高重复频率测速时, 会有距离折叠现象出现, 当出现两者强度值相当时, 无法确定测速值(在图像上设置为紫色) (李柏等, 2013)(如图 1d白色箭头所示)。有些依赖速度数据的产品可以通过抬高仰角,或采用质量控制(徐芬等, 2007)和填补的方式(夏文梅等, 2011)来进行数据处理,但由于阵风锋小尺度特点,目前无有效手段去除(减弱)距离折叠影响,MIGFA算法中依赖速度辐合特征的识别技术较难实现,因此利用CINRAD/SA型号天气雷达数据进行阵风锋特征统计及识别工作,应以多仰角反射率数据为主。
|
图 1 阵风锋雷达图像 (a)0.5°反射率图像,(b)1.5°反射率图像,(c)2.4°反射率图像,(d)0.5°径向速度图像 Fig. 1 The gust front in radar image (a) 0.5°ZPPI image, (b) 1.5°ZPPI image, (c) 2.4°ZPPI image, (d) 0.5°VPPI image |
江苏沿江地区阵风锋在反射率因子图像上的总体特征和其他学者观测研究结果类似:表现为一条狭长的窄带回波,呈弧线状,垂直高度3 km以下,大部分窄带回波中心区域回波数值较其边缘两侧回波有所增高,即存在双梯度现象,MIGFA算法通过函数模板的设计表现这一特征,郑佳峰等(2013)通过计算每个回波点的双向梯度来保留线状的回波。但也存在一些差异,沿江地区阵风锋在0.5°仰角上回波强度一般在0~21 dBz;宽度在5~13 km,较高仰角(1.5°、2.4°)回波强度略高1~3 dBz,宽度在2~10 km,这与江淮地区的阵风锋反射率因子强度15~35 dBz,窄带回波宽度2~5 km略有不同(李劲等, 2011);郑佳峰等(2013)以河南、四川等地的CINRAD/SB天气雷达为主的阵风锋统计特征结果认为窄带回波强度值为5~30 dBz,宽度2~10 km。由此可见,由于地域、天气雷达型号、探测性能、扫描方式等存在差异,阵风锋特征相应也出现观测差异。尽管特征值相差不大,但对依赖特征阈值的算法来说,阈值较宽,会丢失阵风锋;阈值较窄,识别率将大幅度下降。因此要成功识别阵风锋,本地化属性要明确。
根据上述江苏沿江地区雷达基数据特征和该区域阵风锋在反射率图像上的特征,本文基于MIGFA算法,考虑阵风锋细线、移动、阵风锋高度与距离关系等特征,综合0.5°、1.5°、2.4°反射率数据及时间差分反射率数据,调整、改进算法中的阈值、函数模板,设计动态权重方案提高综合有效得分值。最后考虑阵风锋弧度和强度分布的特点,通过角度判断和反射率平坦度测试进一步降低虚警率,从而达到提高识别率的目的。
1.3 数据预处理 1.3.1 平滑的考虑基于阵风锋“弱”这一特征,在做数据预处理时应尽可能降低噪声,保持(突显)阵风锋细线特征。在预处理工作中平滑数据为主流做法,但在算法测试中发现,由于0.5°仰角反射率数据杂波干扰较为严重,阵风锋回波附近区域地物杂波等较多时,平滑处理后阵风锋细线特征易被“丢失”。因此为保证阵风锋特征的完整性,对反射率数据场进行预处理时,0.5°仰角数据不采取平滑措施。
1.3.2 低仰角数据的融合参考MIGFA算法移植至NEXRAD雷达时做法,为提高近雷达站低仰角数据质量,减少异常传播回波和地物杂波的干扰,0.5°仰角数据预处理时采用了数据融合,做法如下:1~20 km采用1.5°仰角反射率数据;20~25 km线性融合0.5°和1.5°两层数据;25~150 km 0.5°仰角数据保持不变。
1.4 函数模板的改进与设计MIGFA算法识别成功的关键是多种函数模板的设计,在原算法中设计了低仰角反射率阵风锋细线函数模板、放射状回波函数模板、时间差分反射率阵风锋细线函数模板、空间差分反射率阵风锋细线函数模板、风暴边缘函数模板等用来提取相应特征。这些函数模板的设计及阈值定义均基于相应数据特征。例如在移植至NEXRAD雷达产品系统时对多种函数模板均进行了调整(Smally et al, 2005)。因此本文针对1.2节江苏沿江地区天气雷达数据特点及阵风锋数据特征,对0.5°反射率回波阵风锋细线函数模板进行了改进,并增加设计了较高仰角反射率回波阵风锋细线函数模板。
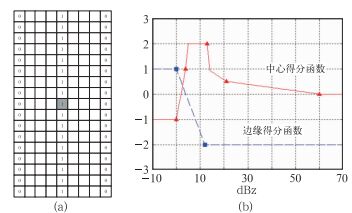
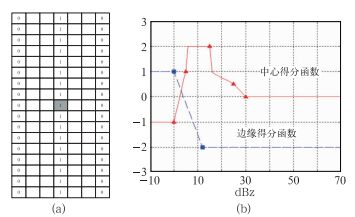
1.4.1 低仰角阵风锋细线函数模板改进根据江苏沿江低仰角(0.5°)阵风锋细线特征,细线模板调整为如图 2a所示,默认宽度设为9个像素。长度与原算法一致。中心区域(图 2a“1”所在网格)得分函数对应图 2b红色线段;边缘区域(图 2a“0”所在网格)得分函数对应图 2b蓝色线段。函数线段与原算法相似,阈值有所调整。根据阵风锋中心值特点,给予4~13 dBz高得分值。该函数模板的设计也体现了阵风锋窄带回波另一个特点:双梯度,即窄带中心回波值较高,而边缘两侧回波值较低。在使用中函数模板的长度、宽度、得分函数阈值均可调,但为适应业务化应用,阈值在做本地化调整后尽量保持不变。江苏沿江地区的阵风锋函数模板各阈值即如图 2所示,所有阵风锋个例的检验均使用该模板。
|
图 2 低仰角阵风锋细线函数模板 (a)回波模板, (b)回波得分函数 Fig. 2 Functional template for feature detector of the low elevation GF thin line (a) template, (b) scoring functions |
如前所述,CINAD/SA型号天雷达探测弱回波能力较强,0.5°仰角阵风锋特征明显时,当该阵风锋移近雷达站时,1.5°、2.4°相应位置也能探测到细线特征,甚至由于抬高仰角后,杂波干扰大幅度减少,细线特征更为明显。当高低空均存在回波时,原算法中空间差分反射率做法反而会削弱细线特征,因此本文算法采用多仰角反射率细线函数模板代替空间差分反射率细线函数模板。函数模板设计如图 3所示,与低仰角细线特征类似,不同的是模板较窄,为7个像素(图 3a),中心得分函数也略有不同,当中心值处于5~15 dBz时,给予高得分值(图 3b)。
|
图 3 高仰角阵风锋细线函数模板 (a)回波模板, (b)回波得分函数 Fig. 3 Functional template for feature detector of high elevation GF thin line (a) template, (b) scoring functions |
为降低识别算法的虚警率,本文根据阵风锋窄带回波的形状特征和数据分布特征,在算法中增加了回波带平坦度测试算法和角度判断两种方式来达到降低虚警的目的。
1.5.1 窄带回波平坦度计算由于0.5°反射率图像上,非阵风锋的窄带回波干扰较多,大部分识别算法虚警率均较高。为区别阵风锋窄带回波和其他窄带回波,程浩等(2011)采用了熵匹配的函式模板方法来计算雷达反射率因子图像上固定网格内的熵值,根据熵值大小来区分阵风锋回波和其他回波。此方法与边界取向无关,无需旋转模板来迎合阵风锋边界的不同取向,对于业务需求来说明显减少计算量。但是多变的阵风锋反射率数据分布限制了该方法的使用,该文献中所用数值均不能等于0,而实际情况却并非如此。本文借鉴了熵函式模板的思想,根据反射率因子图像色标设置标准,设计了简化的归一化回波带平坦度计算方法。
程浩等(2011)和阵风锋特征统计都表明阵风锋线段上数据的分布具有某种平坦度。平坦度可这样理解:在一定数值范围内(连续色标等级内),各色标等级内的数值个数分布较为平均。根据这一特性,回波带平坦度公式设计如下:
| $E = \sum\limits_{i = 1}^M {\frac{i}{M}} \frac{{{n_i}}}{N}$ | (1) |
式中,E为回波带平坦度大小,数值越低,回波带越平坦,说明回波带数值几乎一致;数值越高,回波带数值跨度越大、分布越杂乱。阵风锋回波带应较为平坦。N是网格内所有有效像素数目;ni为色标等级i内的像素数目;i为色标等级, M是色标分等级的总数。根据统计确定最高等级数4级,为0~25 dBz,如图 5中反射率因子色标前4等级所示。
|
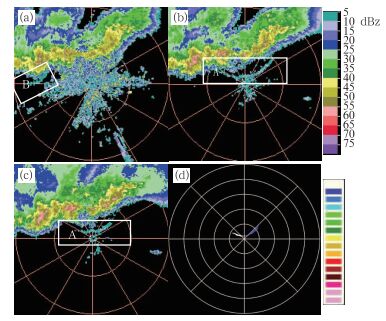
图 5 2009年6月14日17:48南京雷达阵风锋识别图 (a)0.5°反射率图像,(b)1.5°反射率图像,(c)2.4°反射率图像,(d)识别结果 Fig. 5 The gust front echo at 17:48 BT 14 June 2009 in Nanjing (a) 0.5°ZPPI image, (b) 1.5°ZPPI image, (c) 2.4°ZPPI image, (d) identification results |
由于阵风锋弱和数值多变的特性,若与程浩等(2011)类似把平坦度作为阵风锋主要特征进行线段筛选的话,会产生较高的虚警率。但若作为阵风锋回波带的约束条件之一,在计算综合得分值并提取的基础上再进行平坦度测试,可以有效剔除非阵风锋线段,从而降低虚警率。
1.5.2 弧度的判断从统计来看每一条阵风锋都是具有弧度的,因此在完成识别线段、提取疑似阵风锋线段后,可以通过判断每条“阵风锋”上若干线段的角度是否有变化来判断该阵风锋是否具有弧度:遍历属于该阵风锋的所有线段,当低于2段线段的角度不一样时,则判定该线条不是阵风锋。实践证明,加入弧度判断,几乎可剔除掉所有直线线段,从而降低虚警率。
1.6 动态权重函数的设计0.5°、1.5°、2.4°、时间差分反射率(由前后时次0.5°反射率数据相减得出)共四组反射率数值场在经过各自函数模板匹配后,得到四组0~1之间的得分数组,如何将这四组数组进行合成,突显阵风锋线段是成功识别的关键。在原算法中采用平均权重的做法,然而因各仰角阵风锋特征出现与阵风锋距离测站远近有直接关系:阵风锋离测站较远时,较高仰角无法探测到阵风锋窄带回波特征;距离测站较近时,低仰角阵风锋窄带回波与地物回波等混合而无法显示,每组得分值随着距离远近在综合得分中有着不一致的贡献。因此为能表征各组阵风锋特征得分值在不同距离的贡献,本文设计了一种与距离有关的动态权重函数来合成四组得分数组。具体做法如下:
| $\begin{array}{l} S = {s_0}\frac{{1 - {w_1} - {w_2}}}{3} + {s_d}\frac{{2\left( {1 - {w_1} - {w_2}} \right)}}{3} + \\ \quad \quad {s_1}{w_1} + {s_2}{w_2} \end{array}$ | (2) |
| ${w_1}\left\{ {\begin{array}{*{20}{l}} 0&{\quad {\kern 1pt} \quad r > 90}\\ {0.1\frac{{90 - r}}{{90}}}&{50 < r \le 90}\\ {0.35 + 0.1\frac{{50 - r}}{{50}}}&{0 < r \le 50} \end{array}} \right.$ | (3) |
| ${w_2}\left\{ {\begin{array}{*{20}{l}} 0&{\quad \quad r > 60}\\ {0.1\frac{{60 - r}}{{60}}}&{30 < r \le 60}\\ {0.35 + 0.1\frac{{30 - r}}{{30}}}&{0 < r \le 30} \end{array}} \right.$ | (4) |
式中,S为总得分值,s0为0.5°反射率函数模板匹配后的得分值,sd为时间差分反射率函数模板匹配后的得分值,s1为1.5°反射率函数模板匹配后的得分值,s2为2.4°反射率函数模板匹配后的得分值,w1为1.5°反射率得分值权重函数,w2为2.4°反射率得分值权重函数,r为阵风锋与测站的距离。
由式(2) 可见,总得分值由四部分组成,每一部分均被动态分配了权重值。当距离较远时,w1和w2均为0,得分值只由0.5°反射率得分值和时间差分反射率得分值组成,由于时间差分反射率阵风锋特征值更为明显,给其分配了较高的权重比重。当阵风锋离测站越近时,高仰角反射率得分值贡献越大,进入30 km范围内时,两者最高占比重达0.9。对应的低仰角反射率得分值由于在近测站区域阵风锋与地物回波等易混在一起,阵风锋特征易被掩盖,因此给0.5°和时间差分反射率两组得分值较低的权重,近距离阵风锋的识别更依赖高仰角反射率数据中阵风锋细线特征的正确识别。
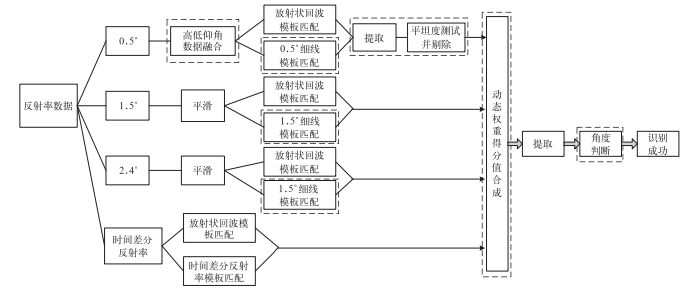
1.7 改进后的算法流程图经过上述数据预处理、多种阵风锋细线回波函数模板的改进与设计、采用动态权重函数的方式综合多种得分数组后,考虑阵风锋弧度和反射率数据分布的特征降低虚警率的措施后,改进的MIGFA算法流程图如图 4所示。流程图虚框部分为增加(改进)的算法模块。与原算法不同的是只采用了反射率数据作为算法基础数据,采用高仰角反射率数据替代了空间差分反射率数据。对多仰角反射率数据做相应预处理后,进行改进的函数模板匹配。低仰角数据匹配后的得分结果先进行第一次线状数据提取,对提取成功的线状数据做平坦度测试,剔除不满足平坦度阈值的线段;通过动态权重函数来组合0.5°、1.5°、2.4°、时间差分反射率四组得分值。对线段进行提取后再进行角度判断,最终得到被认为识别成功的阵风锋线段。
|
图 4 改进的MIGFA算法流程图 Fig. 4 Flow chart of the improving MIGFA |
利用江苏南京CINRAD/SA天气雷达探测到的2009年6月14日阵风锋个例对本文改进的MIGFA识别算法进行效果识别。2009年6月14日,东北冷涡带来的冷空气和低层切变线共同影响,并配合地面辐合线,给江苏中西部地区自北向南带来了一次大范围的雷雨大风和冰雹等强对流天气。南京天气雷达也捕捉到了此次强天气的回波特征,在多个仰角的反射率图像上多次出现了阵风锋窄带回波特征。
2.1 阵风锋回波特征及地面要素变化实况2009年6月14日17:18(北京时,下同),在南京天气雷达探测范围内初次探测到弱阵风锋窄带回波,至20:00左右所有阵风锋窄带回波特征彻底消失。其间共探测到三条阵风锋,最长一条过雷达站上空,且持续时间最长,约3 h; 另两条弧长较短,强度较弱,均约持续了1 h。窄带回波带最大反射率在13 dBz左右,最小值为5 dBz左右。阵风锋回波带过境时地面气象站要素出现了明显的变化,以南京溧水站为例,阵风锋过境时,气压上升(1003.5 hPa升至1006.7 hPa),温度下降(29.5℃降至24.5℃), 风速陡增(0.5 m·s-1增至11.3 m·s-1),方向突变(282°转至358°)。为典型的阵风锋过境时气象要素变化特征:气温骤降、气压上升、风速突增。
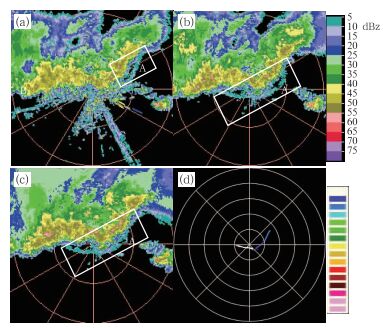
2.2 识别效果分析此次飑线过程过境途中,南京雷达共探测到该飑线系统中不同对流单体产生的三条阵风锋,根据出现先后分别用A、B、C表示(图 5~图 7相应白框内)。其中阵风锋A持续时间最长并经过南京雷达站上空,过境时该条阵风锋由于距离测站较近,在0.5°仰角反射率图像上只看到该阵风锋部分细线特征,其余部分与地面杂波等非降水回波混杂在一起,无法辨别,而在1.5°和2.4°仰角反射率图像上则捕捉到清晰的细线特征;弱阵风锋B在飑线移近雷达站的1 h内生成消亡(图 5a),未造成明显风灾;在飑线过境后对流回波带变形分裂,雷达站探测到东部一强回波块产生的阵风锋C(图 7a),随着该强对流回波块向东南方向移动远离测站,该阵风锋细线特征也消失在雷达图像中。为比较本文改进的MIGFA算法识别阵风锋A、B、C的能力,分别给出3条阵风锋均出现的三个时次的识别效果。
17:48(图 5),飑线即将过境时,飑线西部的强回波单体产生弱阵风锋B,由于该阵风锋特征较弱,算法未能成功识别;阵风锋A在0.5°反射率图像上无法辨别,而1.5°和2.4°图像上则呈现出清晰的细线特征,结合了0.5°、1.5°、2.4°三层数据的动态权重函数的综合得分技术充分体现了优势,成功识别出了该条阵风锋,如图 5d所示,不同色标表示算法识别出的不同阵风锋,该条阵风锋被算法认为由两条阵风锋线段组成(白色线段与深蓝色线段)。这是由于阵风锋中段与非降水回波混合(图 5b),算法无法识别此小段的线状特征,因此出现了断裂情况。总体来看识别出的阵风锋线段与观测特征基本吻合。
半小时后(18:12),如图 6所示,飑线前沿过雷达测站,0.5°反射率图像上,阵风锋B消失,阵风锋A在飑线右前侧呈现出部分细线特征,1.5°和2.4°图像上阵风锋A细线特征完整且明显。算法识别出了完整的阵风锋A细线特征。阵风锋识别细线由三条线段组成(图 6d),分析可知,白色和深蓝色线段由较高仰角的特征识别而出,浅蓝色线段则由0.5°图像的特征识别而出。通过动态权重函数合成得分值后展现了完整的阵风锋A。
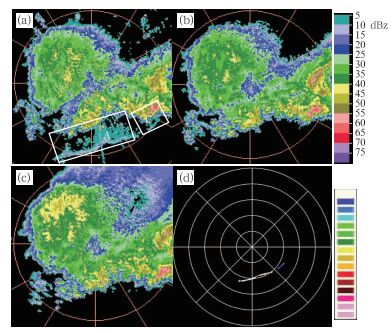
约1 h后(19:24),如图 7所示,飑线整体已移出雷达测站,对流回波带变形分裂,0.5°反射率图像上,阵风锋A弧度变小,几乎成一条直线;雷达探测到飑线系统右前侧一强回波块产生了阵风锋C。由于阵风锋离测站较远,1.5°和2.4°仰角的图像上已看不到阵风锋细线特征。算法成功识别出了阵风锋A和阵风锋C,均由0.5°阵风锋特征值贡献。
综合而言,改进后的MIGFA算法对此次阵风锋个例识别较为成功,通过动态权重函数组合多层得分值的方法保证了过测站阵风锋的完整性。另外从图像也可看出尽管低仰角图像近距离杂波干扰较多,较远距离也出现了放射状回波,但无虚假窄带回波被识别出。总体来看,改进后的MIGFA算法在识别阵风锋完整性、降低虚警率等方面均有较大改善。但由于采用同一函数模板捕捉线状特征,当初始阵风锋较弱时,算法无法识别。
3 识别效果评估对南京天气雷达2009—2012年探测到的较为典型的阵风锋窄带回波进行识别效果检验,共有120个阵风锋雷达回波样本进入检验评估,另有8个无阵风锋窄带回波样本也进入识别效果检验。这些阵风锋过境时在地面要素场上均出现了典型的要素特征值跳变。需要指出的是在评估工作中只要有属于阵风锋的线段被识别出,则认为对该阵风锋识别正确。因为只要有属于阵风锋的线段被识别出,则该条阵风锋就不会丢失。在后续研究工作中,将实现阵风锋跟踪算法,跟踪线段并判断断裂线段是否属于同一条阵风锋,最终给出需要防范风灾的区域范围,而不仅仅是线段。因此部分阵风锋线段的漏判不影响结果,本文认为识别正确,识别算法有效。
为体现本文算法改进效果,采取多种识别方案进行识别效果测试,利用成功率(POD)、虚假警报率(FAR)和临界成功指数(CSI)对每种方案进行识别效果评估。如式(5)~(7) 所示,其中ns为正确识别阵风锋数,nm为未能被识别的阵风锋数,nf为非阵风锋回波被算法误识别为阵风锋数。
| ${P_{{\rm{OD}}}} = \frac{{{n_{\rm{s}}}}}{{{n_{\rm{s}}} + {n_{\rm{m}}}}}$ | (5) |
| ${F_{{\rm{AR}}}} = \frac{{{n_{\rm{f}}}}}{{{n_{\rm{s}}} + {n_{\rm{f}}}}}$ | (6) |
| ${C_{{\rm{SI}}}} = \frac{{{n_{\rm{s}}}}}{{{n_{\rm{s}}} + {n_{\rm{m}}} + {n_{\rm{f}}}}}$ | (7) |
所有识别方案均基于MIGFA算法的基本原理:使用一种或多种函数模板。选用方案如下:
方案一:采用李劲等(2011)的方案,利用江淮阵风锋特征统计结果设计的0.5°细线回波函数模板,只利用0.5°函数模板进行匹配识别。
方案二:采用本文1.4.1根据江苏沿江阵风锋特征统计结果设计的0.5°细线回波函数模板,按照MIGFA原算法,结合时间差分反射率细线回波函数模板、空间差分反射率细线回波函数模板等进行平均权重的组合得分进行识别。
方案三:采用本文1.4.2设计的高仰角阵风锋线状函数模板,引入1.5°、2.4°反射率函数模板取代空间差分反射率函数模板,并利用1.6设计的动态权重函数组合多组得分数组进行识别。
方案四:采用方案三并结合本文1.5设计的降低虚警率的做法进行识别。
识别效果评估如表 1所示。
|
|
表 1 四种方案阵风锋识别效果检验 Table 1 Result verification of the four GF identification schemes |
由表 1可见,方案一的成功率最低,方案三和方案四的成功率最高达0.68。增加降低虚警率做法后虚假警报率由0.3下降至0.16,临界成功指数由0.53提高至0.60。多种方案识别结果对比说明,基于本地雷达数据和阵风锋特征统计结果改进的MIGFA算法识别效果最好。考虑了阵风锋细线、移动、阵风锋高度与距离关系等特征,综合0.5°、1.5°、2.4°反射率数据及时间差分反射率数据,调整、改进算法中的阈值、函数模板,设计动态权重方案提高综合有效得分值的做法,有效提高了识别成功率;利用阵风锋弧度和强度分布的特点,通过角度判断和反射率平坦度测试进一步降低了虚警率,达到了提高识别成功率的目的。
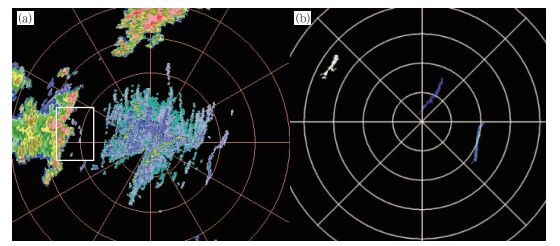
但是从表 1数据也可看出,方案四仍存在漏报和虚假警报,分析识别失败原因:由于算法中多种函数模板阈值相对固定,当存在与制定的阵风锋细线函数模板特征相一致的回波带时,误判就会出现。图 8a为阵风锋弱回波特征刚被探测到时,由于距离雷达站较远,且阵风锋回波带有多处断裂(图 8a白框所示),识别算法尽管识别出了三条线状回波带,但均非阵风锋,白色为对流云后侧的非降水弱回波带,两条蓝色线段为测站附近的非降水回波带。若能结合对流回波的落区和移动方向,可剔除两条蓝色线段,排除对流回波块附近的弱回波带仍存在较大困难。
|
图 8 阵风锋识别图 (a)0.5°反射率图像, (b)识别结果 Fig. 8 Identification of the gust front in radar image (a)0.5°ZPPI image, (b) the identification results |
本文根据CINRAD/SA天气雷达探测到的江苏沿江地区阵风锋回波特征,对MIGFA阵风锋识别算法进行了改进:一是考虑平滑算法的使用和低仰角数据融合;二是根据阵风锋回波统计特征改进了0.5°反射率回波细线函数模板,并设计了较高仰角(1.5°/2.4°)反射率回波细线函数模板,引入1.5°和2.4°双层反射率细线函数模板替代原空间差分反射率函数模板。三是考虑到阵风锋特征与阵风锋距离测站距离的关系,设计了动态权重函数组合多组得分值。并通过弧度判断和阵风锋回波平坦度测试的方式,进一步降低虚警率。最后采用个例识别效果分析和检验评估算法检验了改进的识别算法。得出以下结论:
(1) 平滑算法的有限使用和低仰角数据的融合,尽可能地保存和凸显了每个仰角的阵风锋回波特征。
(2) 根据本地阵风锋的统计特征结果,综合0.5°、1.5°、2.4°及时间差分反射率数据,调整、改进MIGFA算法中的阈值、低仰角阵风锋细线函数模板,设计较高仰角阵风锋细线函数模板,通过设计动态权重方案提高阵风锋数据的有效得分值。改进后的MIGFA算法将临界成功指数从0.39提高至0.60,识别效果良好。
(3) 引入弧度判断和反射率平坦性测试的做法使得虚假警报率从0.34降至0.16。
由于阵风锋回波弱这个主要特点,要继续提高成功识别率并降低虚警率仍是非常困难的命题。下一阶段我们将结合地面天气实况、雷暴母体与其触发的阵风锋关系等进行更详细的分析,以期从阵风锋形成的机理角度分析,进一步提高识别率。若该算法向其他速度数据质量较好的天气雷达进行推广时,仍将保留原MIGFA算法中关于径向速度数据特征识别和应用部分。最终增加跟踪算法,以期达到阵风锋的监测预警目的,实现业务化应用。
致谢:本工作得到中国气象科学研究院胡志群博士的大力帮助,在此表示感谢。
陈钢.阵风锋的检测与识别. 2009.西安:西安电子科技大学. http://cdmd.cnki.com.cn/Article/CDMD-10701-1011077226.htm
|
程浩, 刘国庆, 2011. 基于熵函式模板的阵风锋自动识别与实现[J]. 计算机工程与设计, 32(6): 2173-2175. |
何红红, 慕熙昱, 赵宏玲, 等, 2013. 阵风锋自动识别算法的试验研究[J]. 气象科学, 33(5): 519-525. DOI:10.3969/2012jms.0132 |
李柏, 古庆同, 李瑞义, 等, 2013. 新一代天气雷达灾害性天气监测能力分析及未来发展[J]. 气象, 39(3): 265-280. DOI:10.7519/j.issn.1000-0526.2013.03.001 |
李劲, 徐芬, 顾松山, 2011. 基于雷达反射率的阵风锋自动识别算法研究[J]. 第28届中国气象学会年会. |
王婷婷, 王迎春, 陈明轩, 等, 2011. 北京地区干湿雷暴形成机制的对比分析[J]. 气象, 37(2): 142-155. DOI:10.7519/j.issn.1000-0526.2011.02.003 |
吴芳芳, 王慧, 韦莹莹, 等, 2009. 一次强雷暴阵风锋和下击暴流的多普勒雷达特征[J]. 气象, 35(1): 55-69. DOI:10.7519/j.issn.1000-0526.2009.01.007 |
席宝珠, 俞小鼎, 孙力, 等, 2015. 我国阵风锋类型与产生机制分析及其主观识别方法[J]. 气象, 41(2): 133-142. DOI:10.3969/2014jms.0039 |
夏文梅, 徐芬, 谢志清, 等, 2011. 基于VAD技术的迭代法在实测多普勒速度缺测区域的填补研究[J]. 气象学报, 69(1): 161-169. DOI:10.11676/qxxb2011.014 |
徐芬, 夏文梅, 吴蕾, 等, 2007. 多普勒天气雷达PPI图散度分布信息提取[J]. 气象, 33(11): 21-27. DOI:10.7519/j.issn.1000-0526.2007.11.004 |
俞小鼎, 2012. 2012年7月21日北京特大暴雨成因分析[J]. 气象, 38(11): 1313-1329. |
袁子鹏, 王瀛, 催胜权, 等, 2011. 一次中纬度飑线的阵风锋发展特征分析[J]. 气象, 37(7): 814-820. DOI:10.7519/j.issn.1000-0526.2011.07.005 |
张涛, 李柏, 杨洪平, 等, 2013. 三次雷暴导致的阵风锋过程分析[J]. 气象, 39(10): 1275-1283. DOI:10.7519/j.issn.1000-0526.2013.10.005 |
郑佳锋, 张杰, 朱克云, 等, 2013. 阵风锋自动识别与预警[J]. 应用气象学报, 24(1): 117-125. DOI:10.11898/1001-7313.20130112 |
Bedard Jr, Hooke W H, Beran D W, 1977. The dulles airport pressure jump detector array for gust front detection[J]. Bull Amer Meteor Soc, 58: 920-926. DOI:10.1175/1520-0477(1977)058<0920:TDAPJD>2.0.CO;2 |
Crook N A, Sun Juanzhen, 2004. Analysis and forecasting of the low-level wind during the Sydney 2000 forecast demonstration project[J]. Wea Foresting, 2(19): 151-167. |
Delanoy R L, Troxel S W, 1993. Machine Intelligent Gust Front Detection[J]. The Lincoln Lab J, 6(1): 187-212. |
Hermes L G, Wrrt A, Smith S D, et al, 1993. The gust-front detection and wind-shift algorithms for the terminal Doppler weather radar sysem[J]. J Atmos Oce Tech, 10: 693-709. DOI:10.1175/1520-0426(1993)010<0693:TGFDAW>2.0.CO;2 |
Smally D J, Bennett B J, Frankel R, 2005. MIGFA:The Machine Intelligent Gust Front Algorithm for NEXRAD[J]. 32nd Conference on Radar Meteorology. |
Troxel S, Frankel B, Echels B, et al, 2002. An Improved gust front detection capability for the ASR-9 WSP[J]. 10th Conference on Aviation. |
Uyeda H, Zrnic D S, 1986. Automatic detection of gust fronts[J]. J Atmos Oceanic Technol, 3: 36-50. DOI:10.1175/1520-0426(1986)003<0036:ADOGF>2.0.CO;2 |
 2016, Vol. 42
2016, Vol. 42