2. 南京信息工程大学 大气科学学院,南京 210044;
3. 气象灾害教育部重点实验室(南京信息工程大学),南京 210044;
4. 浙江省气象服务中心,杭州 050081;
5. 中国气象局数值预报中心,北京 100081;
6. 解放军理工大学气象海洋学院,南京 050081;
7. 中国卫星海上测控部,江阴 21443
2. College of Atmospheric Science, Nanjing University of Information Science and Technology, Nanjing 210044;
3. Key Laboratory of Meteorological Disaster (NUIST), Ministry of Education, Nanjing 210044;
4. Center of Meteorological Service of Zhejiang, Hangzhou 310017;
5. Numerical Weather Prediction Centre of CMA, Beijing 100081;
6. Institute of Meteorology and Oceanography, PLA University of Science and Technology, Nanjing 211101;
7. China Satellite Maritime Tracking and Control Department, Jiangyin 310017
由于初值误差、模式误差及大气的混沌特性,传统的单一数值预报存在不确定性问题,Leith(1974)提出的集合预报思想为解决数值预报不确定性问题提供了一个有效手段。目前集合预报已广泛应用于数值预报的各个领域,各国气象中心也更多地采用集合预报方法来提高数值预报技巧(Toth et al,1997;Molteni et al,1996),尤其是对暴雨,台风等灾害性强天气,集合预报的作用显得尤为突出(陈静等,2005;谭燕等,2010;张涵斌等,2014)。
为了融合不同模式的预报不确定信息,提高预报技巧,Krishnamurti等(2000b; 2007)提出了超级集合预报思想。该思想将时间序列分为两段,一段为训练期,一段为预报期,通过建立训练期不同模式预报与实况的回归方程来收集各模式的预报技巧信息,并根据这些信息将预报期内多模式预报进行集成。Krishnamuriti等(2000a)将该方法用于气候预测和天气数值模拟试验,表明超级集合预报技巧优于单个模式预报,并且比简单的集合平均预报结果更为准确。此后,一系列的研究均对超级集合预报以及多模式集成方法的效果进行了验证(智协飞等,2014)。Hagedorn等(2005)使用DEMETER资料,进行单一模式预报和多模式集成预报的对比试验,从基本概念的角度阐述了多模式集成方法优于单模式预报的原因。Krishnamurti等(2003)采用超级集合预报方法对500 hPa高度场进行分析,结果显示超级集合预报对于位势高度方差较大的地区预报有明显提高,并提高了距平相关系数技巧;智协飞等(2009)基于TIGGE资料对北半球中纬度地区地面气温进行超级集合预报试验,并引入了滑动训练期方法提高了预报技巧;林春泽等(2009)基于TIGGE资料,采用超级集合、多模式集合平均和消除偏差集合平均对四个中心地面气温预报进行集成,结果表明超级集合和消除偏差集合平均有效降低了预报误差,预报效果优于最好的单中心预报和多模式集合平均。对于降水预报,多模式集成方法也显示出一定的优势。Krishnamurti等(2000b;2007)利用多分析-多模式超级集合预报系统进行了降水预报试验,表明超级集合预报预报技巧明显高于单一模式。
热带气旋路径及强度预报,一直是近年来的一个研究热点,从20世纪90年代开始热带气旋路径预报效果得到了较大提高。而将多模式集成方法应用于热带气旋预报,也是提高预报技巧的一个极为有效的途径,Krishnamurti等(1999)指出超级集合预报对飓风的预报技巧要优于单模式预报。Goerss (2000)指出通过对多个模式预报结果进行集成,可以得到更为准确的热带气旋路径预报。Williford等(2003)对1999年大西洋飓风进行了预报试验,表明在1~5 d预报时效内,多模式超级集合预报对飓风路径和强度预报的误差小于单一模式预报。Vijaya Kumar等(2003)等采用多中心业务预报资料对太平洋地区热带气旋路径和强度进行超级集合预报试验,表明超级集合预报结果优于单一模式预报以及集合平均。
西太平洋地区为热带气旋多发区,我国地处太平洋西岸,特殊的地理位置使得我国频繁遭受热带气旋袭击,常常造成严重的人民生命财产损失,并给国家经济建设和社会稳定运行带来巨大影响,因此开展西太平洋地区热带气旋路径和强度多模式集成预报方法的研究具有较大意义。周文友等(2012)采用TIGGE资料对2009年西太平洋热带气旋进行24、48和72 h时效的多模式集成预报,表明多模式集成预报的表现始终优于最好的单模式预报及集合平均。为了进一步深化对多模式集成方法的认识,本文在前人工作的基础上,采用连续3年的TIGGE资料对西太平洋地区热带气旋路径和强度进行多模式集成预报,并将预报时效延长至120 h,以了解多模式集成方法在更长预报时效的有效性;同时,引入四种多模式集成方法进行对比,包括集合平均、加权集合平均、消除偏差集合平均以及加权消除偏差集合平均(超级集合)。通过分析不同的集成方案的特点,可以更加深入地认识多模式集成方案成功的原因,尤其是加权集成过程和消除偏差集成过程对多模式集成方案的作用。
1 资料与方法 1.1 资料选取TIGGE(THORPEX全球交互式大集合)是THORPEX项目的主要组成部分,该全球性的研究项目旨在提高1天至2周内的强天气预报。TIGGE数据集包含全球10个数值预报中心的集合预报数据,从2006年10月开始归档。TIGGE数据集为一系列科学研究(包括集合预报、大气可预报性以及强天气预报的研究)提供了一个重要的数据来源(Zhi et al,2012;刘永和等,2013)。第六届WMO热带气旋国际研讨会提出将所有的热带气旋相关的数值预报产品,包括集合预报产品对业务及研究用户开放,发放的数据包括各种强天气预报及热带气旋预报。TIGGE资料的发放为科学研究提供了便利,本文即采用TIGGE数据集中CMA、ECMWF、JMA以及NCEP四个中心2010、2011及2012年连续3年的集合平均预报资料,对西太平洋地区台风路径及中心气压进行多模式集成试验,预报时效为24、48、72、96和120 h。实测资料采用美国联合台风预警中心(Joint Typhoon Warning Center,JTWC)最佳路径数据集。
本文多模式集成试验的对象是2010、2011及2012年58个热带气旋的路径和强度预报,其中1013号台风鲇鱼(Megi)为超强台风,生命史长达11 d,其峰值的中心附近最大风力达72 m·s-1,中心最低气压为895 hPa,其以西偏南路径移入南海后,突然北翘,这一突变给业务预报带来了很大挑战(许映龙,2011),为本文的重点研究个例。
1.2 方法简介 1.2.1 多模式集合平均将多个集合预报结果通过求平均可以转化为一个预报结果,即集合平均。集合平均也是集合预报的最初级产品。对于多模式集成预报而言,最简单的集成方法就是多模式集合平均(ensemble mean,简称EMN),计算公式如下
| $ {\mathit{F}_{\mathit{EMN}}} = {\rm{ }}\frac{1}{\mathit{N}}\sum\limits_{\mathit{i} = 1}^\mathit{N} {{\mathit{F}_i}} $ | (1) |
式中,FEMN为集合平均,N为参与集成的模式总数,Fi为某一中心单一模式的集合平均预报。
1.2.2 加权集合平均鉴于不同中心的单模式预报能力有所不同(尤凤春等,2009;张国华等,2011),如果仅采用简单平均,即各单模式预报等权重的话,集合结果中并未体现各模式预报能力的差异,因此在集成过程中,可以通过将不同模式赋予不同的权重,得到一个不等权的集合平均。为了单独了解权重系数在多模式集成过程中的作用,本文在集合平均的基础上引入一种加权集合平均方法。该方法首先将时间序列分为两个时期:训练期和预报期,从训练期中各模式的表现得到统计信息,进而得到各模式权重系数,用于预报期的多模式集成预报,这种采用加权的方法,我们称为加权集合平均法(weighted ensemble mean,WEMN),计算公式如下:
| $ {\mathit{F}_{\mathit{WEMN}}} = {\rm{ }}\sum\limits_{\mathit{i} = 1}^\mathit{N} {{\mathit{a}_\mathit{i}}{\mathit{F}_i}} $ | (2) |
式中,FWEMN为加权集合平均,ai为各模式在训练期得到的权重,Fi为各模式在预报期的预报,N为参与集成的模式个数。
权重系数ai的确定参照周文友(2012)的方法,即首先得到训练期各模式的预报误差(这里采用平均绝对误差),取其倒数,某一模式预报误差倒数在所有模式成员误差倒数之和中占的比重,作为权重系数ai,即
| $ {\mathit{a}_\mathit{i}} = \left({1/{\mathit{E}_\mathit{i}}} \right)\sum\limits_{\mathit{i = 1}}^\mathit{N} {\left({1/{\mathit{E}_\mathit{i}}} \right)} $ | (3) |
式中Ei为各个模式预报误差,由训练期样本的平均绝对误差所得,如下式:
| $ {\mathit{E}_\mathit{i}} = \frac{1}{\mathit{M}}\sum\limits_{j = 1}^M {|{\mathit{F}_{\mathit{ij}}} - {\mathit{O}_\mathit{j}}|} $ | (4) |
式中,M为训练期样本数目,j表示训练期样本序列号,Fij为第i个模式预报第j个样本的预报值,Oj为第j个样本的观测值。
1.2.3 消除偏差集合平均Krishnamurti(1999)指出模式往往存在固有的系统性偏差,可以根据训练期的模式表现得到该模式的偏差信息,并在预报期予以消除。通过消除偏差可以得到无偏的集合平均(bias removed ensemble mean,BREM),如下式:
| $ {\mathit{F}_{\mathit{BREM}}} = \mathit{\bar O + }\frac{1}{\mathit{N}}\sum\limits_{i = 1}^N {\left({{\mathit{F}_\mathit{i}} - {{\mathit{\bar F}}_\mathit{i}}} \right)} $ | (5) |
式中,FBREM为消除偏差集合平均预报,O为训练期观测值的平均,Fi为训练期各模式预报值的平均,Fi为预报期各模式的预报。此种方法与集合平均的差异仅在于参与集成的模式预报是无偏的,因此该方法可以体现出消除偏差过程在多模式集成中的作用。
1.2.4 加权消除偏差集合平均综合考虑了不同模式的权重和模式偏差,首先由训练期得到各模式的权重系数,同时得到训练期内,模式预报相对于观测的偏差,同时采用加权及消除偏差方法,得到加权消除偏差集合平均,即超级集合预报(superensemble,SUP)
| $ {\mathit{F}_{\mathit{SUP}}} = \mathit{\bar O + }\sum\limits_{i = 1}^N {{\mathit{a}_\mathit{i}}\left({{\mathit{F}_\mathit{i}} - {{\mathit{\bar F}}_\mathit{i}}} \right)} $ | (6) |
式中,FSUP代表超级集合预报,其余变量意义如上文。相对于集合平均而言,超级集合既对单模式预报进行了无偏化处理,又赋予各单模式预报不同的权重系数,因此理论上更为完善(董海平等,2013)。
2 试验方案设计采用集合平均(EMN)、加权集合平均(WEMN)、消除偏差集合平均(BREM)和超级集合(SUP)四种方案,基于2010、2011及2012年3年的CMA、ECMWF、JMA、NCEP四个TIGGE中心的热带气旋路径和中心气压集合平均预报资料,进行时效为24、48、72、96和120 h的集成预报。并采用平均绝对误差(Mean Absolute Error,简称MAE)和偏差(Bias,简称B)来进行预报结果检验。
平均绝对误差:
| $ \mathit{MAE} = \frac{1}{\mathit{M}}\sum\limits_{j = 1}^M {|{\mathit{F}_\mathit{j}} - {\mathit{O}_\mathit{j}}|} $ | (7) |
偏差:
| $ {\mathit{B}_\mathit{j}} = {\mathit{F}_\mathit{j}} - {\mathit{O}_\mathit{j}} $ | (8) |
式中,Fj为第j个样本的预报值,Oj为第j个样本的观测值,M为样本总数。
考虑到资料有限,且预报时效越长,资料越匮乏,本文的多模式集成试验设置为将每年所有台风个例中,前一半个例作为训练期样本:2010年有14个台风个例,则前7个作为训练期样本,后7个作为预报期样本;2011年有21个台风个例,则前11个作为训练期样本,后10个作为预报期样本;2012年有23个台风个例,则前12个作为训练期样本,后11个作为预报期样本。
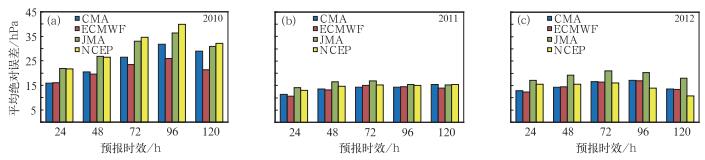
3 试验结果分析 3.1 各中心单模式预报评估首先对各中心预报能力进行评估。图 1给出了CMA、ECMWF、JMA及NCEP四个中心2010、2011和2012年每年所有个例样本路径预报的平均绝对误差,从图中可以看出不同的中心预报能力有所不同,2010和2011年,ECMWF具有较高的预报技巧,各个时效预报误差均处于较低水平,如2010年24、48和72 h的预报误差分别为82、155和219 km,低于其他三个中心,而CMA表现较差,如2010年24、48和72 h时效预报,CMA平均绝对误差为147, 256和365 km,明显高于其他三个中心,而误差比ECMWF高出65、100和145 km。2011及2012年预报情况也类似。另外,对于2012年,24 h预报时效误差较低的预报为ECMWF和NCEP,48~120 h预报时效最好的单模式预报为NCEP,误差甚至低于ECMWF,可能原因是2012年NCEP对其模式进行了升级和改进,因此提高了预报技巧。
|
图 1 CMA, ECMWF, JMA和NCEP四个中心对西太平洋地区热带气旋路径预报平均绝对误差 Fig. 1 Mean absolute error of Western Pacific tropical cyclone track forecasts for model forecasts of CMA, ECMWF, JMA and NCEP |
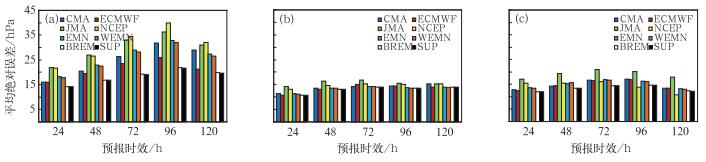
图 2与图 1类似,但为中心气压预报。首先可以看出2010年各单模式预报误差要大于2011和2012年,原因可能是2010年各单模式存在显著的强度预报偏弱的系统性偏差,而随着各中心对各自模式的改进和升级,使得2011和2012年误差有所减小。对于中心气压预报,2010年ECMWF同样表现出较小的预报误差,尤其是对于较长预报时效,ECMWF相对于其他中心的优势更为明显。如96 h ECMWF的误差为26 hPa,显著低于其他三个中心预报,而JMA和NCEP则表现出较大的预报误差,96 h预报时效的误差分别为36.7和40 hPa。对于2011和2012年,四个中心的表现相差不大,相对而言JMA预报误差略大。
图 3给出了CMA、ECMWF、JMA及NCEP四个中心对“鲇鱼”的路径预报以及JTWC最佳路径(OBS),预报时效分别为24、48、72、96和120 h,路径点的时间间隔为12 h。由于随着预报时效的延长,资料逐渐变少,因此不同预报时效对应的路径点数目不同,如对于24 h时效的预报,给出了起报时间间隔12 h(即由10月13日1200 UTC, 10月13日1212 UTC, …, 10月22日1200 UTC起报),预报24 h的路径点,共18个。对于48、72、96和120 h的预报时效,根据起报时次数目的不同分别得到了17、16、12以及12个预报的路径点。从图 3可以看出“鲇鱼”路径在17°N、118°E附近产生了明显的北翘,对于24 h预报,各个中心路径预报与实况较为接近,需要注意的是,各中心的前4~5个路径点均落在了实况的左侧,而后几个路径点又都偏向了实况的右侧。随着预报时效的延长,各个中心的路径预报呈现出很大的离散状态,而且各个中心预报在路径点北翘之后的离散程度更为明显,各中心对“鲇鱼”北翘之后的路径预报差异较大,同时也说明“鲇鱼”的北翘过程包含有较大的预报不确定性。

|
图 3 CMA, ECMWF, JMA和NCEP四个中心对“鲇鱼”路径预报以及JTWC最佳路径(OBS), 预报时效分别为(a) 24 h, (b) 48 h, (c) 72 h, (d) 96 h及(e) 120 h Fig. 3 Track forecasts of Typhoon Megi from CMA, ECMWF, JMA and NCEP and JTWC Best Track (OBS) (a) 24 h, (b) 48 h, (c) 72 h, (d) 96 h and (e) 120 h |
对于多模式集成而言,当增加参与集成的模式数目,会增加模式的不确定性信息,理论上有助于提高多模式集成的总体性能,然而某些预报环境下,某些模式可能表现较差,对集成预报技巧产生负面影响。对于这种较差模式,弃之不用是不合适的,因为在另外一些预报环境下,这些较差模式可能会有较高的预报技巧,为多模式集成预报做出贡献。
上文得知,CMA预报在2010、2011及2012年3年24~96 h预报时效的路径预报表现最差,前人研究表明,当多模式集成引入较差模式预报时,有可能对集成预报结果产生消极作用(Zhi et al,2012),但是对于等权重集合(EMN)和不等权重集合(WEMN)方法,这种较差模式的消极作用又会多大程度影响集成预报结果,值得深入研究。
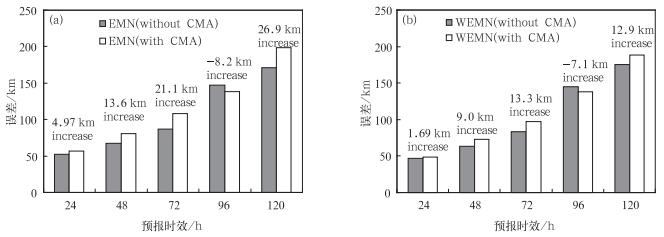
图 4给出了引入CMA之前(without CMA)和之后(with CMA)对台风个例“鲇鱼”路径预报平均绝对误差变化,集成方法采用EMN和WEMN。我们重点关注各个预报时效的‘with CMA’相对于‘without CMA’的误差变化。可以看出,当引入一个较差的集合成员CMA时,24、48、72和120 h预报时效路径预报误差不可避免的都有所增加,但对于EMN(图 4a),路径预报误差的增幅(即‘with CMA’和‘without CMA’之差)十分显著(24 h时效为4.97 km,48 h时效为13.6 km,72 h时效为21.1 km,120 h时效为26.9 km),而对于WEMN(图 4b),其路径预报误差虽然也有所增加(24 h时效1.69 km,48 h时效为9.0 km,72 h时效为13.3 km,120 h时效为12.9 km),但是增幅明显不及EMN方法中预报误差增加幅度。所以当引入一个明显较差的单模式预报时,加权集合平均能够在吸收此单模式预报信息的同时,最大程度减少该较差单模式预报对集成预报技巧的负面影响。
|
图 4 引入CMA模式预报之前(without CMA)和之后(with CMA)的“鲇鱼”路径预报误差, 同时给出了误差变化 (a) EMN, (b) WEMN Fig. 4 Track forecast error of Typhoon Megi before and after using CMA model (a) EMN and (b) WEMN |
参与贡献的模式越多,所能提供的不确定性信息越大,不同的模式,对于不同的预报环境,其表现各异,有好有坏,在进行多模式集成预报时,并不了解某个单模式会对集成预报结果产生积极或者消极贡献,因此根据其在训练期的表现来确定其相应的权重,使每个模式都能在预报期做出其应有的贡献,是更为合理的方法。
3.3 消除偏差集合平均相对于集合平均的优势对于数值模式预报而言,可能存在较为显著的系统性偏差,该系统性偏差普遍存在于模式训练期和预报期中(李柏平等,2012),因此通过训练期中某一模式预报样本和观测样本,可以了解该模式的偏差信息,在预报期多模式集成过程中予以消除。
图 5给出了24、48、72、96及120 h预报时效的台风“鲇鱼”路径点的中心气压预报偏差样本序列Bi,分别列出了各个中心单模式预报,以及EMN和BREM两种集成方法的预报结果,由于资料有限,对应的路径点个数分别为18、17、16、12及12个。从图可以看出,对于中心气压预报,各中心均产生了较大的正偏差,EMN方法并不能将该偏差消除,而BREM可以显著消除该系统性偏差。
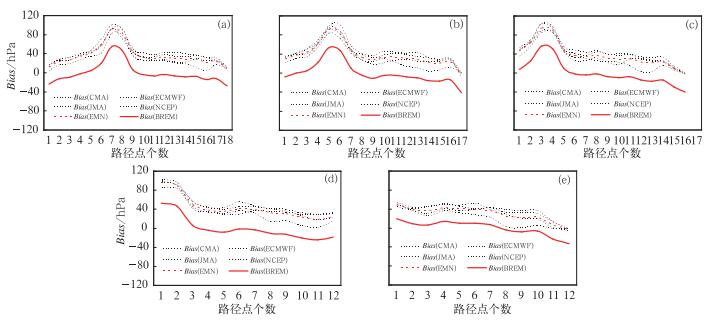
|
图 5 “鲇鱼”路径点预报偏差, 包括各中心预报及EMN、BREM方法 (a) 24 h, (b) 48 h, (c) 72 h, (d) 96 h, (e) 120 h Fig. 5 Central pressure forecast bias for track points of Typhoon Megi by EMN, BREM and four single models (a) 24 h, (b) 48 h, (c) 72 h, (d) 96 h and (e) 120 h |
上文给出了WEMN及BREM相对于EMN的优势,为了了解综合考虑了对参与集成的模式赋予不同权重及消除模式预报偏差的超级集合方法(SUP)相对于其他三种方法具有怎样的优势,以下对EMN、WEMN、BREM和SUP四种集成方法的效果进行较为全面的检验。
与图 3类似,图 6给出了24、48、72、96以及120 h预报时效的四种集成方法对“鲇鱼”的路径预报,同时给出了JTWC Best Track作为实况(OBS)。首先可以看出,随着预报时效的延长,各集成方法预报误差有所增加。对于24 h预报,四种方法的集成预报结果与实况较为接近,对于“鲇鱼”路径的北翘位置把握地也较准确,在其路径北翘之后,各集成预报略微偏右;而48和72 h时效预报,各集成方法的偏离程度有所增加,且对于北翘位置的预报也有所偏差;96 h预报,实况路径在15.3°N、118°E附近北翘,而各集成方法预报的北翘位置在15.3°N、115°E附近,说明在“鲇鱼”北翘之后,各集成方法对经度预报存在一定偏差;120 h时效的预报,各集成方法预报误差有了进一步增加,但相对于各中心单模式预报(图 3)有了明显的改善。
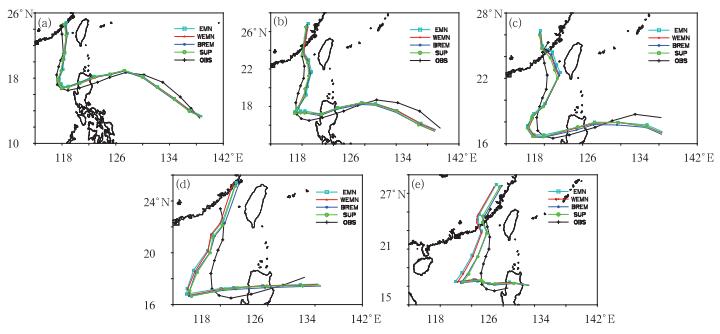
|
图 6 “鲇鱼”路径预报, 包括EMN, WEMN, BREM和SUP四种方法以及JTWC最佳路径(OBS) (a) 24 h, (b) 48 h, (c) 72 h, (d) 96 h, (e) 120 h Fig. 6 Track forecasts for Typhoon Megi, including forecasts from EMN, WEMN, BREM, SUP methods and the JTWC Best Track OBS (a) 24 h, (b) 48 h, (c) 72 h, (d) 96 h and (e) 120 h |
其次,我们发现不同的集成方法,各自表现也有所不同,对于时效较短的预报,四种方法效果相差不大,其中SUP方法对于“鲇鱼”北翘之后的路径预报略好。96 h时效的预报,SUP方法对于北翘位置的预报略微准确,当预报时效为120 h,SUP和BREM的表现明显好于另外两种方法,其中SUP方法对北翘点的预报比最差的EMN方法接近实况将近一个经度,而在北翘之后的路径也更接近实况。
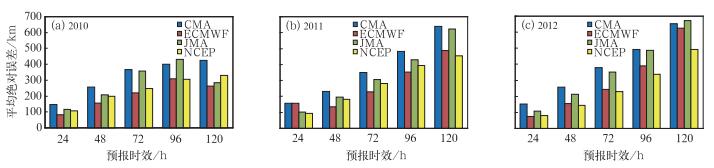
图 7给出了3年预报期内四个中心以及四种多模式集成方法的路径预报平均绝对误差,预报时效为24、48、72、96及120 h。由图中可以看出,四种集成方法相对于单模式预报均表现出了更高的预报技巧,这种优势体现在了24~120 h预报时效上,其中SUP方法较其他集成方法更为准确。如2012年(图 7c)120 h预报时效的结果,NCEP(最好的单模式预报)、EMN以及SUP的预报误差分别为491、539和430 km,表明SUP方案显著优于最好的单模式预报以及EMN,但也有例外情况,如2011年(图 7b)48和72 h预报结果,ECMWF预报误差小于四种多模式集成方法,这是由于在进行多模式集成过程中,ECMWF预报要显著优于其他三个参与集成的成员,因此集成预报结果有可能不及具有明显优势的ECMWF预报。
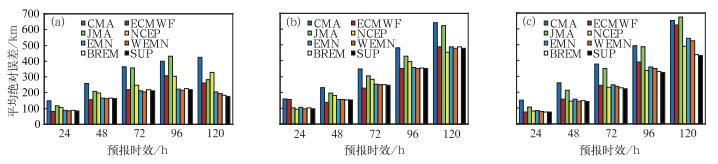
|
图 7 四个中心以及四种多模式集成方法对3年预报期内路径预报的平均绝对误差, 预报时效为24, 48, 72, 96及120 h (a) 2010年, (b) 2011年, (c) 2012年 Fig. 7 Mean absolute error of track for four single model forecasts and four multimodel ensemble forecasts (a) 2010, (b) 2011 and (c) 2012 |
图 8给出了中心气压预报结果,可以看出对于2010年(图 8a),BREM和SUP方案在各个预报时效均优于其他两种集成方法,可能的原因是该年各单模式存在显著的强度预报偏弱的系统性偏差,因此BREM和SUP方案优于其他两种集成方法。其余两年SUP方案也表现出较好的预报效果,其预报误差普遍低于各单模式预报以及其余三种多模式集成方法,其中对于2012年96和120 h预报,由于NCEP预报误差显著小于参与集成的其他三个单模式预报,因此其误差也小于四种集成预报结果。总体上看,由于综合考虑了去除偏差以及将参与集成的单模式预报赋予不同的权重,SUP方案能够得到最优的集成预报结果。
5 结论与讨论本文基于TIGGE资料中CMA、ECMWF、JMA以及NCEP四个中心连续3年的热带气旋路径和中心气压预报资料,采用集合平均、加权集合平均、消除偏差集合平均以及加权消除偏差集合平均(超级集合)四种集成方法进行预报时效为24、48、72、96及120 h的集成预报试验,并对单模式预报的预报效果进行对比,对不同集成方法的特点进行比较分析,综合评估了各种单模式预报和多种集成方案的预报效果,得出了如下结论:
(1) 对连续3年的热带气旋预报的统计发现,不同中心单模式预报能力有所不同,其中3年的CMA预报效果均较差,2010、2011年的ECMWF预报和2012年的NCEP预报效果最优。在120 h预报时效内,随着预报时效的延长,各中心的预报能力均有所下降,且各中心之间的离散度随预报时效的延长而增加。
(2) 加权集合平均方法可以对参与多模式集成的单模式预报赋予相应权重,保证不同的集成成员均参与贡献的同时,降低较差成员对集成预报技巧的影响,表明加权过程是多模式集成方法中的有效手段。
(3) 消除偏差方法可以从训练期得到偏差信息,并在多模式集成过程对偏差进行消除。当参与集成的单模式预报存在显著系统性偏差时,该方法能够显著提高预报准确性,表明在多模式集成过程中,消除偏差过程极为重要。
(4) 总体上,四种多模式集成方案在24~120 h预报时效内要优于单模式预报,由于综合考虑了不同模式的权重及消除了偏差,超级集合方法对于热带气旋路径及中心气压的预报效果较其他几种方案更好,为最优方案。
对于台风路径预报,其系统性偏差较难以把握,时而偏实况左侧时而偏实况右侧,使得消除偏差的作用不够明显,如何对这种不确定的偏差进行消除,今后需要进一步研究;另外,对超级集合方案中系统性偏差以及权重系数计算方法的改进,是今后工作的重点。
陈静, 薛纪善, 颜宏, 2005. 一种新型的中尺度暴雨集合预报初值扰动方法研究[J]. 大气科学, 29(5): 717-726. |
董海萍, 张秀丽, 郭卫东, 等, 2013. 2010年8月环流形势的多模式超级集合预报[J]. 应用气象学报, 24(5): 606-616. DOI:10.11898/1001-7313.20130510 |
林春泽, 智协飞, 韩艳, 等, 2009. 基于TIGGE资料的地面气温多模式超级集合预报[J]. 应用气象学报, 20(6): 706-712. DOI:10.11898/1001-7313.20090608 |
李佰平, 智协飞, 2012. ECMWF模式地面气温预报的四种误差订正方法的比较研究[J]. 气象, 38(8): 897-902. DOI:10.7519/j.issn.1000-0526.2012.08.001 |
刘永和, 严中伟, 冯锦明, 等, 2013. 基于TIGGE资料的沂沭河流域6小时降水集合预报能力分析[J]. 大气科学, 37(3): 539-551. DOI:10.3878/j.issn.1006-9895.2012.11078 |
谭燕, 梁旭东, 2010. 一次登陆台风的集合预报试验[J]. 热带气象学报, 26(4): 401-410. |
许映龙, 2011. 超强台风鲇鱼路径北翘预报分析[J]. 气象, 37(7): 821-826. DOI:10.7519/j.issn.1000-0526.2011.07.006 |
尤凤春, 魏东, 王雨, 2009. 北京奥运期间多模式降水检验及集成试验[J]. 气象, 35(11): 3-8. DOI:10.7519/j.issn.1000-0526.2009.11.001 |
张国华, 张江涛, 张南, 等, 2011. 基于河北区域天气分型的多模式降水检验评估[J]. 气象, 37(8): 968-976. DOI:10.7519/j.issn.1000-0526.2011.08.008 |
张涵斌, 陈静, 智协飞, 等, 2014. GRAPES区域集合预报系统应用研究[J]. 气象, 40(9): 1076-1087. DOI:10.7519/j.issn.1000-0526.2014.09.005 |
智协飞, 林春泽, 白永清, 等, 2009. 北半球中纬度地区地面气温的超级集合预报[J]. 气象科学, 29(5): 569-574. |
智协飞, 彭婷, 李刚, 等, 2014. 多模式集成的概率天气预报和气候预测研究进展[J]. 大气科学学报, 37(2): 248-256. |
周文友, 智协飞, 2012. 2009年夏季西太平洋台风路径和强度的多模式集成预报[J]. 气象科学, 32(5): 492-499. |
Goerss J S, 2000. Tropical cyclone track forecasts using an ensemble of dynamical models[J]. Mon Wea Rev, 128: 1187-1193. DOI:10.1175/1520-0493(2000)128<1187:TCTFUA>2.0.CO;2 |
Hagedorn R, Doblas-Reyes F J, Palmer T N, 2005. The rationale behind the success of multi-model ensembles in seasonal forecasting-I[J]. Basic concept.Tellus, 57A: 219-233. |
Krishnamurti T N, Gnanaseelan C, Chakraborty A, 2007. Forecast of the Diurnal Change Using a Multi-model Superensemble.Part Ⅰ: Precipitation[J]. Mon Wea Rev, 135: 3613-3632. DOI:10.1175/MWR3446.1 |
Krishnamurti T N, Kishtawal C M, LaRow T E, et al, 1999. Improved weather and seasonal climate forecasts from multi-model superensemble[J]. Science, 285: 1548-1550. DOI:10.1126/science.285.5433.1548 |
Krishnamurti T N, Kishtawal C M, Shin D W, et al, 2000a. Multi-model superensemble forecasts for weather and seasonal climate[J]. J Climate, 13: 4196-4216. DOI:10.1175/1520-0442(2000)013<4196:MEFFWA>2.0.CO;2 |
Krishnamurti T N, Kishtawal C M, Zhang Z, et al, 2000b. Improving tropical precipitation forecasts from a multi-analysis superensemble[J]. J Climate, 13: 4217-4227. DOI:10.1175/1520-0442(2000)013<4217:ITPFFA>2.0.CO;2 |
Krishnamurti T N, Rajendran K, Vijaya Kumar T S V, et al, 2003. Improved skill for the anomaly correlation of geopotential heights at 500 hPa[J]. Mon Wea Rev, 131: 1082-1102. DOI:10.1175/1520-0493(2003)131<1082:ISFTAC>2.0.CO;2 |
Leith C E, 1974. Theoretical skill of Monte Carlo forecasts[J]. Mon Wea Rev, 102: 409-418. DOI:10.1175/1520-0493(1974)102<0409:TSOMCF>2.0.CO;2 |
Molteni F, Buizza R, Palmer T N, et al, 1996. The ECMWF ensemble prediction system: Methodology and validation[J]. Quart J Roy Meteor Soc, 122: 73-119. DOI:10.1002/(ISSN)1477-870X |
Toth Z, Kalnay E, 1997. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 125: 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2 |
Vijaya Kumar T S V, Krishnamurti T N, Fiorino M, et al, 2003. Multimodel superensemble forecasting of tropical cyclones in the Pacific[J]. Mon Wea Rev, 131: 574-583. DOI:10.1175/1520-0493(2003)131<0574:MSFOTC>2.0.CO;2 |
Williford C E, Krishnamurti T N, Torres R C, et al, 2003. Real-time multimodel superensemble forecasts of Atlantic tropical systems of 1999[J]. Mon Wea Rev, 131: 1878-1894. DOI:10.1175//2571.1 |
Zhi X, Qi H, Bai Y, et al, 2012. A comparison of three kinds of multimodel ensemble forecast techniques based on the TIGGE data[J]. Acta Meteor Sinica, 26(1): 41-51. DOI:10.1007/s13351-012-0104-5 |
 2015, Vol. 41
2015, Vol. 41