引言

积云对流活动通过动力、热力等因素影响大尺度环流，并在决定大气温湿场的垂直结构中扮演着非常重要的角色，与大尺度天气系统有着密切的关系。另外，积云对流还与强降水的发生发展紧密相关，但对它的预报一直都是数值预报中的重要难点。因此近几十年以来，很多学者致力于积云参数化方案的研究(许习华，1991；陈德辉，1997；林文实等，1998；董美莹等，1999；左瑞亭等，2008；王德立等, 2013)。但是积云的典型尺度在一般的数值模式中是属于次网格过程，要使这种对流过程能够被模式可分辨的网格尺度所表达，模式必须将其参数化。由此而产生积云参数化方案，它是在大气环流模式或数值天气预报模式中，用大尺度可分辨的模式变量来描述属于次网格尺度物理过程的积云对流效应的方法。从提出积云对流参数化方案到目前为止，它在理论方面发展的已较为完善，许多具有代表性的参数化方案被提出并且产生了重要影响。如Betts-Miller，Kuo，Arakawa-Schubert和Tiedtke，Kreitzberg-Perkey，Fritsch-Chappel和Kain-Fritsch方案等(Frank, 1983; 1987;Betts, 1986; Kain et al, 1990; 1993;Arakawa et al, 2004; Anderson et al, 2007)。本文着重讨论GRAPES区域中尺度模式中主要积云参数化方案Betts-Miller-Janjic和Kain-Fritsch Eta方案在预报性能上的差别，选择2009年冬季(1月)和2009年夏季(6—8月)进行批量回报试验，比较两种方案的预报性能，为以后方案的改进提供依据。

1 GRAPES_Meso及两种参数化方案介绍 1.1 GRAPES_Meso区域中尺度模式

GRAPES(Global/Regional Assimilation and PrEdiction System)是中国气象局的科研人员自主研究发展的以动力模式为核心的、多尺度通用(全球区域一体化)的新一代数值预报模式系统。2006年，水平分辨率为30 km的GRAPES_Meso在中央气象台正式投入了业务运行，2007年水平分辨率提升到15 km，经多年的发展已表现出较好的预报效果(陈德辉等，2008; 2012)。该模式采用完全可压缩的非静力学方程组；时间积分使用半隐式半拉格朗日方案；水平方向为球面坐标，垂直方向采用地形追随高度坐标；空间离散化时，模式水平方向采取Arakawa-C跳点经纬网格，垂直方向取Charney-Phillips变量配置(伍湘君等，2005；薛纪善等，2008；张人禾等，2008)。本文试验采用GRAPES_Meso V3.3.2.4最新版本。

1.2 Betts-Miller-Janjic方案

BMJ方案是一种同时包含深浅对流的对流调整式方案，Betts-Miller方案(Betts，1986)中的深对流温度调整参考廓线取修正的湿绝热线或“观测的准平衡状态线”、浅对流温度调整参考廓线使用“混合线”。之后Janjic(1994)为了解决Betts-Miller方案在实际模拟中出现的一些虚假降水，在Betts-Miller方案温度调整参考廓线的基础上再引入积云效率来表示对流组织的性质，熵的变化、降水量和云的平均温度决定了积云效率，积云效率参数又决定了深对流参考廓线和松弛调整时间。而浅对流湿度参考廓线是要求熵的变化最小且非负。新形成的Betts-Miller-Janjic方案(以下简称BMJ方案)在许多数值模式中都表现出不俗的模拟效果。

1.3 Kain-Fritsch Eta方案

Kain-Fritsch方案是Kain等(1990；1993)基于Fritsch-Chappell方案(Fritsch et al, 1980)的闭合假设，通过修改云模式(可变云半径和云深)和夹卷效应而形成。Kain(2004)之后又通过引入浅对流过程、修改下沉气流以及设定夹卷率最小阈值对Kain-Fritsch方案进行了改进，改进后的方案称为Kain-Fritsch Eta方案(以下简称KFeta方案)。此方案中深对流以假定在一定时间内消耗约90%的对流有效位能，模式中的上升、下沉气流以及环境空气才会重新调整作为闭合假设，并采用简单云模式来判定积云对流和网格尺度的相互关系。该方案从地面开始，依次以垂直厚度至少为60 hPa的气层作为升源层(updraft source layers，USL)，将气块从USL抬升至抬升凝结高度(LCL)，计算在该高度处的温度(T_LCL)，通过比较抬升凝结高度处气块温度(包括实际温度T_LCL和扰动温度ΔT)和环境温度(T_ENV)的高低来判定上升气流起始高度，上升气块通过浮力机制和环境相互作用，若上升气块未达到最低云高，则判定下一个USL，若达到，则启动深对流。方案中的对流降水同时计算了气流上升、下沉过程中的卷入、卷出等过程。

2 试验设计及检验方法

本文为比较BMJ和KFeta方案在预报性能上的差异，设计了如下试验方案。选取2009年冬季1月和2009年夏季6—8月进行回报试验。回报试验的初始场和侧边界采用NCEP提供的2009年1和6—8月的时间间隔为3 h的GFS预报场，模式预报场区域为15°~65°N、70°~145°E，空间分辨率为0.15°×0.15°，预报时长为48 h，积分步长为90 s，微理过程方案为WSM6方案、边界层方案为MRF方案、短波辐射为Dudhia方案、长波辐射为RRTM方案、近地面层方案为Monin-Obukhov方案、陆面过程方案为Noah方案、积云参数化方案采用KFeta方案和BMJ方案。

对试验结果进行统计检验的方法主要有误差统计检验和TS评分(狄靖月等，2013；张涵斌等，2014；毛冬艳等，2014)。误差统计的范围为整个预报场区域，观测场资料采用NCEP的2009年1和6-8月的FNL逐日再分析资料，要素包括高度、温度、风场u分量和v分量、相对湿度。空间分辨率为1°×1°，垂直方向取200、500和850 hPa共3层，分别代表大气的高、中和低三个层次。统计量主要为平均值和均方根误差(RMSE)，两个方案的差异显著性检验采用适用于小样本检验的t检验方法。TS评分统计检验采用国家气象中心预报质量评分系统的降水预报累加检验方案, 把24 h累计降水分为小雨(≥0.1 mm)、中雨(≥10 mm)、大雨(≥25 mm)、暴雨(≥50 mm)及特大暴雨(≥100 mm)五级，进行累加降水检验。即小雨累加检验为小雨以上所有量级降水(包括小雨、中雨、大雨、暴雨、特大暴雨)统计结果的累加，中雨累加检验为中雨以上所有量级降水统计结果的累加，以此类推。

3 试验结果误差统计分析 3.1 2009年1月试验结果

对两个方案在2009年1月(图略)回报结果进行了误差统计(熊秋芬，2011)。统计时，在850 hPa等压面上去除了地形以下的点，从而去除了外插数据的影响。统计结果表明，两个方案在高层(200 hPa)的均方根误差约为10~30 gpm，在中低层(850和500 hPa)的高度场均方根误差约为6~16 gpm，但两个方案在各层均方根误差的差值约为±0.1 gpm，没有通过α=0.05的显著性水平检验，表明两个方案之间没有明显差异。对于温度场而言，两个方案在低层误差大些，均方根误差约为1.2~2.1℃，在中高层的温度场均方根误差则约为0.8~1.7℃，两个方案的差值约为±0.01℃，表明两个方案之间差异较小。就风场(u和v分量)而言，在低层的均方根误差约2.1~3.2 m·s^-1，在高层稍大些，为2.5~4.3 m·s^-1，但两个方案的均方根误差之间的差值为±0.02 m·s^-1，两个方案之间的差异也较小。湿度场统计结果表明各个层次的均方根误差约为14%~24%，但两个方案的均方根误差之间的差值约为0.2%，两个方案之间的差异也不明显。

综上所述，在预报场区域内由于冬季的对流活动比较少，所以两个方案对GRAPES_Meso模式的预报性能的影响差异并不显著。

3.2 2009年6—8月试验结果

对两个方案在2009年夏季6—8月预报结果进行了误差统计。统计时，同样在850 hPa等压面上去除了地形以下数据的影响。

3.2.1 高度场

从平均误差的统计结果来看(图略)，随着预报时效的延长(预报时效从12 h到48 h)，在高层(200 hPa)，KFeta方案的平均误差从-1 gpm增长到12 gpm，BMJ方案则从-3 gpm增长到9 gpm，KFeta方案要比BMJ方案高2~3 gpm；在中层(500 hPa)，两个方案的误差平均值都是小于零，预报高度场比观测场偏低4~10 gpm，但KFeta方案比BMJ方案高2~3 gpm；在低层(850 hPa)，两个方案的误差平均值都是小于零，预报高度场比观测场偏低6~20 gpm，然而KFeta方案比BMJ方案低0~1.5 gpm。

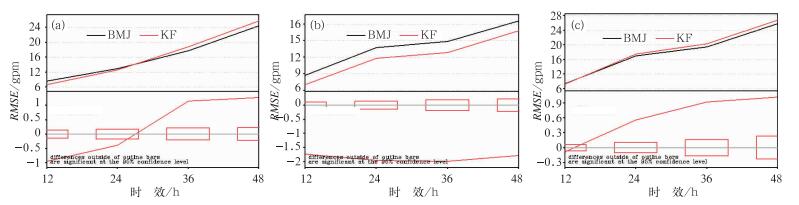
图 1是2009年夏季6—8月的两个方案的高度均方根误差平均图。从图中可以看出，两种方案在高层(200 hPa)24 h之前是KFeta方案误差相对较小，24 h之后则是BMJ方案较小；在中层(500 hPa)则是KFeta方案明显好于BMJ方案，通过α=0.05的显著性水平检验；低层(850 hPa)则是BMJ方案略好于KFeta方案，通过α=0.05的显著性水平检验。

由此可知，KFeta方案在中层的预报效果明显优于BMJ方案，但在低层却不如BMJ方案。

3.2.2 温度场

从平均误差的统计结果来看(图略)，在高层KFeta方案的平均误差从0.16℃演变成-0.09℃，BMJ方案则从0.13℃演变成-0.22℃；在中层和低层，两个方案的温度平均误差均大于0，预报的温度都比实况偏高。同时，在各个层次上，KFeta方案温度偏差都比BMJ方案的温度偏差偏高0.12℃。

图 2是2009年夏季6—8月的两个方案的温度均方根误差平均图。从图中可以看出，两种方案在中、高层24 h之前是KFeta方案误差相对较小，24 h之后则是BMJ方案较小；低层(850 hPa)则在12 h后，BMJ方案一直都略好于KFeta方案，通过α=0.05的显著性水平检验。

由上面的分析可知，KFeta方案预报的温度偏高，在中高层的预报前24 h效果比BMJ好，但在24 h后，以及在低层的预报都不如BMJ方案。

3.2.3 风场

从平均误差的统计结果来看(图略)，在高层两个方案的风场u分量的平均误差都比实况偏小，KFeta方案比BMJ方案偏小得多一些；两个方案的风场v分量都比实况偏大，但两个方案之间的差异不显著。在中层，风场u和v分量总体上都是比实况偏大，但KFeta方案的风场u分量平均误差总比BMJ方案大，风场v分量的偏差比BMJ方案小。在低层，风场u和v分量总体上均比实况偏大，但KFeta方案的风场u分量平均误差总比BMJ方案大，风场v分量的偏差与BMJ方案没有明显的区别。

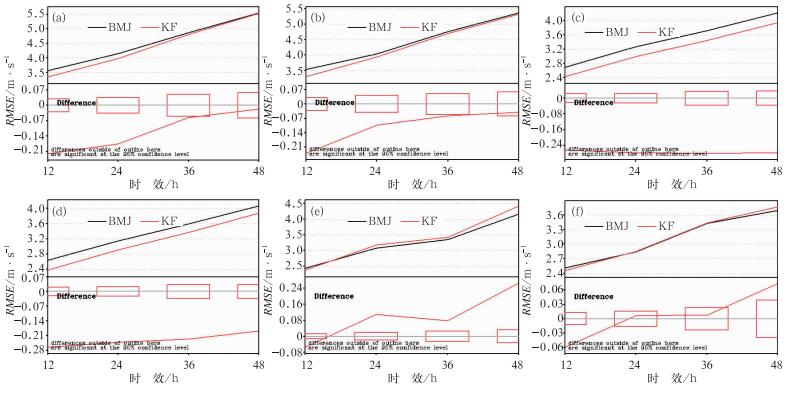
图 3是2009年夏季6—8月的两个方案的风场(u和v)均方根误差平均图。从图中可以看出，在高层(图 3a和3b)KFeta方案预报效果较好，在36 h之前差异是显著的。在中层(图 3c和3d)KFeta方案的误差略小于BMJ方案。在低层(图 3e和3f)KFeta方案的风场u分量误差大于BMJ方案，效果不如BMJ方案，风场v分量两个方案相当。

由此可知，KFeta方案预报风场在高层和中层的误差明显比BMJ方案小，然而低层的预报效果则不如BMJ方案。

3.2.4 相对湿度

两个方案相对湿度的平均误差表明(图略)，在高、中、低各层都比实况偏干。然而在高层KFeta方案比BMJ方案要好些，在中层和低层KFeta方案比BMJ方案更干，效果不如BMJ方案，均通过了α=0.05的显著性水平检验。

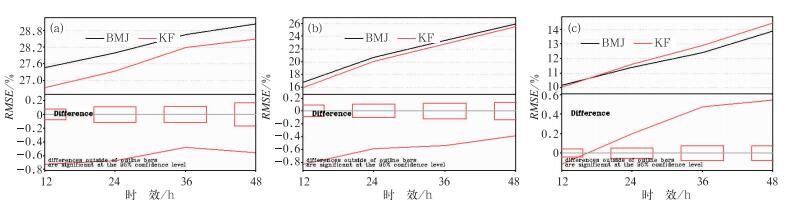
图 4是2009年夏季6—8月的两个方案的相对湿度均方根误差平均图。从图中可以看出，在高层和中层(图 4a和4b)KFeta方案的误差小于BMJ方案误差，回报效果较好。而在低层(图 4c)KFeta方案的误差大于BMJ方案误差，回报效果比BMJ方案差, 均通过了α=0.05的显著性水平检验。

4 降水检验

根据前面的分析，可知两个方案在冬季对GRAPES_Meso模式的回报效果的影响差异不明显。因此，本节仅对对流活动比较活跃的6—8月的降水回报效果进行对比分析。

4.1 空间TS评分检验

采用国家气象中心预报质量评分系统的降水预报累加检验方案, 对预报的降水进行累加降水检验。图 5给出了KFeta和BMJ两种对流参数化方案的24和48 h预报降水的TS评分和系统偏差在6—8月的平均值。从TS评分图(图 5a和5b)中可以看出，在小雨量级两个方案的24和48 h预报降水的TS评分相当，但KFeta方案预报的降水在24和48 h小雨以上各个量级的TS评分都比BMJ方案高。从系统偏差上来看(图 5c和5d)，两个方案的24和48 h的小雨预报范围与实况很接近，中雨到暴雨量级则是预报范围偏小，漏报比较多，但KFeta方案比BMJ方案要好，更接近实况。特大暴雨的预报范围都偏大，空报比较多，KFeta方案空报相对更多。

4.2 时间系列TS评分检验

为了了解两个参数化方案对降水回报效果差异的空间分布，本小节对我国范围内的2513个观测站中每个站点的时间序列进行了TS评分检验。检验方法参考国家气象中心的空间检验方法，将检验时段(2009年夏季6—8月)中的92 d数据当成92个站点数据，分别统计它们的TS评分值。同样把24 h累计降水分为小雨(≥0.1 mm)、中雨(≥10 mm)、大雨(≥25 mm)、暴雨(≥50 mm)及特大暴雨(≥100 mm)五级。通过以上方法，可以得到两个参数化方案预报降水的全国2513个站点不同降水等级的TS评分值。

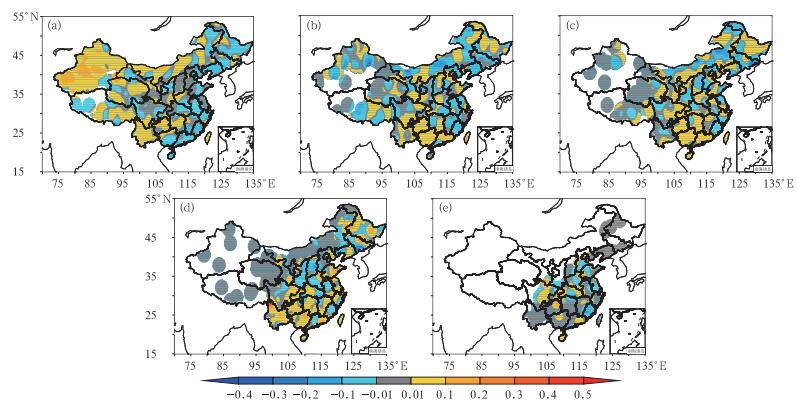
图 6是两个参数化方案夏季24 h预报的24 h累积降水TS评分差值分布。由于是数据站点形式，所以这里先计算各个站点上的差值，然后采用GrADS绘图软件的Cressman插值方法插值到GRAPES_Meso模式的模拟格点上，得到格点化的差值。其中，Cressman插值的扫描半径r=24，20，16, 14，12，分别相当于360, 300，240，210和180 km。从图 6中可以看出在小雨量级上，虽然总体上两个方案TS评分相当，但从空间分布上看KFeta方案在110°E以西有优势，但在110°E以东则不如BMJ方案。在中雨到暴雨量级上，KFeta方案在华南有明显的优势。在中国西部，由于降水量较小，往往达不到大雨量级，所以在大雨及以上量级上两个方案的差异较小甚至没有差别，其差异主要在我国的东部。特大暴雨量级的差异则主要在中东部，有好有坏，有很强的局地性。

4.3 积云降水贡献率分析

在数值模式GRAPES_Meso预报的降水中，降水总量是积云降水量和格点降水量的总和。不同积云对流参数化方案因触发机制和计算过程都不同，这种不同便造成了在预报区域降水时不同积云对流参数化方案的选择会对积云降水量的计算造成不同的结果。为进一步讨论两种方案对预报降水效果的影响，本小节主要关注积云参数化方案在预报时对总降水所做的贡献，计算了积云降水在总降水中的比例。同时，获取了ECMWF的2009年6—8月(year of tropical convection，YOTC)逐日降水预报资料，使用的资料区域范围为15°~65°N、70°~145°E，空间分辨率为0.225°×0.225°，计算了积云降水在总降水中的比例。

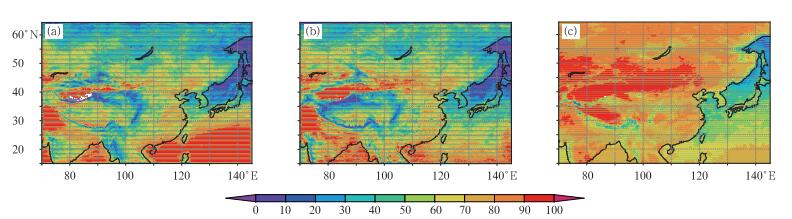
图 7给出了2009年夏季(6—8月)GRAPES_Meso的BMJ、KFeta方案以及YOTC模式的24 h预报积云降水在总降水中比例平均值的空间分布。平均值的计算方法是先计算每一天预报的积云降水在总降水中的比例，然后统计92 d的平均值。从图中可以看出，GRAPES_Meso的两个参数化方案预报积云降水平均贡献率的空间分布趋势基本一致，在陆面和洋面上都有明显的高纬度值小、低纬度值大的趋势。另外，在地形陡峭的青藏高原边缘也出现小值区。而YOTC的资料显示，除了在中纬度有一条高值带外，在陆面上并没有明显的纬度变化，降水以积云对流降水为主。在洋面上，YOTC资料也没有GRAPES_Meso模式表现得那么极端。GRAPES_Meso模式的两个参数化方案的积云参数化方案之间的差别主要表现在低纬度的洋面上。BMJ方案在低纬度洋面上几乎没有格点降水，而KFeta方案的积云对流降水则在80%左右。

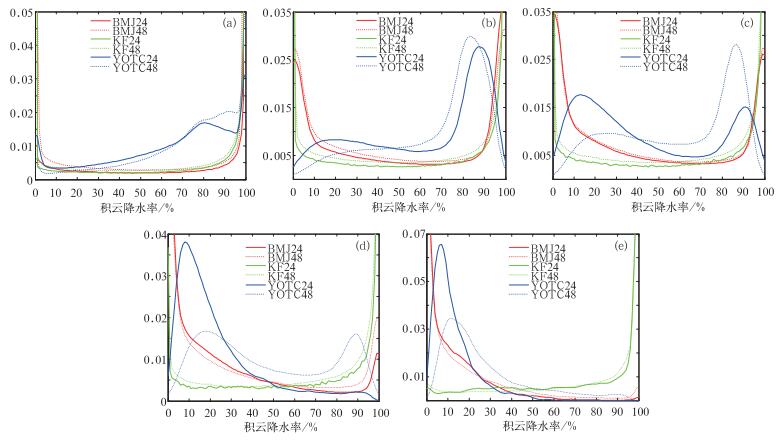
图 8给出了2009年夏季(6—8月)GRAPES_Meso的BMJ、KFeta方案和YOTC资料的24 h预报积云降水在总降水中比例的各个量级概率分布。统计时没有求平均，而是直接统计各个量级的92 d的所有格点上的比例值，利用Matlab软件中的ksdensity函数进行计算。从总体上看，图 8表明不同预报时效的概率分布形态相似，预报时效对贡献率的影响远小于不同方案和不同模式的影响。GRAPES_Meso的两个积云参数化方案的积云降水贡献率的概率分布形态在小雨量级上均呈陡峭的“U”字型分布。其中，KFeta参数化方案随着降水量级的增大逐渐向大贡献率偏移，特大暴雨量级时基本上是积云降水的贡献；而BMJ参数化方案则是随着降水量级的增大逐渐向小贡献率偏移，特大暴雨量级时基本上是格点降水的贡献。相比而言，EC的模式则没有陡峭的“U”型分布，在小雨量级80%处还有一个峰值，在中到暴雨量级演变成双峰形态，分别对应于10%~20%和80%~90%，特大暴雨量级则又演变成在10%处的单峰型。

因此，积云降水贡献率的概率分布形态表明，GRAPES_Meso模式的总降水要么90%以上是有积云参数化过程产生的，要么90%以上是有显示微物理过程产生的，积云参数化方案与显式微物理方案之间的协调性较差。从各个降水量级的形态演变趋势方面来看，BMJ方案与YOTC资料接近，都是随着降水量级的增大逐渐向小比例值方向偏移，即格点降水的贡献率逐渐增大。

5 结论

本文基于GRAPES_MesoV3.3.2.4版本，通过对2009年冬季(1月)和夏季(6—8月)的批量回报试验，分析了BMJ和KFeta两种积云对流参数化方案的回报性能，并详细分析了两种参数化方案对模式预报降水的影响，得到的主要结论如下：

(1) 由于冬季的对流活动比较少，所以两个方案对GRAPES_Meso模式的预报性能的影响差异非常小。

(2) 从形势场误差统计来看，夏季在模式的低层BMJ方案略优于KFeta方案，中层则是KFeta方案明显优于BMJ方案，而在高层KFeta方案略优于BMJ方案。

(3) 两个方案在夏季预报降水小雨量级24和48 h的TS评分相当；小雨以上量级，KFeta方案预报的降水在24和48 h的TS评分都比BMJ方案高，预报范围比BMJ方案更接近实况。虽然两个参数方案在小雨量级的TS评分总体上相当，但在空间分布上却有明显的差异。KFeta方案在110°E以西有优势，但在110°E以东则不如BMJ方案。在中雨到暴雨量级上，KFeta方案在华南有明显的优势。在中国西部，由于降水量较小，往往达不到大雨量级，所以在大雨及以上量级上两个方案的差异较小甚至没有差别，其差异主要在我国的东部。特大暴雨量级的差异则主要在中东部，有好有坏，有很强的局地性。

(4) 两个参数化方案预报积云降水平均贡献率的空间分布趋势基本一致，在陆面和洋面上都有明显的高纬度值小、低纬度值大的趋势。另外，在地形陡峭的青藏高原边缘也出现小值区。两个方案之间的差别主要表现在低纬度的洋面上，BMJ方案的贡献率比KFeta方案大。与YOTC资料相比，GRAPES_Meso的对流参数化方案对流触发机制相对较弱，对流过程的维持机制有些过强。而KFeta方案在低纬度的洋面上则比BMJ方案要好一些。

(5) 两个方案积云降水贡献率的概率分布形态在小雨量级上均呈陡峭的“U”型分布。其中，KFeta参数化方案随着降水量级的增大逐渐向大贡献率偏移，特大暴雨量级时基本上是积云降水的贡献；而BMJ参数化方案则是随着降水量级的增大逐渐向小贡献率偏移，特大暴雨量级时基本上是格点降水的贡献。相比而言，YOTC资料则没有陡峭的“U”型分布，而是呈单峰或双峰形态。从形态演变趋势方案来看，BMJ方案与YOTC资料接近。

6 讨论

相对于BMJ方案，KFeta方案考虑了积云的卷入、卷出效应，并且考虑了积云对流过程对大气环境的风场的作用，因此在大气的中高层，KFeta方案对大气温、湿和风场的调整效果比BMJ方案好，误差变小。这可能是在总体上KFeta方案对形势场和降水的预报性能比BMJ方案略好的主要原因。通过时间系列TS评分检验，发现BMJ方案对降水(尤其是小雨量级)预报在东部沿海地区有优势，而在我国西部的内陆地区则不如KFeta方案。这说明由于BMJ方案的调整参考廓线是使用热带海洋大气试验观测资料得到的修正的廓线湿绝热线，比较适合在热带或者沿海地区，在我国的内陆地区则不太适合，使用BMJ方案时可能需要进一步做本地化的调整。相对而言，KFeta方案的普适性要强些。

BMJ方案在对流调整过程中对对流产生的凝结、感热和潜热的垂直输送可以不用显式方法表示出来，而是估算其总的作用，给出调整后的最终状态。该方案具有计算简单的特点，但在方案调整完成的瞬间，对模式的冲击较大，容易产生过度的降水。从图 7中可以明显地看出，BMJ方案(图 7a)在洋面上的积云降水比KFeta方案(图 7b)明显偏强，其主要原因就是由BMJ方案的对流调整机制造成的。

将图 7a和7b与图 7c的YOTC资料相比，GRAPES_Meso的积云降水和格点降水的协调性不好，要么全部是积云过程的降水，要么全部是微物理的格点降水，这可能与方案本身的设计有关。其中，YOTC的数值模式中使用质量通量式积云参数化方案，方案采用了准平衡闭合假设，积云对流描述得比较仔细，考虑了云和云之间以及云和大尺度环境之间彼此相互作用，并且显示出与边界层强烈的相互作用。该积云参数化方案与模式的其他物理过程之间的协调性较好，因此积云降水过程是微物理格点降水过程的有效补充。另一方面，就KFeta方案而言，该方案中需要用到一个滑动平均垂直速度(W_0AVG)，其值取初始为零，那么用垂直速度(w)计算第一步的W_0AVG时，它的值为w/2，之所以用W_0AVG代替瞬时的垂直速度是为了用更加平滑的垂直速度计算局地温度扰动，进而判断对流初始激发(邓华，2008)。因为此方案的初始激发条件相对严格，因而可能会造成对流不容易被激发出来。一旦对流被激发出来后，由于对流有效位能(CAPE)在一定的调整时间内立即被释放。这可能是GRAPES_Meso的两个方案积云降水贡献率的概率分布形态呈陡峭的“U”型或“L”型分布的原因之一。当然，积云降水的分布特征还有可能与其他的一些因素有关，如数值模拟初值场的选取，不同类型降水过程等，这还有待进一步的研究。