引言

暴雨洪涝是最重要的气象灾害之一，20世纪90年代以来我国暴雨洪涝灾害频数和受灾程度明显增加(秦大河，2007)。受气候变化影响，未来全球洪涝灾害发生的风险将会进一步上升(Nicholls et al，1999；Milly et al，2002; 2005)，包括我国部分地区如江淮流域等(田红等，2008)。因此，防范暴雨洪涝灾害对保障社会经济持续发展具有重大意义。

致灾影响阈值(简称致灾阈值，disaster inducing threshold)是指天气气候灾害发生时的临界天气气候条件，达到这一临界条件时，天气气候灾害就造成生命伤亡或社会经济财产损失(Martina et al，2006；章国材，2012；高超等，2014)。例如暴雨洪涝灾害的发生与该时刻前逐时或逐日的累积降水量密切相关，可以用致灾临界雨量来表示。致灾临界雨量是暴雨灾害预报、预警、评估以及防治规划的重要依据和参考。在以往的研究中，致灾临界气象条件所引起的重视远远不够，相关的研究基础也较为薄弱。随着气象灾害风险研究的深入，一些新的理念和技术方法也在不断的涌现(章国材，2012；彭涛等，2014；李建通等，2015)，如流量反推法(叶勇等，2008；樊建勇等，2012)、二维水动力模型法(文明章等，2013；张容焱等，2013)和基于前期土壤含水量的动态指标法(叶金印等，2014)等。上述研究在临界雨量求算方法方面进行了有益的探索，并且提供了一些行之有效的方法。然而这些研究大多着眼于小尺度、短历时的突发性山洪灾害，对于汇水面积大、产汇流过程较长的流域洪水的研究尚不多见。

不同于源短流急的山洪，流域洪水的致灾机制更为复杂，研究其临界雨量还需进一步考虑前期流域的湿润程度和河道水位顶托等因素影响。随着水文气象耦合技术的发展，水文模型为确定流域洪水的临界雨量提供了重要的技术手段。流域水文模型是对自然界中复杂水文现象作近似的模拟(赵琳娜等，2012；翟丹华等，2015)，能够模拟降水致洪过程，建立适用于研究区域的暴雨洪水定量响应关系，从而通过雨-洪-灾三者的关系来最终确定致灾临界面雨量。

为探索流域洪水的致灾临界雨量确定方法，本文选取淮河王家坝以上流域作为研究区域，以半分布式水文模型HBV为基础，利用历史气象和水文资料，建立了一种动态临界雨量指标的计算方法。

1 研究区概况与致灾条件识别

淮河流域地处南北气候交绥处，旱涝易发，并且由于淮河上游流域地势高、落差大、降水下泄快，中游地势平坦、落差小、水流缓慢，下游没有直接出海口，淮河流域集中强降水极易导致洪涝灾害的产生(矫梅燕等，2008)。王家坝位于淮河上、中游结合部，王家坝以上淮河长约360 km，集水面积30630 km²，河道比降万分之五。王家坝是淮河中游的门户，洪水首当其冲，并且其上游山区坡度陡，水库拦蓄相对较小，河道调节能力差，导致王家坝洪水易暴涨暴落。

王家坝历经14次开闸蓄洪，蒙洼蓄洪区饱受洪灾危害，对于王家坝地区而言，暴雨致灾主要是由于流域内降水致洪，使河道水位上涨，超过一定水位时需要分洪，导致蓄洪区被淹、人民生命财产受损等。因此，临界面雨量可通过河流控制断面的防洪标准等级来进行判别，当王家坝以上流域内降水致使该站河流水位上涨至警戒、保证水位，这时的流域面雨量就分别对应不同等级洪水临界(面)雨量。

2 资料与方法 2.1 数据资料

气象数据来自流域内气象站逐日观测资料，包括降水和气温。水文数据采用的王家坝水文控制站逐日流量和水位资料。数字地面高程(DEM)为90 m分辨率的SRTM数据，土地利用数据来源于1：100000土地利用基础数据集。气象、高程和土地利用数据用于驱动HBV模型，水文数据用于模型率定和验证。

以DEM和水系分布为基础，采用GIS水文分析工具将王家坝以上流域分为34个子流域，图 1为气象站、水文站分布情况以及划分好的子流域，采用Kriging法得到各子流域逐日面雨量。

2.2 HBV模型

HBV模型是一个概念性、半分布式的流域水文模型(Bergstrom，1976)，由瑞典气象水文研究所研发，该模型已在世界40多个不同气候条件的国家中得到成功应用。根据以往的应用案例，HBV能够适应于各种复杂气候条件下的水文模拟，同时具有输入参数少、适用性强和模拟精度高等优点。HBV模型在我国也有较好的应用范例(刘绿柳等，2012；刘学锋等，2013)，从模拟结果看，该模型具有较好的区域适应性，因此选用该模型作为研究的分析工具。

HBV模型综合考虑了降水、气温、土壤和产汇流等要素，进而对径流进行模拟或预测，该模型以子流域为模拟单元，根据地形和下垫面的空间差异，分别模拟各子流域径流过程，最后汇总到流域出口断面(姜彤，2013)。

模型输入数据为日降雨量、气温和月潜在蒸发量，输出为日径流深。模型包括降水模块(由日温度方法来划分降水、积雪和融雪)、土壤模块(地下水补给和实际蒸发通过实际土壤蓄水量的函数计算求得)、产汇流模块(用三个线性水库方程描述)和一个河道模块。模型参数包括了积雪和融雪参数、温度阈值参数、田间持水量、退水系数及河道参数等30余个具有物理意义的参数，可以通过优化调整参数，使模型在率定期内达到拟合最优。

为判别HBV模型模拟效果，采用确定性系数(R²)和NASH效率系数(ME)来分别度量均值和极值的模拟效果。

$ \begin{array}{l} {R^2} = \frac{{{{\left[ {\sum {\left({{Q_{{\rm{obs}}}} - {{\bar Q}_{{\rm{obs}}}}} \right)\left({{Q_{{\rm{sim}}}} - {{\bar Q}_{{\rm{sim}}}}} \right)} } \right]}^2}}}{{\sum {{{\left({{Q_{{\rm{obs}}}} - {{\bar Q}_{{\rm{obs}}}}} \right)}^2}\sum {{{\left({{Q_{{\rm{sim}}}} - {{\bar Q}_{{\rm{sim}}}}} \right)}^2}} } }}\\ ME = 1 - \frac{{\sum {{{\left({{Q_{{\rm{obs}}}} - {Q_{{\rm{sim}}}}} \right)}^2}} }}{{\sum {{{\left({{Q_{{\rm{obs}}}} - {{\bar Q}_{{\rm{obs}}}}} \right)}^2}} }} \end{array} $

式中，Q_obs和Q_obs分别为观测值及观测值平均；Q_sim和Q_sim分别为模拟值及模拟值平均，R²和ME取值范围在0~1，越接近1，模拟效果越好。

3 模型适用性分析

将2003—2009年流域气象水文观测数据分成率定期(2003—2006年)和验证期(2007—2009年)，其中率定期数据用于确定模型参数，验证期数据用于检验模型参数适用性和模拟效果。由于本文研究对象主要为致灾雨量和洪水，相比于一般水文模型的参数确定，本研究更加关注模型对洪峰流量的模拟，因此，首先利用逐日气象水文数据初步确定模型参数，之后选取典型洪水过程对参数进行优化，使模型模拟的洪水过程及洪峰流量与实测更为接近。

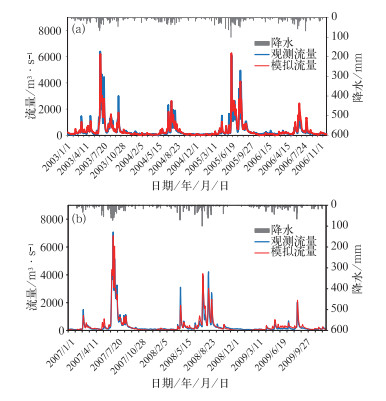
经过模型率定后，可以看出HBV模型能够较好地反映流域内降水径流过程，在率定期内实测与模拟径流过程的趋势基本一致(图 2a)，模型的确定性系数达0.91，NASH效率系数为0.88，模拟效果较好。采用实测资料进一步对HBV模型的模拟效果进行了验证分析，可以看出验证期结果与率定期基本一致，验证期模拟的确定性系数为0.95，NASH系数为0.93，模拟的水文过程线与实测基本吻合(图 2b)。

从图 3可知，HBV模型对洪水过程具有较强的模拟能力，对2003、2005、2007和2008年淮河洪水过程的模拟基本与实测结果一致，模拟的确定性系数和NASH系数均在0.8以上，能够很好地模拟出洪水对降雨的响应过程。因此，经过率定后的HBV模型在王家坝以上流域具有很强的适用性，能够作为流域洪水致灾临界雨量的研究工具。

4 致灾临界雨量的确定 4.1 降水-流量-水位关系

通过HBV模型可以建立降水与径流量(或径流深)的响应关系，然而判断河道洪水是否致灾的直接指标则是水位，因此还需要进一步研究流量与水位的联系，从而以流量为纽带构建降水-流量-水位的对应关系，并作为确定致灾临界雨量的依据。

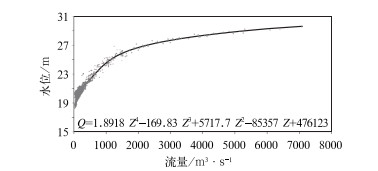
一般地，受洪水涨落影响的水位流量关系多呈复杂的绳套关系曲线(高兵役等，1998)，而本研究主要对象为致洪降水，因此这里只考虑水势上涨时水位流量关系，点绘相应时刻的水位-流量关系散点，概化为单一关系曲线(图 4)。

4.2 不同等级的动态临界雨量指标

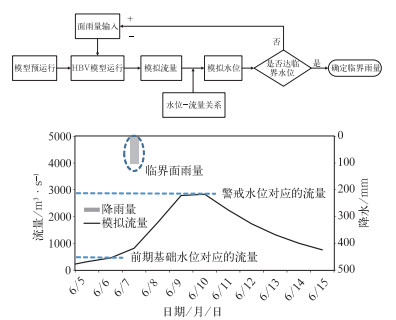
由于流域暴雨灾害发生是气象、地形地貌、下垫面类型和工程设施等多个要素共同作用的结果，因此，流域暴雨洪涝灾害的致灾临界气象条件不是一个静态的值，而是与前期水文特征、水利设施及下垫面等条件密切相关的动态条件(章国材，2012)。而在具有了适用于研究区域的降水径流模型后，就可以根据典型的灾害案例和防洪设施标准来推演出该区域的致灾临界气象条件。以王家坝为例，由于流域临界雨量与前期水文特征有关，当已知前期水位的情况下，即可根据所确定的降水-流量-水位关系来得到动态临界雨量值。计算步骤如图 5所示，采用HBV模型来反算临界面雨量：(1) 首先模型预运行使得河流上涨到一定水位，即前期基础水位；(2) 在达到基础水位后，给定一个面雨量值，输入HBV模型进行流量模拟，得到洪峰流量值；(3) 将模拟的洪峰流量代入到水位流量关系中得到模拟水位；(4) 将模拟水位与临界水位进行比较，如果同临界水位相差较大，那么重新给定面雨量进行模拟；(5) 通过多次调整雨量进行模拟，直到模拟水位与警戒或保证水位一致，此时得到的面雨量就是临界面雨量。

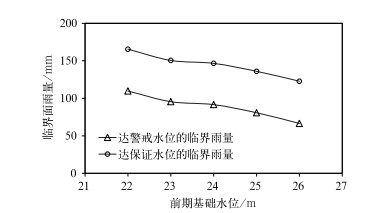
以王家坝断面警戒水位27.5 m和保证水位29.3 m分别作为不同等级的临界条件判据，采用上述分析方法计算了对应不同前期基础水位的各等级临界雨量指标(图 6)。根据流域自身特点和HBV模型的模拟步长，以24 h累积降水量作为临界雨量时效，以设定雨量的前一天水位为前期基础水位。由图 6可以看出临界雨量值随前期基础水位升高而减小，即当河流水位处于高位时，流域内土壤总体较为湿润，持水能力变小，这时即使较小的降水量也有可能导致河流出现灾害性洪水。同时，临界雨量随不同前期水位的变化呈现明显非线性的动态响应趋势(图 5)，这也体现了河流水文过程的非线性特征(李向阳等，2006)。

5 结论

致灾临界雨量是暴雨灾害风险预警和评估业务中重要的参考判据。根据流域暴雨洪水致灾机制，本文提出了考虑前期基础水位的动态致灾临界雨量指标，并以HBV水文模型为基础，通过考虑降水-径流-水位关系建立了临界雨量确定的方法流程。

以淮河上游地区为例，经过率定后的HBV模型对王家坝以上流域具备较好的适用性，能够很好地模拟出洪水对降雨的响应过程，可作为致灾临界气象条件的表征工具。HBV模型输入简单，使用气象数据即可驱动模型计算河流的水文特征量，为模型的应用以及临界雨量的推算提供了便利。通过模型反算结合水位流量关系得到了王家坝以上流域的动态致灾临界雨量指标，临界雨量随不同前期水位的变化呈现非线性的响应特征。

由于本文侧重于方法研究，所选流域相对较大，如将流域进一步细分，进行逐级模拟分析所得结果可更为精确合理。同时，限于模型模拟步长，目前临界雨量时效仅为日雨量，对次洪过程的拟合还欠缺一定的精细程度，在这方面有待进一步研究。