2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081;
3. 中国船舶重工集团第七二四研究所,南京 210003
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081;
3. No.724 Research Institute of CSIC, Nanjing 210003
中尺度对流系统(Mesoscale Convective Systems, MCSs)是造成暴雨、冰雹、大风等灾害性天气的主要天气系统原因之一(贝耐芳等,2002;张小玲等,2004;俞小鼎等,2008),给人们的生活生产带来极大的不便,甚至威胁人们的生命财产安全。如2004年上海“7.12”飑线带来的大风、龙卷和强降水、2011年南京“7.18”特大暴雨和2012年北京“7.21”特大暴雨(俞小鼎,2012;方翀等,2012;王婧羽等,2014),均造成严重的灾害和经济损失。因此,对MCSs进行预警和临近预报及其活动规律研究是十分重要的。
雷达资料具有时空分辨率高和覆盖范围广的优点,因此在MCSs的研究中被广泛应用。孙虎林等(2011)使用雷达拼图资料和多种其他资料研究了2009年6月3-4日发生的黄淮地区强飑线天气过程,雷达拼图资料很好地展现了强飑线的完整回波结构。易笑园等(2011)利用雷达拼图资料和多种其他资料研究了2007年7月18日华北东部的一个MαCSs,雷达拼图资料也展现了其观测范围广的优势。赵放等(2012)在雷达拼图资料上研究了3个台风登陆前后的雷达回波和降水结构时空变化,利用单多普勒雷达四维变化同化反演技术,反演了三维风场。多位学者利用雷达拼图资料,对MCSs进行了不同的分类研究(Parker et al, 2000; Rigo et al, 2004; 2007; Schumacher et al, 2005)。Gallus等根据雷达回波形态的差异将对流系统分为8类,统计各形态系统与龙卷、冰雹、强降水和大风关系发现,各类线性系统与大风相关性明显好于孤立对流单体、对流云团和非线性系统,弓形回波与大风的相关性最好,甚至明显高于线性对流系统。在这些分类研究基础上,我国长江中下游地区梅雨期线状中尺度对流系统分类研究也得到开展,将长江中下游地区的线状MCSs分为8类分别统计了发生数量、持续时间和各占百分比,发现线状MCSs占所有MCSs比例为52.9%,统计得到镶嵌线状中尺度对流系统(EL)和长带层状降水中尺度对流系统(LL)两种新的分类(王晓芳等,2012)。同期出现了基于雷达资料的MCSs的自动识别跟踪方法研究(Lakshmanan et al, 2003; 王改利等,2007; 杨吉等,2012)。
发展性能良好的MCSs自动识别跟踪方法不仅有利于监测、预警和预报,对研究MCSs活动规律至关重要,能够得到准确和客观的MCSs相关参数,同时大量减少人力物力的消耗。利用雷达资料进行的临近预报,主要是以雷暴识别、跟踪、分析和预报算法(TITAN)与风暴单体识别和跟踪算法(SCIT)为代表的质心跟踪法(王芬等,2010;钟敏等,2012),该类方法适用于γ中尺度的系统。另一类利用相关法跟踪雷达回波(TREC)虽然能够得到较好的雷达回波移动矢量,但该方法对云团的矩形网格划分物理意义不够明确(胡胜等,2010)。因此,新的识别跟踪方法还在被提出。王改利等(2007)使用层级聚类法识别β中尺度对流系统基础上,以云团为区域划分,使用TREC方法计算相邻时刻所有云团的匹配,得到极大值相关系数R的匹配,认为它们是同一个云团。杨吉等(2012)利用Davis等开发的模式评估工具发展了具有明确物理意义的MCSs识别算法,该方法对各种形态的MCSs均有较好的识别效果,能够提取MCSs面积、百分比强度、拟合椭圆长短轴及方向和质心等参数;并且能够实现跟踪与预报,跟踪方法首先设定一个较宽的阈值实现相邻时刻MCSs匹配,然后根据重心距离、面积比和移动方向等参数排除错误匹配来实现跟踪,该方法虽然考虑了分裂与合并,能够实现跟踪与预报,但是由于MCSs内部常发生对流云生消以及分裂与合并导致质心“跳变”,使得跟踪“丢失”现象时有发生,连续时刻移动向量的方向和移动距离起伏不定,导致预报误差较大。本文主要目的是在杨吉等(2012)发展的MCSs识别方法基础上发展一个适用于MCSs的跟踪与预报方法,提高跟踪和预报效果。
1 资料选取原始雷达资料由我国气象部门的新一代天气雷达网提供。使用中国气象科学研究院灾害天气国家重点实验室开发的多普勒天气雷达三维数字组网系统把原始雷达资料转化成雷达拼图资料。该系统首先将不同型号、不同波段雷达的体扫数据转换为统一格式,对统一格式的数据进行质量控制,再采用径向与方位上的最近邻居法和垂直线性内插法将单站雷达数据从极坐标系转换到经纬度和垂直高度坐标系,然后采用指数权重的算法将各单站的格点数据拼到一个大范围的经纬度和垂直高度坐标系中。MCSs识别法使用水平分辨率为0.01°×0.01°的组合反射率因子,时间分辨率为6 min。
选取4次强天气过程,检验、分析算法在不同天气过程中的表现。4次天气过程分别为:2009年6月3-4日,一次强飑线天气过程袭击了我国的黄淮地区,飑线呈“厂”字型,此次天气影响范围大,使用了郑州、商丘、濮阳、三门峡、驻马店、徐州和合肥7部雷达站的基数据进行组网。2011年6月23日,一次MCSs袭击了北京及周边地区,强降水造成城市多处被淹没,两人死亡,此次使用了北京S、天津和承德雷达站基数据进行组网。2011年8月9日,强降水过程袭击北京,造成多个路段积水,航班延误,此次过程使用北京S、天津和承德雷达站基数据进行组网。2012年5月16日,一次线状MCSs横扫苏北,造成冰雹大风和强降水天气,此次使用盐城、连云港、徐州和南京雷达站基数据进行组网。
2 方法 2.1 MCSs识别跟踪方法介绍MCSs识别方法与杨吉等(2012)提出的方法一致,方法介绍如下。根据Houze(1982;1989)提出,中尺度对流系统是指由很多对流云及它们之间连接的层云降水一起组成并以线性或者其他形式存在,以及Geerts (1998)在雷达拼图资料上对MCSs的定义:一个连续的层云降水区域(反射率因子超过20 dBz)长轴至少100 km,存在4 h以上,生命期内至少有2 h的最大反射率因子超过40 dBz,我们采用的方法首先对对流云进行识别(35 dBz),再识别层云(15 dBz),把由层云连接的对流云组织成一个系统,这样的系统如果满足长轴至少100 km,且存在4 h以上,则为是MCSs。具体方法如下:
首先,由雷达拼图资料得到组合反射率因子。然后,进行一个卷积过程,使资料变得光滑,有利于识别成块的回波。卷积过程使用的卷积函数为
| $ C\left({x, y} \right) = \sum {\varphi \left({u, v} \right)f\left({x - u} \right)\left({y - v} \right)} $ | (1) |
式中,f是雷达拼图资料场,φ是滤波函数。变量(x, y)和(u, v)是格点坐标。滤波函数φ是一个简单的由高度H和影响半径R决定的圆形滤波,即
| $ \begin{array}{l} \varphi \left({x, y} \right) = H, \;\;\;\;{\rm{if}}\left({{x^2} + {y^2} \le {R^2}} \right)\\ \varphi \left({x, y} \right) = 0, \;\;\;\;\;{\rm{if}}\left({{x^2} + {y^2} > {R^2}} \right) \end{array} $ | (2) |
参数R和H不相互独立,其关系如下:
| $ \pi {R^2}H = 1 $ | (3) |
卷积过程中影响半径R是唯一可改变的参数。一旦R被选定,H由式(2) 决定。该方法中采用的是4个格距。
得到卷积场后,让场中每一点与第一阈值对比,大于等于第一阈值在该点赋值1,小于则赋值0,识别出对流云,得到对流云场。再使用第二阈值识别出更大范围的层云,得到层云场。把落在同一个层云范围内的对流云归为一个系统,这样就形成了包含大范围层云和多个风暴单体的系统。这样的系统满足长轴大于100 km,且生命期超过4 h,则被认为是中尺度对流系统。同时,相关参数被记录。
原跟踪方法如下:根据连续两个时次识别到的系统之间重心位置的距离实现初次匹配。计算前后时刻实现初次匹配系统的面积比,认为小于面积匹配阈值的不是同一个系统。计算实现初次匹配的单个系统重心距离与其他几个重心距离平均值比值,认为大于重心比阈值的匹配是错误的。以及移动方向,出现交叉移动的匹配,也认为是错误的。排除错误匹配后,剩余的匹配被认为是最终跟踪结果。最后用最小二乘法拟合从MCSs目前直到前1 h位置得到运动向量,然后线性外推预报位置。
2.2 新跟踪方法介绍该方法基于一个假设条件:连续时刻MCSs的雷达回波生消量对自身回波总量来说是较小的,对MCSs的移动矢量不产生大的影响。
首先采用TREC得到每一个矩形网格的移动矢量。TREC方法简单介绍如下:
将整个回波区域划分为若干个20 km×20 km的矩形网格。将前一时刻雷达回波中的某一个矩形网格任意移动一个距离Δr (Δr<搜索半径Range),根据前后两个时刻矩形网格内的雷达回波计算出交叉相关系数Ri。不同的移动距离,得到不同的相关系数值,具有最大相关系数Ri的移动矢量被认为是正确的回波移动,即TREC矢量。依次对每一个矩形网格进行如上的步骤,得到所有矩形网格的移动矢量。交叉相关系数Ri计算公式如下:
| $ {R_i} = \frac{{\sum {{Z_1}\left(i \right){Z_2}\left(i \right) - {n^{ - 1}}\sum {{Z_1}\left(i \right)\sum {{Z_2}\left(i \right)} } } }}{{{{\left[ {\left({\sum {Z_1^2\left(i \right) - n\overline {Z_1^2} } } \right)\left({\sum {Z_2^2\left(i \right) - n\overline {Z_2^2} } } \right)} \right]}^{1/2}}}} $ | (4) |
式中,Z1和Z2分别为前一时刻和后一时刻的反射率因子。n为矩阵的数据点数。
| $ {\rm{Range}} = {V_{\max }} \times \Delta t $ | (5) |
式中,Vmax为雷达回波移动的最大期望速度(文中采用60 km·h-1),Δt为时间间隔。
然后对TREC矢量进行一个简单的质量控制,确保相邻矩形网格的TREC矢量具有较好的连续性,消除零矢量。检查每一个TREC矢量与周围矢量的平均方向,相差超过20°或为零矢量,则用周围8个矩形网格的平均矢量来替代这个TREC矢量。
下一步得到每一个MCSs的移动矢量。通过以下公式计算得到:
| $ {\mathit{\boldsymbol{V}}_x} = {n^{ - 1}}\sum {{n_1}} \times {\mathit{\boldsymbol{v}}_{1x}} $ | (6) |
| $ {\mathit{\boldsymbol{V}}_y} = {n^{ - 1}}\sum {{n_1}} \times {\mathit{\boldsymbol{v}}_{1y}} $ | (7) |
式(6) 和(7) 中,Vx和Vy是得到的MCSs移动矢量,n1表示MCSs回波点落在矩形网格1内的总数,v1x和v1y表示矩形网格1的TREC矢量,n为该MCSs的回波点数总量。
用得到的MCSs移动矢量外推该MCSs雷达回波,计算下一时刻的重叠面积率
| $ {A_O} = \frac{{{A_{ij}}}}{{\min \left[ {{A_i}\left(t \right), {A_j}\left({t + 1} \right)} \right]}} $ | (8) |
式中,Aij为t时刻第i个MCSs与t+1时刻第j个MCSs重叠面积,min[Ai(t), Aj(t+1)]为t时刻第i个MCSs与t+1时刻第j个MCSs面积取最小。AO如果大于阈值(本文取0.6),则认为是同一个MCSs。合并与分裂情况下,计算方法同上。MCSs在t+1时刻发生分裂,分裂后的匹配中,具有最大面积的MCSs被赋予t时刻匹配MCSs的编号,其他分裂的MCSs标记为分裂,赋予新的编号。MCSs在t+1时刻发生合并,t时刻与之匹配的MCSs中,具有最大面积的编号赋给t+1时刻匹配MCSs。
采用线性最小二乘法拟合MCSs目前到前1 h移动矢量,进行线性外推预报。初次探测到的MCSs采用已存在MCSs的平均移动,如果没有平均移动则由用户直接输入运动矢量。
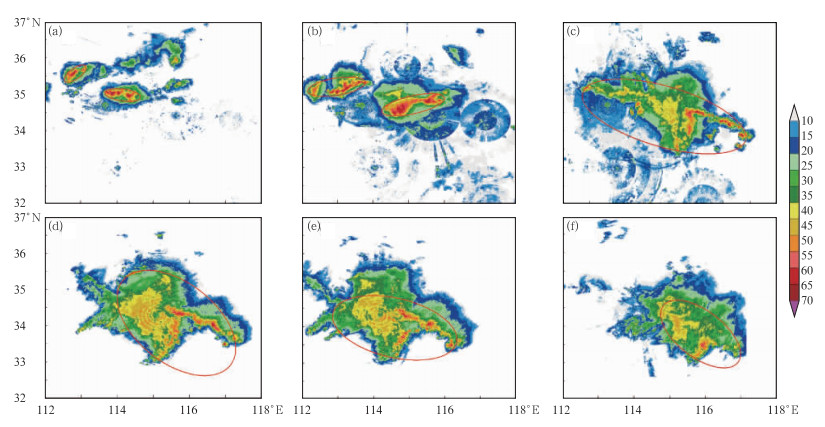
3 结果与分析 3.1 MCSs跟踪分析图 1为新方法处理2009年6月3日黄淮飑线资料后输出跟踪路径,跟踪起点为时刻10:30(UTC,下同),连续跟踪84个时次至18:54,可以看出新方法跟踪效果较好。图 2为2009年6月3日黄淮飑线多个时次识别结果图,图 2a和2b中的两个系统在12:54发生合并,对应在图 1中(34.6°N、115°E)附近矩形内出现一次质心向西北方向的偏移,从该处可以看出,算法在系统合并情况仍然能够实现正确追踪。而从其他3个个例分析来看,算法在系统合并和分裂情况下均能实现追踪,效果较好。18:54后,即图 1中系统中心移速(119.05°,33.65°)点之后的路径不连续,代表了两次跟踪丢失,在处理其他3个天气过程资料中发现,跟踪丢失都发生在系统快速消亡时期,由于回波的快速变化,导致提取速度不稳定(图 3),其他时段跟踪效果较好。图 1中质心总体向东南方向前进,过程中有南北或东西向的波动,由雷达回波的生消和系统发生合并与分裂所致。由此可见,依靠质心得到的系统移动速度必然受到质心偏移的影响(图 3)。分析原方法处理其他3次天气过程资料结果,跟踪丢失现象一般发生在系统合并与分裂时期,而系统的合并与分裂是MCSs天气过程中时常发生的情况。

|
图 1 MCSs跟踪路径 Fig. 1 The tracking path of MCSs |
|
图 2 2009年6月3日黄淮中尺度对流系统识别结果 (a) 10:30, (b) 12:00, (c) 15:00, (d) 16:00, (e) 17:00, (f) 18:30 Fig. 2 MCSs identification in Huanghuai respectively at (a) 10:30, (b) 12:00, (c) 15:00, (d) 16:00, (e) 17:00, and (f) 18:30 UTC 3 June 2009 |
|
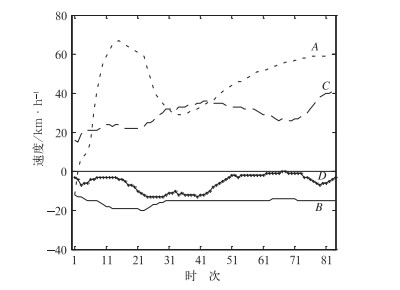
图 3 两种方法提取速 (A和D分别代表原方法得到X方向和Y方向速度,B和C分别代表新方法得到X方向和Y方向速度) Fig. 3 The speed of MCSs extracted by two algorithms (A and D represent velocities extracted by old algorithm in X and Y directions, respectively; B and C represent velocities extracted by new algorithm in X and Y directions, respectively) |
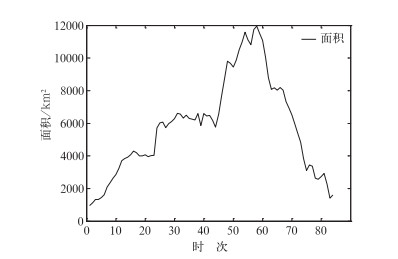
图 3是原方法和新方法提取到2009年6月3日黄淮飑线的移动速度随时间变化。图 3中,横轴表示时次,每个时次时间间隔6 min,纵轴代表速度,单位是km·h-1,A和D分别代表原方法得到X方向速度和Y方向速度,B和C分别代表新方法得到X方向速度和Y方向速度。以东西朝向为X轴,向东为正;以南北朝向为Y轴,向北为正。图 4是MCSs识别算法提取到对应图 3系统的面积随时间变化图,图 3和图 4不包含跟踪丢失时段数据。从图 3来看,A经历了一个速度正向的快速增长,然后下降,再缓慢上升的阶段,而B代表的速度从整体看相对稳定,速度基本保持在20~40 km·h-1,前期速度在20 km·h-1附近,中期速度稍有增加,后期经历小幅度下降后上升。而C和D代表的速度相差不大,保持了相对平稳的走势。下文主要讨论X方向速度,即代表两种方法提取的速度A和B。结合雷达回波实况分析,10:30图 2a中(35°N、114°E)附近系统被算法第一次识别,其后处于快速发展阶段,西侧回波发展迅速,强度较强,东侧回波发展相对较慢,强度较弱,图 4中对应时次系统面积增加,系统向东偏南方向移动,由于回波发展导致质心向西偏移,代表原方法的X方向速度A为负或偏小,不能代表系统的移动速度,代表新方法的X方向速度B则较为合理,并没有受到回波向西发展的影响。第七时次以后,西侧回波开始消亡,东侧不断生成新的对流单体,质心向东移动,从实况上分析来看,系统移动速度并无明显的增加,图 2b中该系统位于(34.8°N、115°E)附近,速度A呈现快速上升的趋势,最高达到66 km·h-1,速度B则基本稳定,稍有正向增加。图 1中矩形框内质心向西北偏移之前,系统移过了近1.5°经度,纬向仅移过约0.5°,大致印证了两种方法提取系统移动速度(图 3)的合理性。到第二十四个时次系统与西侧的一个对流系统发生合并,图 4中对应时次系统面积出现了约2000 km2的“跃升”,图 1中出现了矩形内的质心向西北偏移,此时A速度明显受到系统合并的影响,开始快速下降,其下降的速度不能代表真实情况,对应时间段B速度没有受到系统合并影响,速度值甚至小幅度上升。由于A速度由系统质心位置拟合前1 h相关信息得到,系统合并后质心位置相对合并前都是偏向西,故速度A连续下降1 h,到第三十五时次后,合并带来的速度减小影响过去,速度再次正向回升,其回升的速度趋势同样不能表示系统开始加速移动。到第四十五时次附近时,东侧回波开始快速发展,西侧缓慢减弱,图 2c东侧可见一条西北东南朝向的强回波带,图 4中对应时次面积迅速增加,速度A受到东侧回波发展的影响,继续保持上升的趋势,速度B则无明显影响,出现小幅度下降。在第五十七时次附近,系统回波面积发展到最大(图 4),此后系统进入消亡期,西侧回波明显弱于东侧,西侧回波消亡相对较快,图 2d和2e中西侧回波带已基本消亡,速度A仍然呈上升趋势。速度B后期出现一个下降后上升,这可能是由于回波过快消亡,算法提取速度不稳定造成。系统主要运动为东西向,南北向速度相对较慢,代表原方法Y方向速度B总体较为稳定,速度的小幅度波动也是由系统合并和回波生消造成,与速度A情况一致。代表新方法Y方向速度D变化幅度较小,总体较为稳定。
|
图 4 MCSs面积随时间变化 Fig. 4 Area of MCSs changed with time |
多位学者以往研究表明,MCSs的运动包含了系统的移动与传播,传播指风暴单体的不断消失与生成的新陈代谢过程。通过这次飑线过程来看,原方法能够得到系统的移动速度,在无分裂与合并情况下,能够得到系统移动和传播的合成矢量,但在系统初生期、合并与分裂情况下,得到速度出现较大波动,不能较好代表系统移动情况。新方法能够得到系统的移动速度,速度较为稳定,不受系统合并和分裂的明显影响,具有相对较好代表性,但不能得到系统的传播速度。分析本文中其他3次天气过程,得到结论与上文一致(图略)。
3.3 预报误差对比分析对4次强对流天气过程资料进行处理,共识别出468个误差样本。将原方法和新方法得到预报位置与相应质心位置进行比较得到表 1。新方法的6~60 min预报误差都明显小于原方法,误差减小达到20%以上。上文中较大幅度波动的系统移动速度对应了较大预报误差,相对稳定的速度对应了较小误差,具有较好的相互印证关系。
|
|
表 1 中尺度对流系统预报算法不同预报时间的平均预报误差 Table 1 The averaged forecast errors in the MCSs nowcasting for the different lead times |
本文在中尺度对流系统自动识别基础上,提出了新的MCSs跟踪和预报方法。采用新方法和原方法对4次强天气过程资料进行处理,对比分析,得到以下结果。
(1) 新方法能够有效实现跟踪和预报,跟踪和预报效果较好。新方法能够避免因为合并、分裂和回波生消导致跟踪不稳定和提取速度大幅度波动的现象。有效减小预报误差,6~60 min预报误差与原方法相比均减小20%以上。
(2) 新方法虽然能提取较为稳定的系统移动速度,但不能得到系统的传播速度。原方法能得到系统的移动速度和传播速度合成,但提取速度不稳定,容易受到质心偏移的影响,预报误差较大。新方法在系统消亡期提取移动速度不稳定,出现跟踪丢失现象;原方法在系统合并与分裂时易出现跟踪丢失现象。
(3) 从实现有效跟踪和减小预报误差的角度出发,新方法好于原方法,更具有实用价值。
贝耐芳, 赵思雄, 2002. 1998年"二度梅"期间突发强暴雨系统的中尺度分析[J]. 大气科学, 26(4): 526-540. |
方翀, 毛冬艳, 张小雯, 等, 2012. 2012年7月21日北京地区特大暴雨中尺度对流条件和特征初步分析[J]. 气象, 38(10): 1278-1287. DOI:10.7519/j.issn.1000-0526.2012.10.014 |
胡胜, 罗兵, 黄晓梅, 梁巧倩, 等, 2010. 临近预报系统(SWIFT)中风暴产品的设计及应用[J]. 气象, 36(1): 54-58. DOI:10.7519/j.issn.1000-0526.2010.01.008 |
孙虎林, 罗亚丽, 张人禾, 等, 2011. 2009年6月3—4日黄淮地区强飑线成熟阶段特征分析[J]. 大气科学, 35(1): 105-119. |
王改利, 刘黎平, 2007. 暴雨云团的多尺度识别方法及其在临近预报中的应用[J]. 大气科学, 31(3): 400-409. |
王芬, 李腹广, 张辉, 2010. 风暴单体识别与跟踪(SCIT)算法评估[J]. 气象, 36(12): 128-133. DOI:10.7519/j.issn.1000-0526.2010.12.019 |
王婧羽, 崔春光, 王晓芳, 等, 2014. 2012年7月21日北京特大暴雨过程的水汽输送特征[J]. 气象, 40(2): 133-145. DOI:10.7519/j.issn.1000-0526.2014.02.001 |
王晓芳, 崔春光, 2012. 长江中下游地区梅雨期线状中尺度对流系统分析Ⅰ:组织类型特征[J]. 气象学报, 70(5): 909-923. DOI:10.11676/qxxb2012.077 |
杨吉, 刘黎平, 李国平, 等, 2012. 基于雷达回波拼图资料的风暴单体和中尺度对流系统识别、跟踪及预报技术[J]. 气象学报, 70(6): 1347-1355. DOI:10.11676/qxxb2012.113 |
易笑园, 李泽椿, 姚学祥, 等, 2011. 一个固囚状中尺度对流系统的多尺度结构分析[J]. 气象学报, 69(2): 249-262. DOI:10.11676/qxxb2011.021 |
俞小鼎, 2012. 2012年7月21日北京特大暴雨成因分析[J]. 气象, 38(11): 1313-1329. |
俞小鼎, 郑媛媛, 廖玉芳, 等, 2008. 一次伴随强烈龙卷的强降水超级单体风暴研究[J]. 大气科学, 32(3): 508-522. |
张小玲, 陶诗言, 张顺利, 2004. 梅雨锋上的三类暴雨[J]. 大气科学, 28(2): 187-205. |
赵放, 冀春晓, 高守亭, 等, 2012. 浙江沿海登陆台风结构特性的多普勒雷达资料分析[J]. 气象学报, 70(1): 15-29. DOI:10.11676/qxxb2012.002 |
钟敏, 吴翠红, 王珊珊, 等, 2012. CINRAD/SA雷达两种识别跟踪产品的评估分析[J]. 气象, 38(6): 722-727. DOI:10.7519/j.issn.1000-0526.2012.06.010 |
Gallus JR., Nathan A. Snook, Elise V.Johnson.2008: Spring and summer severe weather reports over the midwest as a function of convective mode: a preliminary study. Wea Forecasting, 23, 101-113.
|
Geerts B, 1998. Mesoscale convective systems in the southeast united states during 1994-95: A Survey[J]. Wea Forecasting, 13: 860-869. DOI:10.1175/1520-0434(1998)013<0860:MCSITS>2.0.CO;2 |
Houze R A Jr, 1982. Cloud cluster and large-scale vertical motions in the tropics[J]. J Meteor Soc Japan, 60: 396-409. DOI:10.2151/jmsj1965.60.1_396 |
Houze R A Jr, 1989. Observed structure of mesoscale convective systems and implications for large-scale heating[J]. Quart J Roy Meteor Soc, 115: 425-461. DOI:10.1002/(ISSN)1477-870X |
Lakshmanan V, Rabin V R, DeBrunner V, 2003. Mltiscale Strom Identification and Forecast[J]. J Atmos Res, 4: 367-380. |
Parker M D, Johnson R H, 2000. Organizational modes of midlatitude mesoscale convective systems[J]. Mon Wea Rev, 128: 3413-3436. DOI:10.1175/1520-0493(2001)129<3413:OMOMMC>2.0.CO;2 |
Rigo T, Llasat M C, 2004. A Methodology for the Classification of Convective Structure using Meteorogical Radar: Application to Heavy Rainfall Events on the Mediterranean Coast of the Iberian Peninsula[J]. Natural Hazards and Earth System Sciences, Ed. European Geosciences Union, 4(1): 59-68. DOI:10.5194/nhess-4-59-2004 |
Rigo T, Llasat M C, 2007. Analysis of Mesoscale Convective Systems in Catalonia using meteorological radar for the period 1996-2000[J]. Atmospheric Research, 83: 458-472. DOI:10.1016/j.atmosres.2005.10.016 |
Schumacher R S, Johnson R H, 2005. Organization and Environmental Properties of Extreme-Rain-Producing Mesoscale Convective Systems[J]. Mon Wea Rev, 133: 961-976. DOI:10.1175/MWR2899.1 |
William A, Gallus J R, Nathan A Sn, et al, 2008. Spring and summer severe weather reports over the midwest as a function of convective mode: A preliminary study[J]. Wea Forecasting, 23: 101-113. DOI:10.1175/2007WAF2006120.1 |
 2015, Vol. 41
2015, Vol. 41 
