2. 中国科学院大气物理研究所,北京 100029;
3. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
3. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
登陆台风的强降水及由此引发的洪水、水库崩塌及泥石流等是造成与台风相关的许多重大灾害的直接原因(Chen et al, 2006)。登陆台风对人类生存环境及社会和经济影响巨大,即使科学技术高度发展的今天,人们在这样的庞然大物面前仍然显得束手无策,因此对登陆台风强降水的研究一直是气象工作者研究的热点和难点之一。
针对台风登陆过程,尤其是登陆过程中产生的降水,气象学者开展了大量的研究工作,内容涉及大尺度环流、水汽供应、地形、冷空气及中尺度结构变化等对登陆台风降水强度、分布、维持机理等众多方面(蔡则怡等, 1997;潘志祥等,2001;梁旭东等, 2002;曾智华等,2002;雷小途,2002;钮学新等,2005;Li et al, 2005;程正泉等,2005;2014;李英等,2005;2006;2013;袁子鹏等,2006;冀春晓等, 2007;陈永林等,2009;周玉淑等,2014;沈杭锋等,2014;文永仁等,2014)。由于降水本身所具有的复杂性以及登陆过程中复杂的多尺度相互作用和海陆气相互作用,使得人们对台风登陆过程的理解和认识仍十分欠缺,这也直接影响了台风降水的预报水平,亟待突破。
2009年第8号台风莫拉克(Morakot)8月4日凌晨生成,5日加强为台风,7日23:45在台湾花莲登陆,9日16:20在福建霞浦再次登陆,9日晚上在福建省境内减弱为强热带风暴,10日凌晨减弱为热带风暴,12日02时停止编号。从生成到结束9天时间里给我国多省(市)带来严重创伤,其中台湾受创最严重。台湾地区累计降水量高达2777 mm,创下了近50年来最严重的水灾,并导致严重的泥石流和洪涝灾害,给台湾南部地区带来惨重的创伤,造成超过600人死亡,92人失踪,约47亿美元的损失。关于台风莫拉克已经有很多相关的研究(刘峰等,2011;周立等,2011;张建海等,2011;李波等,2011;许娈等,2013),本文将利用中尺度非静力WRF模式,对此次台风登陆过程展开高分辨率数值模拟,并利用各种观测资料对模拟结果进行验证。在保证模拟与实况较为一致的情况下,利用高分辨率的模拟结果开展“莫拉克”台风的动力结构诊断及其对降水影响的分析。
1 高分辨率数值模拟及检验本文选取1°×1°分辨率NCEP/NCAR再分析资料(间隔6 h)形成初始场,利用WRF模式模拟“莫拉克”台风的登陆过程。模式积分时间从2009年8月6日12时(UTC)开始,到8月9日12时结束,共积分72 h。模拟采用水平分辨率分别为18、6和2 km的三重嵌套方案,网格点数分别为103×105(D01), 148×145(D02), 205×205(D03),模式积分区域中心为(25°N、120°E),垂直方向上分为28个不等距的σ层,时间积分步长30 s,模式输出资料间隔为3 h。为了更好地模拟出“莫拉克”的结构,本文使用了一个Bogus初始化方案,首先将初始场中的TC涡旋滤去,然后再生成一个动力和热力相平衡的TC涡旋,将这个TC涡旋植入已经滤除的TC涡旋的初始场中形成新的初始场。本次模拟选用质量坐标(Eulerian mass coordinate), Runge-Kutta 3阶时间积分方案, 模式微物理过程采用Ferrier方案和Kain-Fritsch积云对流参数化方案,同时采用MRF边界层方案,Dudhia短波辐射和RRTM长波辐射方案。
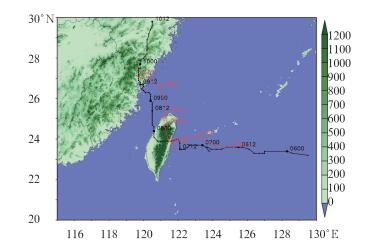
图 1给出了模拟(红线)与观测(黑线)的“莫拉克”台风路径。由图可见,模式对“莫拉克”台风路径的模拟比较成功。“莫拉克”开始时向西移动,逐渐靠近台湾后突然向北转折,并在8月7日12时首先登陆台湾,登陆后以较慢的速度穿越台湾岛,随后沿西北向移动,并在福建省再次登陆。
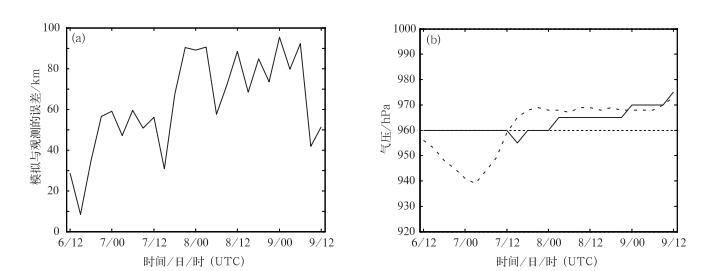
从图 2a可以看出,从模拟的开始时刻一直到8月9日12时,模拟与观测的台风路径及中心位置都比较吻合,模拟的中心位置与实际观测的误差在100 km之内,属于可接受的误差范围。
|
图 1 “莫拉克”台风实况路径(黑线)与模拟路径(红线) Fig. 1 Observed path (black line) and simulated path (red line) of Typhoon Morakot |
|
图 2 2009年8月6日12时至9日12时(a)模拟的“莫拉克”台风的中心位置与实际观测的误差;(b)“莫拉克”台风实况中心海平面气压(实线)与模拟中心海平面气压(虚线) Fig. 2 (a) Deviation between simulated and observed Typhoon Morakot centers during 12:00 UTC 6 to 12:00 UTC 9 August 2009; (b) observed center sea level pressure (solid line) and simulated center sea level pressure (dotted line) of Morakot |
模拟与观测的“莫拉克”台风中心气压变化如图 2b所示。由图可见,模拟与观测的台风中心气压变化趋势比较一致,模式较好地再现了“莫拉克”台风在登陆台湾(8月7日12时)之后的中心海平面气压的变化过程。模拟的台风在8月7日12时之前较实况偏弱,其原因可能是初始场中的人造Bogus的TC涡旋在模式中有一个自适应的过程,在模式开始的前6 h内,TC涡旋逐渐加强,之后又逐渐减弱,8月7日12时之后与实况的中心海平面气压基本一致。总体来看,模式还是比较好地再现了“莫拉克”台风发展演变过程中的路径和强度变化特征。
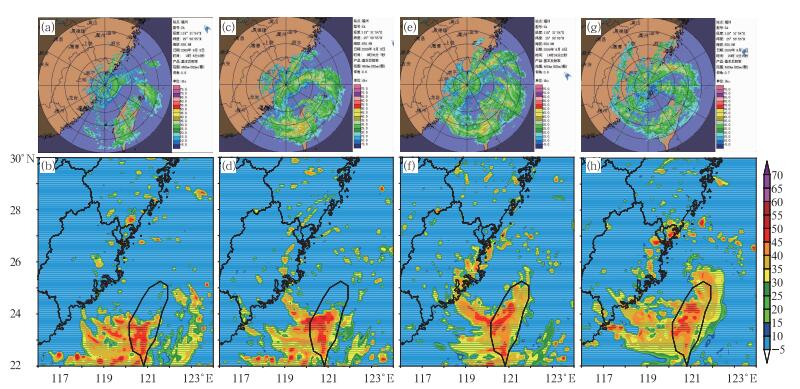
图 3给出了2009年8月7—8日“莫拉克”台风登陆期间模拟雷达回波与实况的对比情况。总的来看,模拟的雷达回波分布与实况分布形式较为一致,台风眼区、眼壁以及外围螺旋雨带回波都有较好的对应,这为研究台风登陆过程中台风结构、强度乃至风雨的演变提供了基础。8月7日18时,模拟的台湾岛中南部的雷达回波分布和强度与实况都较为一致,实况中浙江省与福建省交界处的雷达回波也有较好体现,但是福建省东北部和台湾岛北部的雷达回波模拟的范围和强度都较实况偏小。8月8日00时,模拟的台湾岛中南部的雷达回波分布与强度与实况都较为一致,浙江省与福建省交界处以及福建省东北部的雷达回波较实况偏弱,台湾岛北部的雷达回波没有模拟出来。8月8日06时,台湾岛中西部的强雷达回波模拟的较为成功,台南地区的雷达回波模拟的略偏强,福建省东部沿海地区的雷达回波也模拟较好。8月8日12时,模拟效果与06时相当,但福建省中西部有一条狭长的雷达回波没有模拟出来。
|
图 3 模拟的“莫拉克”台风的雷达回波(b, d, f, h)与实况(a, c, e, g)的对比 (a, b) 7 日 18 时, (c, d) 8 日 00 时, (e, f) 8 日 06 时, (g, h) 8 日 12 时 Fig. 3 Comparison between simulated (b, d, f, h) and observed (a, c, e, g) radar echoes of Morakot (a, b) 18:00 UTC 7, (c, d) 00:00 UTC 8, (e, f) 06:00 UTC 8, (g, h) 12:00 BT 8 August 2009 |
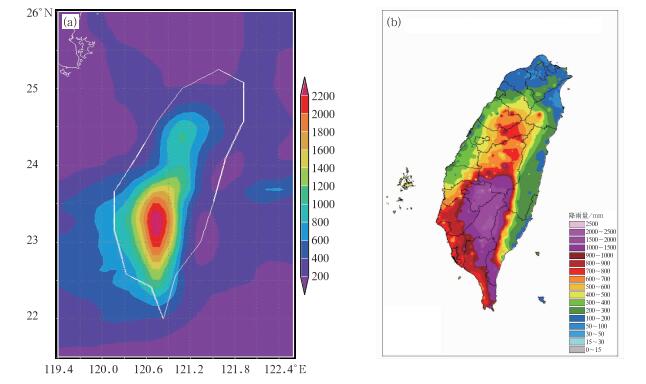
图 4给出了模拟与实况地面72 h累积降水分布的对比。从8月6日12时到9日12时的地面累积72 h降水分布可以看出,模式较好地模拟出了位于台湾岛中南部的降水大值区,无论从降水区的分布还是从降水量的强度来看,本次模拟的“莫拉克”台风,在台湾岛地区的3天过程降水量都比较成功。
|
图 4 2009年8月6日12时至9日12时模拟的“莫拉克”台风的地面72 h累积降水分布 (a)与实况(b)的对比 Fig. 4 Comparison between simulated 72 h surface accumulated precipitation distribution (a) and observation (b) of Typhoon Morakot during 12:00 UTC 6 to 12:00 UTC 9 August 2009 |
通过以上从路径、强度、雷达回波以及72 h降水分布等几方面的对比分析可以看出,此次“莫拉克”台风的发展、演变以及登陆过程的模拟还是比较成功的,模式输出的高时空分辨率资料,为深入细致地研究“莫拉克”台风发展及登陆过程提供了很好的资料准备。
2 广义波作用密度的诊断分析波流相互作用是大气科学中一个重要研究内容,很多重要的天气现象都可以利用波流相互作用理论进行解释,例如:赤道平流层东西风准两年振荡(Lindzen et al, 1968),平流层爆发性增温(Matsuno, 1970)和高空急流加速增强(Shepherd, 1990; Pfeffer, 1992)等。波流相互作用理论除了较多地用于大尺度行星波传播的研究外,还可以用于与暴雨过程密切相关的扰动动力学分析。Gao等(2009)采用位涡定理,考虑水汽效应,建立了适用于暴雨中尺度扰动系统研究的水汽波作用方程和热力波作用方程。Ran等(2010)利用扰动热力切变平流参数(本质上是一种波作用密度)对登陆台风Wilpa雨带形成的动力学过程进行了研究。本文将在以往研究的基础上,对本次登陆台风雨带内中尺度扰动的波活动特征进行诊断分析,并讨论波流相互作用对相关扰动发展演变的影响。
局地直角坐标系中广义波作用密度M及相应的基本量M0的倾向方程如下(详见附录及周冠博等,2013):
| $ \begin{align} & \frac{\partial M}{\partial t}=\nabla \cdot {\mathit{\boldsymbol{{F}}}_{1}}+\nabla \cdot {\mathit{\boldsymbol{{F}}}_{2}}+\nabla \cdot {\mathit{\boldsymbol{{F}}}_{e}}+ \\ &\ \ \ \ \ \ \ \ \ \nabla \cdot \left[ {{S}_{\theta _{e}^{*}}}\nabla \times \left(\mathit{\boldsymbol{k}}\times {\mathit{\boldsymbol{{v}}}_{he}} \right) \right] \\ \end{align} $ | (1) |
| $ \frac{\partial {{M}_{0}}}{\partial t}=\nabla \cdot {{\mathit{\boldsymbol{F}}}_{01}}+\nabla \cdot {\mathit{\boldsymbol{{F}}}_{02}}+\nabla \cdot {\mathit{\boldsymbol{{F}}}_{03}}-\nabla \cdot {\mathit{\boldsymbol{{F}}}_{e}} $ | (2) |
式中,
| $ \begin{align} & M=-\left(\frac{\partial {{u}_{e}}}{\partial z}\frac{\partial \theta _{e}^{*}}{\partial x}+\frac{\partial {{u}_{e}}}{\partial z}\frac{\partial \theta _{e}^{*}}{\partial y} \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \left(\frac{\partial {{u}_{e}}}{\partial x}+\frac{\partial {{v}_{e}}}{\partial y} \right)\frac{\partial \theta _{e}^{*}}{\partial z} \\ \end{align} $ | (3) |
为广义波作用密度,作为二阶扰动量,其本质上代表了一种扰动能量。其基本态可以写为:
| $ \begin{align} & {{M}_{0}}=-\left(\frac{\partial {{u}_{0}}}{\partial z}\frac{\partial \theta _{0}^{*}}{\partial x}+\frac{\partial {{v}_{0}}}{\partial z}\frac{\partial \theta _{0}^{*}}{\partial y} \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \left(\frac{\partial {{u}_{0}}}{\partial x}+\frac{\partial {{v}_{0}}}{\partial y} \right)\frac{\partial \theta _{0}^{*}}{\partial z} \\ \end{align} $ | (4) |
考虑到实际大气往往既不是绝对干的,也不是处处饱和的,而是处于一种非均匀饱和状态,人们通常利用广义位温(Gao et al, 2004)来描述这种热力学状态,即:
| $ {{\theta }^{*}}=\theta \exp \left[ \frac{{{L}_{v}}{{q}_{vs}}}{{{c}_{p}}{{T}_{c}}}{{\left(\frac{{{q}_{v}}}{{{q}_{vs}}} \right)}^{k}} \right] $ |
式中,qvs为饱和水汽比湿,Tc为抬升凝结高度处的温度,k为经验常数。利用热力学方程,广义位温的倾向方程可以写为:
| $ \frac{\text{d}{{\theta }^{*}}}{\text{d}t}={{S}_{{{\theta }^{*}}}}$ |
式中,
方程(1) 左端是M的局地变化项,右端为波作用通量散度。由于M表征的是一种扰动能量,因此波作用方程(1) 在一定程度上可以描述这种扰动能量的发展演变以及基本态对扰动的强迫作用。
方程(1) 右端第一项中的F1代表扰动非地转风与扰动广义位温空间梯度的综合作用;该项还可以写为
| ${\mathit{\boldsymbol{{F}}}_{eD}}=\left(\begin{align} & {{w}_{e}}\frac{\partial {{u}_{e}}}{\partial z}\frac{\partial \theta _{0}^{*}}{\partial z} \\ & {{w}_{e}}\frac{\partial {{v}_{e}}}{\partial z}\frac{\partial \theta _{0}^{*}}{\partial z} \\ & -{{u}_{e}}\frac{\partial {{u}_{e}}}{\partial x}\frac{\partial \theta _{0}^{*}}{\partial x}-{{v}_{e}}\frac{\partial {{v}_{e}}}{\partial y}\frac{\partial \theta _{0}^{*}}{\partial y} \\ \end{align} \right) $ |
代表二阶扰动的动量平流输送与广义位温基本态梯度的耦合作用;
| $ {\mathit{\boldsymbol{{F}}}_{eT}}=\left(\begin{align} & -{{w}_{e}}\frac{\partial \theta _{e}^{*}}{\partial z}\frac{\partial {{u}_{0}}}{\partial z} \\ & -{{w}_{e}}\frac{\partial \theta _{e}^{*}}{\partial z}\frac{\partial {{v}_{0}}}{\partial z} \\ & {{u}_{e}}\frac{\partial \theta _{e}^{*}}{\partial x}\frac{\partial {{u}_{0}}}{\partial x}+{{v}_{e}}\frac{\partial \theta _{e}^{*}}{\partial y}\frac{\partial {{v}_{0}}}{\partial y} \\ \end{align} \right)$ |
代表二阶扰动的热量平流输送与基本气流切变的耦合作用,因此
方程(2) 左端是M0的局地变化项,右端的前两项是基本态的通量散度项,右端后两项为二阶扰动的通量散度项,代表扰动对基本态的反馈作用。方程(2) 右端第一项代表非地转风基本态引起的非地转风位涡基本态对M0局地变化的影响,这是因为该项还可以写为
台风内的中尺度波动是影响台风结构、台风移动和强度及台风降水分布的重要因素(徐祥德等,2004;康建伟等,2007;李英等,2007),建立在非均匀饱和湿空气动力框架下的广义波作用密度能够追踪与降水有关的波动信号,从而可能指示台风内的降水分布。为此,本文利用上述波流相互作用理论对登陆台风莫拉克2009年8月7日00 UTC至11日00 UTC的暴雨过程进行诊断分析,利用高分辨率的数值模拟资料分别对广义波作用密度M和波流相互作用项
图 5为2009年8月8日00—18时四个时次的观测6 h累积地面降水(阴影区)和M绝对值垂直积分的水平分布。由图 5可见,波作用密度M的高值区基本覆盖着观测降水区,M在强降水区表现为异常强信号,而在非降水区表现为弱信号;另外,某些局地弱降水区也伴随有较弱的M正值区;这些表明降水区上空存在明显的波作用密度所表征的综合扰动,该扰动与降水系统的发展演变密切相关。
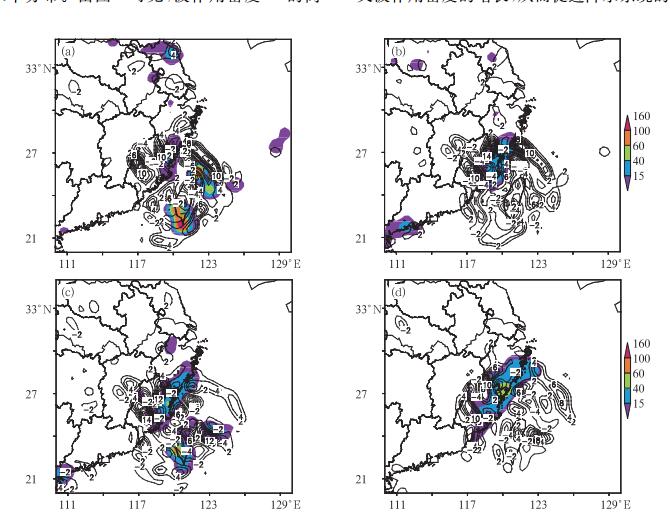
|
图 5 2009年8月8日00时(a)、06时(b)、12时(c)和18时(d)四个时次M的垂直积分平均分布(单位:105 kg·m-1·s-1) (阴影区为观测6 h累积地面降水,单位:mm) Fig. 5 Average distribution of vertical integration of M at 00:00 UTC (a), 06:00 UTC (b), 12:00 UTC (c) and 18:00 UTC (d) 8 August 2009 (unit: 105 kg·m-1·s-1) (Shadow is the observed 6 h accumulated surface precipitation, unit: mm) |
在垂直分布上(图 6),波作用密度的正高值区与观测的6 h累积强降水区也基本保持一致,这进一步说明在暴雨过程中,雨区上空的对流层中下层存在显著的波作用密度所表征的波扰动,该扰动与暴雨的发生发展密切相关。为了分析影响波作用密度发展演变的主要因素,本文对方程(1) 和(2) 中的交换项
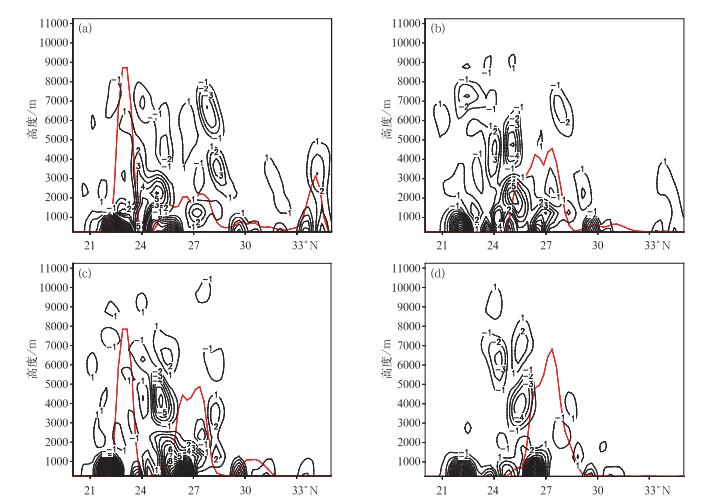
|
图 6 2009年8月8日00时(a)、06时(b)、12时(c)和18时(d)四个时次的M沿121°E的剖面分布(单位:105 kg·m-1·s-1) (粗实线为观测6 h累积地面降水沿121°E的剖面分布,单位:mm) Fig. 6 Section distribution of M along 121°E at 00:00 UTC (a), 06:00 UTC (b), 12:00 UTC (c) and 18:00 UTC (d) 8 August 2009 (unit: 105 kg·m-1·s-1 (Thick solid line is the section distribution of observed 6 h accumulated surface precipitation along 121°E, unit: mm) |
从图 7可以看到,
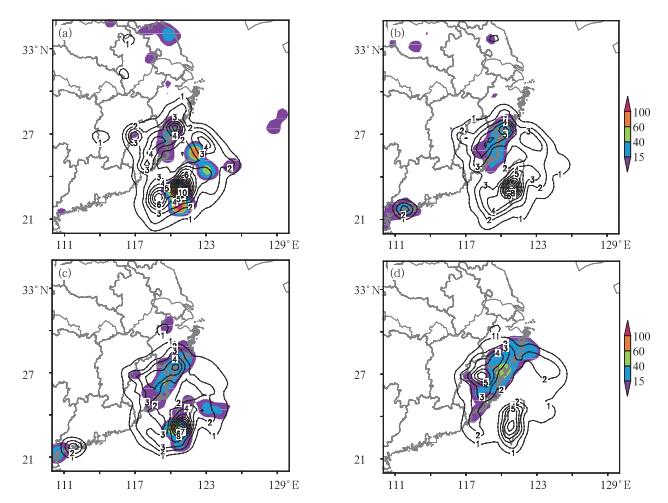
|
图 7 同图 5,但为
|
垂直分布上(图 8),
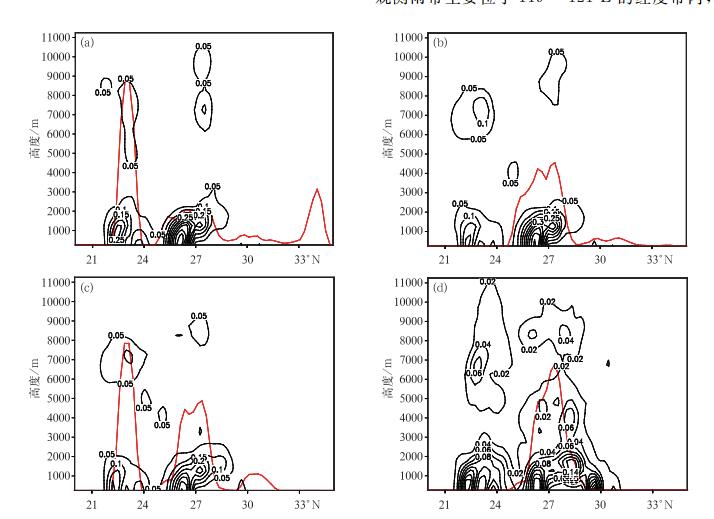
|
图 8 同图 6,但为 |
图 9给出了不同垂直剖面上观测降水与波流相互作用项时间演变趋势。如图 9所示,沿120°E的经向剖面的观测雨带主要位于26°~29°N纬度带内,8月9日06时的降水最强,沿27°N纬向剖面的观测雨带主要位于119°~121°E的经度带内,8月9日00时的降水最强。波流相互作用项
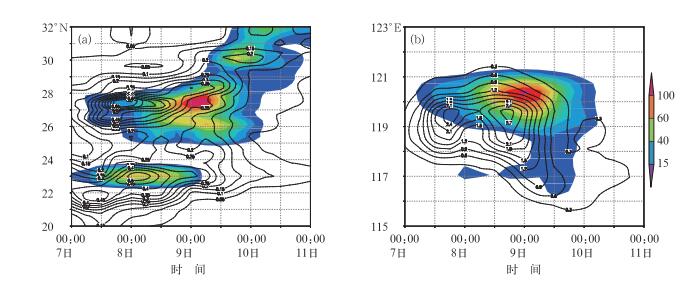
|
图 9 2009年8月7日00时至11日00时 |
以上研究结果表明,广义波作用密度的异常值区始终伴随着观测降水区的发展而起伏变化,两者在水平分布和时间演变趋势上均比较接近。广义波作用密度能够比较准确地刻画降水系统典型的动力场和热力场扰动的水平分布和垂直结构,因而可以有效地表征降水系统的发展和移动。而波流相互作用项的高值区也与降水大值区有较好对应关系,这说明在降水过程中,雨区上空的对流层中低层存在较强的波流相互作用,对降水具有一定指示作用。
3 结论与讨论本文利用非静力中尺度WRF模式对2009年第8号台风莫拉克的发展演变及其登陆过程开展了高分辨率数值模拟,并对模拟结果进行了初步验证。结果表明,模拟较好地再现了“莫拉克”台风的发展演变及其登陆过程。模拟的台风路径与观测路径比较一致,模拟的中心位置与实际观测的误差在100 km之内,属于可接受的误差范围。同时模式也较好地再现了“莫拉克”台风强度演变、主要雷达回波特征以及相应的降水分布特征等。
利用模式输出的高时空分辨率资料,对此次台风登陆过程开展了广义波作用密度(M)的诊断分析。结果表明,在整个研究时段内,M的异常值区始终覆盖在地面雨区之上,两者的空间分布和时间演变趋势比较相似,并且在雨区内M表现为强信号,而在非雨区M表现为弱信号。这表明广义波作用密度能够综合地表征降水系统动力场和热力场扰动的典型结构,利用广义波作用密度可以比较准确地描述“莫拉克”台风登陆前后的发展演变过程,对强降水落区有一定指示意义。
本文主要从高分辨率数值模拟入手,结合波流相互作用理论研究了登陆台风莫拉克强降水过程的特点,而对其相关动热力结构以及云微物理方面的研究还没有涉及。众所周知,降水是宏观动力过程与云微物理过程相结合的产物,要想全面理解和认识登陆台风强降水过程进而提高预报水平,就必须同时关注影响登陆台风强降水的宏观动热力过程以及云微物理过程特征。未来将进一步关注台风莫拉克的热力以及云微物理过程特征等问题,以期加深对登陆台风强降水过程的理解和认识,并进而提高其预报水平。
附录方程(1) 和(2) 右端各项表达式分别为
| $ {\mathit{\boldsymbol{{F}}}_{1}}=\mathit{\boldsymbol{f}}{{v}_{ae}}\times \nabla \theta _{e}^{*} $ | (A1) |
| $ {\mathit{\boldsymbol{F}}_{2 = }}\left( \begin{array}{l} \left[ \begin{array}{l} \left( {{u_0}\frac{{\partial {\theta _e}^*}}{{\partial x}} + {v_0}\frac{{\partial {\theta _e}^*}}{{\partial y}} + {u_e}\frac{{\partial {\theta _0}^*}}{{\partial x}} + {v_e}\frac{{\partial {\theta _0}^*}}{{\partial y}}} \right)\frac{{\partial {u_e}}}{{\partial z}}\\ - \left( {{u_0}\frac{{\partial {u_e}^*}}{{\partial x}} + {v_0}\frac{{\partial {u_e}^*}}{{\partial y}} + {u_e}\frac{{\partial {\theta _0}^*}}{{\partial x}} + {v_e}\frac{{\partial {u_0}^*}}{{\partial y}}} \right)\frac{{\partial {\theta _e}^*}}{{\partial z}} \end{array} \right]\\ \left[ \begin{array}{l} \left( {{u_0}\frac{{\partial {\theta _e}^*}}{{\partial x}} + {v_0}\frac{{\partial {\theta _e}^*}}{{\partial y}} + {u_e}\frac{{\partial {\theta _0}^*}}{{\partial x}} + {v_e}\frac{{\partial {\theta _0}^*}}{{\partial y}}} \right)\frac{{\partial {v_e}}}{{\partial z}}\\ - \left( {{u_0}\frac{{\partial {v_e}^*}}{{\partial x}} + {v_0}\frac{{\partial {v_e}^*}}{{\partial y}} + {u_e}\frac{{\partial {v_0}^*}}{{\partial x}} + {v_e}\frac{{\partial {v_0}^*}}{{\partial y}}} \right)\frac{{\partial {\theta _e}^*}}{{\partial z}} \end{array} \right]\\ \left( {\left[ \begin{array}{l} \left( {{v_0}\frac{{\partial {u_e}}}{{\partial y}} + {w_0}\frac{{\partial {u_e}}}{{\partial z}} + {v_e}\frac{{\partial {u_0}}}{{\partial y}} + {w_e}\frac{{\partial {u_0}}}{{\partial z}}} \right)\frac{{\partial {\theta _e}^*}}{{\partial z}}\\ + \left( {{u_0}\frac{{\partial {v_e}}}{{\partial x}} + {w_0}\frac{{\partial {v_e}}}{{\partial z}} + {u_e}\frac{{\partial {v_0}^*}}{{\partial x}} + {w_e}\frac{{\partial {v_0}}}{{\partial z}}} \right)\frac{{\partial {\theta _e}^*}}{{\partial y}} - \\ \left( {{v_0}\frac{{\partial {\theta _e}^*}}{{\partial y}} + {w_0}\frac{{\partial {\theta _e}^*}}{{\partial z}} + {v_e}\frac{{\partial {\theta _0}^*}}{{\partial y}} + {w_e}\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right)\frac{{\partial {u_e}}}{{\partial z}}\\ - \left( {{u_0}\frac{{\partial {\theta _e}^ * }}{{\partial x}} + {w_0}\frac{{\partial {\theta _e}^*}}{{\partial z}} + {u_e}\frac{{\partial {\theta _0}^ * }}{{\partial x}} + {w_e}\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right)\frac{{\partial {v_e}}}{{\partial y}} \end{array} \right]} \right) \end{array} \right) $ | (A2) |
| $ {\mathit{\boldsymbol{{F}}}_{e}}={\mathit{\boldsymbol{{F}}}_{eD}}+{\mathit{\boldsymbol{{F}}}_{eT}}$ | (A3) |
| $ {\mathit{\boldsymbol{{F}}}_{eD}}=\left(\begin{align} & {{w}_{e}}\frac{\partial {{u}_{e}}}{\partial z}\frac{\partial {{\theta }_{0}}^{*}}{\partial z} \\ & {{w}_{e}}\frac{\partial {{v}_{e}}}{\partial z}\frac{\partial {{\theta }_{0}}^{*}}{\partial z} \\ & -{{u}_{e}}\frac{\partial {{u}_{e}}}{\partial x}\frac{\partial {{\theta }_{0}}^{*}}{\partial x}-{{v}_{e}}\frac{\partial {{v}_{e}}}{\partial y}\frac{\partial {{\theta }_{0}}^{*}}{\partial y} \\ \end{align} \right)$ | (A4) |
| $ {\mathit{\boldsymbol{{F}}}_{eT}}=\left(\begin{align} & -{{w}_{e}}\frac{\partial {{\theta }_{e}}^{*}}{\partial z}\frac{\partial {{u}_{0}}}{\partial z} \\ & -{{w}_{e}}\frac{\partial {{\theta }_{e}}^{*}}{\partial z}\frac{\partial {{v}_{0}}}{\partial z} \\ & {{u}_{e}}\frac{\partial {{\theta }_{e}}^{*}}{\partial x}\frac{\partial {{u}_{0}}}{\partial x}+{{v}_{e}}\frac{\partial {{\theta }_{e}}^{*}}{\partial y}\frac{\partial {{v}_{0}}}{\partial y} \\ \end{align} \right)$ | (A5) |
| $ {\mathit{\boldsymbol{{F}}}_{01}}=f{\mathit{\boldsymbol{{v}}}_{a0}}\times \nabla \theta _{0}^{*}$ | (A6) |
| $ {\mathit{\boldsymbol{F}}_{02}} = \left( \begin{array}{l} \left[ {\left( {{u_0}\frac{{\partial {\theta _e}^*}}{{\partial x}} + {v_0}\frac{{\partial {\theta _0}^*}}{{\partial y}}} \right)\frac{{\partial {u_0}}}{{\partial z}} - \left( {{u_0}\frac{{\partial {u_0}}}{{\partial x}} + {v_0}\frac{{\partial {u_0}}}{{\partial y}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right]\\ \left[ {\left( {{u_0}\frac{{\partial {\theta _0}^*}}{{\partial x}} + {v_0}\frac{{\partial {\theta _0}^*}}{{\partial y}}} \right)\frac{{\partial {v_0}}}{{\partial z}} - \left( {{u_0}\frac{{\partial {v_0}}}{{\partial x}} + {v_0}\frac{{\partial {v_0}}}{{\partial y}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right]\\ \left( {\left[ \begin{array}{l} \left( {{v_0}\frac{{\partial {u_0}}}{{\partial y}} + {w_0}\frac{{\partial {u_0}}}{{\partial z}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial x}} + \left( {{u_0}\frac{{\partial {v_0}}}{{\partial x}} + {w_0}\frac{{\partial {v_0}}}{{\partial z}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial y}} - \\ \left( {{v_0}\frac{{\partial {\theta _0}^*}}{{\partial y}} + {{\rm{w}}_0}\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right)\frac{{\partial {u_0}}}{{\partial x}} - \left( {{u_0}\frac{{\partial {\theta _0}^ * }}{{\partial x}} + {w_0}\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right)\frac{{\partial {v_0}}}{{\partial y}} \end{array} \right]} \right) \end{array} \right) $ | (A7) |
| $ {\mathit{\boldsymbol{F}}_{03}} = \left( \begin{array}{l} \left[ {\left( {{u_e}\frac{{\partial {\theta _e}^*}}{{\partial x}} + {v_e}\frac{{\partial {\theta _e}^*}}{{\partial y}}} \right)\frac{{\partial {u_0}}}{{\partial z}} - \left( {{u_e}\frac{{\partial {u_e}}}{{\partial x}} + {v_e}\frac{{\partial {u_e}}}{{\partial y}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right]\\ \left[ {\left( {{u_e}\frac{{\partial {\theta _e}^*}}{{\partial x}} + {v_e}\frac{{\partial {\theta _e}^*}}{{\partial y}}} \right)\frac{{\partial {v_0}}}{{\partial z}} - \left( {{u_e}\frac{{\partial {v_e}}}{{\partial x}} + {v_e}\frac{{\partial {v_e}}}{{\partial y}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right]\\ \left( {\left[ \begin{array}{l} \left( {{v_e}\frac{{\partial {u_e}}}{{\partial y}} + {w_e}\frac{{\partial {u_e}}}{{\partial z}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial x}} + \left( {{u_e}\frac{{\partial {v_e}}}{{\partial x}} + {w_e}\frac{{\partial {v_e}}}{{\partial z}}} \right)\frac{{\partial {\theta _0}^*}}{{\partial y}} - \\ \left( {{v_0}\frac{{\partial {\theta _e}^*}}{{\partial y}} + {{\rm{w}}_e}\frac{{\partial {\theta _0}^*}}{{\partial z}}} \right)\frac{{\partial {u_0}}}{{\partial x}} - \left( {{u_e}\frac{{\partial {\theta _e}^ * }}{{\partial x}} + {w_e}\frac{{\partial {\theta _e}^*}}{{\partial z}}} \right)\frac{{\partial {v_0}}}{{\partial y}} \end{array} \right]} \right) \end{array} \right)$ | (A8) |
式中,下标“0”代表基本态,下标“e”代表扰动态。
蔡则怡, 宇如聪, 1997. LASG限区域数值预报模式对一次登陆台风特大暴雨的数值试验[J]. 大气科学, 21(4): 459-471. |
陈永林, 王智, 曹晓岗, 等, 2009. 0509号台风(Matsa)登陆螺旋云带的增幅及其台前飑线的特征研究[J]. 气象学报, 67(5): 828-839. DOI:10.11676/qxxb2009.081 |
程正泉, 陈联寿, 徐祥德, 等, 2005. 近10年中国台风暴雨研究进展[J]. 气象, 31(12): 3-9. DOI:10.7519/j.issn.1000-0526.2005.12.001 |
程正泉, 林良勋, 沙天阳, 等, 2014. "尤特"特大暴雨过程的热力条件分析[J]. 气象, 40(12): 1507-1512. DOI:10.7519/j.issn.1000-0526.2014.12.009 |
冀春晓, 薛根元, 赵放, 等, 2007. 台风Rananim登陆期间地形对其降水和结构影响的数值模拟试验[J]. 大气科学, 31(2): 233-244. |
雷小途, 2002. 热带低压对上海"01.8.5"暴雨的作用[J]. 气象学报, 60(增刊): 52-57. |
康建伟, 陆汉城, 钟科, 等, 2007. 台风内部的中尺度波动与多边形眼墙的形成[J]. 热带气象学报, 23(1): 21-26. |
康岚, 牛俊丽, 徐琳娜, 等, 2013. 台风对四川暴雨影响的环境场对比分析[J]. 气象, 39(4): 427-435. DOI:10.7519/j.issn.1000-0526.2013.04.004 |
李波, 费建芳, 黄小刚, 等, 2011. 0908号台风"莫拉克"异常路径的诊断分析与数值模拟[J]. 海洋预报, 28(2): 18-22. DOI:10.11737/j.issn.1003-0239.2011.02.003 |
李英, 陈联寿, 2015. 湿地边界层通量影响热带气旋登陆维持和降水的数值试验[J]. 气象学报, 63(5): 683-693. |
李英, 陈联寿, 2006. 高空槽对9711号台风变性加强影响的数值研究[J]. 气象学报, 64(5): 552-563. DOI:10.11676/qxxb2006.054 |
李英, 陈联寿, 雷小途, 2013. Winnie(1997) 台风变性加强过程中的降水变化研究[J]. 大气科学, 37(3): 623-633. DOI:10.3878/j.issn.1006-9895.2012.11213 |
李英, 王继志, 陈联寿, 等, 2007. 台风麦莎(Matsa)的波状降水特征研究[J]. 科学通报, 53(2): 344-353. |
梁旭东, 端义宏, 陈仲良, 2002. 登陆台风的对流非对称结构[J]. 气象学报, 60(增刊): 26-35. |
刘峰, 丁治英, 梁艳, 等, 2011. "莫拉克"台风暴雨过程中湿位涡场的演变特征[J]. 暴雨灾害, 30(2): 161-166. |
钮学新, 杜惠良, 刘建勇, 2005. 0216号台风降水气象及其影响降水机制的数值模拟试验[J]. 气象学报, 63(1): 57-68. DOI:10.11676/qxxb2005.007 |
潘志祥, 方慈安, 黄小玉, 等, 2001. "玛丽亚"台风暴雨天气过程分析[J]. 气象, 27(8): 40-44. DOI:10.7519/j.issn.1000-0526.2001.08.009 |
沈杭峰, 高天赤, 周春雨, 等, 2014. 台风海葵引发浙西山区大暴雨的成因[J]. 气象, 40(6): 733-743. DOI:10.7519/j.issn.1000-0526.2014.06.010 |
文永仁, 魏娜, 张雪蓉, 等, 2014. 1323号强台风菲特登陆后迅速衰亡的原因分析[J]. 气象, 40(11): 1316-1323. DOI:10.7519/j.issn.1000-0526.2014.11.004 |
许娈, 何金海, 高守亭, 等, 2013. 集合动力因子对登陆台风"莫拉克"(0908) 暴雨落区的诊断与预报研究[J]. 大气科学, 37(1): 23-35. DOI:10.3878/j.issn.1006-9895.2012.11156 |
徐祥德, 张胜军, 陈联寿, 等, 2004. 台风涡旋螺旋波及其波列传播动力学特征:诊断分析[J]. 地球物理学报, 47(1): 33-41. |
袁子鹏, 王元, 陈艳秋, 等, 2006. 高空急流对黄渤海登陆热带气旋三维运动结构的影响[J]. 气象, 32(5): 3-9. DOI:10.7519/j.issn.1000-0526.2006.05.001 |
张建海, 黄汉中, 何勇, 2011. 台风"莫拉克"路径诊断分析和模拟[J]. 气象科技, 39(2): 182-189. |
曾智华, 陈伯民, 高泉平, 2002. 盛夏"城市热岛"对上海"01.8.5"特大暴雨影响的数值模拟[J]. 气象学报, 60(增刊): 58-64. |
周立, 李青青, 范轶, 等, 2011. 台风莫拉克、天鹅和艾涛的引导流及相互作用研究[J]. 中国海洋大学学报(自然科学版), (06). |
周冠博, 高守亭, 冉令坤, 2013. 台风"凤凰"强降水过程中的波作用诊断分析[J]. 大气科学学报, 36(1): 7-19. |
周玉淑, 邓涤菲, 李建通, 2014. 登陆热带气旋Bilis(0604) 暴雨增幅与风场结构变化[J]. 大气科学, 38(3): 563-576. DOI:10.3878/j.issn.1006-9895.2013.12220 |
Chen Lianshou, et al, 2006. Observations and Forecasts of Rainfall Distribution[M].
IWTC-VI: Topic 1.2, 36-42.
|
Gao S, Ran L. 2009. Diagnosis of wave activity in a heavy-rainfall event. J Geophys Res, 114, D08119, doi:doi:10.1029/2008JD010172.
|
Gao S, Wang X, Zhou Y. 2004.Generation of generalized moist potential vorticity in a frictionless and moist adiabatic flow. Geophys Res Lett, 31 L12113. doi:10.1029/2003GL019152.
|
Lindzen R S, Holton J R, 1968. A theory of the quasi-biennial oscillatinn[J]. J Atmos Sci, 25: 1095-1107. DOI:10.1175/1520-0469(1968)025<1095:ATOTQB>2.0.CO;2 |
Matsuno T, 1970. Vertical propagation of stationary planetary waves in the winter northern hemisphere[J]. J Atmos Sci, 27: 871-883. DOI:10.1175/1520-0469(1970)027<0871:VPOSPW>2.0.CO;2 |
Ran Lingkun, Yang Wenxia, Chu Yanli, 2010. Diagnosis of dynamic process over rainband of landfall typhoon[J]. Chin Phys B, 19(7): 611-623. |
Shepherd T G, 1990. Symmetries, conservation laws, and hamiltonian structure in geophysical fluid dynamics[J]. Adv Geophys, 32: 287-338. DOI:10.1016/S0065-2687(08)60429-X |
Pfeffer R L, 1992. A study of eddy-induced fluctuations of the zonal-mean wind using conventional and transformed Eulerian diagnostics[J]. J Atmos Sci, 49: 1036-1050. DOI:10.1175/1520-0469(1992)049<1036:ASOEIF>2.0.CO;2 |
 2015, Vol. 41
2015, Vol. 41 
