2. 成都信息工程学院大气科学学院,高原大气与环境四川省重点实验室,成都 610225;
3. 四川省气象台,成都 610072;
4. 空军装备研究院航空气象防化研究所,北京 100085;
5. 国家气象中心,北京 100081;
6. 中国科学院大气物理研究所云降水物理与强风暴实验室,北京 100029;
7. 中国科学院大学,北京 100049
2. College of Atmospheric Sciences, Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology, Chengdu 610225;
3. Sichuan Meteorological Observatory, Chengdu 610072;
4. Institute of Aeronautical Meteorology and Chemical Defense, Equipment Academy of Air Force, Beijing 100085;
5. National Meteorological Centre, Beijing 100081;
6. Key Laboratory of Cloud-Precipitation Physics and Severe Storms, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
7. University of Chinese Academy of Sciences, Beijing 100049
众所周知,天气预报是存在不确定性的(Candille et al,2008)。随着数值预报技术的发展,降水预报的准确率得到了一定程度的提高(刘莹等,2013)。为了定量估计数值天气预报的不确定性,数值天气预报已经由单一值的确定性预报进入到集合预报时代。集合预报是近20年来迅速发展并广泛应用的一种数值预报方法(陈静等,2002)。相对于单一的确定性预报,它考虑了初值及模式的不确定性,可以发挥多成员预报的优势,提供包含不确定性的概率预报,提高数值预报的可用性。交互式全球大集合TIGGE(THORPEX Interactive Grand Global Ensemble)作为THORPEX的科学研究计划的一项重要内容,其资料目前已在概率降水预报、水文预报及集成降水预报等方面得到了广泛的应用(Zhao et al,2011;2012;赵琳娜等,2012;Liang et al,2012;Bao et al,2012;包红军等,2012;狄靖月等,2013;姜迪等,2014;Gneiting et al, 2005;段明铿等,2004;刘建国等,2013)。
降水预报是天气预报中具有挑战性的一项工作,对预报结果进行评估是降水预报工作中的一个重要环节(Carlos et al,2012)。目前国际上采用的集合预报检验方法主要有Talagrand分布、TS评分、Hedike评分、Brier评分、相对作用特征曲线(ROC曲线)、连续分级概率评分和可靠性曲线等方法。在评估环节中,要求用于预报评估的实况观测尽可能准确。在结合降水实况对预报能力进行技术评分时,通常人们只考虑了集合预报的不确定性,而假设观测的实况降水是准确的。然而,不同的实况观测的处理方法带来的不确定性也是存在的。
针对分析集合预报结果不确定性的主要原因方面,国内外学者在初始场的不确定性、模式的不确定性以及预报的不确定性方面有了比较多的研究(Toth et al,1997;朱跃建等,1998)。有关降水观测的不确定性对于预报检验的影响,国内外有些学者做过相应的探索。Ciach等(1999) 曾用测量误差来定义不确定性。Briggs等(2005)和Roberts等(2008) 用观测误差的错误分类来定义不确定性。Saetra等(2004) 通过将带有预定义的标准差的高斯分布噪声附加到预报的每个集合成员,研究了观测误差对集合平均和可靠性的影响。Pappenberger等(2009) 认为观测不确定性源于以下几类:测量误差、观测密度的不均匀和模型或观测的插值。而观测资料除了观测误差之外还有很大的不确定性(梁莉等,2011),其中降水资料的分布随机性是最为突出的,尤其是在极端降水天气出现的时候(张婷,2009)。Candille等(2008) 提出了一种经验观测法来获得观测不确定性。王芳等(2007) 指出,产生观测数据不确定性原因包括观测网络覆盖度低、单元格内数据源分布不均匀、大量站点观测连续性差、站点大部分位于大城市等。但并没有提出解决这些问题的具体方案。而且这些不确定性的研究大多与观测误差联系在一起。在进行预报评分时,由于模式格点与实况观测站点的位置不匹配,在插值过程中也会产生的不确定性。如何估计这种不确定性对预报评估的影响则成为了一个亟待解决的问题。因此,本文拟采用对降水观测资料不同的处理方法来获得观测资料的不确定性,分析不同的降水观测资料处理方法对于不同的降水量级预报评估的影响,从而分析观测不确定性对集合预报评估的影响。
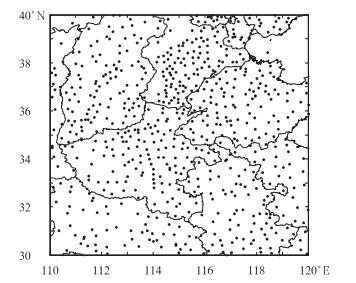
1 研究区域及资料本文的研究区域为我国东部的淮河区域(30°~40°N、110°~120°E)。观测资料采用该区域2008年1月1日至2010年12月30日内652个站点的逐日降水量资料。选取前一日12:00至当日12:00时(世界时)的降水量作为当日24 h累积降水量。预报资料为参加TIGGE计划的中国T213集合预报系统同时段的24 h累积降水预报。该集合预报系统有15个成员,空间分辨率为0.5625°×0.5625°。
2 方法 2.1 预报和观测资料的处理方法在预报结果和观测资料都不改变的情况下,改进检验中观测资料处理方法,减小观测资料处理过程中产生的不确定性,考察检验中观测资料处理方法对降水预报评估效果的影响是本文的研究目的。
|
图 1 研究区域及区域内降水观测站的分布 Fig. 1 Illustration of research area and locations of relevant observing stations |
将T213集合预报系统的15个成员视为等权重预报,对于每一个模式格点,将24 h累积降水预报分为5个阈值进行检验,即0.1、5、10、15和25 mm。对于某一阈值若预报有雨记为1,无雨记为0。该格点某个阈值降水事件发生预报概率就是预报有雨的成员数除以总成员数。
检验就是预报概率与该格点的观测资料进行比较。集合预报作为概率预报的一个分类,其对于某个格点的预报结果可以是0~1任何数值。
2.1.2 观测资料不确定性的表达方法(1) 参考法
参考法就是传统的集合预报评估中观测资料处理方法,该方法计算模式格点上的降水观测概率时,通常取1或0。即对于某一阈值的降水事件,记po为观测概率,事件发生则观测概率po为1,事件不发生则po为0。此方法对应模式格点上的观测为1或0。为叙述简便,本文中将这种方法称为参考法(简称REF法,下同)。
(2) 观测概率法
由于站点分布与模式格点并不匹配,观测资料在格点化处理过程中会产生不确定性,影响甚至降低预报的评分结果。理论上,观测概率可为0~1的任何数值,因此,参考法存在一定的缺点。为克服上述缺陷,本文设计一种新的观测资料处理方法——观测概率法(简称OP法,下同)。这种方法是将模式格点的方格内发生某一阈值降水事件的站点数除以方格内的总站点数。用此方法处理的观测概率为0~1的任何数值。
(3) 观测百分位数法
考虑到测站在研究区域内分布的不均匀性,本文设计了模式格点上的观测概率的另一种方法。这种方法是将格点的方格内的所有站点按照降水量由小到大的顺序排列,计算出降水量相应的累积百分位,则百分位所对应的数值就称为这一百分位的百分位数。计算与某降水阈值相邻的两个站的百分位数,这两个概率的平均,看做该格点的观测概率。对于两端事件,当所有站点都在某一事件降水阈值范围之内时,概率为1;反之为0。具体为:
以某一站点降水量Xa(k)为阈值X的概率为P,其百分位数为a(k),则
| $ \begin{align} &P\left(\text{X}<{{X}_{a\left(k \right)}} \right)=a\left(k \right) \\ &P\left(\text{X}>{{X}_{a\left(k \right)}} \right)=a\left(k-1 \right) \\ \end{align} $ |
| $计算一给定降水阈值t事件发生的概率,即:$ \begin{align} &{{X}_{a\left(k-1 \right)}}\le t\le {{X}_{a\left(k \right)}}, \\ &P\left(X<{{X}_{a\left(k-1 \right)}} \right)\le P\left(X<t \right)\le P\left(X<{{X}_{a\left(k \right)}} \right), \\ &P\left(X>{{X}_{a\left(k-1 \right)}} \right)\ge P\left(X<t \right)\ge P\left(X<{{X}_{a\left(k \right)}} \right); \\ &1-a\left(k-1 \right)\ge P\left(X<t \right)\ge 1-a\left(k \right) \\ \end{align} $ 因此,对于观测概率po=P(X>t),若只简单等于概率P(X>Xa(k-1))或P(X>Xa(k)),则会高估或低估po。因此,将两个概率求平均的结果,看做事件t发生的概率。$ |
| $ \begin{align} &{{p}_{o}}=P\left(X>t \right)\approx \left[ P\left(X>{{X}_{a\left(k-1 \right)}} \right) \right]+P\left(X>{{X}_{a\left(k \right)}} \right)/2 \\ &\ \ \ \ =1-\left[ a\left(k \right)+a\left(k-1 \right) \right]/2 \\ \end{align} $ |
对于两端事件,当所有站点都在某一事件降水阈值范围之内时,po为1;反之则po为0。此方法对于格点内站点稀少时优势较大。这种方法记为观测百分位数法(简称OPC法,下同)。
OP、OPC与REF法相比,虽也无法完全准确描述模式格点的观测概率,但概率的表达形式更贴近实际的各种可能值以及其发生的概率,特别是在做多阈值降水预报评估时[如预报的降水概率为0.6,本文的OP、OPC法计算的观测概率为0.7,比REF法中对观测的取值为有或无(即1或0)]更接近实际情况,从而使观测不确定性减小,得到的评分更为合理可靠。
2.2 检验方法 2.2.1 Brier评分Brier评分(BS)定义了一种均方概率误差,该方法综合考虑了可靠性、分辨性和不确定性。Brier评分已在定量降水概率预报评估中得到了广泛应用(Ferro,2007;赵琳娜等,2010;2014)。
| $ BS=E\left[ {{\left(p-{{p}_{\text{o}}} \right)}^{2}} \right] $ | (1) |
式中,p为事件发生的预报概率,po表示实况。事件发生po为1,事件不发生po为0,在这一形式中, BS范围是0~1,且越小越好,即BS为0表示概率预报最佳,预报正确;BS为1,表示评分最差,预报失效(Zhao et al,2011)。本研究中,当使用REF法时,po为0或1。当使用OP及OPC法时,po范围为0~1。
2.2.2 Brier技巧评分Brier技巧评分(BSS)是基于Brier评分的技巧评分,其公式定义为:
| $ BSS=1-BS/B{{S}_{\text{clim}}} $ |
Brier技巧评分通常的表现形式为:
| $ BSS=BSS\_res-BSS\_rel $ |
式中,BSS_rel为可靠性项,BSS_res为分辨率项。
本文涉及到的Brier技巧评分为两种,分别为标准的Brier技巧评分,以及为适应OP及OPC法而对标准Brier技巧评分做相应改动的扩展Brier技巧评分。
标准的Brier技巧评分推导过程为
| $ BS=E\left[ {{\left(p-{{p}_{\text{o}}} \right)}^{2}} \right] $ |
其中po为0或1
当任意事件p′发生时,
| $ \begin{align} &{{E}_{p}}\left[ {{\left({{p}^{'}}-{{p}_{\text{o}}} \right)}^{2}} \right]=p{{'}^{2}}-2{{p}^{'}}\left[ {{p}_{\text{o}}} \right]+{{E}_{p}}\left[ {{p}_{\text{o}}}^{2} \right] \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\left({{p}^{'}}-{{E}_{p}}{{\left[ {{p}_{\text{o}}} \right]}^{2}} \right)+{{E}_{p}}\left[ {{p}_{\text{o}}}^{2} \right]-{{E}_{p}}{{\left[ {{p}_{\text{o}}} \right]}^{2}} \\ \end{align} $ | (2) |
因为po为0或1,
| $ \ {{E}_{p}}\left[ {{p}_{\text{o}}}^{2} \right]\ ={{E}_{p}}\left[ {{p}_{\text{o}}} \right]\ $ |
令p′(p)=Ep[po]
| $ {{E}_{p}}\left[ {{\left({{p}^{'}}-{{p}_{\text{o}}} \right)}^{2}} \right]={{\left[ {{p}^{'}}-{{p}^{'}}\left(p \right) \right]}^{2}}+{{p}^{'}}\left(p \right)\left[ 1-{{p}^{'}}\left(p \right) \right] $ |
将所有预报再做平均,令E[p′(p)]=pc=E[po]
| $ BS=E\left[ {{\left( {p}'-{p}'\left( p \right) \right)}^{2}} \right]-E\left[ {{\left( {p}'\left( p \right)-{{p}_{\text{c}}} \right)}^{2}} \right]+{{p}_{\text{c}}}\left( 1-{{p}_{\text{c}}} \right) $ | (3) |
式中,BSref=pc(1-pc)
| $ BSS=1-\frac{BS}{{{p}_{\text{c}}}\left( 1-{{p}_{\text{c}}} \right)} $ |
| $ BSS=\frac{E\left[ {{\left( {p}'\left( p \right)-{{p}_{\text{c}}} \right)}^{2}} \right]-E\left[ {{\left( {p}'-{p}'\left( p \right) \right)}^{2}} \right]}{{{p}_{\text{c}}}\left( 1-{{p}_{\text{c}}} \right)} $ | (4) |
| $ BSS=\text{BSS}\_res-BSS\_rel $ | (5) |
| $ BS{{S}_{\_res}}=\frac{E\left[ {{\left( {p}'\left( p \right)-{{p}_{\text{c}}} \right)}^{2}} \right]}{{{p}_{\text{c}}}\left( 1-{{p}_{\text{c}}} \right)}$ | (6) |
| $ BS{{S}_{\_rel}}=\frac{E\left[ \left( {p}'-{p}'{{\left( p \right)}^{2}} \right) \right]}{{{p}_{\text{c}}}\left( 1-{{p}_{\text{c}}} \right)} $ | (7) |
式中,Ep代表当p′发生时的条件期望,pc代表气候概率,pc(1-pc)为BS评分的不确定性项。由于在推导的过程中,po为0或1,因此标准的Brier技巧评分公式只适用于REF法。Brier技巧评分是表示预报对气候预报的改进程度。若BSS为0,则BSS评分为气候值。若某事件的概率预报的BSS大于0,则它的预报才有意义;反之,则该事件的概率预报不如气候概率,因此,Brier技巧评分越大越好。
由于本文考虑了观测的概率,即当po为0~1时,则使用扩展的Brier技巧评分(Carlos et al,2012)。扩展的Brier技巧评分推导过程为:
| $ {{E}_{p}}\left[ {{\left({{p}^{'}}-{{p}_{\text{o}}} \right)}^{2}} \right]={{\left({{p}^{'}}-{{E}_{p}}\left[ {{p}_{\text{o}}} \right] \right)}^{2}}+{{E}_{p}}\left[ p_{\text{o}}^{2} \right]-{{E}_{p}}{{\left[ {{p}_{\text{o}}} \right]}^{2}} $ |
| $ BS=E\left[ {{\left({{p}^{'}}-{{E}_{p}}\left[ {{p}_{\text{o}}} \right] \right)}^{2}} \right]+E\left[ {{E}_{\text{o}}}\left[ p_{\text{o}}^{2} \right]-{{E}_{p}}{{\left[ {{p}_{\text{o}}} \right]}^{2}} \right] $ |
令p′(p)=Ep[po]
| $ BS=E\left[ {{\left({{p}^{'}}-{{p}^{'}}\left(p \right) \right)}^{2}} \right]+E\left[ {{E}_{\text{o}}}\left[ p_{\text{o}}^{2} \right]-{{p}^{'}}{{\left(p \right)}^{2}} \right] $ |
定义
| $ \begin{align} & E\left[ {{x}^{2}} \right]-{{E}^{2}}\left[ x \right]={{E}_{j}}\left[ {{E}_{i}}\left[ {{x}^{2}} \right] \right]-{{E}_{j}}\left[ E_{i}^{2}\left[ x \right] \right]+{{E}_{j}}\left[ E_{i}^{2}\left[ x \right] \right]-E_{j}^{2}\left[ {{E}_{i}}\left[ x \right] \right] \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{E}_{j}}\left[ E_{i}^{2}\left[ x \right]-E_{i}^{2}\left[ x \right] \right]+{{E}_{j}}\left[ E_{i}^{2}\left[ x \right] \right]-E_{j}^{2}\left[ {{E}_{i}}\left[ x \right] \right] \\ \end{align} $ |
| $ BS=E\left[ {{\left( {p}'-{p}'\left( p \right) \right)}^{2}} \right]-E\left[ {{\left( {p}'\left( p \right)-{{p}_{c}} \right)}^{2}} \right]+E\left[ p_{\text{o}}^{2} \right]-p_{\text{c}}^{2} $ |
| $ BSS=1-\frac{BS}{E\left[ p_{\text{o}}^{2} \right]-p_{\text{c}}^{2}} $ |
| $ BSS=\frac{E\left[ {{\left[ {{p}^{'}}\left(p \right)-{{p}_{c}} \right]}^{2}} \right]-E\left[ {{\left[ {{p}^{'}}-{{p}^{'}}\left(p \right) \right]}^{2}} \right]}{E\left[ p_{c}^{2} \right]-p_{c}^{2}} $ | (8) |
| $ BSS=BS{{S}_{\_res}}-BS{{S}_{\_ref}} $ | (9) |
| $ BS{{S}_{\_res}}=\frac{E\left[ {{\left({{p}^{'}}\left(p \right)-{{p}_{\text{c}}} \right)}^{2}} \right]}{E\left[ p_{\text{o}}^{2} \right]-p_{\text{c}}^{2}} $ | (10) |
| $ BS{{S}_{\_rel}}=\frac{E\left[ {{\left({{p}^{'}}-{{p}^{'}}\left(p \right) \right)}^{2}} \right]}{E\left[ p_{\text{o}}^{2} \right]-p_{\text{c}}^{2}} $ | (11) |
因此,若用OP和OPC法处理的观测资料,则须使用扩展的Brier技巧评分。将Brier技巧评分和扩展的Brier技巧评分的可靠性项和分辨性项进行对比,由式(6)、(10)和式(7)、(11) 对比可以看出,两者的分辨性项和可靠性项区别在于分母部分,即标准的Brier技巧评分中的pc(1-pc)在扩展的Brier技巧评分中体现为E[pc2]-pc2。原因是此时的po的取值范围不再局限于0或1,而为0~1,并且两者的pc也不同。因此从公式可以看出,考虑观测误差后,可靠性部分变差了,分辨性部分变好了,这决定了总的Brier技巧评分降低或提高的程度。
3 结果分析首先分析三种不同的计算降水观测概率的方法,五个不同阈值的降水概率分布的变化。然后,分析不同的计算降水观测概率的方法对集合预报概率降水评分的影响,为分析使用REF、OP和OPC法处理的降水观测概率在不同量级降水评分中的表现,本文参照中国气象局2012年发布的降水量等级划分标准(国家气象中心,2012),将24 h降水分成0.1、5、10、15和25 mm五个等级,分别运用Brier评分和Brier技巧评分,对集合预报系统的不同等级降水预报进行评估。在本研究3年的观测资料中,大雨以上量级的降水出现的频次较少,因此本文在评分中未对暴雨以上量级的降水进行评估,而增加了对阈值为5和15 mm降水的评估,表 1列出了2008年1月1日至2010年12月30日24 h累积降水观测各降水阈值的样本数。
|
|
表 1 2008年1月1日至2010年12月30日24 h累积降水预报各降水阈值样本 Table 1 Sample the numbers of five thresholds for 24 h accumulated rainfall forecasts from 1 January 2008 to 30 December 2010 |
以下就是利用本文所述的三种观测资料处理方法(REF、OP和OPC法),将观测资料插值到模式格点上后,对集合预报的五个降水预报阈值进行检验。具体是:首先对每个降水阈值的3年的总样本数进行检验,对于每个观测资料的处理方法,每天14×14个格点的预报,3年共214620个格点的预报进行检验。其次为了区分检验结果在各月的表现,对于每个阈值每个月都分别进行了检验,就是将3年的各月的观测资料提取出来,同时将3年中对应月的集合预报提取出来检验得到每个月的评分。
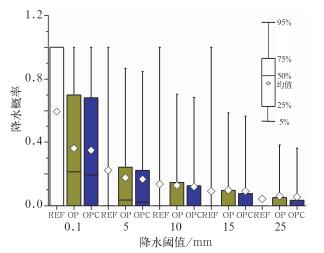
3.1 不同方法处理后观测降水概率的分布盒须图可以用来研究数据的分布情况。图 2是用不同的计算方法得到的五个阈值的降水观测概率盒须图。图 2的盒须图从下往上分别是第5、25、50、75和95百分位,中间空心菱形为均值,所有序列的最大和最小均为1.0和0.0。从图 2可以看到,不论哪种方法处理的降水观测概率,随着降水阈值的增大,盒须图的拉伸度逐渐缩小,并且集中在概率低的一侧。这说明降水概率分布紧凑离散度小,且大部分降水概率向较低概率一侧倾斜。无论对于0.1、5.0、10.0、15.0和25.00 mm哪个阈值的降水,比较REF、OP和OPC法处理的降水观测概率,OPC法计算的降水概率均比REF和OP法的概率分布紧凑和集中,OP法概率分布较集中,REF法是概率分布最分散的。其次还可以看出,对每个降水阈值来说,REF法计算的降水概率范围变化最大,OPC法计算的降水概率范围变化最小。此外,大部分降水概率向降水概率低的一侧靠近。总的来说,REF法得到的降水概率离散度较大。
|
图 2 不同方法计算的五个降水阈值观测概率的分布 (盒须图从下往上分别是第5、25、50、75和95百分位,中间空心菱形为均值) Fig. 2 The distribution of observation probability estimated by REF, OP and OPC methods for five thresholds of prediction, respectively (The box-and-whisker plots indicate the 5th, 25th, 50th, 75th and 95th percentile precipitation, respectively; the hollow diamond stands for average value) |
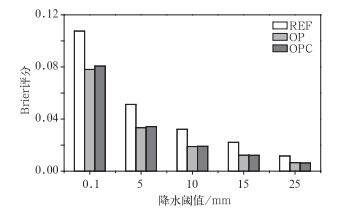
图 3为采用三种不同的观测资料处理方法对中国集合预报系统五个不同阈值降水预报进行的Brier评分比较。其中,REF法中的观测值po是在相应降水阈值条件下的0或1的观测结果,OP和OPC法的po则是0~1的一个观测概率。从图 3中可以看出,采用了本文设计的OP和OPC法对观测资料处理后的Brier评分,在所有降水阈值范围内,OP和OPC法的Brier评分分值都要低于REF法的评分分值,说明考虑了观测资料的不确定性之后,集合预报性能提高。其中,对于小到中等强度的降水预报(即降水阈值为0.1、5、10和15 mm)评分时,新的观测资料处理方法使集合预报的预报效果提高的优势更明显。对于阈值为25 mm(即大雨以上量级)的降水,新方法虽然较REF法提高了集合预报的性能,但是由于降水事件发生的次数随着阈值的提高而明显减少,因此提高的幅度没有中等量级的预报效果大,即使如此,随着降水阈值的提高,三种方法的Brier评分值都减小,说明考虑了观测的不确定性后,集合预报系统在所有的降水阈值的预报都更加准确了。另外从图 3中还可以看出,OP和OPC法这两种新方法相比差别不大。下面将进一步深入分析采用Brier技巧评分以及改进的Brier技巧评分后,三种方法所得到的评分结果的异同。
|
图 3 REF、OP和OPC三种处理降水观测资料的方法对不同降水阈值预报的Brier评分 Fig. 3 Brier scores of five precipitation threshold forecasts using REF, OP and OPC methods |
根据前面的分析可知概率预报的Brier技巧评越大越好。BSS大于0,说明它的预报才有意义,表明预报比气候概率好。图 4为采用三种不同的观测资料处理方法对中国集合预报系统五个不同阈值降水预报进行的Brier技巧评分比较。由图 4中可以看出,集合预报系统五个不同阈值降水预报OPC法的Brier技巧评分分值在所有降水阈值中都要高于OP而低于REF法,同时OP和OPC这两种新的方法均不如REF法预报技巧高。REF法随着降水阈值的增大,BSS评分逐渐降低;而OP和OPC法BSS评分随降水阈值的变化不大,说明使用新方法评价后预报系统比较稳定。从整体上看,相对于气候概率,都有预报意义。

|
图 4 REF、OP和OPC三种处理观测资料的方法对不同降水阈值预报的Brier技巧评分 Fig. 4 Brier skill scores of five precipitation threshold forecasts using REF, OP and OPC methods |
为了进一步细致分析本文设计的方法对Brier技巧评分的影响,本文又考察了每个月预报的Brier技巧评分。另外从图 3中还可以看出,OP和OPC这两种新方法相比差别不大。因此,下面将重点对比分析REF和OPC法对于预报阈值为0.1、5、10、15以及25 mm的24 h累积降水预报Brier技巧评分的影响在各月的变化。
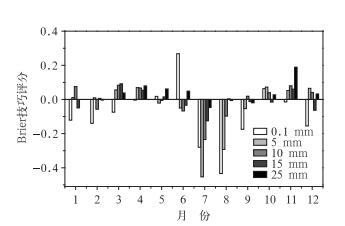
计算每月各阈值降水预报的Brier技巧评分,为了便于比较OPC与REF法,图 5中给出了OPC法的Brier技巧评分与REF法的Brier技巧评分之差。需要说明的是本文研究的格点数据中1月没有出现25 mm以上的降水,因此图 5、图 7和图 9中1月25 mm的降水评分没有值。由图 5中可以看出,0.1 mm的24 h累积降水预报阈值评分,5、6、10月OPC法的Brier技巧评分分数要高于REF法,更有预报技巧;5 mm的24 h累积降水预报阈值的Brier技巧评分,1—4月、10—12月OPC法的Brier技巧评分分数要高于REF法,更有预报技巧;10 mm的24 h累积降水预报阈值的Brier技巧评分,1、3、4月、9—12月OPC法的Brier技巧评分分数要高于REF法,更有预报技巧;15 mm的24 h累积降水预报阈值的Brier技巧评分,2—5月、11月OPC法的Brier技巧评分分数要高于REF法,更有预报技巧;25 mm的24 h累积降水预报阈值的Brier技巧评分,3—6、10—12月OPC法的Brier技巧评分分数要高于REF法,更有预报技巧。因此总体上来看,集合预报系统在0.1、5、10、15以及25 mm五个24 h累积降水阈值中,OPC法在冬季、春季和秋季的Brier技巧评分分数高于REF法,更有预报技巧;夏季6—8月五个降水阈值预报的OPC法Brier技巧评分低于REF法。因此可以看出,中国集合预报系统,OPC法在夏季较低的Brier技巧评分抵消了在其他三个季节的优势,因此全年Brier技巧评分(图 5) 无法体现OPC法的优势。
|
图 5 五个降水阈值预报(OPC法-REF法)的Brier技巧评分逐月变化 Fig. 5 Monthly variation of Brier skill scores of five precipitation threshold forecasts(OPC-REF) |
|
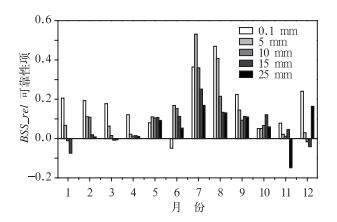
图 7 五个降水阈值预报(OPC-REF法)的Brier技巧评分可靠性的逐月变化 Fig. 7 Monthly variation of Brier skill score reliability of five precipitation threshold forecasts using OPC-REF method |
|
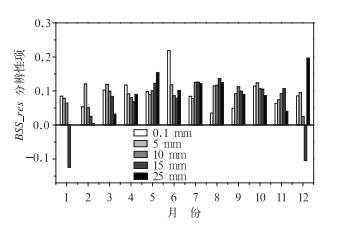
图 9 个降水阈值预报(OPC-REF法)的Brier技巧评分分辨性的逐月变化 Fig. 9 Monthly variation of Brier skill score resolution of for five precipitation threshold forecasts by OPC-REF method |
为了深入探讨,考虑了观测的随机性后新的评分方法对Brier技巧评分分辨性和可靠性的影响,下面将按照Brier技巧评分式(9) 的分解,分别讨论OPC和REF法的对Brier技巧评分的可靠性[式(10)]与分辨性[式(11)]的影响。
3.3.2 集合预报系统可靠性的分析可靠性表示预报概率与样本中该事件发生频数的一致程度。图 6为观测采用了OPC与REF法后,集合预报系统的可靠性分析。由前面2.1.2节有关可靠性项的分析可知,可靠性项的值越大,表示某个阈值预报的可靠性越小。由图 6中可以看出,对于集合预报系统在五个降水阈值的评分中,使用了OPC法后模式的可靠性都要低于REF法。也就是说使用考虑了观测的随机性后,集合预报系统在五个降水阈值预报Brier技巧评分的可靠性变低。分析其原因,考虑了观测的随机性后,与式(6)和(7) 相比,式(10)和(11) 中po的取值范围不再局限于0或1,而为0~1,并且两者的pc也不同。因此考虑观测误差后,可靠性部分变差了。下面将深入分析每个月模式的Brier技巧评分的可靠性,结果如图 7所示。

|
图 6 采用REF和OPC法集合预报的Brier技巧评分可靠性 Fig. 6 Reliability of Brier skill scores of ensemble forecast thresholds using REF and OPC methods |
图 7给出了OPC法的Brier技巧评分与REF法的Brier技巧评分可靠性的逐月变化之差。从图 7中可以看出,集合预报系统0.1、5、10、15和25 mm的24 h累积降水阈值预报的可靠性在各月存在明显的变化。对于0.1、5 mm阈值的24 h累积降水预报,OPC法的中国集合预报系统可靠性在全年各月比REF略低,10 mm降水阈值24 h累积预报的在1和12月OPC法的可靠性比REF法的要高,对于15 mm阈值的24 h累积降水预报,OPC法的在12月和1、3月可靠性增加了,对于25 mm阈值的24 h累积降水预报,OPC法的在11、3月可靠性增加了。
总体来讲,当使用了OPC法后,夏季和冬季的各降水阈值预报可靠性比REF法低,尤其是夏季。说明观测考虑了不确定性了以后,集合预报系统的可靠性下降了。对比0.1、5、10、15和25 mm降水阈值24 h累积降水预报可靠性可以看出,降水阈值为25 mm的预报可靠性,OPC和REF法差别的变化幅度最小(图 7)。
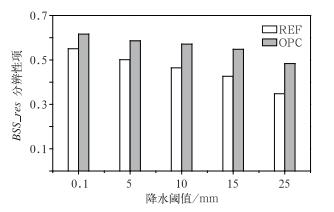
3.3.3 集合预报系统分辨性的分析分辨性是一种度量在子样本中,事件相对频率与总样本中事件相对频率(如气候概率)区别程度的度量。图 8为采用OPC与REF法后,集合预报系统的Brier技巧评分分辨性的分析。使用了OPC法后,集合预报系统的分辨性在0.1、5、10、15、25 mm降水阈值预报中都要高于REF法,说明采用了观测的不确定性后的评分法(OPC法)比REF法的分辨能力更高。
|
图 8 采用REF法和OPC法集合预报的Brier技巧评分分辨性 Fig. 8 Resolution of Brier skill score of ensemble precipitation forecast thresholds using REF and OPC methods |
分辨性项各月的演变如图 9所示。图 9给出了OPC法的Brier技巧评分与REF法的Brier技巧评分分辨性的逐月变化之差。由图 9中可以看出,五个降水阈值预报的分辨性在各月也存在明显的变化,但是无论在哪个月,采用了OPC法的分辨性要普遍高于REF法。只有15 mm降水阈值预报在1和12月的分辨性OPC低于REF法。
与OPC法在可靠性中的表现不同的是,OPC法比REF法的分辨性高的优势在全年保持得比较稳定。对比0.1、1、5、10、15和25 mm阈值24 h累积降水预报的可分辨性可知,各降水预报阈值之间的分辨性没有太大的差别(图 9)。
综合考察可靠性与分辨性可以看出,OPC法降低了夏季可靠性,普遍提高了全年0.1、5、10、15和25 mm降水阈值预报的分辨性。因此OPC方法的Brier技巧评分在夏季比REF方法低,但在春季和秋季比REF法的Brier技巧评分要高。
4 结论与讨论随着集合数值预报在天气气候预测中的广泛应用,如何评价一个预报的性能也提出了更高的要求,对于集合预报的使用者来讲,需要了解集合数值预报各个方面的表现。本文在通常的观测资料处理方法的基础上建立了观测概率法和观测百分位法两种新的观测资料的处理方法,并对相应的评分公式加以改进,目的就是在评估环节中考虑观测资料不同处理方法带来的不确定性,并与通常的处理方法(REF法)进行对比,讨论了不同方法对Brier评分、Brier技巧评分以及Brier技巧评分的可靠性与分辨性的影响,通过分析得到以下结论:
(1) 对于0.1、5、10、15和25 mm五个阈值的降水,比较REF、OP和OPC法处理的降水观测概率,OPC法计算的降水概率均比REF和OP法的概率分布紧凑和集中,OP法概率分布较集中,REF法是概率分布最分散的。其次还可以看出,对每个降水阈值来说,REF法计算的降水概率范围变化最大,OPC法计算的降水概率范围变化最小。此外,大部分降水概率向降水概率低的一侧靠近。总的来说,REF法得到的降水概率离散度较大。
(2) 考虑了观测不确定性对集合预报的评估是有一定影响的。这种影响首先表现在Brier评分中。采用了观测概率法和观测百分位法的评分在0.1、5、10、15和25 mm五个降水阈值中都要略高于参考法,尤其在中低降水阈值区域较为明显。
(3) 考虑了观测不确定性的OPC法与参考法集合预报评分结果相比,五个降水阈值预报的Brier技巧评分也是有一定差别的。OPC法在夏季的预报技巧低于REF法;而在春季和秋季中,OPC法在五个降水阈值预报的预报技巧不同程度比REF法高。这种预报技巧的提高在中等强度的降水中相对明显。这对以后如何考虑季节、降水阈值等因素,进一步改进评分方法提供了参考。
(4) 对Brier技巧评分可靠性和分辨性的分析表明,OPC法虽然降低了夏季的可靠性,但普遍提高了全年0.1、5、10、15和25 mm降水阈值预报的分辨性,因此OPC方法的Brier技巧评分在夏季比REF方法低,但在春季和秋季比REF法的Brier技巧评分要高。本文探索研究了集合预报评分中对观测资料处理方法,在观测资料的处理中考虑了观测资料的不确定性,并分析了该方法对集合预报技巧、可靠性、分辨性所产生的影响。应该指出的是,任何一种评分方法都是有局限性的,一种检验评估方法只能是给出预报产品的一个或几个方面的信息。本文修订的评分方法的特点是在观测资料中考虑了处理观测资料的不确定性,因此,对集合预报技术的研究和业务应用有着重要的意义。
需要指出的是,本研究讨论了站点等权重的观测资料处理方法,今后工作可以考虑非等权重的处理方法,还可以讨论站点分布不均匀程度对新方法评分的影响等。此外,本文只讨论了24 h累积降水预报,今后可考察预报时效为48 h或更长的降水预报。
包红军, 赵琳娜, 2012. 基于集合预报的淮河流域洪水预报研究[J]. 水利学报, 43(2): 216-224. |
陈静, 陈德辉, 颜宏, 2002. 集合数值预报发展与研究进展[J]. 应用气象学报, 13(4): 497-507. |
狄靖月, 赵琳娜, 张国平, 等, 2013. 降水集合预报集成方法研究[J]. 气象, 39(6): 691-698. DOI:10.7519/j.issn.1000-0526.2013.06.004 |
段明铿, 王盘兴, 2004. 集合预报方法研究及应用进展综述[J]. 南京气象学院学报, 27(2): 279-288. |
国家气象中心. 2012. GB/T28592-2012降水量等级国家标准.
|
姜迪, 智海, 赵琳娜, 等, 2014. 通用线性模型在气象水文集合预报后处理中的应用[J]. 大气科学学报, 37(2): 229-236. |
梁莉, 赵琳娜, 巩远发, 等, 2011. 淮河流域汛期20d内最大日降水量概率分布[J]. 应用气象学报, 22(4): 421-428. DOI:10.11898/1001-7313.20110404 |
刘建国, 谢正辉, 赵琳娜, 等, 2013. 基于TIGGE多模式集合的24小时气温BMA概率预报[J]. 大气科学, 37(1): 43-53. DOI:10.3878/j.issn.1006-9895.2012.11232 |
刘莹, 赵琳娜, 段青云, 等, 2013. 一种由单值预报生成定量降水概率预报的方法及初步应用[J]. 气象, 39(3): 313-323. DOI:10.7519/j.issn.1000-0526.2013.03.005 |
王芳, 葛全胜, 陈泮勤, 2007. IPCC评估报告气温变化观测数据的不确定性分析[J]. 地理学报, 64(7): 828-838. |
张婷, 魏凤英, 2009. 华南地区汛期极端降水的概率分布特征[J]. 气象学报, 67(3): 442-451. DOI:10.11676/qxxb2009.044 |
赵琳娜, 吴昊, 田付友, 等, 2010. 基于TIGGE资料的流域概率性降水预报评估[J]. 气象, 36(7): 133-142. DOI:10.7519/j.issn.1000-0526.2010.07.020 |
赵琳娜, 包红军, 田付友, 等, 2012. 水文气象研究进展[J]. 气象, 38(2): 129-146. DOI:10.11898/1001-7313.20120201 |
赵琳娜, 刘莹, 党皓飞, 等, 2014. 集合数值预报在洪水预报中的应用进展[J]. 应用气象学报, 25(6): 641-653. DOI:10.11898/1001-7313.20140601 |
朱跃建, 管兆勇, 王盘兴, 1998. 美国国家环境预测中心集成预报介绍[J]. 气象教育与科技, 20(1): 1-9. |
Bao Hongjun, Zhao Linna, 2012. Development and application of an atmospheric-hydrologic hydraulic flood forecasting model driven by TIGGE ensemble forecasts[J]. Acta Meteor Sin, 26(1): 93-102. DOI:10.1007/s13351-012-0109-0 |
Briggs W, Pocernich M, Ruppert D, 2005. Incorporating misclassification error in skill assessment[J]. Mon Wea Rev, 133: 3382-3392. DOI:10.1175/MWR3032.1 |
Candille G, Talagrand O, 2008. Impact of observational error on the validation of ensemble prediction systems[J]. Q J R Meteor Soc, 134: 959-971. DOI:10.1002/qj.v134:633 |
Carlos Santos, Anna Ghelli, 2012. Observational probability method to assess ensemble precipitation forecasts[J]. Q J R Meteor Soc, 138: 209-221. DOI:10.1002/qj.v138.662 |
Ciach G J, Krajewski W K, 1999. Radar-rain gauge comparisons under observational uncertainties[J]. Appl Meteor, 38: 1519-1525. DOI:10.1175/1520-0450(1999)038<1519:RRGCUO>2.0.CO;2 |
Ferro C A, 2007. Comparing probabilistic forecasting systems with the brier score[J]. Wea Forecasting, 22(5): 1076-1088. DOI:10.1175/WAF1034.1 |
Gneiting T, Raftery A E, 2005. Weather forecasting with ensemble methods[J]. Science, 310(5746): 248-249. DOI:10.1126/science.1115255 |
Liang Li, Zhao Linna, Gong Yuanfa, et al, 2012. Probability distribution of summer daily precipitation in the Huaihe Basin of China based on Gamma distribution[J]. Acta Meteor Sin, 26(1): 72-84. DOI:10.1007/s13351-012-0107-2 |
Pappenberger F, Ghelli A, Buizza R, Bodis K, 2009. The skill of probabilistic precipitation forecasts under observational uncertainties within the generalized likelihood uncertainty estimation framework for hydrological applications[J]. Hydrometeorol, 10: 807-819. DOI:10.1175/2008JHM956.1 |
Roberts N M, Lean H W, 2008. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events[J]. Mon Wea Rev, 136: 78-97. DOI:10.1175/2007MWR2123.1 |
Saetra, Hersbach H, Bidlot J-R, Richardson D S, 2004. Effects of observation errors on the statistics for ensemble spread and reliability[J]. Mon Wea Rev, 132: 1487-1501. DOI:10.1175/1520-0493(2004)132<1487:EOOEOT>2.0.CO;2 |
Toth Z, Kalney E, 1993. Ensemble forecasting at NMC:the generation of perturbations[J]. Bull Amer Meteor Soc, 74(12): 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
Toth Z, Kalney E, 1997. Ensemble forecasting at NCEP and the breed method[J]. Mon Wea Rev, 125(12): 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2 |
Zhao Linna, Tian Fuyou, Wu Hao, et al, 2011. Verification and comparison of probabilistic precipitation forecasts using the TIGGE data in the upriver of Huaihe Basin[J]. Adv Geosci, 29: 95-102. DOI:10.5194/adgeo-29-95-2011 |
Zhao Linna, Qi Dan, Tian Fuyou, et al, 2012. Probabilistic flood prediction in the upper Huaihe catchment using TIGGE data[J]. Acta Meteor Sin, 26(1): 62-71. DOI:10.1007/s13351-012-0106-3 |
 2015, Vol. 41
2015, Vol. 41 