2. 美国国家海洋大气局国家环境预报中心, 华盛顿
2. NOAA/NCEP/Environmental Modeling Center, Washington, DC, U.S.A
20世纪90年代起,欧美等国先后建立了各自的全球中期集合预报业务系统,随后区域短期集合预报系统也于2001年在美国率先投入业务应用(Du et al,2001),集合预报产品开始逐步占据重要的位置,应用日趋广泛,已成为预报员中短期天气预报的重要参考产品(杨学胜,2001;杜钧等,2014a)。近年来,我国对集合数值预报日趋重视,国家气象中心分别建立了全球集合预报系统(GEPS)和区域集合预报系统(REPS)(邓国等,2010;Chen et al,2012),并在2008年北京奥运会期间成功组织了B08RDP项目,对多国中尺度集合预报系统开展了对比试验(Duan et al, 2012),进一步推动了我国集合预报技术的发展和应用。
与确定性预报一样,基于集合预报产品也发展了一些释用技术(魏凤英,1999;段明铿等,2006;马清等,2008;林春泽等,2009;邓国等,2010;陈朝平等,2010;李莉等,2011;陈法敬等,2011;陈良吕等,2014)。相对于确定性预报而言,集合预报不仅可以提供可能的预报误差分布和概率预报,并且集合平均预报通常比单个预报更准确(杜钧等,2010)。但在降水预报中,集合平均则并不总是比单个预报更准确(杜钧等,2014b),Du等(1997) 指出虽然平均后降水位置可能变得比较准确,但简单集合平均的平滑作用会造成小降水区扩张过大而大降水区缩减过小的问题。李俊等(2010a;2010b)在降水的集合预报试验和检验中也有类似结论。针对这一问题Ebert(2001a;2001b)提出了“概率或频率匹配”的思路(以下统称“频率匹配法”), 利用集合成员的原始降水频率来订正简单的算术集合平均降水预报得到所谓的“概率匹配集合平均”(probability-matched ensemble mean), 概率匹配集合平均既可保持经集合平均光滑后位置预报较准确的优点,同时又结合了原始集合成员在降水量级分布上较准确的优点。
本文基于“频率匹配法”的思路,根据参考频率的不同,分两种方法进行了集合降水预报的订正研究,一种方法是利用集合成员降水频率订正简单集合平均的平滑效应(以下简称“概率匹配平均”法),另一种方法是利用实况降水频率订正集合成员降水预报的系统偏差(以下简称“预报偏差订正”法)。上述两种方法的具体介绍和试验数据见第一节,在第二节利用北京2012年7月21日特大暴雨个例(李俊等,2015),分析了概率匹配平均法的效果及其在不同集合离散度情形下的差异(仅限集合平均预报)。在第三节利用武汉暴雨所的区域集合预报业务系统(李俊等, 2015),除通过批量试验进一步系统地检验概率匹配平均的效果外,还重点试验了上述两种订正方法相结合的综合效果,此外,还讨论了预报偏差订正对集合预报系统散离度和概率预报技巧的改进效果。
1 试验数据和方法由于分析概率匹配平均法和不同集合系统离散度关系的需要,在文中第二节用到北京2012年7月21日(“7.21”)特大暴雨个例的两组集合预报试验数据(李俊等,2015),每组试验21个成员;在文中第三节使用基于AREM短期集合预报系统2010年4月11日至7月31日逐日的集合降水预报资料,用批量试验分析概率匹配平均和预报偏差订正相结合对集合平均预报的改进效果, 同时也检验了预报偏差订正对集合离散度和概率预报等的影响。在偏差订正和降水检验中还用到全国2510个站点的逐日降水观测资料。
| $“频率匹配法”的基本思路是通过统计在不同等级阈值条件下降水出现的参考频率和预报频率(可以是空间上的或时间上的或二者兼用),把有偏差的预报频率调整到较准确的参考频率以保持两者在相同等级下降水频率的一致,从而达到订正降水偏差的方法(Ebert, 2001a;2001b;李俊等,2014;杜钧等,2014b)。本文的大部分计算基于全国2510个站点而不是模式格点。降水频率的计算方法如下:$ {{F}_{J}}=\frac{B_{J}^{{}}}{A} $ 式中,J表示自定义的不同等级降水阈值,FJ为降水阈值J的频率,A为总降水站次,BJ为降水阈值J出现的站次。$ | (1) |
基于上述“频率匹配法”的思路,根据参考频率的不同,文中采用了以下两种降水订正方法。
(1) 概率匹配平均
利用集合成员在某个阈值上的降水频率作为参考频率来订正简单算术平均集合降水预报。其中参考频率的BJ为某时次全体集合成员预报降水达到阈值J的总站次,A为全体集合成员预报的总站次。预报频率中BJ为该时次集合平均预报降水达到阈值J的总站次,A为集合平均预报的总站次。目的是去掉简单集合平均的平滑作用所造成的偏差。
(2) 降水预报的偏差订正
利用观测降水频率作为参考频率来订正预报。其中参考频率的BJ为前期实况降水达到阈值J的总站次,A为前期总降水站次,本文采用滑动平均的方法计算过去20 d观测各阈值降水的平均频率作为参考频率。预报频率计算方式与参考频率计算相似,为过去20 d内各集合成员或集合平均降水预报对应阈值的平均频率。目的是要消除由于模式系统(包括初、边值)缺陷造成的系统性偏差。李俊等(2014b)的分析表明,该方法能显著改善模式降水预报中雨量和雨区范围的系统性偏差,但对降水落区偏差的订正能力有限。本文侧重于将其与方案1结合,检验它们对集合降水预报改进的总体效果,以及对集合离散度和概率预报的订正效果。
在上述两种方案中,计算得到参考频率和预报频率后,均通过多项式插值的方法,得到不同阈值降水预报的订正系数,将这组阈值上的订正系数采取内插方式就可以得到任何降水量的订正系数,最后用该订正系数乘以对应站点的原始降水量预报值就得到订正后的降水量, 具体实施的技术方案可参阅李俊等(2014) 论文。
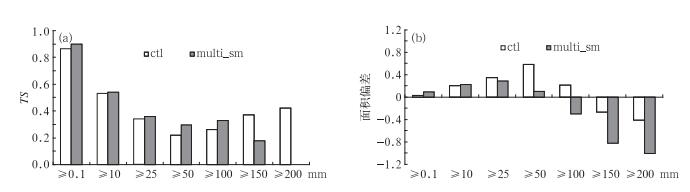
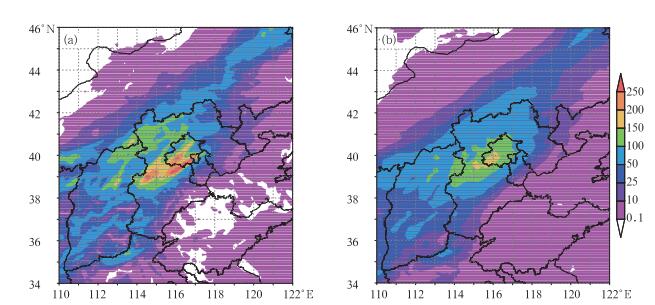
2 个例分析 2.1 概率匹配平均李俊等(2015) 基于WRF模式,分辨率9 km,采用6套扰动方案(初值、多物理、三组随机物理和初值与随机物理的混合)对2012年7月21日北京特大暴雨过程进行了集合降水预报试验,集合预报试验的起始时间为2012年7月20日00时(UTC,下同), 预报时效48 h,其中24~48 h预报时段与“7.21”暴雨过程对应。研究发现其中多物理方案组合的集合预报系统(multi)从总体来说效果最佳,较控制预报的改进最大,但是在大暴雨量级的集合平均预报multi_sm比控制预报ctl更差(图 1a),原因是集合平均的光滑作用使强降水区域大大地缩小了,这从降水区域面积偏差①的对比可以明显看到(图 1b)。集合平均(图 2b)同控制预报(图 2a)相比其强降水区(如>100 mm)大大缩小了,并且没有超过200 mm的降水区,而小雨区(如 < 10 mm)大大扩展了。
① 定义为AB=F/O-1,这儿F(O)为满足某一阈值的预报(观测)降水面积或格点或站点数,AB>,=,<0.0分別对应为湿、无和干偏差。
|
图 1 北京2012年“7.21”特大暴雨区域集合预定试验中,控制预报(ctl)、简单集合平均(multi_sm)24~48 h时段不同降水量级预报的(a)TS评分和(b)面积偏差 (检验范围为全中国2510个站点) Fig. 1 (a) Threat Scores (TS) and (b) area biases of the control member (ctl) and simple ensemble mean (multi_sm) over various rainfall thresholds for 24 h accumlated precipitation from 48 h forecasts, the result is based on the multi_physics ensemble in the Beijing 21 July 2012 torrential rain case in China(2510 stations) |
|
图 2 试验同图 1,(a)控制预报(ctl)和(b)简单集合平均(multi_sm)的24~48 h时段降水预报(单位:mm) Fig. 2 The same experiment as in Fig. 1, 24 h accumlated precipitation from the 48 h forecasts of (a) control member (ctl) and (b) simple ensemble mean (multi_sm) (unit: mm) |
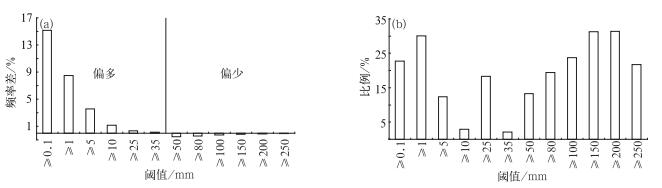
为了消除集合平均光滑所带来的负面作用,矫正简单算术平均在各阈值降水频率分布上的误差,采用第一节方案1,以Multi集合预报试验中21个成员各等级降水预报出现的频率作为参考频率,其集合平均预报对应等级降水出现的频率为预报频率。图 3a为预报频率和参考频率的差,总体而言,当阈值 < 50 mm时频率差 > 0,而50 mm以上降水的频率差 < 0,集合平均比原集合成员的小降水报得过多而强降水偏少。由于强降水区总是比弱降水区小很多,这使得强降水端的频率差看上去并不大, 但考虑到实况强降水区域也较小,这不大的频率差实际上却代表了相当一部分的实况降水区,这从相差的预报站点数(不同阈值集合平均降水站数与21个集合成员预报的平均站数的差)占实况出现站点数的比例就可看出(图 3b),如在降水超过150 mm的量级上的比值达到30%以上, 因此这部分降水频率的大调整对暴雨预报质量会有很大的影响。
|
图 3 试验同图 1,24~48 h时段不同阈值的降水预报中,(a)集合平均预报的频率与集合成员的平均频率的差,(b)集合平均降水站数与集合成员预报的平均站数的差值占实况站数的比例 Fig. 3 The same experiment as in Fig. 1, (a) frequency difference and (b) ratio of the difference in predicted station number to observed station number, between ensemble mean and members (averaged), over various rainfall thresholds for 24 h accumulated precipitation during the 24-48 h forecasing period |
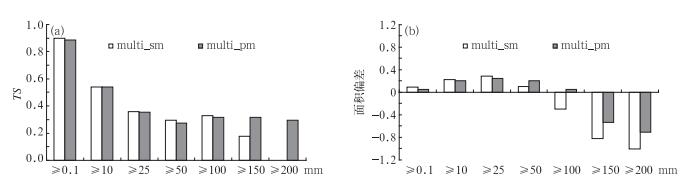
图 4a为简单平均(multi_sm)与概率匹配平均(multi_pm)降水TS评分的比较,虽然在 < 100 mm降水等级上的TS评分没有明显变化,但对 > 150 mm降水的TS评分有明显的改进,这是由于频率匹配通过调整降水量,增大了强降水的面积和强度,改进了原来150 mm以上降水大部分漏报的情况,因而TS评分得到明显改进。对应在降水面积偏差的变化上(图 4b), 与简单平均相比,在 < 50 mm量级的降水上,概率匹配平均的湿偏差减小,而在>100 mm量级的降水上,降水的干偏差减小,这一变化与图 3中对应等级的频率差一致,即频率匹配使得订正后的集合平均的小量级降水预报面积减小,而大量级降水面积增大。从图 5订正前后的集合平均降水预报也可直观地看到, 对比图 5a和5b,multi试验订正后0.1 mm以上的小雨区面积减小,而>100 mm的雨区面积增大,并且出现了>200和250 mm的强降水中心,与实况出现的位置接近(图略),即Multi试验的概率匹配平均降水预报,在雨区基本正确的基础上,降水强度预报得到了显著改善。
|
图 4 试验同图 1,简单集合平均(multi_sm)、概率匹配平均(multi_pm) 24~48 h时段降水预报对不同降水量级的(a)TS评分和(b)面积偏差 Fig. 4 The same experiment as in Fig. 1, (a) Threat Scores (TS) and (b) areas biases of the simple ensemble mean (multi_sm) and probability-matched mean (multi_pm) over various rainfall thresholds for 24 h accumulated precipitation during the 24-48 h forecasting period |
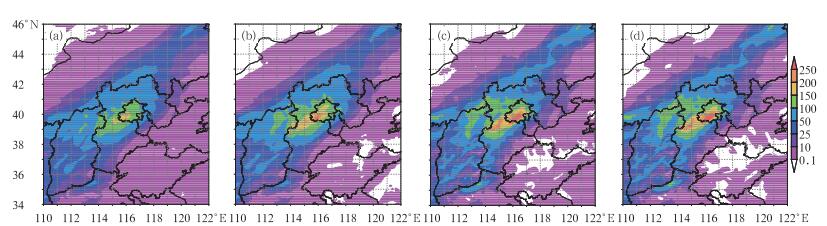
|
(a)简单集合平均(multi_sm)和(b)概率匹配平均(multi_pm)的24~48 h时段降水预报 (c, d与a, b相同,但对应随机物理过程集合预报试验kften, 单位: mm) he same experiment as in Fig. 1, 24 h accumulated precipitation from the 48 h forecasts of (a) simple ensemble mean (multi_sm) and (b) probability-matched mean (multi_pm) (Figs. 5c and 5d are the same as Figs. 5a and 5b but for the stochastic physics ensemble kften, unit: mm) |
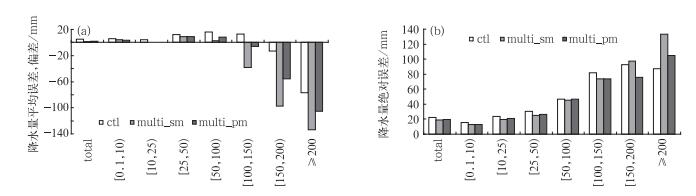
虽然概率匹配平均可以通过缩减弱降水区和扩展强降水区来提高不同量级降水预报范围和量的准确性,但由于这种调节在大小降水两端恰好相反,因此概率匹配平均对于整个预报区域内的总降水量调节作用是有限的,并且这种调节是基于集合成员的降水频率,即把简单集合平均在各量级上的降水调回到原集合成员的水平,因此概率匹配平均应该仍具有集合成员原有的系统性偏差。图 6可以说明这一点, 图 6a和6b分别为平均误差(降水量的偏差)和绝对误差。从总降水量来看,两种集合平均方法,均可较控制预报减小总降水量预报的误差特别是平均误差, 但比较两种平均预报,无论是平均误差(图 6a)还是绝对误差(图 6b),概率匹配平均(multi_pm)较简单平均(multi_sm)均无改进,系统性的降水量偏多仍然存在;从分量级的降水误差来看,总体而言,概率匹配平均有把简单平均拉回到控制预报的趋势,所以对于强降水端的大暴雨预报,在平均误差和绝对误差上它较简单平均的改进还是非常显著的。由此可见,用集合成员订正集合平均预报,尽管可以改进降水在各个量级上的分配,避免小降水报得过多而强降水报得过少的现象,尤其是对强降水负面影响的订正(这一点对暴雨集合预报更加重要),但却没有能力改进降水量的系统性偏差。降水量的系统性偏差往往是由于模式系统缺陷造成的,而单纯使用概率匹配平均对此无能为力,但可以通过降水量偏差订正得到改善(见3.2节)。
|
图 6 试验同图 1,控制预报(ctl)、简单集合平均(multi_sm)、概率匹配平均(multi_pm) 24~48 h时段降水预报的总体和分级的(a)平均误差(即雨量偏差)和(b)绝对误差(单位: mm) Fig. 6 The same experiment as in Fig. 1, (a) mean errors (rainfall amount bias) and (b) absolute errors of the control member (ctl), simple ensemble mean (multi_sm) and probability-matched mean (multi_pm) over the total and various categories of precipitation amount for 24 h accumulated precipitation from the 48 h forecasts (unit: mm) |
概率匹配平均基于集合成员的降水频率,因而其作用应该同集合预报系统的离散度有关。当集合离散度越大,集合平均的光滑作用就愈明显,相应参考频率和预报频率的差异也越大,则订正效果应该越明显;反之,作用愈小,当离散度为零时,就没有订正作用。在李俊等(2015) 的试验中, 随机扰动物理方案(kften)的集合离散度最小,远远小于多物理过程组合方案(multi)(图 7),以下通过这两组方案的比较,来分析离散度对概率匹配平均结果的影响。图 8为两组试验平均降水预报订正前后TS评分的差值和偏差的差值,如图,kften集合平均的TS评分(图 8a)和降水面积偏差(图 8b)在用概率匹配平均方法订正前后没有什么改变,在强降水端概率匹配平均较简单平均的改进程度都远小于multi集合系统。比较图 5c和5d也可直观地看到kften试验中订正前后的平均降水预报变化不大(这同图 5a到5b的明显变化截然不同)。通常一个好的集合预报系统有较大的离散度,因而更有必要使用概率匹配方法来修正其集合平均预报(从图 5a订正到图 5b)。
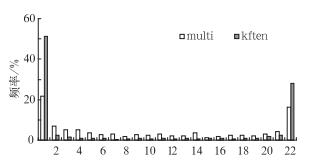
|
图 7 试验同图 1,多物理过程multi和随机物理过程kften集合预报试验24~48 h时段降水预报的Talagrand分布 Fig. 7 The same experiment as in Fig. 1, Talagrand distributions of the multi-physics (multi) and stochastic physics (kften) ensembles for 24 h accumulated precipitation from the 48h forecasts |
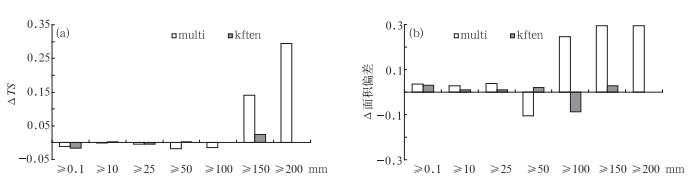
|
图 8 试验同图 1,multi和kften集合预报试验中,概率匹配平均不同量级降水预报相对简单集合平均的改进 (a) TS评分的差值, (b)面积偏差的差值 Fig. 8 The same experiment as in Fig. 1, forecast improvements of probability-matched mean over simple ensemble mean over various rainfall thresholds in terms of the differences in (a) Threat Score (TS) and (b) areal bias for the multi-physics (multi) and stochastic physics (kften) ensembles |
在个例试验的基础上,以下用业务预报系统进行批量试验,一方面用批量试验进一步验证概率匹配平均的效果,另一方面分析预报偏差订正对集合预报系统散离度和概率预报技巧的改进效果以及两种方案结合的综合效果。批量试验基于武汉暴雨研究所的AREM短期集合预报系统(AREM_EPS)(李俊等,2010a),该系统采用AREM模式(宇如聪等,2004) 并行版本,考虑了模式初值和侧边界的不确定性,初值扰动采用增长模繁殖法BGM(Breeding of Growing Mode)(Toth et al, 1993;1997;李俊等,2009),侧边界采用随机扰动方案,含控制预报在内共11个成员,预报范围为5°~60°N、65°~145°E,模式分辨率为37 km。
概率匹配批量订正试验从2010年5月1日至7月31日(92 d)三个月逐日滚动,用当日全体集合成员的频率分布订正其简单集合平均。降水预报偏差订正时段与概率匹配试验一致,但在开始时段用到了4月11—30日的资料,统计过去20 d滑动平均的观测和预报的降水频率。考虑到文章篇幅和结论相似,下文仅给出批量试验中24~48 h的结果和分析。
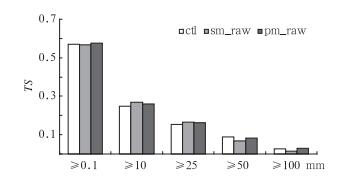
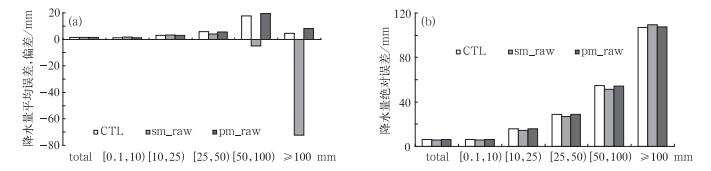
3.1 概率匹配平均采用第1节方案1,对逐日的简单集合平均降水进行概率匹配订正,总体而言,概率匹配平均批量试验结果与第2节个例分析结果一致。图 9为三个月降水的TS评分,对于弱降水(≥0.1 mm)和强降水(≥100 mm)两端的降水落区, 概率匹配平均(pm_raw)较简单平均(sm_raw)都有改善,尤其在暴雨和大暴雨降水端;图 10显示, 概率匹配平均对各量级的降水量预报有使简单平均回归到控制预报的趋势,在大暴雨量级上平均误差远远小于简单平均预报,绝对误差也有所改善,但在其他较小降水量级上和对总雨量预报误差却没有改善(甚至使绝对误差略有増加)。所以,虽然利用集合成员可以有效地订正由于集合平均光滑作用所造成的雨区面积伸缩或降水量重新分配的问题,但却无法订正由于模式系统误差所造成的雨量的系统误差,以下结合第一节提到的方案2(预报偏差订正),用过去的观测降水来订正预报的系统偏差。此法对单一预报的订正效果已有详细分析(李俊等,2014),本文重点分析它对集合离散度和概率预报的订正效果以及同概率匹配集合平均相结合的总效果。
|
图 9 2010年5月1至7月31日AREM区域集合预报的控制预报(ctl)、简单平均(sm_rsw)、概率匹配平均(pm_raw) 24~48 h时段不同量级降水预报的TS评分 Fig. 9 Threat Scores (TS) of the control member (ctl), simple ensemble meam (sm_raw) and probability-matched mean (pm_raw) over rainfall thresholds for 24 h accumulated precipitation from the 48 h forecasts. The result is based on the precipitation forecasts of a regional ensemble prediction system based on AREM during the period from May 1 to July 31 2010 |
|
图 10 试验同图 9,24~48 h时段控制预报(ctl)、简单集合平均(sm_raw)、概率匹配平均(pm_raw)降水量预报总体和分级的,(a)平均误差和(b)绝对误差(单位: mm) Fig. 10 The same experiment as in Fig. 9, (a) mean errors and (b) absolute errors of the control members (ctl), simple ensemble mean (sm_raw) and probability-matched mean (pm_raw) over the total and various categories of precipitation amount for 24 h accumulated precipitation from the 48 h forecasts (unit: mm) |
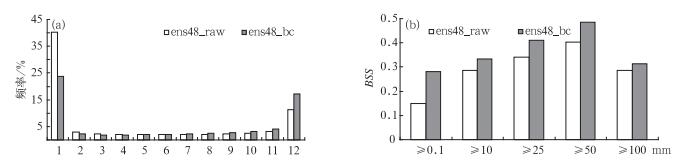
采用第一节方案2,用观测降水对11个集合成员分别进行了降水偏差订正,共统计了0.1、1、5、10、25、35、50、80、100和150 mm 10个阈值的参考和预报频率。集合预报的一个主要目的是给出预报的可信度和预报误差的分布,这通常用离散度来表达,而概率预报包含了一个集合系统所能提供的所有信息,因此通常用离散度和概率预报的质量来衡量集合预报系统的性能。图 11a为常用来描述集合离散度的Talagrand分布或分级直方图(Talagrand et al,1997;杜钧,2002)。如图 11所示,订正前24~48 h降水预报(ens48_raw)的Talagrand分布指出实况落在集合预报区间下限以外的频次远高于其他区间,呈“L”型,表明降水离散度偏小并具有系统性湿偏差。这主要是由于AREM模式预报小雨面积过大的原因,从实况参考频率和各集合成员预报频率的对比看(图略),绝大多数量级上预报频率大于参考频率,并且5 mm以下降水的频率差异更显著,这与Chen等(2013)和李俊等(2014) 分析的AREM模式降水系统偏差特征一致。
|
图 11 试验同图 9,(a)利用实况订正集合成员24~48 h时段降水偏差前(ens48_raw)和后(ens48_bc)的Talagrand分布;(b)和(a)同,但为概率预报的BRIER技巧评分 Fig. 11 The same experiment as in Fig. 9, (a) Talagrand distributions of 24 h accumulated ensemble precipitation from the 48 h forecasts with (ens48_bc) and without (ens48_raw) bias correction; (b) is the same as (a) but for Brier skill Score (BSS) of probabilistic forecasts |
订正后24~48 h降水预报(ens48_bc)的Talagrand分布明显得到改善,系统性湿偏差得到修订(区间1的频次明显降低),分布从L型变为U型, 集合离散度质量(方向)得到改善。由于对集合成员预报量本身的偏差订正一般只能导致集合预报分布的中心(平均)位置的位移,而并不能较大地改变分布的形状和区间范围的大小,所以一般并不改进集合离散度大小(相反,由于订正后集合成员变得较准确而互相靠近, 这往往会导致离散度减小),因此在区间1(小于集合预报区间下限)的频次减小的同时,区间12的频次也增加了,即实况落在集合预报区间上限之外的几率增加了;在AREM模式降水预报有系统性湿偏差的背景下,具体表现在偏差订正后,尽管对弱降水空报减少,但也导致对强降水漏报率的增加。反之,如果模式有干偏差,则订正后应表现为空报增加,而漏报减少。
离散度质量的改进(这里主要是方向的改进)必然会使基于该集合的概率预报包含更多的信息量或可预报性增加,我们采用Brier技巧评分(BSS)方法,对订正前后降水预报的概率技巧进行了检验,具体计算方法见附录。图 11b为订正前后降水预报的BSS,经过订正,24~48 h降水预报的概率技巧均有明显提高;总体而言,偏差订正后AREM模式集合预报系统无论对小雨、中雨、大雨,还是暴雨和大暴雨都有较强的概率预报能力, 对25和50 mm以上的雨区效果尤佳。
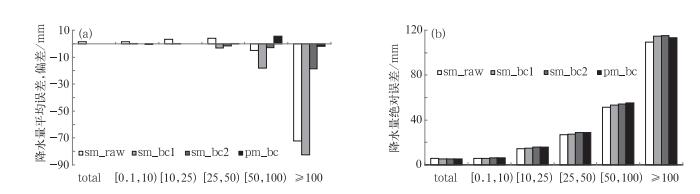
图 12a和12b为92 d平均的、预报偏差订正前后集合平均降水量预报的平均误差和绝对误差, sm_raw为未经订正的原始集合成员的简单平均,sm_bc1,sm_bc2同样采用实况频率订正降水偏差,其中sm_bc1为11个集合成员偏差订正后的简单算术平均,sm_bc2为对原始集合成员的简单平均(sm_raw)直接用实况订正。如图,对总降水量而言, 订正前sm_raw的平均误差明显大于0时mm,表明集合预报系统存在系统性的湿偏差(与图 10一致), 两种偏差订正方案(sm_bc1和sm_bc2) 订正后的集合平均降水量的平均误差均大大减小且系统性的湿偏差得到修正(几乎在0 mm附近),其中直接对平均预报进行订正(sm_bc2) 的效果略好, sm_bc2较sm_bc1的优越性在分量级的降水预报中更明显,如图 12a显示在大雨、暴雨和大暴雨中sm_bc2的平均偏差大大小于sm_bc1;图 12b显示,对整个预报区域内的总降水量而言,平均预报的绝对误差也略有改善,其绝对误差均小于订正前, 但在分量级的降水预报中改善不明显,一个可能的原因是雨区的预报位置同实况有较大差异,虽然通过订正同量级降水范围接近了,但位置的偏差使站点对站点的预报误差不减甚至反增, 可见降水量偏差的订正效果还取决于一个模式对降水落区的预报能力。
|
图 12 试验同图 9,24~48 h时段不同集合平均算法下降水预报总体和分级的(a)平均误差和(b)绝对误差(单位: mm) [sm_raw (sm_bcl)为集合成员预报偏差订正前(后)的简单集合平均,sm_bc2为直接对sm_raw进行预报偏差订正的结果,pm_bc为预报偏差订正后集合成员的概率匹配平均] Fig. 12 The same experiment as in Fig. 9, (a) mean errors and (b) absolute errors of the different ensemble mean during the 24-48 h forecasting period for the total and various categories of precipitation amount [sm_raw (sm_bcl) refers to simple ensemble mean derived from raw (bias-corrected) individual members, sm_bc2 refers to the forecast directly removing bias from sm_raw, and pm_bc refers to probability-matched mean on bias-corrected individual members (unit: mm)] |
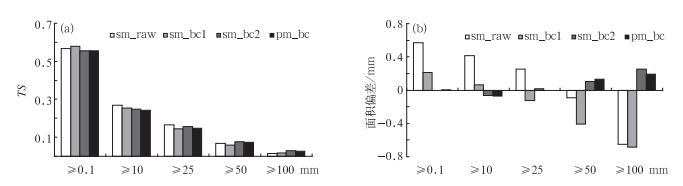
图 13a为相应的集合平均降水落区预报的TS评分在订正前后的变化, 除暴雨以上量级外,二种方案(sm_bc1和sm_bc2) 偏差订正对落区预报(TS评分)改进都不大或略差。以上结果同我们前期工作(李俊等,2014) 的结论是一致的, 即采用实况频率对降水预报进行订正,可以较大地改进降水量的预报效果但对落区预报(TS评分)改进不大。值得注意的是直接订正平均预报(sm_bc2) 要优于11个集合成员偏差订正后的简单算术平均(sm_bc1),尤其是暴雨和大暴雨降水落区预报(TS评分),这一结果同图 13b中所示的雨区面积偏差的变化结果相一致。从图 13b看到,与sm_bc1比较,sm_bc2订正方案可更有效地订正各降水量级的降水面积偏差,特别是对暴雨和大暴雨量级;这因为尽管sm_bc1每个成员的系统偏差得到了订正,但随后的简单平均又使强降水区被大大地缩小了(造成或加强干偏差),而sm_bc2方案是直接针对集合平均预报本身用实况订正,同时消除了集合成员带来的系统偏差和简单平均带来的量级分布偏差。
|
图 13 试验同图 9,24~48 h时段不同集合平均预报的(a)TS评分和(b)面积偏差 (具体图例说明同图 12) Fig. 13 he same experiment as in Fig. 9, (a) Threat Scores (TS) and areal biases of the different ensemble mean during the 24-48 h forecasting period over various rainfall thresholds (The four mean forecasts are the same as that described in Fig. 12) |
对于未经订正的原始集合预报,前面分析表明概率匹配集合平均可以改善两端降水的落区预报,尤其是在强降水的TS评分上较简单平均有较大的改进, 那么对于已经过预报偏差订正后较准确的集合预报是否也有同样的改进效果呢?下面用订正过的集合成员进行研究,以降水偏差订正后的11个集合成员的降水频率作为参考频率,对基于订正后成员的简单平均降水进行概率匹配订正(pm_bc),希望可以在集合平均降水预报系统性偏差得到订正的基础上,进一步使预报在各量级上的分布更加合理。结果见图 12和图 13,比较sm_bc1和pm_bc,它们分別代表简单平均和概率匹配平均:对于降水量预报的平均误差(图 12a),在总降水量以及小雨和大雨等级上两者差别不大,而在大雨到大暴雨的量级上概率匹配平均明显优于简单平均,在绝对误差上(图 12b)两者差别也不大;对于降水落区和范围(图 13),概率匹配平均较简单平均也有明显改进,如图 13a显示对暴雨和大暴雨量级,pm_bc的TS评分均高于sm_bc1的TS评分,图 13b显示概率匹配订正前的集合平均(sm_bc1) 在各降水量级都有或湿或干的偏差, 但概率匹配集合平均降水预报(pm_bc)的偏差几乎都小于sm_bc1,除50和100 mm量级有湿偏差外,其他量级的面积偏差均接近为零(无偏差), 而在50和100 mm量级上,pm_bc的面积偏差大大地小于sm_bc1。由上可见, 即使当每个集合成员降水预报先进行了偏差订正后,概率匹配平均仍可明显地改善简单集合平均。
因此,在最终的集合平均计算中,可以综合采用第一节这两种订正方法(以实况为参考频率和以集合成员预报为参考频率),采取两步订正(订正预报系统偏差和订正集合平均光滑负作用),获得既能消除降水量的系统性偏差同时各量级降水分布又合理的集合平均预报。这两种方法互为补充,偏差订正可以大大地消除降水量预报的系统误差,而概率匹配平均可以在一定程度上校正降水落区(通过平均过程)和不同量级范围(通过频率匹配)的误差,所以两者结合可以达到较佳的预报结果(李俊等,2014)。最后值得注意的是,比较sm_bc2和pm_bc,可见对集合平均预报直接进行偏差订正的效果(sm_bc2) 同综合订正效果(pm_bc)大致相当,这是因为sm_bc2方案是直接对集合平均预报进行偏差订正,所以由平滑造成的那部分偏差信息已包含在统计的结果中而“顺便”被订正了,它同时包含了对预报系统偏差的订正和对集合平均光滑负作用的订正, 其长期平均作用应该同两步综合订正相似(但pm_bc方法也许在较极端事件的个例中会更合适),因此,对降水集合平均的这两种处理方案(pm_bc或sm_bc2) 都可以在业务集合降水预报中采用。
4 结论和讨论本文基于“频率匹配法”的基本思路,采用基于集合成员频率的“概率匹配平均”和基于实况降水频率的“预报偏差订正”的两种订正方法,通过个例和批量试验,进行了集合降水预报的误差订正研究,结果表明:
(1) 采用集合成员频率订正后的集合平均降水预报,可以改进简单平均中平滑造成的小量级降水增多而强降水被削弱的现象,概率匹配平均对简单平均的改进主要表现在对不同量级降水范围的调整上,尤其是强降水的范围,而对整个区域的总降水量预报没有改进;当集合预报系统离散度愈大时这种订正效果也愈好。
(2) 概率匹配集合平均不能订正由于模式系统缺陷所导致的系统性误差,这种系统性的预报偏差可以利用过去的实况来加以订正。研究结果表明,采用预报偏差订正方法,可以明显订正降水量和雨区范围的系统性误差, 但对落区预报的改进有限;对集合成员进行偏差订正也能明显地改进集合预报系统的离散度特征和概率预报技巧;对于集合平均预报需要单独进行偏差订正, 这样做的效果要优于单个成员偏差订正后的简单算术平均。
(3) 综合采用以上两种订正方法,可以获得既能消除系统性偏差同时各量级降水分布又合理的集合平均降水预报。结果表明,即使在预报系统性偏差被订正后, 概率匹配平均较简单平均在暴雨和大暴雨量级仍有明显的改进,其原因是偏差订正可以大大地消除降水量预报的误差,而概率匹配平均可以在一定程度上校正降水落区(通过平均过程)和不同量级范围(通过频率匹配)的误差,所以这两种方法互为补充,它们的结合既改进降水量的预报也可以改进降水落区和范围的预报,达到较佳的预报结果,因此,在实际业务中可以综合使用上述两种方法处理集合平均降水预报。
本文涉及到两个模式,在个例分析中使用的是WRF模式个例试验的结果,在批量试验中使用的是中国气象局武汉暴雨研究所AREM短期集合预报系统,是互相独立的资料,尽管其系统的偏差特性不同, 但也进一步说明了“频率匹配”原理的普适性, 该方法对具有不同系统偏差的系统同样适用,通过订正可以减小原来的偏差(无论是干偏差或湿偏差)。
附录Brier评分和Brier技巧评分
Brier评分(Brier Score, BS) (Brier, 1950;Murphy, 1973) 常用来检验概率预报的好坏,它类似用于单一预报评分的均方差,但这里不用预报量而用某一事件(如降水≥100 mm)的预报概率, 见式(1):
| $ BS=\frac{1}{N}\sum\limits_{i=1}^{n}{{{(Fst_{pro}^{i}-Obs_{pro}^{i})}^{2}}} $ | (1) |
式中,i=1, 2, 3, …, N表示N个站点,Fstxpro表示预报出现某个阈值事件的概率,Obspro表示实况出现该阈值事件的概率,当实况出现时Obspro=1,实况不出现时Obspro=0。相应地,Brier技巧评分(Brier Skill Score, BSS)可以定义如下(李俊等, 2010b):
| $ BSS=\frac{B{{S}_{\text{ref}}}-B{{S}_{\text{fst}}}}{B{{S}_{\text{ref}}}-B{{S}_{\text{per}}}} $ | (2) |
式中,BSref表示参考预报的BS评分,BSfst表示集合概率预报的BS评分,BSper表示完美概率预报的BS评分。由式(1) 可见当BS=0时,概率预报效果最好,即所谓完美预报;此外,本文检验以订正前的控制成员(ctl)作为参考预报,因此式(2) 可简化为:
| $ BSS=\frac{B{{S}_{\text{ctl}}}-B{{S}_{\text{fst}}}}{B{{S}_{\text{ctl}}}} $ | (3) |
类似于实况,单一控制预报的概率也是非1即0。
陈朝平, 冯汉中, 陈静, 2010. 基于贝叶斯方法的四川暴雨集合概率预报产品释用[J]. 气象, 36(5): 32-39. DOI:10.7519/j.issn.1000-0526.2010.05.004 |
陈法敬, 矫梅燕, 陈静, 2011. 一种温度集合预报产品释用方法的初步研究[J]. 气象, 37(1): 14-20. DOI:10.7519/j.issn.1000-0526.2011.01.002 |
陈良吕, 陈静, 陈德辉, 等, 2014. 基于T213集合预报的延伸期产品释用方法及初步检验[J]. 气象, 40(11): 1293-1301. DOI:10.7519/j.issn.1000-0526.2014.11.001 |
邓国, 龚建东, 邓莲堂, 等, 2010. 国家级区域集合预报系统研发和性能检验[J]. 应用气象学报, 21(5): 513-523. DOI:10.11898/1001-7313.20100501 |
杜钧, 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28. |
杜钧, 陈静, 2010. 单一值预报向概率预报转变的基础:谈谈集合预报及其带来的变革[J]. 气象, 36(11): 1-11. DOI:10.7519/j.issn.1000-0526.2010.11.001 |
杜钧, 康志明, 2014a. 天气预报中不确定性问题的调查分析[J]. 气象科技进展, 4(1): 58-67. |
杜钧, 李俊, 2014b. 集合预报方法在暴雨研究和预报中的应用[J]. 气象科技进展, 4(5): 6-20. |
段明铿, 王盘兴, 2006. 一种新的集合预报权重平均方法[J]. 应用气象学报, 17(4): 488-493. DOI:10.11898/1001-7313.20060416 |
李俊, 杜钧, 陈超君, 2014. 降水偏差订正的频率(或面积)匹配方法介绍和分析[J]. 气象, 40(5): 580-588. DOI:10.7519/j.issn.1000-0526.2014.05.008 |
李俊, 杜钧, 刘羽, 2015. 北京"7[J]. 21"特大暴雨不同集合预报方案的对比试验.气象学报, 73(1): 50-71. |
李俊, 杜钧, 王明欢, 等, 2009. 中尺度暴雨集合预报系统研发中的初值扰动试验[J]. 高原气象, 28(6): 1365-1375. |
李俊, 杜钧, 王明欢, 等, 2010a. AREM模式两种初值扰动方案的集合降水预报试验及检验[J]. 热带气象学报, 26(6): 217-228. |
李俊, 王明欢, 公颖, 等, 2010b. AREM短期集合预报系统及其降水预报检验[J]. 暴雨灾害, 29(1): 30-37. |
李莉, 李应林, 田华, 等, 2011. T213全球集合预报系统性误差订正研究[J]. 气象, 37(1): 31-38. DOI:10.7519/j.issn.1000-0526.2011.01.004 |
林春泽, 智协飞, 韩艳, 等, 2009. 基于TIGGE资料的地面气温多模式超级集合预报[J]. 应用气象学报, 20(6): 706-712. DOI:10.11898/1001-7313.20090608 |
马清, 龚建东, 李莉, 等, 2008. 超级集合预报的误差订正与集成研究[J]. 气象, 34(3): 42-48. DOI:10.7519/j.issn.1000-0526.2008.03.007 |
魏凤英, 1999. 全国夏季降水区域动态权重集成预报试验[J]. 应用气象学报, 10(4): 402-409. |
杨学胜, 2001. 业务集合预报系统的现状及展望[J]. 气象, 27(6): 3-9. DOI:10.7519/j.issn.1000-0526.2001.06.001 |
宇如聪, 薛纪善, 徐幼平, 2004. AREMS中尺度暴雨数值预报模式系统[M]. 北京: 气象出版社, 3-7.
|
Brier G W, 1950. Verification of forecasts expressed in terms of probability[J]. Mon Wea Rev, 78: 1-3. DOI:10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2 |
Chen Jing, Tian Hua, Guo Deng, et al. 2012. The global ensemble prediction system (GEPS) and regional ensemble prediction system (REPS) at CMA and its application in monsoon season. 92nd American Meteorological Society Annual Meeting, January 22-26, New Orleans, LA.
|
Chen Jing, Wang Yu, Li Li, et al, 2013. A unified verification system for operational models from Regional Meteorological Centres of China Meteorological Administration[J]. Meteor Appl, 20: 140-149. DOI:10.1002/met.2013.20.issue-2 |
Du Jun, Steven L M, Frederick Sanders, 1997. Short-range ensemble forecasting of quantitative precipitation[J]. Mon Wea Rev, 125: 2427-2459. DOI:10.1175/1520-0493(1997)125<2427:SREFOQ>2.0.CO;2 |
Du Jun, Steve T, 2001. Implementation of a real-time short-range ensemble forecasting system at NCEP: An update[J]. Preprints, 9: 355-356. |
Duan Yihong, Gong Jiandong, Du Jun, et al, 2012. An overview of the Beijing 2008 Olympics Research and Development Project (B08RDP)[J]. Bull Amer Meteor Soc, 93: 381-403. DOI:10.1175/BAMS-D-11-00115.1 |
Ebert E E, 2001a. Ability of a poor man's ensemble to predict the probability and distribution of precipitation[J]. Mon Wea Rev, 129: 2461-2479. DOI:10.1175/1520-0493(2001)129<2461:AOAPMS>2.0.CO;2 |
Ebert E E. 2001b. Probability-matched ensemble mean. Available online at http://www.cawcr.gov.au/staff/eee/etrap/probmatch.html.http://www.cawcr.gov.au/staff/eee/etrap/probmatch.html
|
Murphy A H, 1973. A new vector partition of the probability score[J]. J Appl Meteor, 12(4): 595-600. DOI:10.1175/1520-0450(1973)012<0595:ANVPOT>2.0.CO;2 |
Toth Zoltan, Kalnay E, 1993. Ensemble forecasting at NMC: The generation of perturbations[J]. Bull Amer Meteor Soc, 74: 2317-2330. DOI:10.1175/1520-0477(1993)074<2317:EFANTG>2.0.CO;2 |
Toth Zoltan, Kalnay E, 1997. Ensemble forecasting at NCEP and the breeding method[J]. Mon Wea Rev, 125: 3297-3319. DOI:10.1175/1520-0493(1997)125<3297:EFANAT>2.0.CO;2 |
Talagrand O, Vautard R, 1997. Evaluation of probabilistic prediction system[J]. Workshop on Predictability ECMWF, 10: 20-22. |
 2015, Vol. 41
2015, Vol. 41 