引言

重庆地处中亚热带西部，主城区座落在长江与嘉陵江汇合处，两江环抱，依山建城，公路蜿蜒曲折，上下盘旋，是典型的山城，包括渝中区、江北区、渝北区、南岸区、九龙坡区、大渡口区、沙坪坝区、北碚区和巴南区共9个区，面积5468.7 km²。重庆主城区属东亚内陆季风区，夏季受西南夏季风影响，高温、多雨、是我国暴雨频发的大城市之一。

重庆市现行的暴雨强度公式为87版公式，其推导数据只有8年，且为1973年之前的基础资料；在过去二十多年的使用中，有效地指导了城市雨水排水规划设计工作，在城市雨水灾害防治管理、预警和应急处置及城市建设等方面起到了重要的作用。在全球变暖的大背景下，虽然不同地区有所差异，但极端强降水的频率和强度整体呈增大趋势，给城市市政排水带来了更大的潜在压力(任雨等，2012)。如2007年“7·17”强降水事件(王中等，2008；宗志平，2007)，造成重庆市沙坪坝区陈家桥镇城市排水不及，积涝严重，交通、电力、通信、供水、供气一度中断，上万名群众被困，造成了严重的社会影响和经济损失。2009年8月4日，暴雨袭击重庆，重庆主城主干道不少路段积水严重，山城变泽国；千年古镇磁器口临江房屋已快被江水没顶，当地居民只能乘船来往通行。在气候变化和城市化快速发展背景下，现行暴雨强度公式在准确性、适用性等方面出现了不足。为了应对气候变化和经济社会发展需求，做好城市暴雨内涝防御工作，提高城市排水规划及工程设计的科学性，利用最新的雨量资料对暴雨强度公式进行推算显得尤为迫切。

邱兆富等(1999)、罗雅文(2012)和金超(2012)对重庆主城区的暴雨强度公式进行了推算，由于仅对沙坪坝站进行了研究，降水的地区差异被忽视，所得暴雨强度公式难以完全适应重庆主城区市政建设的需要。因此，有必要采用重庆主城区4个国家气象站最新的降水资料推算暴雨强度公式，分析降水量空间差异特征，探讨暴雨强度公式的适用范围，这将为重庆市主城区雨水排水系统的规划、设计和管理提供重要依据。

1 数据与方法 1.1 数据

重庆市气候中心根据中国气象局组织编制的“降水自记纸彩色扫描数字化处理系统”，对重庆市沙坪坝(57516)、北碚(57511)、渝北(57513)、巴南(57518) 等国家气象站的自记降水纸资料进行了数字化处理，形成了4站1981—2013年逐年逐分钟降水序列。在资料使用前对原始数据进行了质量检查、审核与一致性分析，4站数据完整率均为100%。

1.2 方法

暴雨取样方法：水文统计学的取样方法有年最大值法和非年最大值法两类，现行《室外排水设计规范》(2014年版；下称现行规范)(中华人民共和国住房和城乡建设部，2014)规定具有20年以上自动雨量记录的地区，排水系统设计暴雨强度公式应采用年最大值法。由于短历时强降水作为随机变量具有一定的不确定性，超过城市雨水排除系统设计标准的短时强降水，有的年份可能出现多次，有的年份可能一次也不会出现，年最大值法每年取一个最大值会遗漏一些数值较大的暴雨，丢掉一些有用信息(徐连军等，2007)。本研究采用年最大值法与年多个样法两种方法，年多个样法是非年最大值法中的一种，在城市暴雨强度公式编制中应用较为广泛(任雨等，2012)。

年最大值法是5、10、15、20、30、45、60、90、120、150、180 min(下称各历时)每年各选一个最大值。年多个样法是每年每个历时挑选前8个最大值，将选出的资料按从大到小排列(各历时分别进行)，取前n组数据(年数4倍)。按上述方法，分别建立沙坪坝、渝北、巴南和北碚站1981—2013、1991—2013年年最大值法、年多个样法的暴雨采样基本数据。

在使用年最大值法推算过程中，会出现大雨年的次大值大于小雨年的最大值而不被入选的情况，该方法算得的暴雨强度小于年多个样法的计算值，因此采用年最大值法时需作重现期修正，根据文献(Chow，1964；金家明，2010)方法，对年最大值法与年多个样法之间的对应重现期进行转换。

概率分布拟合：采用耿贝尔分布(邵尧明等，2008)、指数分布(邓培德，1996；2006)、皮尔逊Ⅲ型(顾骏强等，2000)概率分布拟合。

现行规范给出的暴雨强度公式形式为：

$q = \frac{{167{A_1}(1 + c{\rm{lg}}P)}}{{{{\left( {t + b} \right)}^n}}}$

(1)

式中，q为暴雨强度(单位：L·s^-1·hm^-2)，P为重现期(单位：a)，t为降雨历时(单位：min)，A₁、b、c、n为需求的参数。

2 暴雨强度公式推算 2.1 暴雨强度公式及误差

暴雨强度公式推算，在许多文献(植石群等，2000；邵尧明等，2008；余连荣等，2011)已有详细介绍，主要步骤有：(1) 对选取的各历时降雨资料，采用耿贝尔分布、指数分布、皮尔逊Ⅲ型概率分布拟合加以调整，得出降水强度、重现期、降水历时(i-P-t)的关系值。(2) 根据i-P-t关系值，采用最小二乘法(植石群等，2000)求解A₁、b、c、n各个参数，将求得的各参数代入式(1) 中，即得该站的暴雨强度公式。(3) 为确保计算结果的准确性，采用平均绝对均方误差和平均相对均方误差对暴雨强度计算结果进行精度检验(任雨等，2012)。

顾骏强等(2000)认为某个概率分布拟合对暴雨强度样本拟合的精度高，其对应的暴雨强度公式拟合的精度不一定也相应高。任恒钦等(2009)研究指出多数情况下单一重现期公式更接近拟合实测值，但应用不方便，对于个别情况如城市大型或重要的雨水泵站、排水泵站等，可考虑采用单一重现期公式；如暴雨强度总公式精度高，达到规范精度要求，在实际应用中更具指导意义。因此，沙坪坝站给出由不同年限资料、不同选样方法和不同概率分布拟合的暴雨强度总公式及误差分析值(表 1)。

由表 1可见，沙坪坝站利用近30 a两时段资料，采用年最大值法、年多个样法选样，利用指数分布、皮尔逊Ⅲ型、耿贝尔分布曲线拟合得到的暴雨强度公式均通过精度检验，指数分布曲线平均绝对均方差与平均相对均方差最小，分别为0.032 mm·min^-1和2.40%(1981—2013年多个样法选样)、0.027 mm·min^-1和1.97%(1991—2013年多个样法选样)。这与顾骏强等(2000)对概率分布拟合对比分析的结论相一致。值得注意的是，年多个样法不同概率分布拟合的精度均高于年最大值法。

由于暴雨强度公式数学表达式的参数均为拟合值，在计算过程中难免存在一定的误差，平均绝对均方差与平均相对均方差最小时才是最优解(任恒钦等，2009)。由于篇幅所限，渝北、巴南、北碚站仅列出1981—2013、1991—2013年两时段各最优的暴雨强度总公式及误差值(表 2)。可见，所得最优暴雨强度公式除北碚、巴南站1991—2013年根据年多个样法选样采用皮尔逊Ⅲ型、耿贝尔分布外，其余均采用指数分布概率分布拟合，且采样方式均为年多个样法。下面将从1981—2013、1991—2013年两时段各选一个最优暴雨强度公式进行对比分析，从中选择暴雨强度值大的公式为该站暴雨强度公式。

2.2 不同年限资料的暴雨强度比较 2.2.1 沙坪坝站不同年限资料的暴雨强度公式比较

对沙坪坝站1981—2013、1991—2013年两时段最优的暴雨强度公式进行对比，分析各历时暴雨强度差值百分率。由表 3可以看出，10、15、20、30、45、60 min在3 a以上重现期，根据1981—2013年资料选样的最优暴雨强度公式计算结果比1991—2013年偏大，其余历时的重现期基本偏小。1981—2013年资料选样的最优暴雨强度公式计算结果比1991—2013年偏小在0.16%~2.17%之间。计算1981—2013、1991—2013年两时段最优暴雨强度公式不同重现期的平均绝对均方差可以看出(表 4)，1991—2013年资料选样的最优暴雨强度公式平均绝对均方差(0.032 mm·min^-1)小于1981—2013年(0.036 mm·min^-1)。因此，选择1991—2013年资料推求的最优暴雨强度公式。

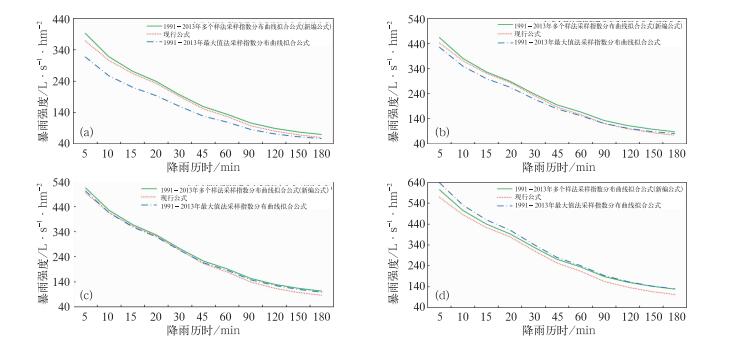
近年来，有学者比较了年最大值法与年多个样法推求暴雨强度公式的差别，建议编制暴雨强度公式时采用年最大值法选样(周玉文，2011；邓培德，2006)。本文统计了沙坪坝站1991—2013年年最大值法、年多个样法推求的暴雨强度公式不同重现期的暴雨强度值。结果表明：在低重现期部分(10 a以下)，年多个样法的重现期大于年最大值法，差值在3%~24%，两者的重现期差值在5 a以下部分相差较大(图 1a和1b)，在2 a重现期相差达23.67%，而且在10 a以下重现期，年最大值法推求的暴雨强度值小于现行公式；在11~30 a重现期部分相差较小(图 1d)，差值在-3%~3%，在31~100 a重现期部分, 年多个样法的重现期小于年最大值法，差值在-8%~-3%。

根据现行规范关于城镇类型的定义，重庆市主城区属于特大城市，《重庆市主城区排水(雨水)防涝综合规划》规定，雨水管渠设计时非中心城区的重现期采用3~5 a，中心城区及重要地区采用5 a重现期，对下立交、地道和下沉广场等采用30 a重现期。可见，重庆市主城区雨水管渠设计重现期选用主要范围为30 a以下。因此，选择基于1991—2013年资料根据年多个样法选样采用指数分布曲线拟合推求的暴雨强度公式为沙坪坝站的新编公式：

$q=\frac{1214.781(1+0.620\text{lg}P)}{{{\left( t+5.018 \right)}^{0.562}}}$

(2)

2.2.2 巴南、渝北、北碚站不同年限资料的暴雨强度公式比较

对巴南、北碚(表 5)、渝北站1981—2013、1991—2013年两时段最优的暴雨强度公式计算结果进行对比，结果显示，3站各历时、不同重现期的暴雨强度差值百分率不同，巴南、北碚站根据1981—2013年资料选样的最优暴雨强度公式计算结果比1991—2013年偏大，渝北站则相反。如渝北、北碚、巴南站5 a重现期180 min的暴雨强度差值百分率分别-6.59%、1.53%、6.23%；重现期2~100 a平均为：-4.8%、3.13%、4.6%。北碚和巴南站1981—2013年、渝北站1991—2013年的最优暴雨强度公式不同重现期的平均绝对均方差均满足现行规范要求(表 2)；相同时段的年最大值法与年多个样法选样推求的最优暴雨强度公式比较结果与沙坪坝站相同，即在10 a以下重现期部年多个样法的重现期大于年最大值法，在11~30 a重现期部分相差较小，甚至趋向一致，重现期在31~100 a年多个样法的重现期小于年最大值法。因此，巴南和北碚站选择基于1981—2013年、渝北站选择基于1991—2013年资料根据年多个样法选样采用指数分布曲线拟合推求的暴雨强度公式：

北碚:

$q=\frac{981.058(1+0.542\text{lg}P)}{{{\left( t+5.557 \right)}^{0.528}}}$

(3)

巴南:

$q=\frac{1857.828(1+0.672\text{lg}P)}{{{\left( t+8.633 \right)}^{0.697}}}$

(4)

渝北:

$q=\frac{1293.949(1+0.672\text{lg}P)}{{{\left( t+8.175 \right)}^{0.575}}}$

(5)

2.3 新编暴雨强度公式合理性分析 2.3.1 沙坪坝站暴雨强度公式合理性分析

沙坪坝站各历时年最大平均降水量的最大值在各时期均有出现(表 6)，1981—2013年各历时变化幅度分别为：-0.6、-0.5、-1.2、-1.5、-1.4、-1.5、-1.6、-0.9、0.1、1.0和1.6 mm·(10 a)^-1，1991—2013年11个历时年最大降水量与1981—2013年的变化趋势并不相同，变化幅度分别为：-0.7、-0.9、-1.0、-1.0、-0.2、0.2、1.4、1.0、1.5、1.9和1.9 mm·(10 a)^-1，其中5、10、15、20和30 min呈减少趋势外，其余6个历时呈增加趋势。

现行重庆市暴雨强度公式所用资料源于1973年以前，资料陈旧，且只有8 a样本数据，不能反映当前的降雨特征；公式的平均绝对均方差(0.087 mm·min^-1)不满足现行规范的不宜大于0.05 mm·min^-1的要求(邱兆富等，1999)。而新编沙坪坝站暴雨强度公式所用资料为近30 a的降雨记录，样本充足且能反映当前的降雨特征，新编公式平均绝对均方差为0.027 mm·min^-1。显然，沙坪坝站新编的暴雨强度公式的精度要明显优于现行公式。而且，新编的暴雨强度公式在不同重现期和不同降雨历时的暴雨强度值均大于现行公式(图 1)，2~100 a重现期的差值在1.5%~24.8%。可见，沙坪坝站利用近23 a资料推算的暴雨强度公式是合适的。

2.3.2 巴南、渝北、北碚站暴雨强度公式合理性分析

巴南、北碚(表 7)、渝北站1981—2013年各历时年最大平均降水量的最大值在各时期均有出现。从线性变化趋势来看，北碚、巴南站1991—2013、1981—2013年11个历时年最大降水量均呈减少趋势，但1981—2013年减少幅度更大。如北碚站1981—2013年各历时减少幅度分别为：-0.4、-0.8、-0.8、-2.9、-2.8、-2.3、-3.6、-2.9、-1.9、-1.9和-2.6 mm·(10 a)^-1；1991—2013年各历时分别为：-1.8、-2.6、-2.5、-0.8、-0.9、-1.1、-2.3、-3.2、-0.9、-2.4和-2.1 mm·(10 a)^-1。渝北站两时段的变化趋势与巴南、北碚站相反。这说明北碚、巴南站使用近33 a、渝北站使用近23 a资料推算暴雨强度公式是合理的。

3 暴雨强度公式适用性分析 3.1 各历时不同重现期暴雨强度的区域差异

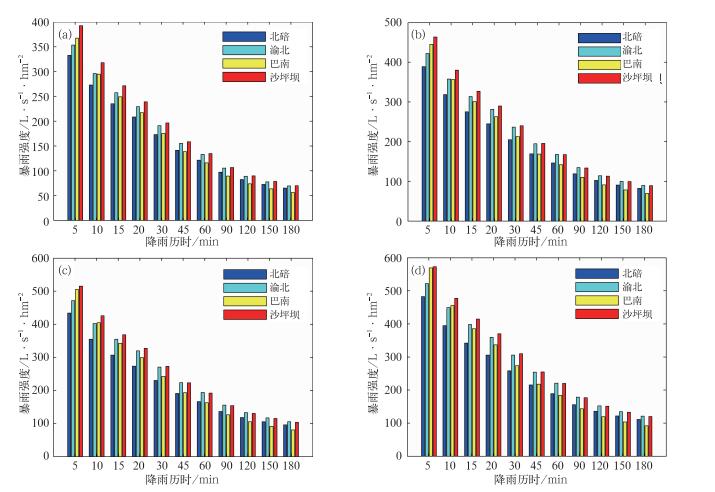
各历时暴雨强度基本以沙坪坝为最大(图 2)，在重现期2 a时北碚、渝北、巴南站各历时相对于沙坪坝站的差值百分率分别为：-8.1%、-3.9%、-13.3%，渝北站的暴雨强度值稍大于北碚站。

3.2 各历时最大降水量空间分布特征

重庆市主城9区除沙坪坝、北碚、巴南、渝北站有国家气象站外，其余5区(渝中、南岸、江北、九龙坡和大渡口区)没有长序列的气象观测资料，只有2010—2013年近4 a自动气象站的降水资料。针对暴雨具有明显的局地特征，根据重庆主城区4个国家气象站和107个自动气象站降雨资料，分析重庆主城区暴雨分布特征和区域代表性，对以沙坪坝、北碚、渝北和巴南4个国家气象站雨量为样本编制的暴雨公式适用范围作合理划分，分析各暴雨公式适用区域，以满足重庆主城区的室外排水规划设计需要。

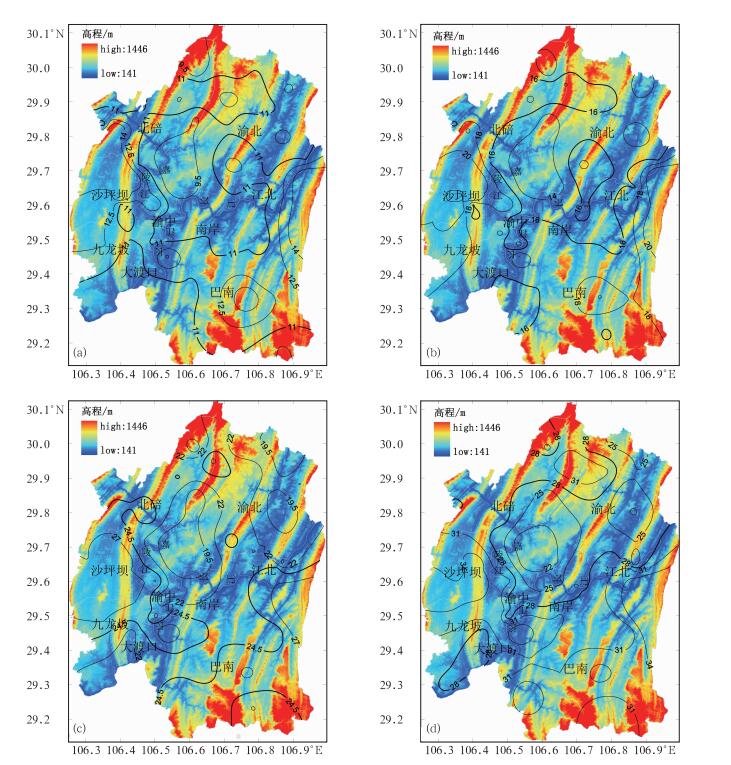
利用国家气象站和区域自动气象站近4 a逐年逐分钟降水资料，按年多个样法取样建立统计样本，计算每站每个历时的平均值，绘制空间分布图(图 3)。由于自动气象站的资料序列时间较短(只有4 a)，需对近4 a资料进行时间代表性分析。比较近4 a和近23 a的样本序列(表 8)可以看出，沙坪坝、北碚、巴南、渝北4个国家气象站近4 a暴雨强度样本序列均比近23 a的小，符合近年来重庆主城区极端降水事件减少(张天宇等，2011)及各历时暴雨强度基本减小的事实。

各历时平均最大降水量空间分布趋势基本一致，本文仅给出了10、20、45和90 min平均最大降水量分布图(图 3)，可见，11 mm(图 3a)、16 mm(图 3b)、24.5 mm(图 3c)和28 mm(图 3d)等值线基本沿长江、嘉陵江，主要形成了3个不同降水量级的区域，分别以长江和嘉陵江之间的地区为最大，长江以南的地区次之，长江和嘉陵江以北的地区最小。

3.3 重庆市主城区暴雨强度公式适应范围

根据重庆主城区各历时最大降水量分布特征和各地暴雨强度的比较结果和规划、设计上的安全及使用上的方便，短历时最大降水量略为偏小、分布特征比较接近的地区使用稍大地区的暴雨强度公式，根据此原则划定各暴雨强度公式使用区域分布(图 4)。重庆主城区各地的暴雨强度公式适用范围如下：(1) 沙坪坝站暴雨强度公式适用范围：长江和嘉陵江之间的地区，包括：沙坪坝、渝中、九龙坡、大渡口区和部分北碚区(嘉陵江以南区域)。(2) 巴南站暴雨强度公式适用范围：长江以南地区，包括：巴南、南岸区。(3) 渝北站暴雨强度公式适用范围：长江和嘉陵江以北的地区，包括：渝北、江北区和大部分北碚区(嘉陵江以北区域)。(4) 北碚站暴雨强度公式不使用。北碚站暴雨强度公式计算结果略小于渝北站，北碚站以北(南)短历时最大降水量空间分布与渝北站(沙坪坝)基本一致，故分别用沙坪坝(北碚的嘉陵江以南区域)、渝北站(北碚的嘉陵江以北区域)暴雨强度公式代替。

4 结论

(1) 基于年最大值法、年多个样法选取的统计样本，采用皮尔逊Ⅲ、耿贝尔分布、指数分布曲线拟合出重现期—暴雨强度—降雨历时关系表，使用最小二乘法求解公式参数，得到暴雨强度公式，检验结果表明，采用年多个样法取样推求的暴雨强度公式精度最高。

(2) 沙坪坝、北碚、巴南、渝北站年最大值法与年多个样法选样推求的暴雨强度公式在10 a以下重现期部分年多个样法的暴雨强度值大于年最大值法，且该重现期内沙坪坝站年最大值法公式的暴雨强度值小于现行公式；在11~30 a重现期部分年多个样法的暴雨强度值与年最大值法相差较小，甚至趋向一致；重现期在31~100 a年多个样法的暴雨强度值小于年最大值法。

(3) 分别选取1981—2013、1991—2013年两时段误差最小的暴雨强度公式，通过对比确定：巴南、北碚站选用基于1981—2013年降水数据根据年多个样法取样采用指数分布曲线拟合推算的暴雨强度公式；渝北、沙坪坝站选用1991—2013年降水数据根据年多个样法取样采用指数分布曲线拟合推算的暴雨强度公式。沙坪坝站新编暴雨强度公式不同历时不同重现期的暴雨强度值均比现行公式大且精度更高。

(4) 重庆主城区各历时降水量具有明显的局地特征，根据各历时暴雨强度分布和从安全与实际操作的角度确定了新编暴雨强度公式的使用范围：沙坪坝站暴雨强度公式适用于长江和嘉陵江之间的地区，包括沙坪坝、渝中、九龙坡、大渡口区和部分北碚区(嘉陵江以南区域)；巴南站暴雨强度公式适用于长江以南地区，包括巴南、南岸区；渝北区暴雨强度公式适用于长江和嘉陵江以北的地区，包括渝北、江北区和大部分北碚区(嘉陵江以北区域)；北碚暴雨强度公式不使用。