目前我国采暖热浪费情况仍然严重。开展气象节能研究是北方省(区、市)的一个重要任务,即根据气象预报调节能源使用量的方法,温度低时增加燃气和电力对取暖的供应,反之,减少取暖的供应,达到节能目的。在采暖系统运行期间,建筑物的耗热量不仅与供热面积、供热流量、供水温度、回水温度有关,更决定于室外温度等气象条件的影响,这些条件每时每刻都在变化。如前所述,供暖部门必须准确地掌握温度的实时变化情况,才能根据气温的随时变化及时调整供暖温度。我国气象部门多年来开展了气温和供暖气象节能技术研究,王志斌等(2005)研究了城市集中供热节能气象预报系统,陈正洪等(2005)、霍秀英等(1990)和车少静等(2002)采用统计预报的方法,提供常规的气象预报和日供、回水温度预报。由于这些方法自动化程度低,已经无法满足用户快速调整供暖的要求。探索新的预报方法,提供更精细的供暖参数是气象部门刻不容缓的责任。
欧洲地区如冰岛、土耳其及芬兰等国家有着丰富的地热资源,一些供暖单位利用地热的热量给建筑物供暖,由于这种热量往往达不到建筑物所规定室内温度,所以一般还需增加人工供热。为了使室内温度达到规定值,Valdimarsson等(1989)、Valdimarsson(1993)、Yildirim等(2003; 2006)和Nappa(2002)利用能量平衡原理,根据建筑物的实况温度(实时室内温度)和相应的外界气温来计算需增加的热量,既满足了供暖需求也节约了能源。
国内供暖多以小区为单位运行,需供暖的面积远大于国外的单栋屋型,热水在管道中流动的时间比较长,对室内温度的调节需要一定时间的提前量,照搬国外那种依靠气温实况来调节室温的做法,无法满足实际供暖需求,需要依托数值天气预报开展相关的供暖研究。
目前北京气象局已开发出精细化的快速更新数值预报系统(BJ-RUC),其预报要素包括未来24 h的逐时温度、湿度、风速和气压等基本气象要素,每3 h更新一次(范水勇等,2008; 2009;李青春等,2011),魏东等(2010;2011) 的研究表明无论其预报的基本要素, 还是计算的物理量, 12 h时效内的预报误差较小,与实况的一致性较好。总体来说,BJ-RUC对站点要素预报的变化趋势较好,准确率较高,具有很好的参考价值。该系统为开发气象服务新技术提供了条件,本研究的模型中就使用BU-RUC的预报产品。下面介绍本文研制的小区供热系统的供、回水温度预报模型。使用数值模拟方法制作供回水温度在国内尚属首次,该方法的运用使精细化的自动供暖气象节能服务成为可能。
1 供暖系统的物理模型原理简介经典的热学理论认为一般的民用住宅或房间的热平衡得到的热量主要是散热器和太阳辐射进入室内的热量。失热量则由维护结构传热耗热、门窗渗入室内的冷空气的耗热量(冷风渗透耗热量)和由门、孔洞及相邻房间侵入的冷空气耗热量(冷风侵入耗热量)组成。由于模拟这个过程非常复杂,因此必须对上述热量得失进行一定的简化,才能实现预报应用。首先,由于建筑物及管网随时间的变化比室外温度的变化慢得多,对短的温度间隔(如对本文的时间步长360 s来说小得多)可以忽略,即在本模型中忽略供暖系统的流体动力问题,将供暖系统考虑为准静力系统(Valdimarsson et al,1989;Valdimarsson,1993)。第二,考虑在实际供暖运营中,流量很少发生变化,因此在模拟过程中考虑恒定的流量,即管中流量不随时间变化。第三假设管道中没有热量损失,忽略管网中温度的下降。其他相对次要的热交换,如门、窗渗透的和侵入耗热及太阳辐射在本文中均予以忽略。
2 建筑物的供热量与热损失 2.1 建筑物的供热量供热量是需要提供给建筑物的热量,可以用供回水温度之差来表示,其方程(Valdimarsson et al,1989;Valdimarsson,1993)为
| $ {{Q}_{\rm{supply}}}={{\mathit{M}}_{\mathit{w}}}{{\mathit{c}}_{\mathit{p}}}\left({{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{r}}} \right) $ | (1) |
式中,Qsupply为供热量(单位:kW);Mw是水流量,本文中为常量,取为25 kg·s-1; cp为水的热容量(单位:J·kg-1·℃-1),这里取为4.186;Ts为供水温度(单位:℃);Tr为回水温度(单位:℃)。式(1) 表示供热量是Mw、Ts和Tr的函数。
2.2 建筑物的热损失建筑物的热损失是天气条件和室内温度的函数,表示热损失是建筑物表面通过墙体向外界环境的传输的热损失量。其方程可以写成如下形式(Valdimarsson,et al,1989;Valdimarsson,1993):
| $ {{Q}_{\rm{loss}}}={{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}\left({{\mathit{T}}_{\mathit{i}}}-{{\mathit{T}}_{\mathit{o}}} \right) $ | (2) |
式中,Qloss为建筑物热损失(单位:kW),Ub为建筑物热交换系数(单位:W·m-2·℃-1),Ab为建筑物面积(单位:m2),Ub、Ab是与建筑物的热性质有关数,将在第六节详细介绍。
式(2) 表明热损失是室外、内温度的函数。Ti为室内温度,To为室外温度, 这里就是BJ-RUC预报产品。
3 室内温度预报模型根据前面的假定,在任何时间建筑物的所得到的热量都用来加热室内温度,那么建筑物可以用单一的热单元来模拟(Yildirim,2003;2006),可将微分方程写为流入建筑物中的净热量与室内温度的时间导数和建筑物热容量之间的一个表达式,即建筑物的净热量可以描述为如下方程:
| $ {{C}_{\rm{air}}}=\frac{\rm{d}{{\mathit{T}}_{\mathit{i}}}}{\rm{d}\mathit{t}}={{Q}_{\rm{net}}}={{Q}_{\rm{supply}}}-{{Q}_{\rm{loss}}} $ | (3) |
式中,Cair为建筑物热容量(单位:J·℃-1),是与建筑物的热性质有关的常数,Qnet是输送到建筑物中的净热量,将式(1) 和(2) 代入式(3),整理后, 可得到Ti的预报方程:
| $ \frac{\rm{d}{{\mathit{T}}_{\mathit{i}}}}{\rm{d}\mathit{t}}=-\frac{{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}}{{{C}_{\rm{air}}}}{{\mathit{T}}_{\mathit{i}}}+\frac{{{\mathit{c}}_{\mathit{p}}}}{{{C}_{\rm{air}}}}\left({{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{r}}} \right){{\mathit{M}}_{\mathit{w}}}+\frac{{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}}{{{C}_{\rm{air}}}}{{\mathit{T}}_{\mathit{o}}} $ | (4) |
微分方程(4) 可以容易地通过离散方法求解。求解后室内温度的表达式可写为:
| $ \begin{align} & \ \ \ \ \ \ \ \ {{\mathit{T}}_{\mathit{i}\rm{(}\mathit{i}\rm{)}}}=\frac{{{Q}_{\rm{supply(}\mathit{i}\rm{-1)}}}+{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}{{\mathit{T}}_{\mathit{o}\rm{(}\mathit{i}\rm{-1)}}}}{{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}}- \\ & \frac{{{\rm{e}}^{(-{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}\Delta t/{{C}_{\rm{air}}})}}\left[ {{Q}_{\rm{supply(}\mathit{i}\rm{-1)}}}+{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}({{\mathit{T}}_{\mathit{o}\rm{(}\mathit{i}\rm{-1)}}}-{{\mathit{T}}_{\mathit{i}\rm{(}\mathit{i}\rm{-1)}}}) \right]}{{{\mathit{U}}_{\mathit{b}}}{{\mathit{A}}_{\mathit{b}}}} \\ \end{align} $ | (5) |
式中下标(i-1) 表示前一时间步长的值,通过式(5), 当前时间步长的Ti可以通过前一时间步长获得。在本方案中初始时刻的Ti(0)(即Ti(i-1)中i=1时)取为20℃,即初始值取与北京市或小区物业所规定的标准室内温度值接近的值。To(i-1)是BJ-RUC预报的室外温度。Qsupply(i-1) 为前一时刻的供热量,由式(1) 可求得,Ts和Tr为初始值,根据经验分别为80℃和60℃。
具体算法中要取一个样本建筑物,将在第六节介绍。
4 供水温度预报模型建筑物的热是由锅炉提供的,锅炉可以看作是一个具有固定热量的源,其热量传输给流入其中的水。来自锅炉的出水温度为Tb,前面已经假设管道中没有热量损失,所以供水温度Ts等于锅炉的出水温度,即Ts=Tb。根据能量守恒原理,利用下面的关系式可计算锅炉的出水温度。
| $ \frac{\rm{d}{{\mathit{T}}_{\mathit{b}}}}{\rm{d}\mathit{t}}=\frac{{{Q}_{\rm{boiler}}}-{{\mathit{M}}_{\mathit{w}}}{{\mathit{c}}_{\mathit{p}}}\left({{\mathit{T}}_{\mathit{b}}}-{{\mathit{T}}_{\mathit{r}}} \right)}{{{M}_{\rm{boiler}}}{{\mathit{c}}_{\mathit{p}}}} $ | (6) |
式中,Tb为锅炉出水温度(单位:℃),t为时间(单位:s),Qboiler为锅炉热容量(单位:kW),这里取为600;Mboiler为锅炉水质量(单位:kg),这里取为1000。
式(6) 与(4) 类似,也可以由离散方法求解。求解后锅炉出水温度的表达式可写为:
| $ {{\mathit{T}}_{\mathit{b}}}(\mathit{t})=\frac{{{Q}_{\rm{boiler}}}-{{\mathit{M}}_{\mathit{w}}}{{\mathit{c}}_{\mathit{p}}}{{\mathit{T}}_{\mathit{r}}}-{{\mathit{Q}}_{\mathit{r}}}}{{{M}_{\mathit{w}}}{{\mathit{c}}_{\mathit{p}}}} $ | (7) |
这里:
| $ {{\mathit{Q}}_{\mathit{r}}}=\left[ {{Q}_{\rm{boiler}}}+{{\mathit{M}}_{\mathit{w}}}{{\mathit{c}}_{\mathit{p}}}\left({{\mathit{T}}_{\mathit{r}}}-{{\mathit{T}}_{\mathit{b}\rm{(old)}}} \right) \right]\rm{exp}\left(-\frac{\Delta \mathit{t}{{\mathit{M}}_{\mathit{w}}}}{{{\mathit{M}}_{\rm{boiler}}}} \right) $ | (8) |
式中,Tb(old)在前一时间步长(t)的锅炉出水温度, Δt为时间步长,这里取360 s。Tb=Ts,即t+Δt的供水温度Ts可以从式(7) 得到。其中初始值Tr与上相同取为60℃。
5 回水温度预报方程供热量方程式(1) 也可以通过下式(Yildirim,2003;2006) 来表述:
| $ {{Q}_{\rm{supply}}}={{U}_{\rm{he}}}{{A}_{\rm{he}}}\mathit{LMT}{{\mathit{D}}_{\rm{he}}}={{Q}_{\rm{he}}} $ | (9) |
式中,Uhe为散热器的热交换系数;Ahe为散热器面积;LMTDhe为对数平均温度差;Qhe为散热器供热量。
| $ \mathit{LMT}{{\mathit{D}}_{\rm{he}}}=\frac{\left({{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{i}}} \right)-\left({{\mathit{T}}_{\mathit{r}}}-{{\mathit{T}}_{\mathit{i}}} \right)}{\ln \left[ \left({{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{i}}} \right)/\left({{\mathit{T}}_{\mathit{r}}}-{{\mathit{T}}_{\mathit{i}}} \right) \right]} $ | (10) |
即建筑物散热器的性能主要依赖于供水温度和回水温度。
| $ P=\frac{{{Q}_{\rm{he}}}}{{{Q}_{\rm{he0}}}}={{\left(\frac{\mathit{LMT}{{\mathit{D}}_{\rm{he}}}}{\mathit{LMT}{{\mathit{D}}_{\rm{0}}}} \right)}^{n}} $ | (11) |
式中,下标(0) 表示供暖设备的一种设计供回水温度情况。n的具体数值由经验来确定。这里取为4/3。
将式(1) 和(10) 代入式(11) 后整理,可得到以下形式:
| $ \frac{{{\mathit{M}}_{\mathit{w}}}\left({{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{r}}} \right)}{{{\mathit{M}}_{\rm{0}}}\left({{\mathit{T}}_{\mathit{s}\rm{0}}}-{{\mathit{T}}_{\mathit{r}\rm{0}}} \right)}={{\left\{ \left. \frac{\frac{{{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{r}}}}{\ln \left[ \left({{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{i}}} \right)/\left({{\mathit{T}}_{\mathit{r}}}-{{\mathit{T}}_{\mathit{i}}} \right) \right]}}{\frac{{{\mathit{T}}_{\mathit{s}\rm{0}}}-{{\mathit{T}}_{\mathit{r}}}_{\rm{0}}}{\ln \left[ \left({{\mathit{T}}_{\mathit{s}\rm{0}}}-{{\mathit{T}}_{\mathit{i}\rm{0}}} \right)/\left({{\mathit{T}}_{\mathit{r}\rm{0}}}-{{\mathit{T}}_{\mathit{i}\rm{0}}} \right) \right]}} \right\} \right.}^{n}} $ | (12) |
式中,下标(0) 表示在设计情况下的状态,这里根据经验分别取Ti0、Ts0和Tr0为20℃、90℃和70℃,Ts是式(7) 计算出来的供水温度,Ti是由式(5) 计算出来的供水温度。另外本文中考虑恒定的流量,Mw=M0,对式(12) 进行化简可以得到回水温度的预报方程。
| $ {{\mathit{T}}_{\mathit{r}}}={{\mathit{T}}_{\mathit{i}}}+\frac{{{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{i}}}}{\rm{exp}\left[ {{\left(\frac{{{\mathit{T}}_{\mathit{s}}}-{{\mathit{T}}_{\mathit{r}}}}{{{\mathit{T}}_{\mathit{s}\rm{0}}}-{{\mathit{T}}_{\mathit{r}\rm{0}}}} \right)}^{(1-1/\mathit{n})}}\rm{ln}\left(\frac{{{\mathit{T}}_{\mathit{s}\rm{0}}}-{{\mathit{T}}_{\mathit{i}\rm{0}}}}{{{\mathit{T}}_{\mathit{r}\rm{0}}}-{{\mathit{T}}_{\mathit{i}\rm{0}}}} \right) \right]} $ | (13) |
方程两边都有Tr,采用迭代法可解出回水温度Tr,本文的迭代初值取为60℃。
6 样本建筑物及参数的计算 6.1 样本建筑物面积(Ab)和建筑物热交换系数(Ub)的计算样本建筑物选择与北京市海园物业供热单位类似的一栋建筑物(Lei,2004),建筑物一共6层,每层有4户,可分为A、B、C 3部分,建筑物的各部分面积可通过计算而得,如表 1所示。
|
|
表 1 样本建筑物的各部分面积(Ab,单位:m2) Table 1 The area of sample buildings (Ab, unit:m2) |
建筑物热交换系数是用于描述平流、对流和辐射而引起在建筑物和周围环境之间产生的热交换。
| $ {{U}_{\rm{total}}}=\frac{{{U}_{1}}{{A}_{1}}+{{U}_{1}}{{A}_{1}}+\cdots +{{U}_{n}}{{A}_{n}}}{{{A}_{\rm{total}}}} $ | (14) |
式中,Utotal为建筑物总热交换系数(单位:W·m-2·℃-1),Un为建筑物各部分(屋顶、地板、外墙和窗户)热交换系数(单位:W·m-2·℃-1),An为建筑物各部分面积(单位:m2),Atotal为建筑物总面积。由上面的公式可以得到如下表 2。
|
|
表 2 建筑物传热系数(Ub)、面积(Ab)和总热传热系数 Table 2 Heat transfer coefficient (Ub), area (Ab) and total heat transfer coefficient of buildings |
由表 2可以得到取样建筑物的总传热系数值(UbAb)为22940 W·℃-1。
6.3 样本建筑物总热质量(Cair)的计算建筑物的热质量是表示建筑物存储热量的一种能力。样本建筑物的总热质量由各个部分(屋顶、地板、外墙和窗户)的热质量之和得到(Lei et al,2009)。建筑物热质量公式如下:
| $ {{C}_{\rm{air}}}={{m}_{\rm{air}}}{{\mathit{C}}_{\mathit{v}}}={{\rho }_{\rm{air}}}{{V}_{\rm{building}{{\mathit{C}}_{\mathit{v}}}}} $ | (15) |
式中,mair为空气质量,ρair为空气密度,Vbuilding为建筑物的体积,可采用式(14) 的同样方法求得, cv为热容量,计算结果列于表 3和表 4。
|
|
表 3 建筑物材质特性 Table 3 Material characteristics of buildings |
|
|
表 4 建筑物总热质量Cair Table 4 Total thermal mass of buildings Cair |
由表 4可以知道,建筑物的总热质量(Cair)为6249169 kJ·℃-1。
7 逐时供、回水温度预报的模拟试验 7.1 室外温度资料BJ-RUC系统每隔3 h(00—21时),生成一个室外温度预报产品,每个起始预报时次又能够提供未来24 h逐时的气温预报。因此,根据BJ-RUC提供的各个时次的气温预报产品,代入上述各个方程,得到预报结果。
7.2 计算流程首先,利用BJ-RUC系统预报的逐时To预报值,将逐时To在所要求的时间步长(360 s即0.1 h)内进行插值。其次确定初始Ti0、Ts0和Tr0。模拟循环开始,利用式(5) 计算Ti。接着用式(7) 计算, 然后利用式(13) 计算Tr。如此循环,就得到间隔为0.1 h未来时刻的Ti、Ts和Tr预报值。
7.3 试验模拟结果与海园物业供暖实况的对比北京市采暖季节大约开始于11月中旬和结束于3月中旬,模拟时间取10年3月1—15日。取该时段北京市海园物业供暖单位供、回水温度实况监测值与本模式的预报值进行对比。计算结果表明模拟值与要求的供暖温度(20℃)的均方根误差为0.25℃, 海园物业供暖实况与其的均方根误差为1.53℃。Ts和Tr模拟值与实况值之间的均方根误差分别为3.69℃和3.80℃,即预报模式具有一定的预报能力。图 1是对比情况。

|
图 1 2010年3月1—15日BJ-RUC预报的室外温度与实况(a)、模拟的室内温度(b)和海园物业供暖实况(c) Fig. 1 Forecasted outdoor temperature and observation (a), simulated (b, dashed line) and observed (c, solid line) indoor temperature in Haiyuan Community in 1-15 March 2010 |
从图 1a可见,BJ-RUC预报的温度与实况值基本一致。图 1b中模拟的Ti在20℃上下波动。海园物业供暖实况Ti则开始时低于20℃,之后慢慢回升,后又逐渐下降。即按模拟结果供暖要比原来的供热情况好,既可以达到供暖要求的温度,又实现室内温度基本稳定的效果。陈正洪等(2005)发现,在实际供暖中,当环境温度很低时,供热量略显不足,但当环境气温较高时,供热量远大于理论值,环境温度越高,浪费越大。本研究以室内温度的稳定为标准,确定室外温度与供、回水温度的关系,当预报室外温度升高时,供暖部门可减少供热,使供、回水温度下降,即达到减少浪费,实现节能的目的。而当预报室外温度降低时,供暖部门可增加供热,提高供、回水温度,使居室温度达标。
从图 2可以看到如下几点:
|
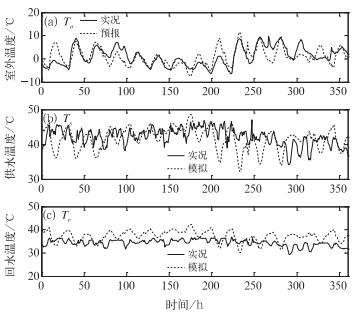
图 2 2010年3月1—15日BJ-RUC提供的室外温度预报和实况(a),逐时Ts模拟值与海园物业供暖实况Ts对比图(b),逐时Tr模拟值与海园物业供暖实况Tr对比图(c) Fig. 2 (a) Predicted outdoor temperature (dashed line) by BJ-RUC and observation (solid line), (b) hourly simulated values (dashed line) and observed supply water temperature (solid line) in Haiyuan Community, (c) hourly simulation values and observed returen water temperature in Haiyuan Community in 1-15 March 2010 |
(1) 图 2a表明室外温度的预报和实况有很好的一致性,证明了BJ-RUC的可用性。
(2) 从图 2a~2c可以看出,供水温度Ts和回水温度Tr具有基本一致的变化趋势,而Ts、Tr和室外温度To有相反的变化趋势,也就是当室外温度下降时,供水温度Ts和回水温度Tr随之上升,当室外温度上升时,供水温度Ts和回水温度Tr随之下降,总之,供水温度与回水温度能够随着室外温度的变化而及时做出相应的调整,从而能够实现供、回水温度随着室外温度的变化进行自动调整。
(3) 从图 2中可见在3月1—2日(0—48 h)最低室外温度To出现在33 h(-4.8℃),对应模拟的Ts为45.1℃,Tr为39.8℃;后To上升,在42 h达到8.9℃,Ts则下降到35.8℃,Tr为32.9℃;在223~224 h,达上旬的最低值-6.4℃,Ts达45.6~46.8℃,Tr为40.1~40.2℃;在258 hTo达最高值9.4℃,Ts下降到34.83℃,Tr为31.7℃,图中很好地呈现了Ts、Tr与To的变化关系。
(4) 从上述(3)和冯涛等(2012)表明一般北京的Ts在35~60℃范围内,Tr在30~45℃范围内,即基础值比较高, 误差相对基础值是比较小的。另外, 因为水的热容量(4200 J·kg-1·℃-1)比空气(1030 J·kg-1·℃-1)大,所以对温度的敏感性低于空气。Ts和Tr模拟值与实况值之间的均方根误差分别为3.69℃和3.80℃是比较小的,合适的。
8 结论(1) 该方法摆脱了统计方法处理繁琐、研发效率低、精细化和自动化程度不高的局限性,为供暖气象节能精细化、通用化和供暖调控自动化做了一点尝试,使提供更广泛的小区供暖气象节能服务成为可能。
(2) 上述进行的Ti、Ts和Tr的对比,即预报模式具有一定的预报能力。该结果虽然该预报模式在设计过程中对得、失热等做了一定的简化,但是仍然具有一定的预报能力。另外随着气象部门数值预报系统的更新,模式的预报能力也将逐步改进。
(3) 文章采用的方程中,省略了太阳辐射,估计对于白天的室内温度有一定影响(预报低于实况)。在未来的工作中将探讨订正太阳辐射的方法,也许会有利于降低供回水温度的误差和进一步节能。
车少静, 傅炳珊, 石志增, 2002. 石家庄市采暖期气象服务系统[J]. 气象, 28(5): 50-52. DOI:10.7519/j.issn.1000-0526.2002.05.013 |
陈正洪, 胡江林, 张德山, 等, 2005. 城市热岛强度订正与供热量预报[J]. 气象, 31(1): 69-71. DOI:10.11676/qxxb2005.008 |
范水勇, 郭永润, 陈敏, 等, 2008. 高分辨率WRF三维变分同化在北京地区降水预报中的应用[J]. 高原气象, 27(6): 1181-1188. |
范水勇, 陈敏, 仲跻芹, 等, 2009. 北京地区高分辨率快速循环同化预报系统性能检验和评估[J]. 暴雨灾害, 28(2): 119-125. |
冯涛, 李迅, 丁德平, 等, 2012. 北京地区主要气象要素与冬季供暖关系研究[J]. 气象, 38(3): 322-328. |
霍秀英, 王锋, 1990. 温度预报在集中供热采暖中的应用[J]. 气象, 16(2): 51-54. DOI:10.7519/j.issn.1000-0526.1990.02.012 |
李青春, 程丛兰, 高华, 等, 2011. 北京一次冬季回流暴雪天气过程的数值分析[J]. 气象, 37(11): 1380-1388. DOI:10.7519/j.issn.1000-0526.2011.11.008 |
王志斌, 张德山, 王保民, 等, 2005. 北京城市集中供热节能气象预报系统研制[J]. 气象, 31(1): 75-78. DOI:10.7519/j.issn.1000-0526.2005.01.018 |
魏东, 尤凤春, 范水勇, 等, 2010. 北京快速更新循环预报系统(BJRUC)模式探空质量评估分析[J]. 气象, 36(8): 72-80. DOI:10.7519/j.issn.1000-0526.2010.08.010 |
魏东, 尤凤春, 杨波, 等, 2011. 北京快速更新循环预报系统(BJRUC)要素预报质量评估[J]. 气象, 37(12): 1490-1497. |
Lei Haiyan.2004.Simulation of district heating system in Tianjin, China.UNU-GTP Number 8, Reports, 131-158, Reykjavík, Iceland.
|
Lei Haiyan, Pall Valdimarsson.2009.District heating modeling and Simulation.Proceedings, Thirty-Fourth Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, California, February 9-11.
|
Nappa M.2000.District heating modeling.Geothermal Training Workshop at University of Iceland.
|
Yildirim N, Gokcen G.2003.Modelling of Low Temperature Geothermal District Heating System.Proceedings of the First International Exergy, Energy and Environment Symposium 13-17 July 2003, Izmir, Turkey.
|
Yildirim N, Toksoy M, Gulden G, 2006. District heating system design for a university campus[J]. Energy and Buildings, 38: 1111-1119. DOI:10.1016/j.enbuild.2006.01.004 |
Valdimarsson P, 1993. Modelling of geothermal district heating systems[J]. University of Iceland, 115: 37-82. |
Valdimarsson P, Jdnsson V K.1989.Simulation of geothermal district heating systems.Proc 11th New Zealand Geothermal Workshop, 127-132.University of Iceland, 6, IS-101 Reykjavik, Iceland.
|
 2015, Vol. 41
2015, Vol. 41 