2. 河北省气象科学研究所,河北省气象与生态环境重点实验室, 石家庄 050021;
3. 山西省浑源县气象局,浑源 037400;
4. 成都信息工程大学大气科学学院,高原大气与环境四川省重点实验室,成都 610225
2. Hebei Key Lab for Meteorology and Eco-Environment, Institute of Meteorological Science of Hebei Province, Shijiazhuang 050021;
3. Hunyuan Meteorological Station of Shanxi Province, Hunyuan 037400;
4. College of Atmospheric Sciences, Plateau Atmosphere and Environment Key Laboratory of Sichuan Province, Chengdu University of Information Technology, Chengdu 610225
黄淮区域地处我国南方雨量丰沛和北方干旱少雨的过渡地带,气候异常成因复杂,降水预报准确率较低。从气候特征看,黄淮区域汛期降水量最大,集中了年降水量的45%~65%。该地区降水的年际变率较大,最多年与最少年降水量相差悬殊(张永领等,2003),因此准确预测黄淮区域汛期降水对于防灾减灾具有特别重要的意义。
在进行中小河流的山洪、泥石流预报预警决策中,区域(流域)降水的准确预报是决策的重要技术支撑。然而,由于降水是由一系列复杂物理过程所形成,是一定气候背景下并在大尺度环流与中小尺度系统共同相互作用形成的结果,同时也易受当地的下垫面以及本地热力场和动力场等的影响(闵晶晶等,2010;曹晓钟等,2008)。因此相对于气压、温度、风速等天气要素预报的改善,降水预报的准确率提高相对缓慢,使之成为天气预报和气候预测最有预报难度的天气要素之一(Fritsch et al,1998;Sanders,1986;Mullen et al,2001)。
目前对外提供服务的确定性降水预报只能给出有无雨预报和分等级(小雨、中雨、大雨、暴雨等)的预报,没有表达出降水出现的可能性大小。由于预报的不确定性总是存在,如果能将不确定定量表达出来,不同的用户就能根据自身的需求和对气象的依赖程度做出不同的选择(杜钧,2002;杜钧等,2010),因此概率预报变得越来越有价值。
有研究表明,一个概率预报系统比一个与其质量相当的确定性预报系统具有更大的价值,这是因为用户可以根据自身的需要选择一个适当的概率阈值(Murphy et al,1987)。降水概率预报能够定量地给出降水出现的可能性大小,它用概率值大小反映降水的不确定性。在降水概率预报技术研究方面,国内外已有很多研究成果,主要方法是利用数值预报产品,通过统计预报方法建立概率预报方程等方法(陈超辉等,2009)。如事件概率回归估计方法(周兵等,1996),非线性多因子动态组合方法(邵明轩等,2003),概率回归降水等级预报(赵声蓉等,2009)等。概率预报已在气象、水文、地震、海洋、交通等预报中获得应用。如Krzysztofowicz(1993)已将降水概率预报应用于流域水文预报中;美国国家海洋大气局的7天降水预报是以概率形式发布的;在我国北京等一些城市也开展了降水概率预报(周兵等,1996; 田付友等,2014;张宇彤等,2013)。降水的概率预报比起确定性的预报更能满足交通、航海、航空、农业、水利和电力等部门的需求,能大大提高天气预报的使用效益,为科学决策提供依据,所以概率降水预报将成为今后天气预报应用的主要发展方向。
目前,概率预报大体划分为两类:第一类是利用数值模式(集合预报)计算降水出现的概率;第二类是利用模式产品结合实测资料,采用统计方法制作降水概率预报。近年来,国内外学者引入多种新的统计方法,如多重判别分析方法(吴蓁等,1999)、卡尔曼滤波方法(寗春蓉等,2004)、神经网络方法(Hall et al,1999)、K最近邻域非参数估计技术等(曾晓青等,2008)。但是上述这些方法多数是基于线性相关的基础上,在处理一些像降水这样具有非线性特征的气象要素时具有较大的局限性。此外,不同的气候背景和环流形势下的降水机理不同,不同地域的降水性质也不会相同,因此所涉及到的预报模型和模型选取的预报因子也不同。对于在降水分区基础上的集成降水预报方法表明,采用天气分型的预报方法较不分型有很大的优势。赵翠光等(2011)在降水客观分区的基础上,对华北及周边地区进行夏季降水预报,也取得了较好的效果。
Logistic回归方法不仅对非正态母体适用,而且对既离散又连续变量的因子也能适用,建立模型时工作量并不过于复杂,从理论、数学模型及实用上都具有很强的生命力。该方法最初由Cox(1966)提出设想,后经Day等(1967)发展,又由Anderson(1972)改进的,Logistic模型在国外被广泛应用于概率天气预报的业务预报系统,极大改善了预报效果(Walker et al,1967;Bocchieri,1979;Applequist et al,2002)。Applequist等(2002)比较了Logistic回归、线性回归、多重判别分析、神经网络和分类系统等五种统计方法,验证了Logistic回归在概率降水方面效果最好,Logistic方法也逐渐被国内学者熟悉并应用于业务中,并取得了较好的预报效果(陈启槐等,1999;黄永新,1997)。
但是基于历史降水时空分布基础上分区的降水概率预报方法尚不多见。基于上述思路,本文利用1961—2010年50年黄淮地区的341个观测站夏季日降水量观测资料和美国NCEP释放的高分辨率全球模式预报系统CFSv2的后预报资料,在对黄淮地区夏季日降水进行分区的基础上,采用Logistic方法建立各区域代表站的概率降水预报方程,并对其预报结果进行了检验并与T213集合预报进行了比较,以探索分区基础上的概率降水预报方法的建立。
1 黄淮地区夏季降水分区为了得到我国黄淮地区夏季日降水的分区特征,本文使用国家气象信息中心整编的全国日降水资料,选取1961—2010年6—8月每日20时至20时(北京时,下同)的黄淮地区(32°~40°N、110°~123°E)内341个观测站的日降水,资料长度为50年。
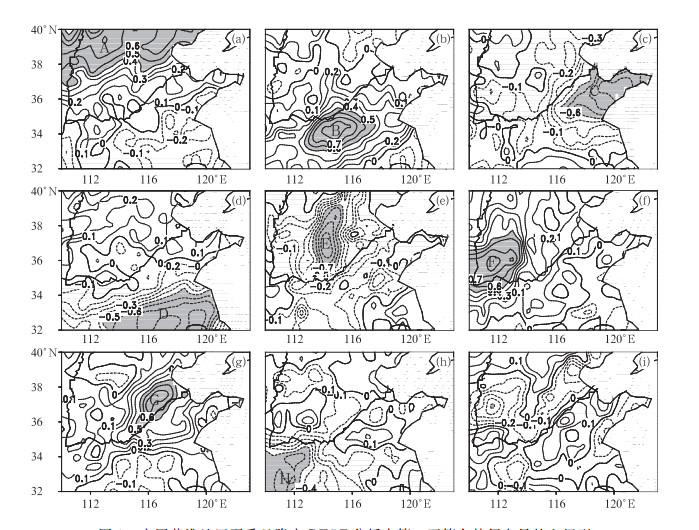
先对降水资料进行标准化处理。将研究区域内50年无缺测值的341个观测站的日降水量资料进行EOF展开,得到前十个主分量旋转前后的方差及累计方差,前四个模态所占的累计方差贡献率为52.41%,且这四个模态均通过了North等(1982)提出的计算特征值误差范围的检验。通过EOF的展开分析可以看出(图略),黄淮地区的夏季日降水存在南北差异,主要特点为东西向分布,也有少数南北分布的情况,但是仅从这四个模态上不能更为精细地得到降水的分区特征分布。因此,在EOF分析的基础上,再进一步做最大正交方差旋转进行REOF展开。旋转后发现载荷的贡献率比旋转之前分布均匀,因为旋转后各主成分的意义着重表现空间的相关性分布特征,高载荷只集中在某较小区域,同时使其他大部分区域的载荷尽可能地接近。对前十个主分量(累计方差贡献率为70.26%)进行REOF展开发现,从第九个主分量开始,旋转后的模态已没有明显高载荷区(图 1)。图 1的阴影区为旋转因子载荷绝对值 > 0.5的载荷高值区,且前8个主分量(累计方差贡献率为66.08%)旋转后的模态高载荷区已经能把整个区域覆盖,因此将这8个高载荷区作为分区依据。旋转后的第一模态高载荷区为正值,位于研究区域的北部,即华北中南部地区,最大值0.82出现在天津武清(图 1a);旋转后的第二模态高载荷区为正值,位于黄河与淮河中间的区域,最大值为0.871,出现在河南太康(图 1b);旋转后的第三模态高载荷区为负值,位于山东半岛,绝对值最大值为0.871,出现在山东崂山(图 1c);旋转后的第四模态高载荷区为负值,位于淮河流域,绝对值最大值为0.834,出现在安徽定远(图 1d);旋转后的第五模态高载荷区为负值,绝对值最大值为0.88,出现在河北邯郸(图 1e);旋转后的第六模态高载荷区为正值,最大值为0.86,出现在山西翼城(图 1f);旋转后的第七模态高载荷区为正值,绝对值最大值为0.871,出现在山东夏津(图 1g);旋转后的第八模态高载荷区为负值,绝对值最大值为0.67,出现在河南栾川(图 1h)。为了确认上述八个变化区域之间的差异性,对这八个区域50年平均降水序列的t值和显著性水平进行了检验(表 1),从表 1看出大部分区域之间均通过了0.05的显著性水平检验,区域B和C检验的显著性水平虽然没有通过0.05,但是显著性水平较高。同时可以发现区域A和E、B和G、G和H的显著性水平分别为0.321、0.254、0.244,均没有通过0.05的显著性水平检验,说明区域A和E、B和G、G和H之间降水差异不明显。因此将区域A和E合并成为区域Ⅰ,区域B、G和H合并成区域Ⅱ。这样区域Ⅰ、区域Ⅱ与区域C、D、F共同组成区域Ⅰ—Ⅴ,再将区域Ⅰ—Ⅴ进行t检验,结果如表 2。区域Ⅰ—Ⅴ之间均通过了0.05的显著性水平检验,说明区域Ⅰ—Ⅴ之间存在显著地差异性,所以黄淮地区夏季降水主要区域可划分为五个区域(图 2)。
|
图 1 中国黄淮地区夏季日降水REOF分析中第一至第九特征向量的空间型 Fig. 1 Spatial patterns of the first to the ninth characteristic vectors of REOF for summer rainfall over Huang-Huai Region |
|
|
表 1 1961—2010年黄淮地区八个REOF降水分区差异显著性的t检验 Table 1 The t-test of significance of summer rainfall regional difference in eight areas of Huang-Huai Region during 1961-2010 |
|
|
表 2 1961—2010年黄淮地区五个降水分区差异显著性的t检验 Table 2 The t-test of summer rainfall significant difference in five main areas of Huang-Huai Region during 1961-2010 |
|
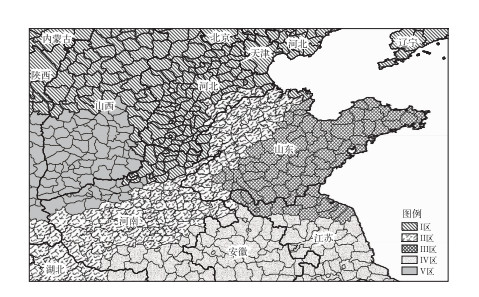
图 2 中国黄淮地区夏季降水分区 Fig. 2 Regional precipitation division over Huang-Huai Region in summer |
上述黄淮地区的五个夏季降水分区,决定了黄淮地区降水的主要特征。这为建立黄淮夏季降水分区日降水的概率预报模型奠定了基础,做好上述五个区域的降水预报就可以获得该区域降水预报成功的主要部分。
2 黄淮地区夏季降水分区代表站概率预报模型 2.1 建模资料建模需要较长的模式历史资料。选取的模式资料为1999—2009年的6—8月NCEP释放的高分辨率全球模式预报系统CFSv2第二版的后预报资料。该模式完全耦合了海洋、陆地和大气系统,并于2011年3月在NCEP投入业务运行,系统包括几乎所有数据同化资料和预报模块,它的后预报资料是通过对1971—2011年共32年的初始条件耦合进行再分析,形成的1982—2011年共29年的预报资料。模式的水平分辨率是0.5°×0.5°,垂直分辨率为37个气压层。降水观测资料是1999—2009年6—8月日降水资料,选取前日20时至当日20时的24 h累计降水量作为当日降水量。其中1999—2007年的资料建模,用2008—2009年的独立样本资料做预报检验。
2.2 概率预报方法在建立降水概率预报模型前,要对降水资料进行0、1化处理,当站点实测有降水时预报量记为1,反之为0。其他预报因子进行标准化处理。由于模式预报资料与站点实测降水资料空间位置不同,因此将模式资料中各要素利用反距离权重插值法插值到相应站点,再用于建立站点上的降水概率预报方程。在前面对黄淮地区夏季降水分区分析的基础上,在每个降水分区(图 2)选取1个站点,这些站点分别是区域Ⅰ的山西繁峙、区域Ⅱ的河南西平、区域Ⅲ的山东兖州和区域Ⅳ的河南正阳以及区域Ⅴ的山西翼城。这五个站点作为每个区域的代表站,采用Logistic回归方法建立降水概率预报模型。
Logistic回归模型常用于研究两元分类响应变量与诸多自变量间的相互关系。应用于降水概率预报时,如果某日有雨,即将两元分类响应变量Y记为1,如果没雨,将其记为0。为了说明该方法的思路,本文以有无降水概率预报来说明这种方法的建立,其他分等级的降水概率预报可以凭类似方法建立。对于响应变量Y有影响的p个自变量记为X1, X2, …, Xp。在p个自变量的作用下预报有雨的条件概率记为p=P(Y=1|X1, X2, …, Xp),那么Logistic回归模型表示为:
| $ \mathit{p} = \frac{{{\rm{exp}}\left({{\beta _0} + {\beta _1}{X_1} + {\beta _2}{X_2} + \ldots + {\beta _p}{X_p}} \right)}}{{1 + {\rm{exp}}\left({{\beta _0} + {\beta _1}{X_1} + {\beta _2}{X_2} + \ldots + {\beta _p}{X_p}} \right)}} $ | (1) |
式中,β0称为常数项或截距,β1,β2,…,βp称为Logistic回归模型的回归系数。从式(1) 中可以看出,Logistic回归模型是一个非线性的回归模型,自变量Xj(j=1, 2, …, p)可以是连续变量,也可以是分类变量或哑变量。对自变量Xj任意取值,β0 +β1X1+β2X2+… +βpXp总落在(-∞, +∞)中,因此式(1) 的比值,即p的取值,总在0~1之间变化,此为Logistic回归模型的合理性所在(汤银才,2013)。
2.3 预报因子的选取以往的研究经验表明,降水概率预报效果的好坏,不仅与预报方法有密切关系,选择合适的预报因子更为重要。故在选择因子时,必须选取与预报量相关且有物理意义的因子作为预备因子。研究表明从众多因子中客观地选出较好的因子可以提高预报效果(张诚忠,2001)。基于此,根据降水形成的三个天气学条件,分别选择CFSv2模式的高、中、低三个层次上的物理量预报因子17个作为预备预报因子。这些因子是每个站点上的850、700和250 hPa高度上的涡度、散度、位势高度、比湿和垂直速度等。利用这17个初选预报因子建立方程,并通过逐步回归方法剔除掉方程中没通过显著性检验的因子,得到最优因子建立方程。根据各区逐步回归筛选得到的预报因子,最终保留最优因子进入各站点的夏季降水概率方程,利用式(1) 在五个站点建立夏季降水预报概率方程。
3 预报效果比较分析与检验2.3节是利用1999—2007年的观测和模式资料建立的五个站点的降水概率预报方程,本节用2008—2009年的观测降水独立样本资料进行检验。为了比较本文在进行夏季降水天气分区基础上建立的Logistic回归概率预报模型在五个代表站的预报效果,本文模型预报的结果进行了确定性预报检验和概率预报检验与比较。确定性预报检验是与美国CFSv2模式的确定性预报结果、国家气象中心集合预报模式T213的集合平均预报结果进行了对比;概率预报检验是采用本文建立的概率预报模型和国家气象中心集合预报模式T213的概率降水预报进行对比的方式,这是因为T213集合预报水平分辨率(0.5625°×0.5625°)与美国CFSv2模式的分辨率较为接近。
3.1 确定性预报效果检验首先对得到的5个站日降水预报结果进行确定性检验,以便了解预报效果的大致情况。将5个站日降水的概率预报结果转化为确定性预报,分别与CFSv2模式的确定性预报结果、T213(记为CMA集合预报)的集合平均预报检验与比较。对于本文得到的0~1之间的概率预报,取预报概率0.5为有无降水的临界值,将预报概率值小于0.5记为无降水,反之记为有降水。这样即可对模型的降水预报进行TS评分。
由TS评分(图略)可以看出,本文Logistic回归降水概率预报模型的TS评分要高于CFSv2全球预报模式和CMA集合预报,这说明本文Logistic回归降水概率预报模型的预报效果相比于CFSv2模式的预报效果有所提高。本文Logistic回归模型的空报率小于漏报率,而CFSv2模式和CMA集合预报的空报率大于漏报率,且漏报率都比本文Logistic回归降水概率预报模型的低,其中CFSv2全球预报模式的漏报率几乎为零,也就是说本文Logistic回归降水概率预报模型的漏报率还有待改进。TS评分在一定程度上对降水发生的概率有一定依赖性,降水多的地区评分高,降水少的地区评分相对偏低,这不利于不同地区不同气候概率下预报的比较(王雨,2004)。不同地区有无降水的天数不是均匀分布的,因此以0.5作为判断有无降水的标准并不十分恰当,所以下面进行概率预报效果检验,从概率的意义上理解该预报性能。
3.2 概率预报效果检验采用Brier评分和Brier技巧评分来评价概率预报效果。Brier评分是由Brier于1950年提出的最早应用于降水概率预报评分的方法,也是气象上最常见的降水概率评分方法(Murphy,1973)。Brier评分定义了一种均方概率误差,该方法综合考虑了可靠性、分辨能力和不确定性。Brier评分已在定量降水概率预报评估中得到了广泛应用(赵琳娜等,2010;2015),其表达式如下:
| $ BS = \frac{1}{N}\sum\limits_{k = 1}^N {{{\left({{{\mathit{\hat x}}_k} - {x_k}} \right)}^2}} $ | (2) |
式中,N为预报总次数,
BSS评分用于评估相对于一个参考系统集合预报系统的预报性能,其公式如下:
| $ BSS = 1 - \frac{{BS}}{{B{S_{{\rm{ref}}}}}} $ | (3) |
BSref=s(1-s),s是被检验事件发生的气候概率。和BS不一样的是,BSS是正定向的。BSS为1时表示完全准确的确定性预报,BSS为0时表示系统的预报性能与参考系统相同,BSS小于0时表示系统的预报要差于参考系统。这里直接用观测得到的气候概率预报为参考系,用BSS技巧评分检验集成预报的降水概率的预报性能。可以将BSS化成如下形式:
| $ BSS = \frac{{B{S_{{\rm{res}}}} - B{S_{{\rm{rel}}}}}}{{B{S_{{\rm{unc}}}}}} $ | (4) |
式中,BSres是预报系统分辨率,BSrel是预报系统可靠性,BSunc是预报系统不确定性。BSS属性图可以将BSS的分辨率、可靠性等信息表现出来。
将本文Logistic回归降水概率预报模型得到的24 h降水概率预报与T213的集合预报24 h概率降水进行比较,表 3中列出了BS评分以及BSS评分。从表 3可以看出,CMA集合预报的BS评分都在0.3以上,CMA集合预报的BS评分值普遍比本文Logistic概率回归的BS评分值高,说明CMA集合预报的可靠性比本文Logistic概率回归的可靠性低,而本文建立的概率回归模型的预报BS评分都在0.20以下,说明概率回归的预报可靠性较CMA集合预报高。此外,从BSS的评分可以看出,本文概率回归预报的BSS评分均为正值,说明有预报技巧。而CMA集合预报的BSS评分均为负值,说明在本次检验中CMA集合预报的预报技巧低于检验样本的气候概率。总的来讲,本文Logistic回归降水概率预报模型在黄淮地区的预报效果比T213集合预报24 h的降水概率预报可靠性高且预报技巧也高。
|
|
表 3 五个代表站概率回归和CMA集合预报BS评分与BSS评分 Table 3 The Brier score and Brier score skill of prediction of Logistic regression and T213-EPS at the five representative stations in the five areas |
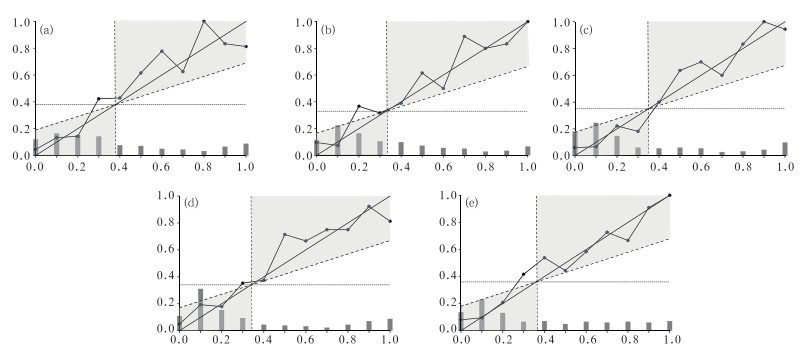
本节将以BSS特征图的方式更深入地分析BSS评分的意义,BSS特征图能更形象地说明集合预报系统的预报技巧和可靠性。该图是根据划分概率预报区间,将事件的相对频率与规定概率值下的预报概率进行对比得到。如图 3,折线实线上的点是将事件的相对频率与规定概率值下的预报概率进行对比得到的,表示在预报概率为f时,观测到降水事件出现的频率。BSS图中柱形代表规定概率的使用频率,规定概率使用频率的柱形图分布接近U型,说明此预报系统预报效果较好。下面分别给出五个代表站的24 h概率降水预报的BSS特征图,深入分析各区域各代表站点的概率预报特征和能力。
|
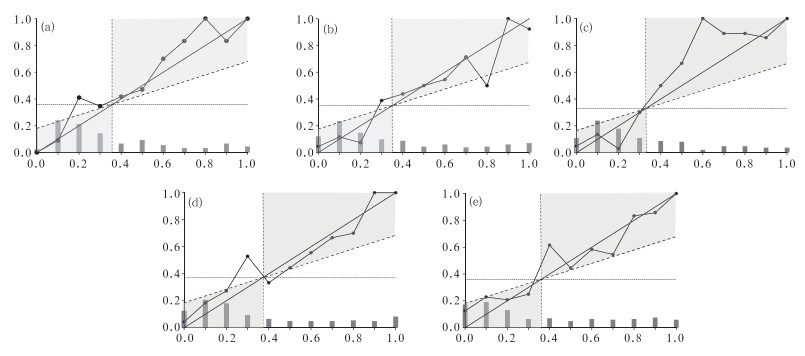
图 3 黄淮夏季降水五个分区代表站点技巧评分属性图 (横坐标表示预报概率,纵坐标表示观测的条件概率,垂直和水平虚线为无分辨性线,斜虚线为零分线,对角线为完美预报线,柱形代表规定概率的使用频率)(a)繁峙,(b)西平,(c)兖州,(d)正阳,(e)翼城 Fig. 3 Attributes diagrams for probabilistic prediction of precipitation at Fanshi (a), Xiping (b), Yanzhou (c), Zhengyang (d) and Yicheng (e), respectively (x-coordinate represents prediction probability, y-coordinate represents observation conditional probability, the dash line represents no resolution line, slanting dash line represents scoreless BSS, diagonal represents perfect prediction, and the histogram represents the frequency, resperctively) |
图 3a~3e分别是五个代表站点,即:繁峙、西平、兖州、正阳和翼城的预报技巧特征图。如图 3a所示,对于11个预报概率来讲,繁峙站有9个点预报概率在阴影内,只有预报概率是0.2和0.3时没有落在阴影里面,说明这两点无预报技巧,其他的预报概率均具有预报技巧,预报效果整体还是好于气候概率,尤其是在低概率事件时预报接近完美(靠近图 3a中的长虚线);概率值在0.5以后,折线在对角线上方,表示预报偏干,只有在概率为0.5和0.9时预报偏湿。西平站(图 3b)概率使用频率直方图大体呈现U型,这说明预报模型的概率分布较为合理。其中预报概率是0.3和0.8时落在阴影外面,说明这两点无预报技巧,其他的预报概率均在阴影内,说明该预报大部分具有预报技巧,预报效果整体还是好于气候概率,预报概率是0.2、0.6、0.8和1.0时预报偏湿,其余均偏干。兖州站(图 3c)所有折线上的点均落在阴影里面,预报概率值是0.2和0.6时,距离完美预报线的垂直距离较大,可靠性不好,但是概率是0.6使用频率很低,所以总体来讲该预报系统效果较好,其中预报概率是0.2和0.9时预报偏湿,其余均偏干;正阳站(图 3d)预报概率是0.3和0.4时没有落在阴影里面,说明这两点无预报技巧,其他的预报概率均在阴影内,且靠近完美预报线,说明该预报大部分具有预报技巧,且预报效果较好,预报概率值低于0.3时,折线在对角线上方,表示预报偏干,预报概率高于0.3时预报偏湿。翼城站(图 3e)折线上的点全部落在阴影内,预报概率为0.4和0.7时距离完美预报线的垂直距离较大,可靠性较差,其余预报概率均接近完美预报线,说明该站的预报模型预报效果较好,预报概率是0.0、0.2、0.4和0.8时预报偏干,其余各概率值预报偏湿。
3.4 试用效果检验将Logistic回归降水概率预报模型应用到近年(2012—2013年6—8月,由于2014年8月模式升级,故没有检验2014年的)业务试用中,得到的24 h降水概率预报与T213的集合预报24 h概率降水进行比较,表 4中列出了BS评分以及BSS评分。从表 4可以看出,本文Logistic本文概率回归的BS评分比CMA集合预报的BS评分值普遍低,且BS评分分值在0.19以下,说明本文概率回归的预报可靠性较CMA集合预报高。此外,从BSS的评分可以看出,本文概率回归预报的BSS评分均为正值,说明有预报技巧。而CMA集合预报的BSS评分均为负值,说明在本次检验中CMA集合预报的预报技巧低于检验样本的气候概率。总的来讲,本文Logistic回归降水概率预报模型在黄淮地区的预报效效果比CMA集合预报24 h的降水概率预报可靠性高且预报技巧也高。
|
|
表 4 2012—2013年五个代表站概率回归和CMA集合预报BS评分与BSS评分 Table 4 The Brier score and Brier score skill of prediction of Logistic regression and T213-EPS at the five representative stations over the five main areas during 2012-2013 |
在2012—2013年业务应用中,进一步分析各区域各代表站点的概率预报特征和能力,分别给出个五个代表站的24 h概率降水预报的特征图,如图 4a所示,对于11个预报概率来讲,繁峙站有10个点预报概率在阴影区内,只有预报概率是0.3时没有落在阴影区里面,说明这点无预报技巧,其他的预报概率均具有预报技巧,预报效果整体还是好于气候概率,尤其是在低概率事件时预报接近完美(靠近图 4a中的长虚线);概率值在0.5以后,折线在对角线上方,表示预报偏干,在概率为0.2、0.7、0.9和1.0时预报偏湿。西平站(图 4b)预报概率是0.2时落在阴影外面,说明这点无预报技巧,其他的预报概率均在阴影区内,说明该预报大部分具有预报技巧,预报效果整体还是好于气候概率,预报概率是0.5、0.7时预报偏干,其余均偏湿。兖州站(图 4c)所有折线上的点均落在阴影里面,该预报系统效果较好,其中预报概率是0.1、0.3、0.7和1.0时预报偏湿,其余均偏干;正阳站(图 4d)预报概率是0.3时没有落在阴影里面,说明这点无预报技巧,其他的预报概率均在阴影内,且除预报概率是0.5外,其他靠近完美预报线,说明该预报大部分具有预报技巧,且预报效果较好,预报概率是0.2、0.4、0.8和1.0时预报偏湿,其他偏湿。翼城站(图 4e)折线上的点除预报概率是0.3时,全部落在阴影内,且靠近完美预报线,说明该站的预报模型预报效果较好,预报概率是0.5和0.8时预报偏湿,其余各概率值预报偏干。
4 结论和讨论本文选取黄淮地区1961—2010年50年6—8月的日降水资料,将中国黄淮地区夏季日降水划分为五个夏季降水天气分区。在此基础上利用1999—2007年9年的资料建立了五个区域内代表站点的夏季日降水概率预报方程,并对2008—2009年6—8月预报进行了确定性和概率性预报检验,对2012—2013年6—8月进行了业务应用的检验。得出以下主要结论:
(1) 中国黄淮地区夏季日降水的REOF分析和t检验的方法得到黄淮地区五个夏季降水分区。这五个区域进行差异性t检验表明:五个区域均具有显著性差异,验证说明了区域划分的正确性。
(2) 分别建立了五个分区代表站的降水概率预报方程,对五个代表站日降水量的确定性预报检验表明:在检验时段内Logistic回归降水概率预报方程的TS评分要高于CFSv2模式和T213集合预报的集合平均,空报率也低于CFSv2模式和T213集合预报的集合平均,但是漏报率却略高,因此漏报率还有待改进。
(3) 对本文建立的五个代表站降水概率预报方程进行日降水量的概率预报检验表明:本文建立的预报方法的Brier评分的分值均较低,不超过0.2,其中兖州的BS评分值最小为0.13,其余站的BS评分均大大低于T213集合预报所得概率预报的Brier评分分值,说明本文的Logistic回归方程的概率预报可靠性高。Brier技巧评分BSS表明:Logistic回归降水概率预报方程各站的BSS技巧评分都大于0.0,说明各站的预报技巧高于检验样本气候概率的预报技巧,其中兖州站BSS评分最高为0.43,其余各站的BSS评分均高于T213集合预报的Brier技巧评分,2012—2013年6—8月的业务应用检验的结果与此结果类似。
(4) 任何一种评分方法都是有局限性的,一种检验评估方法只能是给出预报产品的一个或几个方面的信息。TS评分、Brier评分就是不同角度的预报检验方法。TS评分较适用于两分类预报结果的评估,即从某一天气现象是否出现来对预报结果进行评价。Brier评分是概率预报检验,Brier评分适用于多模式或多成员的概率预报检验,是从概率的角度分析捕捉到了某一天气现象,用0~1之间的一个数字表达该类天气现象发生的可能性。
需要指出的是,概率预报的检验要比确定性预报的检验在概念上复杂一些。比如,预报“明日降水的概率是0.7”,这样无论明日降水多大,或根本就没有降水,都不能说这个预报完全是对或是错。对于一个事件的概率,不是由一次试验能够确定的,而是要由很多次试验才能确定。为此,必须要有大量的预报及观测资料才能够做出可靠的预报检验。本文在对黄淮地区站点夏季降水概率预报模型进行检验的时候,分别用一和两年的资料进行检验发现:用时间长度为两年的资料检验该模型的预报效果要好于用时间长度是一年资料的检验结果。这说明增加检验样本的时间长度能够更好地体现一个预报模型的预报性能,检验样本时间越短偶然性越强。此外,本文建立的Logistic回归降水概率预报方程,仅是针对有无降水的概率预报,该方法和思路完全可以推广用于分等级的降水概率预报上,这对改善某些区域的降水概率预报,提供了有益的思路和有效的解决办法。
曹晓钟, 闵晶晶, 刘还珠, 等, 2008. 分类与集成方法在降雨预报中的应用[J]. 气象, 34(10): 3-11. DOI:10.7519/j.issn.1000-0526.2008.10.001 |
陈超辉, 王铁, 谭言科, 等, 2009. 多模式短期集合降水概率预报试验[J]. 南京气象学院学报, 32(2): 206-214. |
陈启槐, 葛军, 1999. TRP与Logit概率预报模式计算比较分析[J]. 气象科学, (3): 287-292. |
杜钧, 2002. 集合预报的现状和前景[J]. 应用气象学报, 13(1): 16-28. |
杜钧, 陈静, 2010. 天气预报的公众评价与发布形式的变革[J]. 气象, 36(1): 1-6. DOI:10.11676/qxxb2010.001 |
黄永新, 1997. 南宁市降水概率预报方法研究[J]. 广西气象, 18(S1): 49-52. |
闵晶晶, 孙景荣, 刘还珠, 等, 2010. 一种改进的BP算法及在降水预报中的应用[J]. 应用气象学报, 21(1): 55-62. DOI:10.11898/1001-7313.20100107 |
寗春蓉, 冯汉中, 2004. 利用卡尔曼滤波方法释用数值预报产品[J]. 四川气象, 24(2): 16-19. |
邵明轩, 刘凤辉, 程维中, 等, 2003. 用非线性多因子动态组合方法作降水概率预报[J]. 气象科技, 31(4): 206-210. |
汤银才, 2013. R语言与统计分析[M]. 北京: 高等教育出版社, 375.
|
田付友, 郑永光, 毛冬艳, 等, 2014. 基于Γ函数的暖季小时降水概率分布[J]. 气象, 40(7): 787-795. DOI:10.7519/j.issn.1000-0526.2014.07.002 |
王雨, 2004. 若干数值模式对2003年夏季青藏高原中南部降水预报检验[J]. 高原气象, 23(S1): 53-58. |
吴蓁, 吴富山, 孙景兰, 等, 1999. 郑州市降水概率预报[J]. 河南气象, 3: 11-12. |
曾晓青, 邵明轩, 王式功, 等, 2008. 基于交叉验证技术的KNN方法在降水预报中的试验[J]. 应用气象学报, 19(4): 471-478. DOI:10.11898/1001-7313.20080411 |
张诚忠, 2001. 不同因子处理方法对广西MOS方程降水预报准确率影响的试验[J]. 广西气象, 22(3): 24-25. |
张永领, 程炳岩, 丁裕国, 2003. 黄淮地区降水极值统计特征的研究[J]. 南京气象学院学报, 26(1): 70-75. |
张宇彤, 矫梅燕, 陈静, 2013. 基于模式先验信息的贝叶斯集合降水概率预报试验[J]. 气象, 39(10): 1233-1246. DOI:10.7519/j.issn.1000-0526.2013.10.001 |
赵翠光, 赵声蓉, 2011. 华北及周边地区夏季分区客观降水预报[J]. 应用气象学报, 22(5): 558-566. DOI:10.11898/1001-7313.20110505 |
赵琳娜, 刘琳, 刘莹, 等, 2015. 观测降水概率不确定性对集合预报概率Brier技巧评分结果的分析[J]. 气象, 41(6): 685-694. DOI:10.7519/j.issn.1000-0526.2015.06.003 |
赵琳娜, 吴昊, 田付友, 等, 2010. 基于TIGGE资料的流域概率性降水预报评估[J]. 气象, 36(7): 133-142. DOI:10.7519/j.issn.1000-0526.2010.07.020 |
赵声蓉, 赵翠光, 邵明轩, 2009. 事件概率回归估计与降水等级预报[J]. 应用气象学报, 20(5): 521-529. DOI:10.11898/1001-7313.20090502 |
周兵, 陆晨, 周小平, 1996. 北京地区夏季降水概率预报业务应用研究[J]. 气象, 22(1): 3-6. DOI:10.7519/j.issn.1000-0526.1996.01.001 |
Anderson J A, 1972. Separate sample logistic discrimination[J]. Biometrika, 59(1): 19-35. DOI:10.1093/biomet/59.1.19 |
Applequist S, Gahrs G E, Pfeffer R L, 2002. Comparison of methodologies for probabilistic quantitative precipitation forecasting[J]. Wea Forecasting, 17: 783-799. DOI:10.1175/1520-0434(2002)017<0783:COMFPQ>2.0.CO;2 |
Bocchieri J R, 1979. A new operational system for forecasting precipitation type[J]. Mon Wea Rev, 107: 639-649. |
Brier G W, 1950. Verification of forecasts expressed in terms of probability[J]. Mon Wea Rev, 78(1): 1-3. DOI:10.1175/1520-0493(1950)078<0001:VOFEIT>2.0.CO;2 |
Cox D R.1966.Some procedures associated with the logistic qualitative response curve//David F N. In Research Papers on Statistics:Festschrift for J Neyman.Chichester:Wiley, 55-71.
|
Day N E, Kerridge D F, 1967. A general maximum likelihood discriminant[J]. Biometrics, 23: 313-323. DOI:10.2307/2528164 |
Fritsch J M, House R A Jr, Adler R, et al, 1998. Quantitative precipitation forecasting:Report of the eighth prospectus development team, U S weather research program[J]. Bull Ame Meteor Soc, 79: 285-299. DOI:10.1175/1520-0477(1998)079<0285:QPFROT>2.0.CO;2 |
Hall T, Brooks H E, Doswell C A, 1999. Precipitation forecasting using an artificial neural network[J]. Wea Forecasting, 14: 109-118. DOI:10.1175/1520-0434(1999)014<0109:AOMTMN>2.0.CO;2 |
Krzysztofowicz R, 1993. Probabilistic quantitative precipitation forecasts for river basins[J]. Wea Forecasting, 8: 424-439. DOI:10.1175/1520-0434(1993)008<0424:PQPFFR>2.0.CO;2 |
Mullen S L, Buizza R, 2001. Quantitative precipitation forecasts over the United States by the ECMWF ensemble prediction system[J]. Mon Wea Rev, 129: 638-663. DOI:10.1175/1520-0493(2001)129<0638:QPFOTU>2.0.CO;2 |
Murphy A H, 1973. A new vector partition of the probability score[J]. J Appl Meteor, 12: 595-600. DOI:10.1175/1520-0450(1973)012<0595:ANVPOT>2.0.CO;2 |
Murphy A H, Martin E, 1987. On the relationship between the accuracy and value of forecasts in the cost-loss ratio situation[J]. Wea Forecasting, 2: 243-251. DOI:10.1175/1520-0434(1987)002<0243:OTRBTA>2.0.CO;2 |
North G R, Bell T L, Cahalan R F, et al, 1982. Sampling errors in the estimation of empirical orthogonal functions[J]. Mon Wea Rev, 110(7): 699-706. DOI:10.1175/1520-0493(1982)110<0699:SEITEO>2.0.CO;2 |
Sanders F, 1986. Trends in skill of Boston forests made at MIT1966~84[J]. Bull Amer Meteor Soc, 67: 170-176. |
Walker S H, Duncan D B, 1967. Estimation of the probability of an event as a function of several independent variables[J]. Biometrika, 54: 167-179. DOI:10.1093/biomet/54.1-2.167 |
 2015, Vol. 41
2015, Vol. 41