引言

风资料在风能资源评估(李艳等，2007)、城市建筑、桥梁水库建设、市政规划设计等社会各行业应用非常广泛。由于风向风速传感器安装高度较高，一般在10 m以上，如安装在铁塔上其高度可达100 m甚至更高，这样给仪器的常规维护带来较大困难，由此使得仪器故障不能及时得到发现、诊断和排除，从而导致观测数据的质量受到很大影响。

针对气象观测数据进行质量控制，其方法较多，主要有气候极值范围检查、内部一致性检查、时间一致性检查、空间一致性检查等(李志鹏等，2012；王海军等，2007；王新华等，2006)。国外有学者对于风资料的质量控制方法作过研究(DeGaetano, 1997；Jiménez et al，2010)，如DeGaetano(1997)对美国NCDC的逐时风资料进行了质量控制，但我国在该方面还没有学者进行过系统研究。同时上述这些质量控制方法，主要研究检测疑误数据及其处理方法，并未涉及这些疑误数据产生的原因(如仪器性能下降)，也无法检测出部分风向方位缺失等故障导致的数据质量问题。

在我国地面气象探测系统中，风向传感器发生故障导致观测数据质量下降现象时有发生(刘军等，2006；杨丽中等，2010；周晓香等，2009)。某一范围内的风向缺失，即由于仪器故障或受外力影响，导致较长时间内(如1~2个月)某一范围内(如180°~360°)的风向一直不出现。本文在不对观测仪器进行硬件检测的情况下，利用观测资料，对某区间内风向缺失情况进行检测，为设备保障技术人员提供较为准确的参考信息，以提高测风仪器的可用性，从而提升观测数据质量。

1 数据

本文所使用资料为2009—2011年3年自动站风观测数据，资料的台站为全国国家级自动气象站共2420站，要素为逐小时极大风速的风向(简称极大风向)、瞬时风速的风向(简称瞬时风向)、2 min平均风向资料。数据来源于国家气象信息中心。

2 风向传感器故障后数据表现特征

按照自动站风向传感器测量原理，同时结合实际业务运行维护情况，发现风向传感器由于仪器故障导致格雷码展现形式与实际风向不符(简称格雷码失效故障)的情况最多。当发生格雷码失效故障时，7位格雷码中有一位或多位并不随着风向的变化而变化，而是一直处于接通或断开状态，本文称为“恒为1”或“恒为0”状态。下面根据格雷码编码原理，分析故障发生时风向观测数据的表现特征。

风向传感器为单翼风标，采用光电转换即格雷码盘来传送和指示风向标所在方位。格雷码盘将风向标轴的转动角度的度数变换成一个二进制的数字信号。格雷码盘是由等分的同心圆组成，由内到外分别做2⁰、2¹、…、2ⁿ等份，相邻两份做透光和不透光处理，在每一个同心圆上放置一个红外发光管，n个发光管排列在同一个半径上。在码盘下方放置与红外光源一一对应的光电接收管，作为转换器，当光通过码盘的透明部分时，光电接收管接收到的信号为“1”，当光通过码盘的不透明部分时，光电接收管接收到的信号为“0”，通过光电转换线路，把光信号转换为电信号，输入到指示、记录装置。风标转动时，带动格雷码盘转动，就形成n位格雷码信号，实现风向与n位格雷码的转换，每一个码表示一个风向，风向的分辨率为360°/2ⁿ, 若采用7位格雷码，则分辨率为360°/2ⁿ=2.8°。

当7位格雷码中有一位有故障时，就会导致采集的风向数据发生失真。为分析各位格雷码输出故障时，输出风向的偏差情况，本文依据格雷码编码原则，统计了当实际风向从0°~360°变化时，如某一格雷码失效故障(即该位格雷码恒输出0或1) 所输出的风向。结果表明当格雷码的某一位“恒为0或1”时，会导致某一个或多个范围内风向不会出现(表 1)。如当格雷码第七位“恒为0”时，风向在180°~ 360°不会出现。记为D_{0, 7}∈(180°, 360°)，D_{0, 5}∈{(45°, 135°), (225°, 315°)}。

当格雷码位i为1和2时，表 1中未列出其缺失区间。表中D_{0, i}、D_{1, i}分别表示格雷码第i位发生恒为0、1失效故障时不会出现的风向区间。由表 1数据可知，当某一位格雷码失效时，会导致一个或多个区间的风向不会出现，但这些不会出现的区间的累积角度为整个角度区间的一半，即180°。

3 格雷码盘故障检测原理与方法

由前文分析可知，当格雷码盘的某位格雷码失效(恒为0或1) 时，某一固定区间(该固定区间由一个或多个区间组成，下文统称区间)的风向不会出现，这样可统计一个时间段内该区间内风向出现次数与实际总次数的比值来检测，如果该比值为0(或很小)，且持续时间较长，则可判定该位格雷码发生了故障。为此有如下定义：

$ {P_{0, \mathit{i}}} = \frac{{{n_{0, \mathit{i}}}}}{\mathit{N}} $

(1)

$ {P_{1, \mathit{i}}} = \frac{{{n_{1, \mathit{i}}}}}{\mathit{N}} $

(2)

式中，n_{0, i}为某站一定时段内(如一旬)风向在D_{0, i}范围内实际出现次数，N为该时段内总次数。n_{1, i}为一定时段内(如一旬)风向在D_{1, i}范围内实际出现次数。i取值1~7，表示格雷码位序。根据式(1) 和(2)，P_{0, i}和P_{1, i}取值在0~1。

按照定义，P_{0, i}为某站某一个时间段内风向出现在D_{0, i}区间内次数与该时段内所有风向总次数的比值(简称风向区间比值)，根据表 1，D_{0, i}的风向累积区间为180°，所以对于一个风向较为均匀分布的台站而言，如风向传感器运行正常，则P_{0, i}一般在0.5左右。同样P_{1, i}也应在0.5左右。

如风向传感器的第i位格雷码失效(恒为0) 时，由于风向在D_{0, i}区间不会出现，即n_{0, i}=0，因此P_{0, i}=0。为此可根据风向区间比值P_{0, i}的大小来判断风向传感器的第i位格雷码是否发生失效故障(恒为0)。

由于在气象业务中能够获取的是一定时间范围内的平均风向，即使发生第i位格雷码失效故障(恒为0) 时，实际的观测风向数据在区间D_{0, i}也有可能出现。如第三位格雷码失效故障时，虽然采集器在数据采样时不会记录到11°~32°区间的风向，但如果在计算的平均时间内，既出现了小于11°(如10°)的风向，又出现了大于32°(如34°)的风向，则该时间的平均风向数据就会出现在11°~32°区间内。所以在检测格雷码失效故障时，不能选择平均时间较长的风向观测要素，如2、10 min的平均风速的风向。为此选择平均时间为3 s的逐小时极大风向和瞬时风向。由于平均的时间较短(为3 s)，这样当发生格雷码故障时，记录到的风向观测数据在区间D_{0, i}的概率就会小很多。为此本文取P_{0, i}小于某一个阈值时，就判断格雷码发生失效故障，而不是以P_{0, i}=0作为判据。

4 风向区间比值分析及格雷码失效判定方法 4.1 风向区间比值频率分布

根据式(1) 和(2)，计算出各位格雷码失效时，各旬极大风向和瞬时风向的区间比值，并分析其频率分布。

4.1.1 风向区间比值分布

经统计，河南南阳站极大风向2009年年平均区间比值P_{0, i}分别依次(i从1到7) 为0.49、0.45、0.45、0.53、0.53、0.45和0.35，该站极大风向的逐旬区间比值如图 1所示，其中区间比值P_{0, i}、P_{0, 3}、P_{0, 5}的逐旬变化基本上在0.5上下窄幅变化，而P_0.7变化幅度较大。

为分析风向区间比值在全国的分布情况，计算了全国2009—2011年2420站3年极大风向平均区间比值，统计了平均区间比值(3年平均)在0.3~0.7范围台站数在所有台站中所占的比例(表 2)。

由表 2可知3年年平均区间比值P_{0, i}在0.3~0.7的台站超过了80%，其中格雷码位序在1~4的在90%以上。由此可见，大部分台站的极大风向区间比值P_{0, i}和P_{1, i}在0.3~0.7，瞬时风向区间比值也有相似结果，不再赘述。

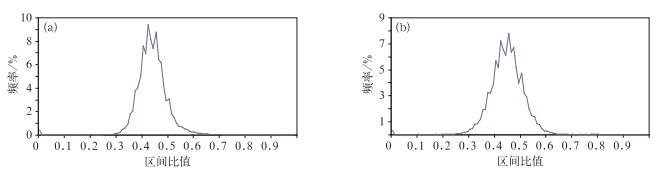
4.1.2 风向区间比值频率分布

计算了全国2009—2011年2420站逐旬的极大风向和瞬时风向各格雷码风向区间比值，并统计了区间比值的频率分布(图 2)。由图 2可知，旬区间比值P_{0, 2}在0.3~0.7范围的比例超过98%。

4.2 格雷码失效判定标准

通过单站逐旬风向区间比值以及全国逐旬风向区间比值频率的系统分析，各站旬风向区间比值分布尽管在不同的格雷码位序以及极大与瞬时风向有一定差异，但总体上来说分布较为一致(图 2)，为分析问题简便起见，本文统一选定旬区间比值小于0.05时，格雷码发生了失效故障。为进一步分析该阈值的有效性，统计了旬极大与瞬时风向区间比值小于0.05的百分比(表 3)。

综上所述，格雷码失效故障判定方法是：当某站连续3旬的极大风向和瞬时风向的区间比值P_{0, i}均小于0.05时，就称该站的风向传感器格雷码第i位发生了恒为0失效故障。恒为1失效故障的判定标准与此相同。

5 检测结果分析及影响评估 5.1 格雷码失效故障检测结果分析

根据前文格雷码故障的检测方法，统计了全国2009—2011年2420站格雷码故障的台站数。

由表 4可知，格雷码为2~7位出现故障的台站在全国所占比例为0.4%~0.8%(恒为0与1之和)，但格雷码第一位出现失效的比例为2.6%，远远高于其他位数。为分析第一位出现故障的比例高的原因是否与统计方法有关，通过进一步分析，发现格雷码第一位出现失效的旬区间比值有超过1/3等于0，由此表明即使风向区间比值阈值调整为0.0，格雷码第一位出现失效的台站每年超过0.8%，也高于其他位序格雷码失效的比例(区间比值阈值为0.05)。

此外，由表 4可知格雷码出现恒为0的故障站数比恒为1多，具体原因可能是导致恒为0的较比恒为1的仪器故障更易出现，比如遭受雷击、断电等情况导致仪器故障。

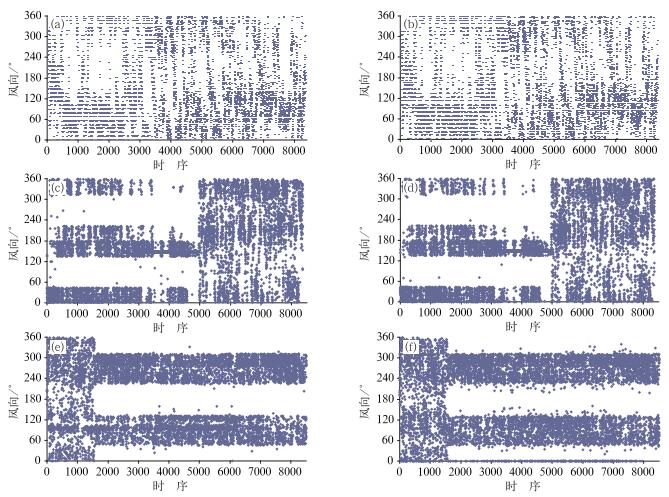
下面通过3个站检测结果说明格雷码失效时风向数据的分布情况。图 3a、3b为丹阳站第一位格雷码失效(恒为0) 示意图(图中时序为距第一个数据的小时数)。该站从2009年7月上旬到11月中旬极大风向和瞬时风向区间比值均小于0.05。从2009年11月下旬开始，两个风向区间比值恢复正常变化范围，在0.5附近波动(图略)，对应图 3a、3b在2009年11月下旬以前的风向数据呈“带状”分布，从0°~360°范围内有32个小区间没有(或少量)风向出现。但在2009年11月下旬以后，风向数据的分布较为均匀，没有之前的明显“带状”分布情况。

图 3c、3d为兴城站第五位格雷码失效(恒为0) 示意图，格雷码失效起止时间为2010年1月上旬到8月上旬；图 3e、3f为朔州站第五位格雷码失效(恒为1) 示意图，格雷码失效起止时间为2010年3月上旬至12月下旬。通过图 3可知，当发生格雷码失效故障时，风向数据呈明显“带状”分布。

5.2 极大、瞬时和2 min风向区间比值关系

为比较极大、瞬时和2 min风向不同要素区间比值的关系，本文统计了逐旬极大风向的区间比值小于0.05时，所对应的逐旬瞬时风向以及2 min平均风向区间比值小于0.05比例(表 5)。

当极大风向的区间比值小于0.05时，对应的瞬时风向比值小于0.05的比例超过了91%，说明极大风向和瞬时风向的区间比值有很好的相关性。说明极大和瞬时风向区间比值小于0.05不是一个偶然事件，一定有某一个事件导致极大和瞬时风向区间比值同时小于0.05，该事件就是格雷码失效故障。反过来说，利用极大和瞬时风向资料可分辨出格雷码失效故障。

由表可知，当极大风向的区间比值小于0.05时，2 min平均风向在格雷码位序在1~4范围内比例不到10%。由此表明，当极大和瞬时风向的区间比值小于0.05时，即发生格雷码失效现象时，所对应的2 min平均风向区间比值可能远远大于阈值0.05，所以采用2 min平均风向来检测格雷码失效能力有限，只能较好地检测格雷码位序为6、7的失效故障，而对于雷码位序在4及以下的失效故障无能为力。

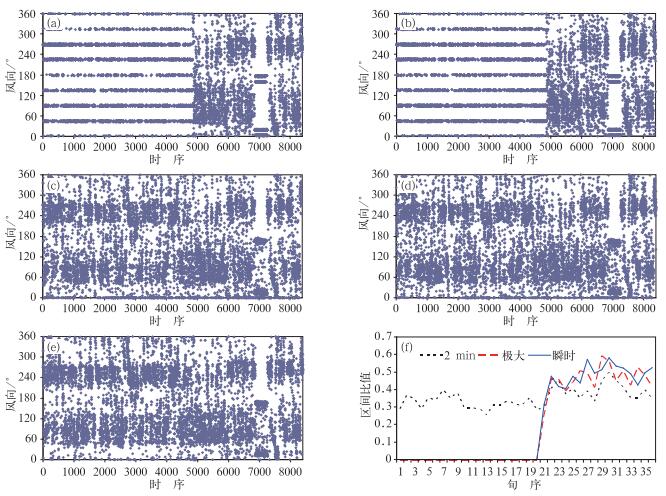
为进一步说明不同时间尺度的风向资料在发生格雷码失效时表现情况，本文制作了逐时极大、瞬时、2 min、10 min、最大风速的风向的分布情况(图 4)。由图 4可知，山东沂源站2009年1月上旬至7月中旬发生了格雷码第三位失效(恒为0) 故障。但只有极大、瞬时风向的分布(图 4a、4b)可看出非常明显的“带状”分布，而2 min、10 min、最大风速的风向(图 4c、4e)在该时段的分布较为均匀。图 4f 2 min风向在格雷码失效期间的旬风向区间比值在0.25~0.40，由此进一步说明2 min等较长时间的平均风向在检测格雷码失效时的缺陷。

5.3 影响评估分析

当格雷码故障时，会导致某些范围的风向不出现，而其他方向出现次数出现频率比实际情况多，从而导致风向的分布与实际出现偏差，甚至出现完全与实际情况相反的情况。下面通过模拟当某位格雷码失效后，年风向频率、风向平均值与标准差与观测资料的差异来分析其影响。

5.3.1 年风向频率分布

以武汉2009年极大风向资料为例，通过风向玫瑰图分析格雷码失效前后年风向频率分布差异。

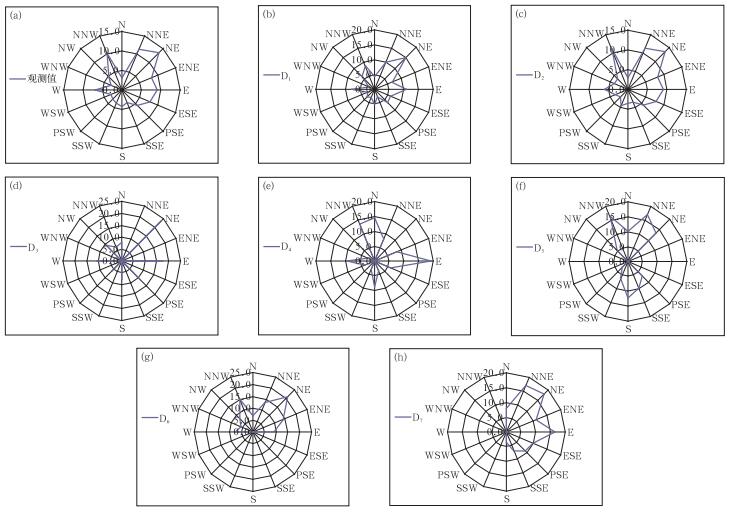
由图 5可知，当第一、二位格雷码发生失效故障(恒为0) 时，各个方位的风向频率和原始观测值虽有差异，但并不很大。然而第三~七位故障时，分别有7、4、6、7、7个方位的频率为0，导致风向频率的主导风向完全发生了改变。需要指出的是，该模拟是针对的极大风速的风向理想情况，实际发生故障时，由于在3 s风向平均，可能会略有差异。

5.3.2 风向平均值和标准差

在大气边界层和大气扩散以及大气污染研究中，常会用到平均风向和标准差参量(邱传涛等，1997；姚增权等，1990)。下面分析格雷码发生失效故障时，平均风向和标准差的变化情况。由于风向存在过零问题，对于风向序列平均值和方差的计算不能采用通常算法。本文采用式(3) 和(4) 计算风向的平均值和标准差。

$ \bar \theta = {\rm{arctan}}\frac{{{M_s}}}{{{\mathit{M}_\mathit{c}}}} $

(3)

$ \sigma _\theta ^2 = \frac{1}{N}\sum\limits_{i = 1}^\mathit{N} {\Delta _i^2 - \left({\frac{1}{N}\sum\limits_{i = 1}^\mathit{N} {{\Delta _i}} } \right)} $

(4)

式中，$ {\mathit{M}_\mathit{s}} = \frac{1}{N}\sum\limits_{i = 1}^\mathit{N} {{\rm{sin}}{\theta _\mathit{i}}}, $$ {\mathit{M}_\mathit{c}} = \frac{1}{N}\sum\limits_{i = 1}^\mathit{N} {{\rm{cos}}{\theta _\mathit{i}}} 。$式(4) 中Δ_i是这样定义的, 使|Δ_i|是|θ_i-θ|和2π|θ_i-θ|中的较小者。θ为平均风向，θ_i为各逐时风向，σ_θ为风向标准差。

本文以新疆乌恰站2009年极大风向为例，说明模拟前后平均风向和风向标准差的变化差异(表 6)。表 6和图 5中D₁~D₇表示模拟第一至七位格雷码失效的数据。

通过表 5可知，平均风向在D₁、D₂、D₃时，一般相差不大，最大在10°左右，但在D₄、D₅、D₆、D₇时，相差就非常大，甚至超过150°。标准差平均风向在D₁、D₂、D₃时，一般相差不大；在D₄、D₅与实际的变化趋势呈现多样化变化，有的比实际值大，有的小，有的相当；在D₆、D₇时，标准差明显比实际值偏小。由此表明，当雷码发生失效故障时，平均风向和标准差的变化较大。

上述结论虽然是根据武汉和乌恰2个站2009年分析结果，该结论也适用于其他台站其他年份资料。

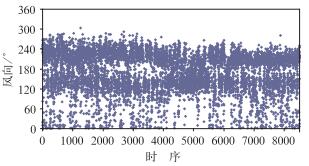
6 任意区间风向缺失检测

前文讨论了格雷码失效故障的检测方法，其实在自动气象站的实际运行过程中，也存在由于结冰或堵塞等原因，导致风向标只在某个范围内转动，使得风向数据在该范围外无法出现情况，从而导致某个区间的风向缺失，但该区间和格雷码失效后风向区间缺失不一样，其大小不固定且起始位置随机。为检测该现象，本文仿照格雷码故障检测原理，设计了检测方法。基本原理是给定一个方向范围，如100°~145°，然后检测一定时间(1旬)的极大风速的风向和瞬时风向在该范围内出现的频率，如频率很小且持续时间较长(超过3旬)，就认为该站的风向在该范围内出现了缺失现象。为此设计了任意区间的风向缺失检测方法，并对全国2009—2011年的风向资料进行了检测。如图 6大方站在2010年极大风向在270°~360°范围内极少出现，由此可判断该站的风向资料在该范围内发生了缺失现象。由于篇幅所限，具体方法与检测结果不再赘述。

7 结论

利用全国2009—2011年3年2420个国家站逐时风向资料，对风向在某区间内缺失的情况进行了检测。结论如下：

(1) 利用逐时的极大风速的风向和瞬时风速的风向资料，可检测风向传感器的格雷码故障情况，也可检测任意区间风向缺失。

(2) 格雷码为2~7位出现失效故障的台站在全国所占比例为0.4%~0.8%，但格雷码第一位出现失效故障的比例达2.6%，其中格雷码出现恒为0的故障站数比恒为1多。

(3) 通过模拟，当格雷码失效时，导致风向频率分布、平均风向及风向标准差与实际观测值差异较大，当失效格雷码为第四至七位时，数据差异更大。