引言

由于冰雹单体生成的宏观条件、生成源地及移动路径具有明显的局地特征，它不仅决定于大气环境条件，而且受地形的影响很大，因此冰雹预警一直是临近预报的重点和难点。对强对流天气进行探测和预警是多普勒天气雷达应用的主要领域，CINRAD WSR-98D SA/SB v 10中的中尺度天气系统及灾害性天气识别产品包括风暴追踪信息(Storm Track Information，STI)、冰雹指数(Hail Index，HI)、中气旋(Mesocyclone，M)和龙卷涡旋特征(Tornadic Vortex Signature，TVS)，由于它们能快速、定量识别强对流天气主要特征而受到预报员的认可(Lee等，2000)。在HI产品的应用上，我国业务人员已积累了一些相关经验。如，HI产品往往高估冰雹发生的可能(吴林林等，2014)，尤其是在夏季可能无法区分强降水和冰雹(邵玲玲等，2007)。可以利用多普勒雷达垂直累积液态水(Vertically Integrated Liquid，VIL)产品或VIL密度作为判断冰雹是否能形成的补充阈值使用等(刁秀广等, 2008；张崇莉等, 2012；段鹤等, 2014)。

对HI产品的应用要建立在对冰雹算法的原理和特点有深入了解之上。本文首先回顾多普勒雷达探测冰雹的算法发展历程，给出当前算法高估冰雹发生概率及冰雹尺寸的原因。为降低虚警率，本文给出了除三体散射(Three-Body Scatter Spike，TBSS)、高VIL等特征以外的一个定量指标，即-20℃层等高平面(Constant Altitude Plan Position Indicator，CAPPI)产品上55 dBz的面积范围阈值。

1 多普勒雷达探测冰雹的算法发展

目前我国CINRAD WSR-98D SA/SB v 10算法软件基本上与美国WSR-88D build 10算法软件一致。该版本中的冰雹算法称为冰雹探测算法(Hail Detection Algorithm，HDA)。考虑到算法的改进有其延续性，因此有必要了解前期的冰雹算法。

1.1 前期冰雹算法及评估

WSR-88D的前期冰雹算法是建立在由风暴序列算法识别出风暴单体的基础上，再根据相应预报因子累积权重判断风暴单体是否有可能降雹。

该算法是由Petrocchi(1982)开发的，是以美国俄克拉荷马地区典型超级单体雹暴特征为基础建立的(Lemon, 1978)。算法使用由风暴序列算法得到的风暴单体特征数据来检验7个冰雹预报因子(Winston，1988)。表 1为Petrocchi定义的冰雹预报因子及其相应权重。

表 1中的2D分量指某仰角上方位角和距离相距较近的≥30 dBz回波所组成的区域。算法的冰雹预报因子充分考虑了人工雹暴识别中的“高悬的强回波”、“弱回波区或有界弱回波”等特征结构，并对它们赋予不同的权重值。在冰雹预报因子检测完成后，根据所得的累积权重是否超过阈值，判定风暴单体降雹为四种可能之一：肯定、可能、否定或未知(资料不足)。

最初的检验表明该算法效果较好(Petrocchi，1982；Smart et al，1985)，其后Winston(1988)使用美国科罗拉多高原地区实际冰雹资料进行检验，认为算法效果较差。

由表 1可看出，Petrocchi的冰雹预报因子针对的是俄克拉荷马地区典型降雹单体-超级单体风暴，算法除要求风暴单体最大反射率因子高度比较高外，还强调了超级单体风暴的弱回波区和回波悬垂结构。而科罗拉多高原地区降雹可能主要由非超级单体风暴引起，其最大反射率及反射率高度能满足阈值，但弱回波区和回波悬垂结构不一定能满足阈值，这就会导致算法在科罗拉多高原地区应用效果较差。

1.2 HDA算法及评估

WSR-88D build 9对初期的冰雹算法进行了改进，并延续使用至build 10。由于冰雹探测与风暴单体的识别密切相关，故build 9同时将之前的风暴序列算法改进为风暴单体识别和跟踪算法(Storm Cell Identification and Tracking，SCIT)(Johnson et al，1998)。

改进后的冰雹算法称为冰雹探测算法(Hail Detection Algorithm，HDA)，它是将SCIT算法探测到的风暴单体“段”组合成风暴2D分量，每个2D分量的高度和最大反射率用于产生单体的垂直反射率廓线，HDA则用垂直反射率分布来确定单体的冰雹潜势。由HDA算法给出的HI产品有以下三部分内容：冰雹概率(Probability Of Hail, POH)、强冰雹概率(Probability Of Severe Hail，POSH)及最大预期冰雹尺寸(Maximum Expected Hail Size, MEHS)。

1.2.1 HDA算法

(1) 冰雹概率(POH)

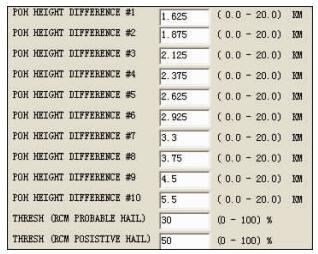
在20世纪70年代初位于南非内尔斯普雷特的防雹试验中，发现可以根据云顶高度超过12 km、最大反射率超过45 dBz来进行消雹。同时又注意到在45 dBz不超过7.5 km时，很少有地面冰雹报告，因此认为45 dBz高度是否超过7.5 km也可以用作是否进行消雹的一个判别标准(Mather et al，1976)。在1972—1974年美国科罗拉多东北部进行的消雹试验中，发现有“冻结粒子”(即小于0℃)胚胎的风暴更容易产生冰雹(Foote et al, 1979)。在此基础上，Waldvogel等(1979)分析了前苏联1976—1981年在瑞士中部进行的消雹试验资料，发现前苏联当时使用的3 cm雷达所观测到的45 dBz高度与0℃层高度之间的差与地面降雹概率之间有简单的对应关系(图 1)，此即为目前HDA算法中所使用的POH关系式。图 1为我国CINRAD WSR-98D SA/SB多普勒雷达产品生成(Radar Product Generator，RPG)中POH的缺省参数值。例，45 dBz高度与0℃层高度之间的差≥2.925 km时，对应POH高度差为#6，即地面降雹概率为60%。

(2) 强冰雹概率(POSH)

首先将10 cm雷达观测的反射率与地面降雹联系起来的是Geotis(1963)，他发现“如果55 dBz的回波持续数分钟，则地面一定降雹”。Waldvogel等(1977)得到了类似的结论，即用时间积分55 dBz的区域来区分降雹和不降雹单体，当其值超过100 km²时，单体为降雹单体。但上两个判据并不能给出冰雹强度与反射率之间的定量关系。

类似于多普勒雷达降水算法中的Z-R关系，在假设瑞利散射及冰雹粒谱分布为指数分布时，冰雹动能通量(Ė)与反射率因子(Z)之间的关系可写为(Waldvogel et al，1978)：

$ \mathit{\dot E = b}{\rm{1}}{{\rm{0}}^{{\rm{ - 6}}}}{\mathit{Z}^\beta } $

(1)

式(1) 中

$ Z = \int_0^\infty {\mathit{N}(\mathit{D}){\mathit{D}^6}{\rm{d}}\mathit{D}\;\;\;[{\rm{m}}{{\rm{m}}^6} \cdot {{\rm{m}}^{ - 3}}]} $

(2)

$ \dot E\frac{{{\rm{ }}\mathit{\pi }\rho }}{{12 \times {{10}^6}}}\int_0^\infty {N(D){D^3}{v^{\rm{3}}}{\rm{d}}D\;\;\;[{\rm{J}} \cdot {{\rm{m}}^{{\rm{ - 2}}}} \cdot {{\rm{s}}^{ - 1}}]} $

(3)

式中，b、β为系数，D为雹粒直径；N(D)为冰雹粒谱分布；ρ为雹粒的密度，取0.9 g·cm^-3；v为雹粒的下落速度，假设v=v₀D^0.5, v₀=4.41 m·s^-1。Waldvogel使用6个强雹暴(1973年7月6日；1975年6月27日a；1975年6月27日b；1975年7月11日a；1975年7月11日b；1976年5月19日)观测的175个雹粒谱分布，点绘在Z-Ė图上并作拟合，给出半经验半理论的Z-Ė关系式为：

$ \mathit{\dot E} = 5.0 \times {10^{ - 6}}{\mathit{Z}^{{\rm{0}}{\rm{.84}}}} $

(4)

HDA算法中对式(4) 作了两个改变。第一个改变是将Z的单位由mm⁶·m^-3改成dBz，并考虑反射率大小的权重因子，将式(4) 改写为：

$ \mathit{\dot E} = 5.0 \times {10^{ - 6}}\mathit{W}{\rm{(}}\mathit{z}{\rm{)1}}{{\rm{0}}^{{\rm{0}}{\rm{.084}}\mathit{Z}}} $

(5)

式中

$ \mathit{W}(\mathit{Z}) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{Z} \le 40\;{\rm{dBz}}\\ {\rm{0}}{\rm{.1(}}\mathit{Z}{\rm{ - 40)}}\;{\rm{40}}\;{\rm{dBz < }}\mathit{Z < }{\rm{50}}\;{\rm{dBz}}\\ {\rm{1}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{Z} \ge 50\;{\rm{dBz}} \end{array} \right. $

(6)

通过W(Z)权重函数过滤掉40 dBz以下的值(即认为是液态水)，大于50 dBz的值认为是冰雹粒子，40~50 dBz认为是液态水和冰雹粒子的转换区。

由于雹粒增长发生在0℃以上，而强雹粒子增长在接近-20℃层及以上更冷的区域(English，1973；Browning，1977；Nelson，1983；Miller et al，1988)。因此，对式(4) 的第二个改变是引入0℃和-20℃层高度的权重函数：

$ {\mathit{W}_{\mathit{T}}}(\mathit{H}) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{H} \le {H_0}\\ \frac{{H - {H_0}}}{{{H_{ - 20}} - {H_0}}}\;\;\;{H_0} < \mathit{H < }{\mathit{H}_{{\rm{ - 20}}}}\\ {\rm{1}}\;\;\;\;\;\;\;\;\;\;\;\;\mathit{H} \ge {\mathit{H}_{{\rm{ - 20}}}} \end{array} \right. $

(7)

式中, H是相对地面的高度，H₀是0℃层高度，H_-20是-20℃层高度。

综合上两点改变，定义强冰雹指数为：

$ \mathit{SHI = }{\rm{0}}{\rm{.1}}\int_{{H_0}}^{{H_T}} {{\mathit{W}_\mathit{T}}(\mathit{H})} \mathit{\dot E}{\rm{d}}\mathit{H} $

(8)

式中，积分上限H_T是SCIT算法得到的风暴单体顶的高度。对强冰雹指数SHI要注意到：(1) SHI中每个仰角的Ė是用SCIT算法识别的风暴单体2D分量的最大反射率因子计算的；(2) SHI是累积0℃层高度以上直至风暴顶(注：≥30 dBz的2D分量最高高度)之间各仰角的冰雹动能通量。由式(6) 和式(7) 可看出，实际累积的是0℃层到≥40 dBz的2D分量最高高度之间各仰角的冰雹动能通量。因此，2D分量最大反射率越大，且越接近或超过-20℃层高度，则SHI值越大，降强雹的可能也愈大。

SHI有助于判断SCIT识别的单体是否会降强雹，但冰雹在大于0℃的环境下会发生融化，因此融化层到地面的高度也可以作为判断强雹是否产生的条件之一。Witt等(1998)使用俄克拉荷马和佛罗里达的10个强雹个例(除1个个例是1989年外，其余都是1992年春季和夏季的；其中有8个个例观测到有直径＞1.9 cm，最大达10.2 cm的强雹；有2个个例没有冰雹大小记录)，通过将融化层高度和SHI值作点聚并拟合，给出了考虑冰雹通过暖湿环境层的警报阈值为：

$ \mathit{WT = }{\rm{57}}{\rm{.5}}{\mathit{H}_{\rm{0}}} - 121 $

(9)

式中，WT是SHI达到的警报阈值，即SHI达到此值，单体附近一定空间范围和时间区间内可能有强雹，H₀(km)是0℃层高度(注意：尽管冰雹的融化层高度更接近于湿球0℃层高度(俞小鼎等，2014)，但这里仍用的是干球0℃层高度)。例，式(9) 中0℃层高度为3 km时，WT为51.5 J·m^-1·s^-1，即此时SHI达到51.5 J·m^-1·s^-1，则可能降强雹；0℃层高度为4 km时，WT为109 J·m^-1·s^-1，即此时SHI需达到109 J·m^-1·s^-1，才可能降强雹。

为更加定量化，用有最高和最低0℃层高度的两个风暴得到简单的概率函数，再用所有10个风暴来确定概率的刻度，得到了POSH概率函数：

$ \mathit{POSH} = 29{\rm{ln}}\left({\frac{{\mathit{SHI}}}{{\mathit{WT}}}} \right) + 50 $

(10)

式中，POSH为降强雹的概率。由式(10) 可见，SHI达到WT值时，POSH概率为50%，这也是通常将POSH≥50%作为强雹预警阈值的原因。

图 2为我国多普勒雷达RPG中POSH使用的缺省参数值，它包括了式(5)~式(10) 中的所有系数值。例，图 2中最后两行的57.5和-121对应的则是式(9) 右侧的两个系数。

(3) 最大预期冰雹尺寸(MEHS)

SHI也用来对最大预期冰雹尺寸(Maximum Expected Hail Size, MEHS)进行估计。Witt等(1998)使用上述8个有冰雹尺寸观测记录的数据及1992年6月18日Twim Lakes冰雹数据(9个个例共有147个强冰雹尺寸观测记录)，建立了最大预期冰雹尺寸与SHI之间的拟合关系式：

$ \mathit{MEHS = }{\rm{2}}{\rm{.54(}}\mathit{SHI}{{\rm{)}}^{{\rm{0}}{\rm{.5}}}} $

(11)

式中MEHS单位为mm。之所以称为最大预期冰雹尺寸，是因为由点聚图(纵坐标为观测到的冰雹尺寸，横坐标为SHI值)得到式(11) 时，大部分观测记录是位于拟合线以下的，即式(11) 本身就高估了冰雹尺寸。

1.2.2 HDA算法评估

Witt等(1998)利用1992、1993年夏季在科罗拉多东北部进行的冰雹试验资料对POH进行检验，发现使用POH≥50%作为冰雹预警阈值，则命中率POD=92%，虚警率FAR=4%，临界成功指数CSI=88%。利用美国不同地点的30个个例资料(1992—1995年)对POSH进行检验，发现使用POSH≥50%作为强雹预警阈值，在南部平原地区效果较好；在美国北部地区和山区，有较大的过高估计强雹概率误差。这一方面与冰雹气候分布特征有关，因为大平原地区更容易有强雹；另一方面可能与美国南部有更密的观测网有关。

由于缺乏可靠的地面最大冰雹尺寸观测资料，很难对MEHS进行检验和评估。

2 CINDAD-98D冰雹产品业务应用讨论

初期的冰雹算法关注的是超级单体回波特征结构的识别方法，如弱回波区和回波悬垂结构等。HDA算法不但考虑了不同仰角高度上的最大反射率值，还由冰雹形成物理过程考虑了强雹与环境温度的关系。如，对POSH而言，首先是建立某仰角高度上冰雹动能通量与反射率之间的统计关系；综合考虑环境0℃和-20℃层高度及反射率大小，得到强冰雹指数SHI；考虑强雹在大于0℃层环境中的融化得到SHI的警报阈值；最后得到POSH。美国165部WSR-88D雷达的HDA算法中，全部预置的是上述算法参数。我国最终将布设216部多普勒天气雷达，目前S波段雷达预置的HDA算法参数与WSR-88D相同，C波段雷达中仅有一部分由厂家安装了预置相同参数的算法软件(王瑾等，2011)。

2.1 用于强雹预报的其他环境参数及雷达探测特征

POSH中的统计公式是建立在美国大平原地区外场观测基础上，而我国RPG中的参数并未依据我国的冰雹外场观测结果进行订正，即未修改POSH参数值。由于POSH产品往往高估强雹概率，如仍使用POSH≥50%作为强雹预警阈值，则需利用其他环境参数及雷达探测特征作为进一步判断是否降强雹的辅助阈值。

冰雹形成和增长存在着不同的概念模式，但无论是对超级单体雹暴还是非超级单体雹暴，其共同之处是要有超过0℃层高度的强上升气流，以有利于过冷却水累积区形成(周玲等，2001；许焕斌，2012；蔡淼等，2014)。也就是说，上升气流的强度(达0℃层高度以上)和持续时间决定了冰雹胚胎在过冷却水累积区的停留时间，如果停留时间足够长，雹粒可以增长到足够大而产生地面强雹。

在弱的风垂直切变条件下，对流风暴的组织性一般较差，仅有“脉冲”风暴可产生强雹；在中等到强的风垂直切变条件下，对流风暴常常具有很好的组织性，有可能形成超级单体风暴(俞小鼎等，2006)。根据上升气流强度和冰雹胚胎要在过冷却水累积区停留这两个要求，可以归纳出产生强雹的“脉冲”风暴和超级单体风暴的雷达探测特征(见表 2)。

在POSH≥50%时，表 2中“脉冲”风暴和超级单体风暴共有的雷达特征可用于进一步判断是否降强雹。如，三体散射长钉(Three-Body Scatter Spike，TBSS)是用于确定强雷暴的特征之一，S波段雷达TBSS的存在是雷暴有强雹的直接指示。对强雹探测而言，TBSS是充分而非必要条件(Lemon，1998；郭艳, 2010)。VIL是将雷达反射率因子数值转换成等价液态水量值(Greene et al，1972)，在目前多普勒雷达VIL算法中将反射率＞55 dBz取为55 dBz，即认为反射率＞55 dBz是冰雹而非液态水。一般认为VIL≥45 kg·m^-2会产生1.9 cm以上的冰雹，VIL≥55 kg·m^-2会产生3 cm以上的冰雹(Edwards et al，1998)。VIL密度[即VIL值除回波顶高(Echo Tops, ET)]也可用来预报强雹，通常认为VIL密度＞3.5 g·m^-3会产生强雹(Amburn et al，1997)。风暴顶辐散(即风暴顶正、负速度差值)＞38 m·s^-1, 也有可能产生强雹(Witt et al，1991；吴剑坤等，2009)。

尽管上述任意一种雷达探测特征都可以作为识别单体是否会产生强雹的辅助判据，但TBSS、VIL密度、风暴顶辐散都不是直接的雷达可读取产品。而VIL产品的计算又会受到风暴倾斜及静锥区的影响，会出现高顶高VIL值的风暴不一定产生强雹，而低顶低VIL值的风暴可以产生强雹的不确定性。

2.2 CAPPI产品在强雹预报中的应用

在WSR-88D产品集中并没有CAPPI产品，该产品是北京敏视达雷达公司专门为我国CINRAD WSR-98D所设计的(孟昭林等，2005)。它是将不同仰角的反射率因子值通过双线性插值及加权平均插值到指定高度上的产品。这个产品设计的目的是方便预报员将其与相应等压面场进行比对，如，将CAPPI的高度设成3 km，则可以将其和700 hPa等压面场作粗略比对。CAPPI通常并不列在常规产品集中，将CAPPI作为强雹预报因子使用时，必须指定它的高度和反射率阈值。

POSH降低了对强雹的要求，如40~50 dBz权重为0~1，50 dBz以上权重为1，即认为50 dBz以上即完全为冰雹粒子。这样在强降水为主的事件中，亦会识别出POSH≥50%。

根据冰雹形成的物理过程，强雹粒子增长在接近-20℃层及其以上更冷的区域，故可以考虑将CAPPI的高度设在环境-20℃层高度。通常，55 dBz回波的空间尺度与上升气流强度是有关系的。综合考虑上两个因素，可以使用-20℃层高度上55 dBz范围大于100 km²(根据风暴上升气流的尺度主观设置)作为强雹的辅助阈值。表 3给出了我国8个强对流个例的冰雹相关产品，包括雷达首次识别出POSH≥50%的时间、同时刻CAPPI在-20℃层上的范围及强天气发生的实际时间和类型。

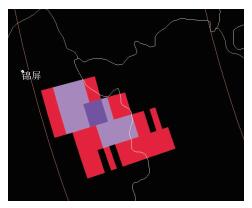
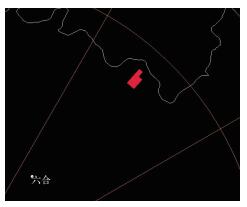
由表 3可见，冰雹指数产品中的最大预期冰雹尺寸(MEHS)远大于实际冰雹最大尺寸。8个个例的POSH都达到50%的预警阈值，使用-20℃层高度上55 dBz＞100 km²的阈值可以将强雹与其他对流性天气进一步区分开。如图 3为2013年3月19日21：45湖南邵阳雷达-20℃层(6.5 km)CAPPI产品，图中利用光标过滤功能显示出≥55 dBz的范围达184.9 km²，地面观测为强雹；图 4为2013年7月7日15：28南京雷达-20℃层(8.5 km)CAPPI产品，≥55 dBz的范围为3.9 km²，未观测到地面降雹。

在具体业务操作中，对S波段雷达，可以将-20℃层高度的CAPPI产品列入PUP(Principle User Position)的常规产品集中。由于将-20℃层CAPPI上55 dBz的面积大小作为强雹预警阈值是基于冰雹形成物理过程及HDA算法思路，因此，对无HDA算法及产品的C波段雷达，可以直接用其为强雹预警提供依据，阈值大小宜根据当地雷达站强对流个例资料统计得到。

3 结论

多普勒雷达探测冰雹的算法发展过程表明，基于反射率预警冰雹有两种方法：(1) 利用雷达观测到的风暴单体反射率特征作预警，如低层钩状回波、弱回波区及回波悬垂等典型超级单体风暴特征；(2) 在SCIT算法识别出的风暴单体基础上，根据雷达探测到的0℃层高度以上的强回波值，用HDA算法直接得到包括POH、POSH及MEHS三种输出的HI产品。

HDA算法是建立在反射率定量化探测基础上，比前期仅依靠反射率特征的冰雹算法提供了更多的冰雹潜势信息。由于冰雹是一种灾害性天气，HDA算法得到的HI产品要能对预报员起提醒作用，因此HDA算法是刻意降低了标准的。在此意义上，即使不考虑算法中所使用参数的地域差异，仍会出现冰雹虚警问题。因此，业务预警中必须参考其他特征作为强雹辅助阈值，如VIL、VIL密度、TBSS等都是有用的指标。用-20℃层高度CAPPI产品上55 dBz的面积大小作阈值，则定量且容易操作。对S波段雷达，可将随季节变动的-20℃层高度CAPPI产品列入常规产品集。对没有HDA算法的C波段雷达，可以直接使用-20℃层CAPPI上55 dBz的面积来预警强雹的发生，阈值宜根据当地雷达站的多个强对流天气个例资料统计确定。

致谢：本文所讨论的问题来源于与中国气象局气象干部培训学院举办的多期多普勒雷达产品与应用培训班学员的交流，在此表示感谢。