引言

沙瓦特指数(以下简称沙氏指数, SI)是Showalter(1953)提出的大气稳定度指数。当SI＜0时，大气为不稳定状态，且负值越大不稳定程度越强。该指数物理意义清晰，与夏季对流性天气的相关性较好，是我国预报员日常业务工作中常用的物理量之一，也经常被用来作为雷暴等对流性天气的预报因子(陈秋萍等, 2010; 曾淑玲等, 2012; 冯民学等, 2012; 何志强等, 2014；王秀明等，2014；周小刚等，2014)。孙继松等(2012)指出，沙氏指数可用来定性判断对流层中层的热力不稳定层结，优点是受日变化影响相对较小，与对流有效位能(CAPE)有较好的正相关，与自由对流高度以上的浮力大小有关。

气象业务中沙氏指数通常采用点绘温度-对数压力图或者利用查算表得到。然而，实际工作中经常需要批量计算包括SI在内的各种对流指数，比如利用数值模式结果计算得到格点上的模式探空数据(陈敏等, 2011)。这时，图解或查表法计算SI的效率就太低了，且图解法结果受人工主观操作影响大，误差不易控制。为此需要设计可靠的数值算法，在实现批量求解的同时保证计算精度，使之与查表法等传统方式得到的结果具有可比性。满足这两个要求的计算方案才真正具有实用价值。

在沙氏指数的数值计算方面，有些学者做了有益的尝试。张年成等(2007)提出了三种方案求解湿绝热方程计算沙氏指数，所给出的5个算例平均绝对误差在1℃以上，这可能与环境因素以及所使用的方程适用范围有关。王学忠等(2009)利用湿绝热过程假相当位温(θ_se)守恒，迭代求解气块温度，并进一步对比查算表研究了其计算方案的适用性和误差分布特点。另外，还有人提出在很小的温压变化范围内θ_se与温度二者近似为线性关系，从而显式计算抬升气块温度和SI(尤伟等, 2011)。从以上现有工作看，王学忠等(2009)计算了整个查算表的完整个例，说服力强，但其精确度(平均绝对误差0.69℃、最大1.36℃)仍有提升空间。在某些接近沙氏指数临界值的对流天气状况下，过大的计算误差还是可能会导致预报不准，因此尽管沙氏指数只是众多对流指数中的一个选择，继续提高其计算准确度仍有积极意义。

本文针对SI计算环节中误差的可能来源，选取多种方案计算分析对比，力图找出更为精确的沙氏指数实用计算方案。

1 基本思想

沙氏指数具体定义为：SI=t_e5-t_p5，其中t_e5为500 hPa的环境温度，t_p5为与气块从850 hPa沿干绝热线上升、到达抬升凝结高度(LCL)后继续沿湿绝热线上升至500 hPa时所具有的温度。可见，气块自850 hPa抬升到500 hPa经历了干绝热和湿绝热两个过程，而湿绝热上升过程中气块温度的求取是计算SI的关键。

本文首先根据干绝热原理计算得到气块到达LCL时的温压状态，然后计算初始θ_se，再利用湿绝热过程中θ_se的守恒性质、通过迭代法求解500 hPa的气块温度。

分析上述过程可推测，SI计算误差的可能来源有三个方面：一是气块到达LCL时温压状态的计算是否准确；二是气块(起始)假相当位温的计算是否准确；三是湿绝热线过程中上升气块的温度求取方法是否可靠。为了尽量减少SI的计算误差，应从这三方面着手。为尽量避免计算过程中的误差传递、放大等效应，要求对各种中间诊断量的计算达到较高的精度。本文在计算LCL处温度(t_LCL)、压强(p_LCL)，以及θ_se等要素时，通过比较从多种方案中择优选用、同时分析各环节误差大小及其对SI计算的影响。

2 计算方案设计 2.1 求抬升凝结高度处的要素

用经验公式和迭代求解两种方案分别计算t_LCL和p_LCL。

方案一：用经验公式计算。求解t_LCL的经验公式很多，本文选取两种常用公式，分别是李洪勣(1985)导出的公式(刘健文等, 2005)

$t_{LCL}^L = {t_0} - \frac{{{t_0} - {t_{d0}}}}{{0.976 - 8.33 \times {{10}^{ - 4}}\frac{{{{(237.3 + {t_{d0}})}^2}}}{{273 + {t_{d0}}}}}} \times 0.976$

(1)

和Bolton(1980) 公式

$T_{LCL}^B = \frac{{2840}}{{3.5{\rm{ln}}T - {\rm{ln}}e - 4.805}} + 55$

(2)

式中, 水汽压e(单位:hPa)的计算可采用Tetens经验公式

${e_s} = 6.11 \times {10^{at/(t + b)}}$

(3)

计算。式中a=7.5, b=237.3，e_s为饱和水汽压(单位：hPa)。如将式(3) 右端t替换为t_d即得水汽压e。上述式(1)~(3) 中，t₀和t_d0表示起始高度的气温和露点(单位：℃)，下标“0”表示起始高度；下标LCL代表抬升凝结高度(下同)；大写T表示绝对温度(单位：K)，即T=t+273.16(下同)。得到T_LCL后，直接利用位温守恒容易得到p_LCL=p₀(T_LCL/T₀)^c_pd/R_d，其中R_d为干空气比气体常数，取为287 J·kg^-1·K^-1，c_pd为干空气定压比热，一般取1004 J·kg^-1·K^-1，故R_d/c_pd≈2/7。

方案二：迭代法求解。利用干绝热过程的位温守恒和比湿(或混合比)守恒这两种守恒性质，可迭代求解LCL处的温度和气压(Stackpole, 1967)。LCL在温度对数压力图上表现为经过初始温压点的干绝热线与经过初始露压点的等饱和比湿线的交点。求解t_LCL和p_LCL的过程其实就是对下列等饱和混合比线(r_s)和等位温线(θ)两个方程在LCL处的联立求解。

${r_s} = 0.622\left( {\frac{{{e_s}}}{{{p_{{\rm{LCL}}}} - {e_s}}}} \right)$

(4)

$\theta = ({t_{{\rm{LCL}}}} + 273.16){(1000/{p_{{\rm{LCL}}}})^{{R_d}/{c_{pd}}}}$

(5)

将式(3) 代入式(4)，并定义D≡(7.5t_LCL)/(237.3+t_LCL)，经简单处理可得

$D = {\rm{lo}}{{\rm{g}}_{10}}\left[ {\frac{{{p_{{\rm{LCL}}}}{r_s}}}{{6.11(0.622 + {r_s})}}} \right]$

(6)

同样将式(5) 整理为

${p_{{\rm{LCL}}}} = 1000{\left[ {\frac{{D\left( {273.3 - 273.16} \right) + 273.16 \times 7.5}}{{\theta \left( {7.5 - D} \right)}}} \right]^{3.5}}$

(7)

迭代步骤：首先给定一个D的初猜值D=D₁, 由于初始位温和饱和混合比为已知, 故利用式(7) 可得到p₁；将p₁代入式(6) 可得D₂；然后再次利用式(7) 得到p₂, 如此迭代直至气压的变化值小于预先给定的小量ε(即|p₁-p₂|＜ε)，满足条件即可由D之定义式得到t_LCL。经验表明, D的初猜值和ε可分别取0.5(约相当于t_LCL为18℃)和0.1 hPa。计算结果表明(算例见2.4节)，该算法效率较高且能达到较高精度。当ε=0.01 hPa时，一般只需迭代4~7次便可完成求解。

2.2 计算假相当位温

假相当位温的含义是，湿空气块在绝热上升(首先干绝热上升到达LCL再湿绝热上升)过程中，在气块本身维持饱和状态下，凝结出来的液态水立即脱离气块不带走系统热量，直到全部水汽凝结脱落完毕以后，所具有的位温(即干绝热下降到1000 hPa时的温度)。可见，假相当位温完全由初始气块的温压湿所决定，具有守恒性。

本文比较了三种方案，分别是下文的Rossby(1932)形式的经典“定义式”，即式(8)；Bolton(1980)推导的式(9)；以及李任承等(1990)提出的一种改进表达式，即式(10)。

对饱和气块，Rossby形式的假相当位温写为

$\theta _{\rm{se}}^R = {\theta _d}{\rm{exp}}\left( {\frac{{L{r_s}}}{{{c_{pd}}T}}} \right)$

(8)

式中，θ_d为湿空气中所含干空气的位温, L为水的汽化潜热，本文采用L=4186.83(597.4-0.57T)计算。对于未饱和空气块，其θ_se等于其干绝热上升达到饱和时的假相当位温，此时上式中气温以及θ_d等诸量均应采用到达LCL时的值。

需要指出，尽管有些书中将式(8) 作为假相当位温的定义式对待，但该式并非θ_se的严格定义，而是Rossby(1932)在当时计算条件很差情况下给出的经典近似式。考虑到该式目前仍有不少研究采用(王学忠等, 2009; 张年成等, 2007; 尤伟等, 2011)，故考察θ_se其他计算方法的效果并与之比较、进而择优选用还是有必要的。下面给出Bolton(1980)、李任承等(1990)提出的表达式，即(9)、(10) 两式。

$\begin{align} & \theta _{\rm{se}}^{B}=T{{\left( \frac{1000}{p} \right)}^{0.2854(1-0.28r)}}\times \\ & \quad \quad {\rm{exp}}\left[ r\left( 1+0.81r \right)(\frac{3376}{{{T}_{\rm{LCL}}}}-2.54) \right] \\ \end{align}$

(9)

$\theta _{\rm{se}}^{L}=\theta _{\rm{se}}^{R}{{\left( 1+\frac{{{R}_{v}}{{T}_{\rm{LCL}}}}{{{L}_{0}}}\rm{ln}N \right)}^{{{r}_{s}}{{c}_{w}}/{{c}_{pd}}}}$

(10)

式(9) 中，绝对温度T，气压p和混合比r为初始高度上的物理量，其中混合比r单位取kg·kg^-1。式(10) 中，水汽比气体常数R_v=461.5 J·kg^-1·K^-1；水的汽化潜热(0℃)L₀取2.5008×10⁶ J·kg^-1；液态水比热c_w=4218 J·kg^-1·K^-1；N的表达式如下：

$N=3+70{{r}_{s}}(1+5{{r}_{s}})$

(11)

式(10) 和(11) 中，r_s为饱和混合比。由式(10) 可见，李任承等(1990)提出的表达式对经典的Rossby形式表达式θ^R_se做了修正，考虑了水物质比热c_w的作用；若忽略之，则退化为式(8)。

2.3 计算抬升气块温度

在计算得到初始高度即850 hPa处的假相当位温θ_se850后，本文利用上升气块的假相当位温在湿绝热过程中的守恒性质，采用迭代方法计算抬升气块到达500 hPa时的温度t_p5, 使气块到达500 hPa时的假相当位温θ_se500与初始θ_se850之差值的绝对值足够小，即A≡|θ_se500-θ_se850|＜ε。主要迭代步骤简述如下(Stackpole, 1967)。

(1) 首先给一个气温初猜值t₁及其增量Δt，并利用t₁计算A，若A＜ε则迭代结束；否则，(2) 令t′=t₁+Δt，利用t′计算A′，若A′＜ε则迭代结束；否则，(3) 比较A与A′的符号，若二者反号，则t_p5即介于t₁与t′之间，令Δt折半，返回第二步；若A与A′同号，则比较二者大小：若A′＜A, 则令t₁和A分别等于前一步的t′和A′，返回第二步；若A′＞A，则将Δt反号并返回第二步。

得到t_p5后，利用SI=t_e5-t_p5即得到沙氏指数。经试验，当ε取0.01℃、气温初猜值t₁及其增量Δt分别取为-2和10℃时，迭代次数不超过6次。

2.4 计算流程以及算例设计

计算500 hPa气块温度及沙氏指数时，流程如下：(1) 首先，用迭代法求得气块从850 hPa沿干绝热线抬升到凝结高度处的温度t_LCL；(2) 分别采用公式(8)、(9) 和(10) 计算初始气块假相当位温，为简便分别称之为RSB、BTN和LRC方案；(3) 利用假相当位温守恒，通过迭代法求三种方案气块达到500 hPa的温度以及SI，并对三种结果作比较分析。

为验证三种方案的效果，仿照王学忠等(2009)的做法，按照寿绍文等(2002, 其附表 7)“500 hPa气块温度查算表”的设计，将850 hPa的气温和露点均按照1℃间隔逐点计算t_LCL、p_LCL、θ_se以及气块温度等物理量。其中，气温的范围由-6~30℃；温度露点差的分布范围是0~36℃，这样的温湿范围几乎涵盖了实际业务中计算SI所能够遇到的所有情形，故说服力较强。计算发现，查算表最右上角的一个计算点的p_LCL＜500 hPa(表明气块抬升到500 hPa为干绝热过程)，这时利用位温守恒性质由LCL处的位温反求500 hPa气块温度。

为便于比较，还计算了前人给出的11个沙氏指数算例(张年成等, 2007; 尤伟等, 2011)。

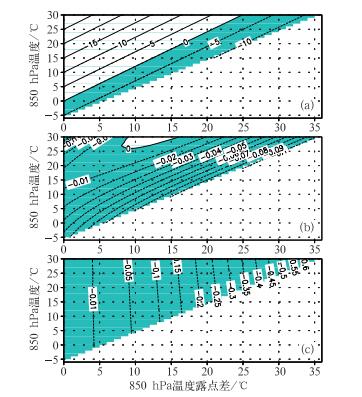
3 结论与讨论 3.1 抬升凝结高度处的要素

由于迭代法计算t_LCL和p_LCL利用了干绝热过程的两个守恒性质，物理意义清楚且迭代精度高，我们认为该算法结果是可靠的。图 1a给出气块自850 hPa抬升至凝结高度时气温的计算结果，以及经验公式与迭代法结果之间的比较。从三者之间的比较来看，Bolton公式与迭代法之间的差别仅在小数点后两位数上，二者差异很小(图 1b)。在极端情况下Bolton公式的计算误差最大也不超过0.1℃。Bolton(1980)认为，式(2) 给出的计算误差约为0.1 K，与图 1结果恰好吻合。李洪勣(1985)公式(式1) 得到的t_LCL之误差与温度关系不大，基本上随湿度的减小而增大，最大可达0.6℃(图 1c)；当t-t_d＜10℃时该式结果比较精确，但当气块较干燥时不推荐使用。

从计算准确的角度，t_LCL的计算可在迭代法或Bolton公式中任选其一。前者物理意义清楚，后者计算简便。抬升凝结高度处气压计算误差的分布态势与温度类似(图略)。

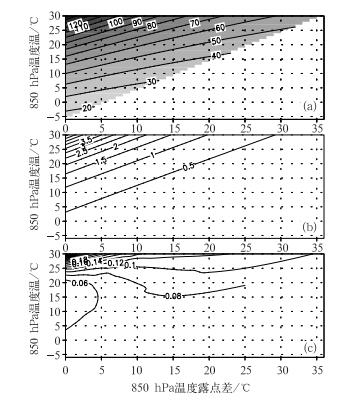
3.2 假相当位温 3.2.1 三种方案计算结果对比

利用上述三种方法计算了850 hPa初始高度假相当位温(图 2)。结果显示，Rossby表达式(RSB方案)得到的结果与另外两种结果差异较大，表现为系统性偏低，偏低的程度随初始气块温度和湿度的增加而快速增大，在较大的温湿范围内误差值在1℃以上(图 2b)。该结果与其他学者的观点至少在定性上是吻合的(Davies-Jones, 2009；李任承等, 1990)。而BTN方案和LRC方案得到的结果虽然在极端高温高湿情况下相差也达到0.37℃ (该情况在现实中很少见)，但在绝大多数情况下二者差别小于0.1℃，可认为结果具有一致性。

分析上述计算结果可推测，Bolton公式和李任承公式的准确度要高于式(8)。首先，从物理过程上讲，Rossby(1932)导出式(8) 时有一个重要的简化，即忽略了水物质比热的贡献。气块抬升到LCL之后继续上升的假绝热过程满足方程(Holton, 1972),

${{c}_{pd}}\frac{{\rm{d}}{{\theta }_{d}}}{{{\theta }_{d}}}+{{c}_{w}}{{r}_{s}}\frac{{\rm{d}}T}{T}+{\rm{d}}\left( \frac{L{{r}_{s}}}{T} \right)=0$

(12)

将式(12) 由抬升凝结高度垂直向上积分到足够的高度，便可由θ_d得到假相当位温。上式由三部分构成，而Rossby公式(式8) 正是忽略掉其中与水物质比热有关的第二项而得到的。Bolton公式与李任承公式用各自的方式考虑了该项的作用。按照假绝热过程的定义，尽管液态水凝结释放的潜热仍留在气块内，但脱落的液态水事实上也是影响系统温度的，忽略掉第二项会低估假相当位温，在特定情况下也会带来可观的误差。其次，Bolton的假相当位温公式是对式(12) 数值积分求解并做拟合得到的，水物质比热的效应隐含在式中；而李任承等(1990)导出式(10) 的方法与之不同，表达式形式也很不一样，但两者计算结果却“殊途同归”，差别很小，两者能够相互印证。第三，利用式(9) 与(10) 计算得到的500 hPa气块温度与查表法之间的误差均明显小于利用式(8) 得到的结果(见3.3节)，这也在一定程度上反证了其精确程度较高。

值得一提的是，Bolton公式(式9) 得到国外一些研究的认可(如Davies-Jones, 2009; Bryan, 2008)，而李任承公式(10) 的应用在文献中还不多见。据本文结果，后者精度可以接受，且在物理意义上优于Bolton公式，值得在相关研究中选用。

3.2.2 抬升凝结高度气温对θ_se计算的影响

为了检验t_LCL对假相当位温计算的影响，我们再次采用Bolton公式计算假相当位温，在计算t_LCL时分别选取2.1节给出的三种方法。三种方法得到的结果之差异在绝大多数情况下仅在小数点后第三位上(图略)。在初始气块高温、干燥的情况下，利用李洪勣(1985)的t_LCL公式得到的θ_se最多比其他两种方案偏高0.02~0.03℃。总体看，三种t_LCL计算方案对假相当位温影响非常小。

3.3 气块温度和沙氏指数

沙氏指数定义为500 hPa环境温度t_e5与气块温度t_p5之差。由于t_e5为观测值，故沙氏指数的计算误差可用t_p5的计算误差来代表(两者大小相等、符号相反)。因此，下面重点讨论气块温度的计算误差。

3.3.1 与查算表的比较

与查算表(寿绍文等, 2002)逐点对应计算500 hPa气块温度，共计703个计算点。首先采用RSB方案，平均绝对误差为0.66℃，最大绝对误差1.33℃(表 1)，无论是平均误差的数值还是分布态势(图略)均与王学忠等(2009)结论大致吻合，这是因为其研究正是采用了式(8) 来计算假相当位温的。当采用BTN方案时，绝均差(误差绝对值的平均值)大幅减小了31.8%，仅为0.45℃；同时最大绝对误差也有明显减小，整体效果令人满意。采用LRC方案计算结果与之类似，计算精度的提升幅度也不错(表 1)。其原因很容易理解：由于假绝热过程中的θ_se处处与起始值保持一致，因此一旦起始值计算不准确，上升到500 hPa时气块温度的计算必然受直接影响，导致沙氏指数计算不准。同时，θ_se的Rossby定义式由于忽略了水物质项，其保守性也逊于另外两种表达式。可见，利用相对精确的假相当位温计算式能大幅改善沙氏指数的计算效果。

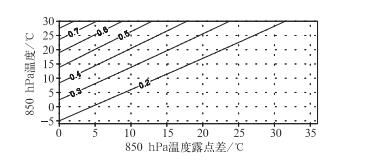
图 3进一步给出本文500 hPa气块温度计算结果(BTN方案)及其与查算表的比较。为突出误差分布的主要特征，图 3b进行了九点平滑。该结果比王学忠等(2009)整体上得到改善，改善的程度可参考图 4。王学忠的结果整体偏低，本文认为其中一个重要原因是其采用了传统Rossby形式的θ_se计算式，如3.2.1节所讨论，该式对θ_se的计算结果偏低；而θ_se偏低导致了计算的气块温度偏低。据图 4，RSB方案500 hPa气块温度偏低一般在0.2~0.8℃。可见，前人计算沙氏指数时，经常将研究的重点放在气块温度的求取方式上，而默认使用Rossby公式计算θ_se；本文使用了更准确的θ_se计算式，其效果是立竿见影的。LRC方案的计算结果与BTN方案很接近，差别仅在小数点后第二位(图略)；RSB方案的计算结果可参考王学忠等(2009)文献的图 1。

本文计算的500 hPa气块温度多数情况下仍然比查表数据偏小(图 3b)。一种解释认为可能是没有考虑气块上升过程中对水滴的卷夹作用所致(王学忠等, 2009)。假绝热过程本身并非严格绝热，气块上升过程中虽将凝结潜热留在气块中，但水滴仍会带走部分热量，也会导致气块温度偏低。计算中用的各种公式误差也是一个原因。比如，利用Bolton公式计算假相当位温最主要的误差来自于将c_pd作为常量的假定，忽略了其随温压的变化，引起的误差最大为0.2℃(Bolton, 1980)。另外，查表值本身的误差也是不可忽视的原因。

3.3.2 与历史个例的比较

张年成等(2007)对沙瓦特指数的计算方法进行了探讨，并通过5个算例比较了其三种算法。后来，王学忠等(2009)、尤伟等(2011)都计算了同样的个例。另外，尤伟等(2011)还选取2008年7月南京地区的6次雷暴日探空数据进行了计算。为直观比较起见，本文也计算了同样的11个个例(表 2和表 3)。

从两个表格结果看：本文LRC和BTN两个方案计算结果接近，精度均高于其他研究，11个算例平均绝对误差仅为0.24℃。特别是表 3给出的个例计算误差仅为0.13℃，计算精度比尤伟等(2011)提高明显。观察图 3b不难发现，表 3的6个个例中，850 hPa温度都在20℃上下且温度露点差很小，刚好位于图 3b误差较小的一段范围内。这似乎也从一定程度说明，本文的计算方案对南京地区夏季雷雨环境下的SI的计算有一定优势。

4 结论

比较了三种假相当位温计算式的精度，并分析了假相当位温对沙氏指数计算的重要影响，提出了计算SI精度较高的实用方案。利用该方案计算了与查算表对应的703个计算点的500 hPa气块温度，与查算表的平均绝对误差为0.45℃; 计算了11个历史个例，沙氏指数的平均绝对误差0.24℃，优于已有文献结果。

(1) 推荐的SI计算方案为：首先利用迭代法或经验公式(2)，求出气块自850 hPa沿干绝热线上升到达LCL时的温度；其次利用Bolton公式(9) 计算气块的初始假相当位温(采用李任承公式10亦可)；然后根据假相当位温的守恒性质，利用Stackpole迭代法计算上升气块到达500 hPa时的温度，进而求出沙氏指数。上述两种迭代过程一般不超过7次即达到较高精度。

(2) 假相当位温的Bolton(1980)公式和李任承等(1990)公式之计算精度明显优于传统的Rossby表达式。后者由于忽略了水物质比热的作用，计算得到的假相当位温系统性偏低，偏低的程度随气块温湿的增加而增大。对850 hPa气块来说，在较大的温湿范围内误差值大于1℃，由此对沙氏指数计算的影响多在0.2~0.8℃。采用更精确的假相当位温计算式能够有效提高沙氏指数的计算精度。

(3) 比较了抬升凝结高度处温压要素的计算方案。建议利用干绝热过程位温和比湿守恒的性质迭代求解，或者用Bolton经验公式直接计算。两种方法计算t_LCL的差别仅在小数点后第二位上，对θ_se的影响多数情况下仅在小数点后第三位，效果略优于李洪勣(1985)公式。

本文提出的方案不但可计算沙氏指数，还可用于计算与湿绝热上升过程中气块温度有关的其他稳定度参数(如CAPE、抬升指数等)，计算精度的提高将会使这些预报指标的计算结果更具通用性，应用前景较好。

致谢：感谢解放军理工大学气象学院王学忠副教授提供查算表数据和部分绘图代码。