引言

多普勒天气雷达能探测到散射体的径向速度，由于其时间分辨率高，对风场研究极有价值。大气是随时间和空间分布的三维运动，理论上讲要有三部雷达同时探测才能准确给出其速度分布特征。由于多普勒雷达网之间有一定的空间间隔，在大部分地区，双多普勒雷达覆盖亦很难达到。因此，从单多普勒雷达径向速度资料获取垂直风廓线场，并在此基础上得到一些热力学、动力学场的分布特性，对短临预报极其重要。由于垂直风廓线(VAD wind profile，VWP)产品不仅有很高的时间分辨率，且垂直方向上的分辨率达300 m，美国预报员曾将其誉为是仅次于垂直累积液态水(vertically integrated liquid，VIL)的最好用产品(Lee等，2000)。随着对多普勒雷达产品和资料的深入了解，我国预报员也从VWP产品上观测到一些可用于业务预报的特征，如：在暴雨发生前VWP产品上“ND”层会遭到破坏(陆大春等，2003；夏文梅等，2008；叶爱芬，2008；陈楠等，2009)；VWP产品上风垂直切变值可作为强对流天气预报指标之一(李德俊等，2011；丁青兰等，2006；赵瑞金，2008；张守保等，2008)；VWP产品上高、低空急流及其向下的脉动与降水强度的增强有着紧密的联系(张京英等，2006)；强降水发生前，VWP产品上水平风向随高度有强烈的顺转(李华宏等，2012；夏文梅等，2008)等，但对这些特征的一些解释仍值得商榷。本文从速度方位显示(velocity-azimuth display，VAD)算法原理出发，对VAD与VWP产品的业务应用误区进行了讨论，并对基于线性风场VAD及扩展的速度方位显示(extended velocity-azimuth display，EVAD)算法的业务应用作了介绍。

1 均匀风场假设VAD算法原理及其产品应用

在一定的假设条件下(如假定风场为均匀或线性分布)，利用多元回归方法对径向速度资料作拟合，则可以由单多普勒雷达得到某特定高度的水平风场特征。最简单的是VAD方法(包括水平均匀风场下的VAD方法和线性风场下的VAD方法)，其他还有EVAD方法，Waldteufel等(1979)提出的VVP(volume velocity processing)方法，Presson等(1987)提出的UW(uniform wind)及陶祖钰(1992)和白洁等(2000)提出的VAP(velolity azimuth processing)方法等。

1.1 均匀风场假设VAD算法原理

假定风场是均匀的、降雨粒子的下落速度也是均匀的，Probert-Jones(1960)最早提出在此种假设下可以反演水平风场，Lhermitte等(1961)详细给出了如何通过特定仰角的方位角扫描来反演水平风场的大小和方向。如图 1所示，将坐标原点设在雷达站点，忽略地球曲率的影响，O_z垂直向上，O_x、O_y分别指向东和北。

在此球坐标中，r是距雷达的距离，α是仰角，β是方位角。假定在雷达周围有大片云雨区，水凝物粒子沿着环境水平风运动，则雷达在某一距离圈(斜距)上(目前的CINRAD WSR-98D Build 10使用的缺省值是30 km)探测到的径向速度可以写为：

$ {V_r} = u\cos \alpha {\rm{sin}}\beta + v\cos \alpha {\rm{cos}}\beta + w\sin \alpha $

(1)

式中, u、v、w为x、y、z方向的速度，垂直速度为环境风垂直速度和水凝物粒子的下落末速度之和。将水平速度大小写为V_h，则式(1) 可写成

$ \begin{array}{*{20}{l}} {{V_r} = {V_h}\sin \left( {{\beta _0} - \pi } \right)\sin \beta {\rm{cos}}\alpha + }\\ {\;\;\;\;\;\;{V_h}\cos \left( {{\beta _0} - \pi } \right)\cos \beta {\rm{cos}}\alpha + w\sin \alpha }\\ {\;\;\; = {V_h}\cos \left( {{\beta _0} - \pi - \beta } \right)\cos \alpha + w\sin \alpha }\\ {\;\;\; = - {V_h}\cos \left( {\beta - {\beta _0}} \right)\cos \alpha + w\sin \alpha } \end{array} $

(2)

此即为均匀风场假设下VAD方法的基本原理。

为与目前CINRAD WSR-98D Build 10中VAD方法拟合的正弦表达式相一致，这里将式(2) 写为

$ {V_r} = {V_h}\sin \left( {\frac{{3\pi }}{2} + \beta - {\beta _0}} \right){\rm{cos}}\alpha + w\sin \alpha $

(3)

当β＝β₀时，有V₁＝－V_hcosα+wsinα，此时V₁为负值，即朝向雷达的最大速度。

当β－β₀＝π时，有V₂＝V_hcosα+wsinα，此时V₂为正值，即离开雷达的最大速度。

故有

$ \begin{array}{l} {V_h} = \frac{{{V_2} - {V_1}}}{{2\cos \alpha }}, \\ w = \frac{{{V_2} + {V_1}}}{{2\sin \alpha }}, \end{array} $

(4)

式中, V₂－V₁为正负速度绝对数值之和；V₂＋V₁为正负速度之和。将式(4) 代入式(3)，则得：

$ {V_r} = \frac{{{V_2} - {V_1}}}{2}\sin \left({\frac{{3\pi }}{2} + \beta - {\beta _0}} \right) + \frac{{{V_2} + {V_1}}}{2} $

(5)

式中, $ \frac{{{V_2} - {V_1}}}{2} $ 为振幅， $ \frac{{{V_2} + {V_1}}}{2} $ 称为对称性。

1.2 VAD及VWP产品 1.2.1 VAD产品

假定在某一高度上风场是均匀的，基本径向速度产品中使用零速度线来推断特定高度(距离圈)上的风速、风向，而VAD算法则是利用式(5) 来确定某个高度上的风速、风向。要获得某一高度上的风向、风速，选取适当的仰角扫描构成的锥面与该等高面相交的曲线(是一个圆)，只要该圆上有至少25个(可调参数)有效径向速度数据点，则通过算法可以得到该高度上的平均风向、风速。VAD产品具体是通过下列步骤获得的：

(1) 给定高度上速度数据的选取

对某一指定高度，选择适当的仰角，使得该仰角与给定高度相交点对应的斜距最接近“VAD距离”(30 km——可调参数)的长度。该仰角下的360°扫描在给定等高面上的轨迹为一圆，该圆上的径向速度数据将用来确定给定高度上的风向风速。

(2) 速度数据点绘

该仰角中给定高度上250 m分辨率的基速度资料点绘在径向速度-方位图上。横轴是方位(雷达的北是0°/360°，南是180°)，纵轴是速度(上部是正的出流速度，下部是负的入流速度)。

(3) 与数据相符合的正弦波(VAD拟合)

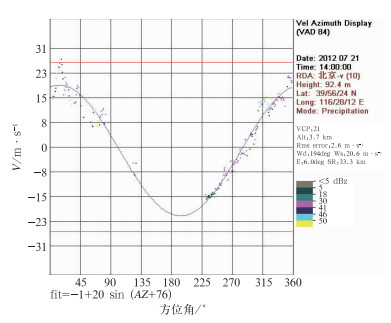
如果图上点绘了超过25个径向速度数据点，则用最小二乘拟合法计算与数据相符合的正弦波。图 2是某指定高度的VAD产品，图底部给出了拟合曲线：FIT＝－1＋20sin(AZ＋76°), 与式(5) 相比较发现，拟合曲线振幅为20，对称性为－1(注：拟合曲线中振幅和对称性都进行了取整运算，实际振幅在VAD产品标注栏显示为20.6 m·s^-1)，并认为拟合曲线的振幅即是估计的水平风速(National Weather Service, Warning Decision Training Branch，1996)。也就是说目前的VAD产品在计算水平风速时，并没有由式(4) 考虑风速与仰角的关系(在我国目前最常用的VCP21模式中，最高仰角为19.5°，由于cos19.5°＝0.94，因此对高层风速所造成的误差在10%以内)。

与式(5)比较，当正弦曲线的位相角为3π/2时，此时是朝向雷达的最大速度，即为风的来向的方位角。因此，对应于图 2，风向为270°－76°＝194°，近似南风。

(4) 对称性和RMS误差

由式(5)，(V₂＋V₁)/2称为对称性，图 2中拟合曲线的第1项即为对称性。在图 2的速度-方位图上表现为零速度线与正弦波曲线中值线之间的差。

RMS误差(均方根误差)是计算每个数据点的径向速度与正弦波上径向速度的偏差(在VAD产品标注栏中有显示)，RMS误差可作为风场估计是否可靠的指标。

目前CINRAD WSR-98D Build 10使用的对称性和RMS误差缺省阈值分别为7和5 m·s^-1(可调参数)，当对称性或RMS误差超过阈值时，VAD产品中仍显示拟合曲线，但认为此时产品是不可靠的。

1.2.2 VWP产品

均匀风场假设下的VAD算法除可得到VAD产品外，还可得到VWP产品。VAD是指定高度上的平均风向风速，而VWP是不同高度上的平均风向风速，它是在VAD产品的基础上得到的。VWP是将不同时刻VAD算法得出的各个高度上水平风用风标表示在同一幅图上而成，水平轴表示体扫时间，最大可选择11个体扫描时间。纵坐标表示高度，最大可包含30个高度。要注意的是，VWP中的高度并不是像VAD产品中的高度一样可以由用户任意指定，在多普勒雷达产品生成(radar product generator，RPG)中的VAD高度选择中有从1000 ft(1 ft＝0.3048 m)(在CINRAD WSR-98D Build 10中已化成以m为单位)到70000 ft(以1000 ft为间隔)共70个高度可供选择，用户可从中任意选择30个高度(National Weather Service, Warning Decision Training Branch，1996)。

当选择30个高度值后，对每个高度选择最接近30 km斜距的仰角(故VWP产品反映的是距雷达站30 km左右的水平风场)，如前所述，该仰角扫描构成的锥面与该等高面相交的曲线是一个圆，由VAD算法，则可以得到30个不同高度的水平风速风向。表 1是北京SA雷达VWP产品部分高度所对应的仰角和斜距(由于地球曲率的影响，不同雷达站相同高度对应仰角上的斜距会有差别)。由表 1可见，指定高度愈高，所用资料的仰角愈高；在低层，仰角的变化很大。

在VWP产品中，下列三种情况之一将显示为“ND”(No Data，无资料)：(1)不足25个资料点；(2)均方根误差大于阈值(缺省值为5 m·s^-1)；(3)对称性大于阈值(缺省值为7 m·s^-1)。

1.3 VAD与VWP产品业务应用讨论

对于VAD与VWP产品的业务应用必须建立在对均匀风场VAD算法的深入了解之上。随着多普勒雷达的布网，我国预报员对VWP产品的业务应用也有了进一步认识。如，可以与常规探空的垂直风廓线一样，通过风随高度顺转或逆转判断雷达站上空冷暖平流层次，从而定性分析大气层结稳定度来判断强对流潜势(王丽荣等，2006；夏文梅等，2008；唐熠等，2005)；可监测冷空气、锋面或槽线的移动情况，即通过VWP产品上同高度、相邻时间风向的交角及风速大小变化来表示各层槽线、切变线、地面锋区过境情况。如槽过境时，同高度风向由南到西南风向北到西北风转变(唐熠等，2005)。下面重点讨论一些对其解释有歧义的业务应用问题。

1.3.1 VWP产品上“ND”的含义

业务人员早就注意到，VWP产品上的“ND”在高度上的变化可以作为强降水产生的前兆特征。认为强降水一般在“ND”基本消失后发生, 并将此解释为大气环境含水量的变化对强天气的影响(陆大春等，2003；夏文梅等，2008)。

尽管业务上可以将此作为局地强降水产生的前兆特征，但其所代表的物理含义则应结合反射率产品和VWP产品的参数设置进行讨论，下面以2012年7月21日北京暴雨为例。

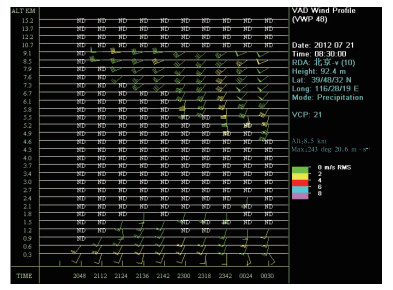
2012年7月21日10时至22日02时，北京经历了自1963年8月8－9日极端降水事件以来最强一次降水过程。导致北京极端暴雨的是中尺度对流系统(MCS)，该MCS系统从形成到消散历经44 h(俞小鼎，2012)。如图 4所示，在7月21日08:30(北京时)VWP产品图上，“ND”层有明显的随时间自上向下的减少过程(注：由于某种原因，资料不是6 min一次连续的)。

从反射率因子图上可知(图略)，07：42的最强单体位于河北满城附近，在北京雷达西北方147.5 km距离圈。由于在中层，距雷达30 km左右，没有探测到反射率因子，因此在VWP产品上中层呈现“ND”。而伴随此单体的层状云区域由于系统的向东北移动，先于主体单体接近雷达，故5.5~10.7 km可以探测到水平风向和风速。随着降水单体主体接近雷达，VWP产品从上至下无“ND”出现，降水开始。

因此，如果将对强降水一般在“ND”基本消失后发生的原因解释为大气环境含水量的变化对强天气的影响，则会将其与判断强对流天气发生的三要素之一“水汽含量”混淆起来。而从VAD算法原理出发，则其明确的物理含义是雷达站上空30 km范围内降水云层厚度的变化，“ND”快速消失说明降水云主体移入雷达站上空30 km范围。同样，当“ND”开始出现并加厚时，说明降水云主体开始移出雷达站上空30 km范围，相应雷达探测范围内降水会逐渐停止。

同时也要注意到，“ND”并不是仅由360°方位角上不足25个数据点造成，均方根误差大于阈值或对称性大于阈值也会使得VWP产品上为“ND”。在VAD产品上，只有第一种情况没有产品显示，在其他两种情况下仍有产品显示。因此，VAD产品除可以用于提供速度退模糊算法所必须的资料外，另一个重要用处就是检查风廓线产品上风资料为“ND”的原因。

故在判断出“ND”是仅由数据点不足引起时，VWP产品上的“ND”可以监测云层的厚度和移入移出雷达站30 km范围的时间。

1.3.2 VAD产品上“对称性”的含义

王丽荣等(2006)认为：VAD产品上正、负速度最大值的差异反映了各个高度层风速的辐合辐散。陆大春等(2003)也指出，降水极值发生前，在多普勒雷达1 km高度VAD产品图上，中位线在“0”速度线以下(即对称性为负)，6 km高度VAD图上，中位线则位于“0”速度线以上(即对称性为正)，说明此时低层辐合，高层辐散，以上升气流为主。即认为对称性表示环境风场的辐合辐散，对称性为负，表示环境风场为辐合，对称性为正，表示环境风场为辐散。

下面从VAD产品的反演算法原理来说明对称性的含义。在均匀风场VAD假定下，认为风场是均匀的，降雨粒子的下落速度也是均匀的。由式(4)，对称性代表的是垂直速度。此垂直速度为环境风垂直速度和云雨粒子的下落末速度之和。如图 2所示，在3.7 km高度的VAD产品图上，对称性为－1(进行了取整运算，可以认为其实际值在－2~－1)，则由式(4) 可以得出垂直速度为负值，即下沉运动。这与前面提到的认为对称性为负值时环境风场为辐合并不相符。

Rogers(1964)在瑞利散射条件下，给出反射率与降雨粒子下落速度的关系为：

$ {w_t} = 3.8{Z^{0.072}} $

(6)

式中, w_t为降雨粒子的下落速度，单位为m·s^-1；Z为反射率，单位为mm⁶·m^-3。如图 2所示，在对应仰角的33.3 km斜距上，反射率在30~45 dBz，由式(6) 算出粒子的下落速度约为6.8~8.0 m·s^-1。因此，在距地面不太高的层次，对称性实际上反映的是粒子的下落速度，并不是环境风的垂直上升速度，也不可以由此用连续方程推断出低、高层的辐散辐合场(连续方程反映的是环境风场之间的关系)。

故VAD产品上“对称性”的含义，在低层是雨滴的降落速度的体现，可以理解为与之相比，环境风场的垂直运动很小。因此，在均匀风场VAD算法条件下，并不能用“对称性”判断环境风场是上升还是下沉运动，是水平辐合还是辐散。

尤为重要的是，VAD产品是在水平均匀风场假设下得到的。水平均匀风场假定本身就已经认为水平辐散辐合为零，故对水平均匀风场假定的产品去讨论辐散辐合问题也是没有意义的。

1.3.3 VWP产品上低层风速突然增加的含义

强降水发生前几个体扫，往往伴有低空急流的突然加强，在VWP产品上会反映为较大的偏南风速由高层向低层的传递过程(张京英等，2006；金巍等，2008)，刘淑媛等(2003)从风廓线雷达上也发现有类似特征。从直观上看，低空急流的加强似乎是由高空动量下传引起的，很多学者也认为这是低空急流形成的原因之一(林毅等，2006；赵娴婷等，2011；屠妮妮等，2007)。但容易引起困惑的问题是，从运动学方程看，动量下传必须有垂直下沉运动，这与通常所认为的强降水发生前环境风场为上升运动是有矛盾的。

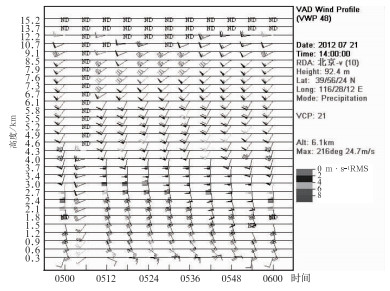
仍以2012年7月21日北京暴雨为例。2012年7月21日09时开始，降水量逐渐增大，在21日14时降水量突然增大(全美兰等，2013)。图 5是2012年7月21日14:00北京暴雨期间的VWP产品，从图上可以清晰地看到强降水发生前有明显的东南风由高层向低层传输的过程。分析VAD产品发现(图略)，13:42VAD产品，低层从0.9到4.0 km，对称性均为负值；4.3 km以上，对称性均为正值。如前面所述，低层对称性反映的是水凝物粒子的下落速度，则一个可能的解释是降雨粒子的下落速度引起高空东南风的动量下传，从而加强了低空东南风急流。

1.4 VAD风廓线资料同化

从业务角度看，由于VAD风廓线资料的间隔时间短(6 min)，可以用三维变分同化方法将其同化到中尺度数值模式中，通过引入风廓线资料来改进水汽输送的影响，从而提高对降水强度和落区的预报准确率。国内外在这方面已有较多尝试。如，马清云等(2001)利用局部VAD方法将径向风反演成水平风同化到MM5模式中，结果表明有助于分析和预报时空尺度较小的中尺度系统。李华宏等(2007)使用GRAPES-Meso模式的三维变分同化系统对雷达风廓线资料进行同化后，风场的初始场明显改善，降水强度和落区预报也有不同程度的改善。总之，在数值预报模式中同化VAD风廓线资料，可以改进风场资料观测的时空不足，有助于改善强对流前期环境预报及降水预报。美国国家环境预报中心、英国气象局等已实现了VAD风廓线在业务预报模式中的应用。但由于变分同化理论对资料有特殊的要求，如何解决VAD风廓线资料业务应用中的质量控制等技术问题仍在不断探索之中(邵爱梅等，2009；朱立娟等，2012a；2012b)。

值得一提的是，目前的VAD风廓线资料依赖于雷达站周围是否存在有效的云与降水粒子，因此在风场资料同化应用方面，不依赖云与降水粒子探测的风廓线雷达可能会有更为广阔的应用空间。

2 基于线性风场假设VAD和EVAD方法的业务应用

由上面的讨论知，均匀风场假设下的VAD方法，不能分离出环境垂直风速与水凝物粒子下落速度的分别贡献，因此也不能得到用于补偿环境垂直运动的水平辐合辐散场。通常，中尺度的辐合辐散及垂直运动场可用于分析强天气发生前环境，因此，利用线性风场假设VAD及EVAD方法由单多普勒雷达得到水平辐散场及垂直运动场，成为短临业务预报中关心的问题。

2.1 线性风场下的VAD方法反演水平辐散及垂直运动场

由式(4) 可见，均匀风场下的VAD方法虽然可以得出垂直速度，但它们是环境风垂直速度和水凝物粒子的下落末速度之和，因此无法由环境风的垂直速度通过连续方程求出水平散度场，这也与其作了水平均匀风场假设是一致的。

考虑局地水平风场为线性变化时的VAD方法由Browning等(1968)首次提出。在水平风场为线性变化时，雷达探测范围内的速度场可以表示为：

$ \begin{array}{l} \bar u = {{\bar u}_0} + \frac{{\partial \bar u}}{{\partial x}}x + \frac{{\partial \bar u}}{{\partial y}}y\\ \bar v = {{\bar v}_0} + \frac{{\partial \bar v}}{{\partial x}}x + \frac{{\partial \bar v}}{{\partial y}}y \end{array} $

(7)

式中下标0表示雷达中心点的值。假定垂直速度是水平均匀的，并用w表示，将式(7) 代入式(1)，且x＝rcosαsinβ，y＝rcosαcosβ，z＝rsinα(图 1)，并写成相应Fourier级数的形式进行比较，则可得水平散度为：

$ \frac{{\partial \bar u}}{{\partial x}} + \frac{{\partial \bar v}}{{\partial y}} = \frac{2}{{r\cos \alpha }}\left({{a_0} - w\sin \alpha } \right) $

(8)

式中a₀为Fourier级数展开的第一项系数(Doviak等，2013)。

Browning等(1968)认为，在斜距为20 km时，计算散度时的系统误差最小。如果假定较低仰角(针对降雪粒子，α＜9°；针对降雨粒子，α＜7°)的粒子下落速度可以忽略不计，则该方法不但可以获得低仰角距雷达20 km半径的辐散辐合值，还可以通过积分连续方程得到相应高度上的环境风垂直速度。

2.2 EVAD方法反演水平辐散及垂直运动场

在Browning等(1968)提出的水平线性风场的VAD方法中，当考虑水凝物粒子下落末速度的非均匀性影响时，式(8) 的计算会有较大误差，尤其是对于较高仰角误差更大。

Srivastava等(1986)首次提出了EVAD方法，通过将式(8) 改写为：

$ \frac{{\partial \bar u}}{{\partial x}} + \frac{{\partial \bar v}}{{\partial y}} = \frac{{2{a_0}}}{{r\cos \alpha }} - 2{w_t}\frac{h}{{{r^2}}} $

(9)

式中，r为斜距，h为与r和仰角α相应的高度，w_t为水凝物粒子下落速度。假定在雷达观测区域内，与水凝物粒子的下落末速度相比，可以忽略环境的垂直速度，则w≈w_t；另外，假定散度项和w_t仅是高度的函数(即水平均匀的)，则在一个浅薄的高度层中，散度项和w_t也可以看成仅是高度的函数，即随高度呈直线分布。因此，可以利用最小二乘拟合法将资料拟合成直线，由拟合直线的截距和斜率可以得到散度和w_t值。

同样，从连续方程出发，由水平散度场可计算出垂直运动廓线。Srivastava等(1986)使用滞弹性连续方程计算表明：较高层的垂直速度可以达到0.15 m·s^-1。但是在利用连续方程，由水平散度场的垂直廓线得到垂直运动时，必须要指定边界条件，而边界条件的假定可能会导致误差，尤其是在云的顶部不能被雷达探测到时。此外，靠近地面的散度廓线有不确定性，因为此时雷达观测资料会受到地面杂波的污染。

线性风场VAD、EVAD方法各有其特点，但在计算水平散度场时都必须去除水凝物粒子下落速度对散度场的影响。另外，从尺度上讲，无论是对于散度还是垂直运动计算，由于雷达探测资料是几分钟一次，单个体扫计算的廓线或许并不能代表中尺度环境场的特点，用时间平均(如每小时平均)后的资料进行计算可能会更好。

3 结论

我国CINRAD WSR-98D Build 10中使用的是水平均匀风场下的VAD方法，由与指定高度对应的仰角上一定斜距上的径向速度资料可以得到VAD产品，在VAD产品基础上则可以得到VWP产品。对于VWP产品上“ND”的含义、VAD产品上“对称性”的含义及VWP产品上低层风速突然增加的含义必须依据水平均匀风场下的VAD算法原理进行解释。

均匀风场下的VAD方法不能得到水平散度值；线性风场下的VAD方法在进一步假定下，可以得到20 km半径的辐散辐合值，还可以通过积分连续方程得到相应高度上的环境风垂直速度。EVAD可以直接计算出降水粒子下落速度和水平风的辐散辐合场。目前，利用线性风场VAD、EVAD方法从多普勒雷达观测的径向速度资料反演风廓线、散度及垂直速度已有一些应用。线性风场VAD及EVAD方法必须在较大范围内有回波限制了它所反演的风廓线和散度的高度。对垂直速度的反演可以用适合中尺度的连续方程，积分水平散度场得到，但要对边界条件作指定。由于雷达探测资料是几分钟一次，单个体扫计算的廓线或许并不能代表中尺度环境场的特点，用时间平均(如每小时平均)后的资料进行计算可能更好。只有在用风廓线雷达直接观测垂直速度时，才可以避免对边界条件的指定，但风廓线雷达的垂直速度特征非常复杂，因为水凝物粒子的信号很难去除，所以它不能代表中尺度运动特征。

目前国内基于线性风场假设VAD和EVAD方法反演水平散度及垂直运动的定量应用并没有正式开展，这方面仍需作大量的相关研究，预期这些定量产品将会在改善数值预报及短临天气预报中发挥较大作用。

致谢：本文讨论的部分问题来源于与中国气象局气象干部培训学院举办的多期多普勒雷达产品与应用培训班学员的交流，在此表示感谢。