引言

霾是大量极细微的尘粒等均匀地浮游在空中，使水平能见度＜10 km的空气普遍混浊现象(中国气象局，2010)。然而，随着社会经济以及城市化进程的不断加快，能源消耗和人类活动导致我国京津冀、长三角、珠三角和成渝等大型城市群的空气中细颗粒物浓度明显增加。空气质量变差不仅对市民的健康构成了威胁，而且由于气溶胶粒子的消光作用会影响能见度，特别是它们吸湿增长后使能见度大幅度下降，从而给交通出行带来很大影响(段玉森等，2005；吴兑等，2011；吴兑，2012)。例如：2013年1月和2014年2月末京津冀地区伴随严重污染的持续性低能见度天气就导致航班大面积延误、高速公路长时间封闭。因此，当今霾已经不是一种纯自然现象，霾的等级预报也已经成为很多气象局的常规业务。

大量研究表明，霾的发生与地面风和相对湿度等气象要素存在密切的关系。当前国内外的霾预报主要有数值预报和模式输出统计预报(model output statistics，MOS)两大类方法。数值预报方法是在大气动力学模式的基础上耦合了化学模块，直接模拟大气污染与大气气象要素场的变化过程(邓涛等，2012；2013；沈劲等，2011)。在业务化过程中，这类方法受到排放清单不确定等因素影响，在日常业务化预报中有较大的局限。MOS方法主要思路是：首先依据污染物浓度数据集筛选出关联性强的气象因子，然后利用统计方法建立预报方程，最后利用模式输出量代入预报方程进行统计预报。陈亦君等(2014)应用基于系统辨识理论的实时迭代模式对WRF模式预报结果进行后处理，建立了上海地区霾天气的模式输出-统计预报系统，结果发现霾日预报成功率达到72.7%~73.7%。程一帆等(2011)在分析能见度与空气污染浓度关系的基础上, 直接利用污染扩散方程建立兰州市冬季霾统计预报模型，在实际预报业务取得较好预报效果。毛宇清等(2011)基于支持向量机(support vector machine, SVM)建立南京地区霾日分类预报模型，结果表明Ts评分均在0.4以上，有霾日14时能见度SVM回归预报结果的准确率在86%以上。郑峰等(2011)利用温州8个气象站点近40年雾日和霾日统计资料，建立包含晴雨、空气污染指数及雾、霾3要素的线性预报系统，发现未来24 h雾、霾预报准确率达57%~66%。上述处理方法均单一地采用了数值天气模式的结果，主要基于霾与气象条件之间的相关性(过宇飞等，2013；刘勇洪等，2014)。如前所述，在污染日益严重的背景下，霾的严重程度受到气溶胶浓度的影响很大。但是，目前尚没有同时采用数值天气预报模式和环境模式的两类输出结果的相关试验研究。

鉴于霾预报的复杂性，本文尝试一种新的思路：即同时选用气象和环境两类不同模式的输出结果(分别为EC模式输出的气象场和BREMPS模式输出的PM_2.5浓度预报场)，再选用恰当的算法对两类数据进行融合，通过建立动态的预报模型实现霾的等级预报。近年来一些数据挖掘算法近年来在气象领域受到关注。KNN算法作为十大数据挖掘的十大经典算法之一，在风(邵明轩等，2006；陈豫英等，2008；涂小萍等，2008)、降水预报(曾晓青等，2008)、云分类(朱彪等, 2012)均有应用。本文尝试将KNN算法应用到北京地区霾等级分类中，以期为建立客观化的霾等级预报系统提供有力的科技支撑。

1 资料和方法 1.1 资料来源

本文所用的常规气象观测资料来源于北京市信息中心，包括温度、气压、湿度、风和能见度等气象要素。环境数据来源于环保部在其官方网站(http://113.108.142.147:20035/emcpublish)公布的PM_2.5小时浓度资料。资料年限为2013年1月1日至12月31日。构建训练样本集时，取北京地区13个区(县)因缺少对应的环保局PM_2.5数据未录入房山区数据集。一天8次、间隔3 h的地面气象资料和PM_2.5数据。

1.2 KNN算法

随着计算机技术的逐渐发展，数据挖掘技术目前在气象中的应用越来越多。黄颖等(2014)将局部线性嵌入算法应用到台风强度集合预报模型，发现能够提高预报效果。刘旸等(2011)利用人工神经网络法反演晴空大气湿度廓线的研究，发现所获得的水汽廓线更加贴近真实廓线。农孟松等(2011)应用主分量分析(PCA)方法，对同一降水预报量的各种数值预报产品进行集成预报研究，发现新的集成预报模型不仅对历史样本的拟合精度好于各个子预报产品，而且对独立样本的实验预报结果也显示出更好的预报准确率及稳定性。KNN是Cover等(1967)提出的一种非参数化监督算法，也是十大经典数据挖掘技术之一，其在统计学领域通常译作“K近邻算法”。KNN是一种通过计算对象间不同特征值距离方法来进行分类的非参数估计技术，也是近年来发展较快的一种实用数据挖掘技术。该算法的优点是精度高、对异常值不敏感、不需要数据输入假定，其缺点是计算复杂度、内存空间开销较大，但随着计算机硬件技术的不断发展，这些缺点变得越来越容易解决。

虽然建立回归预报方程预报法仍然是当前数值天气预报解释应用的一种基本方法，但由于大气运动本身具有混沌性和非线性特征，因此事实上很难用一个或一组简单的线性或非线性回归方程对天气模型精确描述和模拟，故回归预报技术的实际应用效果有时差强人意。KNN算法的核心思想是：客观世界具有规律性和重现性，在相似的条件下往往产生相似的结果，该算法在云分类、风力预报和医疗气象中均有应用。KNN算法在数值天气预报解释应用时，通常直接基于历史天气个例样本建立训练和预测模型，并将天气学预报思路和数值预报结果进行某种融合，故在某些情形下，KNN发挥算法本身的优势，避开建立固定的回归预报方程等不利因素影响。

具体步骤如下：假设有一组历史天气个例样本集合为定义为S。其中，S由i个天气样本组成，而每个天气样本由m个属性变量以及1个标志量构成。其数学表示式为：

$ \mathit{\boldsymbol{S}} = \left\{ \begin{array}{l} \left[ {{X_{11}}, {X_{12}}, {X_{13}}, \cdot \cdot \cdot, {X_{1m}}, {L_1}} \right]\\ \left[ {{X_{21}}, {X_{22}}, {X_{23}}, \cdot \cdot \cdot, {X_{2m}}, {L_2}} \right]\\ \left[ { \cdot \cdot \cdot \; \cdot \cdot \cdot \; \cdot \cdot \cdot \; \cdot \cdot \cdot \; \cdot \cdot \cdot \; \cdot \cdot \cdot \;} \right]\\ \left[ {{X_{i1}}, {X_{i2}}, {X_{i3}}, \cdot \cdot \cdot, {X_{im}}, {L_i}} \right] \end{array} \right\} $

本文的属性变量X_ij分别代表温度、地面气压、相对湿度、露点温度、地面U风、地面V风以及PM_2.5浓度这7个要素，最后一个要素L_i称为标志量(label)，本文中的标志量即为霾等级。利用KNN算法进行霾等级预测可以描述为如下数学模型：假设预报日的温度、气压、相对湿度、露点温度、地面U风、地面V风以及PM_2.5浓度7个要素的集合为Y_i＝{y₁, y₂, …, y_m}，称为预测样本；预测时，首先在训练样本集S集合中找到与预测样本Y_i最相似的K个近邻(K通常为奇数)；然后找出这K个标志量(即霾等级)集合L＝{L₁, L₂, …, L_k}; 最后，按照投票多数原则，选取最多的标志量L_i作为预测样本Y_i预测结果。本文的K近邻居选取采用欧氏距离法进行判定。因此，从本质上说，KNN算法是一种相似算法，KNN算法还被广泛应用于手写码识别(姜文等，2013)和人脸识别(杨淑平等，2013)等领域。本文针对北京的13个气象站点分别构建各自的KNN分类器进行预测。预测时，本文所用的气象要素基于ECMWF细网格模式获得，PM_2.5浓度数据基于BREMPS模式获得。

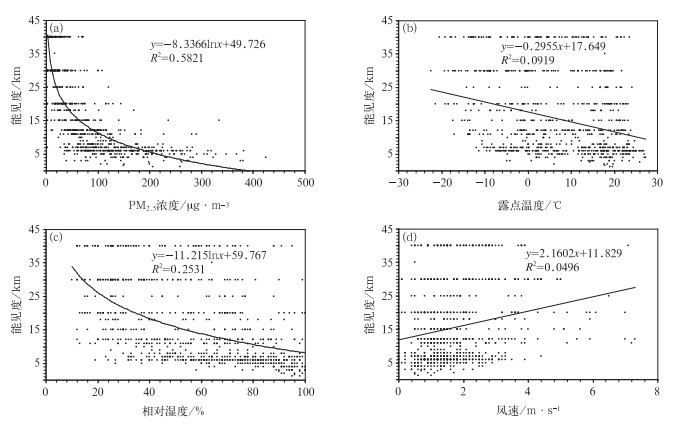
2 试验结果及分析 2.1 KNN分类器中属性变量选取

基于KNN数据挖掘算法进行霾等级预报的关键是构建合理的KNN分类器，而属性变量选取合适与否又对分类器的准确率至关重要的影响。本文的KNN分类器属性变量基于相关分析获得。由霾的定义可知，相对湿度和能见度是定义霾等级的两个关键要素。表 1给出了它们与能见度的相关系数。图 1给出了相关气象要素与能见度的散点图。由图 1a及表 1可知，PM_2.5与能见度的相关系数为0.69，通过了0.001的显著性水平检验。两者可用关系式y＝－8.337lnx＋49.726来进行拟合(式中y为能见度，x为PM_2.5浓度)。由图 1a还可以发现，当PM_2.5浓度＜70 μg·m^-3时，随着浓度增大，能见度急剧变小；反之，当PM_2.5浓度＞70 μg·m^-3时，随着浓度增高，其对能见度的影响程度逐渐减小。由图 1b可知，露点温度与能见度之间呈现负相关关系，其相关系数r＝－0.31，通过0.01的显著性水平检验(表 1)，即随着露点温度升高(水汽含量增加)，能见度逐渐减小。图 1c给出相对湿度和能见度的相关关系。相对湿度与能见度之间也呈现负相关关系，相关系数为－0.49，通过0.001显著性水平检验。能见度和相对湿度之间可用关系式y＝－11.22lnx＋59.767来进行拟合(式中y为能见度，x为相对湿度)，即随着相对湿度增加，能见度逐渐减小。由图 1c进一步可以发现，当相对湿度＜60%时，随着相对湿度的增加，能见度减小的程度较大；反之，当相对湿度＞80%时，随着相对湿度的增加，能见度减小的程度较小。王京丽等(2006)发现空气中的细粒子浓度与大气能见度存在显著的相关关系；曹伟华等(2013)在分析北京的低能见度天气时，也发现相对湿度和PM_2.5浓度是影响能见度大小的两个关键因子。图 1d则反映了风速与能见度之间的相关关系。风速与能见度的相关系数为0.23，两者之间整体呈现正相关关系，即随着风速增大，扩散条件转好，能见度逐渐增大。同时，图 1d也表明当风速＜2 m·s^-1时(即传统意义上的小风速)，能见度一般＜10 km；但是当风速＞2 m·s^-1且＜4 m·s^-1时，既有很大一部分样本的能见度在10 km以上。

上述要素虽然都与能见度有一定的影响，但用单一的气象要素肯定不能很好表征能见度的变化，这也充分说明了能见度变化的复杂性。以风为例，在实际业务值班过程中经常发现，当华北区域整体盛行2~4 m·s^-1的偏北风时(其通常意味着弱冷空气南下，常见于霾天气的结束期)，由于扩散条件转好，北京地区的能见度逐渐转好；而当华北南部地面盛行2~4 m·s^-1的偏南风时，由于其将河北南部的气溶胶例子输送到北京地区，并导致北京地区PM_2.5浓度升高，因此，通常导致本地能见度的下降。但是，当南风风速过大时(5~8 m·s^-1)时，虽然气溶胶输送也很明显，过大的地面风也意味着低层扩散条件转好，能见度反而有所降低。风速、风向对能见度均有较大的影响，这也是KNN训练集中将风分解为u、v风两个分量的原因。

另外，鉴于气温和气压是表征天气统的两个最基本的要素，其对冷空气活动、天气系统的表征具有关键意义，因此也入选了训练属性集。

2.2 K参数的选取

KNN算法中K值的选取对于分类器的准确率有较大的影响。为便于在最邻近的子集中进行投票，K值的选取一般为奇数。若K值太小，则KNN分类结果容易受到噪声的影响；反之，若K的取值过大，则分类器提取的最邻近子集中容易因为包含过多的错误点而对分类准确率产生影响。

交叉验证(Cross validation)俗称循环估计法，其统计学上将数据样本切割成较小子集进行验证的实用方法。通常先在一个子集上做分析，而其他子集则用来做后续对此分析的确认及验证。交叉验证是一种评估统计分析、机器学习算法对独立于训练数据的数据集的泛化能力的实验方法。本文的K值采用交叉验证方式进行确定。表 2给出了K分别取3、5和7时的分类准确率。结果表明(表 2)：当K＝3、5或7时，北京各气象站的交叉检验准确率均在80.0%以上，13个站点的平均准确率分别为88.2%、85.8%和84.7%，且K＝3时，各站的分类准确率明显优于K＝5或7时的结果，而K＝5的结果又优于K＝7的结果。因此，本文采用K＝3来建立KNN模型。

2.3 KNN分类器的准确率分析

为了解KNN分类器对各级霾的预报性能，表 3进一步给出了KNN分类器对各级霾分类的交叉检验结果。表 3中横轴代表霾的预报，横轴表示霾的实况，交叉线(底色为红色的表格)代表预报准确率。由表 3可知：(1) 当KNN分类器预报没有霾时，预报准确率高达91.8%；轻微霾漏报的概率为6.9%，而轻度霾、中度霾和重度霾漏报的概率均＜1%。(2) 当KNN分类器预报有轻微霾时，空报的概率为16.1%，预报正确的概率高达67.4%，轻度霾漏报的概率为11.2%，中度和重度霾漏报的概率均＜5%。(3) 当KNN分类器预报有轻度霾时，空报的概率为4.7%，预报正确的概率高达59.8%。实况较预报偏轻，为轻微霾的概率为21.4%；实况较预报偏重，为中度和重度霾漏报的概率分别为10.4%和3.7%。(4) 当KNN分类器预报有中度霾时，空报的概率仅有1.4%，预报正确的概率为53.4%；实况较预报偏轻，为轻微霾和或轻度霾的概率分别为13.9%和18.8%；实况较预报偏重(实况未重度霾)的概率为12.5%。(5) 当KNN分类器预报有重度霾时，空报的概率为2.6%，等级预报完全正确的概率为60.4%。

综上所述，KNN分类器预报霾的有无时空报或漏报率较低，而且霾的等级预报的准确率较高。但是，当模型预报有霾时，对于相邻等级的区分存在一定的误差。事实上，按照QX/T 113－2010标准进行霾的等级划分时，有些等级范围较窄(例如：规定中度霾能见度为2~3 km)，加上能见度观测本身存在一定的误差，因此本文构建的KNN分类器具有一定的业务实用价值。

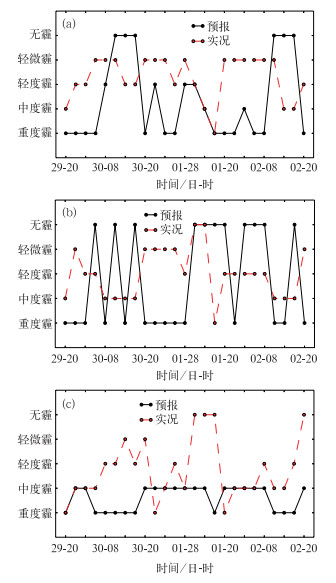
3 基于KNN算法的实际业务预报系统

本研究所用的KNN算法由Python语言进行编码。由于Python语言是一种脚本语言，因此，很便于气象领域搭建实际的业务预报系统。笔者基于KNN算法，搭建了北京地区站点霾等级预报系统。平台的气象要素预报由EC细网格模式输出场通过插值获得，PM_2.5浓度则由BREMPS模式获得。平台每天20时启动一次，起报未来72 h的霾等级，时间分辨率为3 h。2014年8月29日至9月2日，北京地区出现了一次霾天气过程，部分站点伴随降水。图 2给出了北京地区3个基本站(南郊、密云和延庆)72 h时效内间隔3 h的预报与实况的对比。图 2a表明，所有25个观测时次均出现了不同程度的霾，而预报则有19个时次有霾，霾的有无准确率达到76%。但是在8月29日08时的初始阶段，实况没有轻微-中度霾，KNN预报系统预报偏重。8月29日14时和9月2日14时，实况为轻度－中度霾。KNN预报系统预报为无霾，预报偏轻。经过天气分析可知，8月29日14时和9月2日14时EC细网格模式的相对湿度预报较实况偏低，这可能也是KNN模式预报偏轻的主要因素。密云站(图 2b)和延庆站(图 2c)的有无预报准确率分别达到64%和84%，但在霾的等级精确程度略有欠缺。

4 结论

本文研究了将基于数据挖掘技术的KNN算法与天气模式和大气成分模式相结合实现霾的分级客观预报的方法，得到以下结论：

(1) 霾预报的KNN分类器属性特征由温度、气压、相对湿度、露点温度、U风、V风以及PM_2.5浓度等7变量构成，标志项为霾的等级；

(2) KNN分类器分别K取3、5或7的实验结果表明，北京地区13个站点的交叉检验准确率分别为88.2%、85.8%和84.7%，且K＝3时的分类准确率明显优于K＝5或7时的结果。当KNN模型预报的整体预报准确率较高。预报无霾时的准确率高达91.8%，漏报概率很小。KNN模型预报有霾时，空报的概率较低，预报准确率较高；

(3)2014年8月29日至9月2日北京地区一次霾天气过程的预报结果表明，南郊观象台、密云和延庆站的霾有无预报准确率分别达到74%、64%和84%。

应该指出，由于受到大气成分监测资料的限制，本文只采用了2013年的分析数据作为训练样本集，在一定程度上影响了预报准确率。而且，目前KNN霾分类算法直接运用了大气化学模式BREMPS的结果，接下来待PM_2.5浓度资料累积到一定程度后，可对BREMPS的预报结果进行必要的订正。因此，KNN霾分类算法的准确率仍然有进一步提升的空间。