引言

天气系统是时变系统，了解掌握天气系统演变规律需要建立合理的预报模型，并对模型参数进行准确估计。由于天气系统的复杂性，是否能够建立起与天气系统时变特点最优匹配的预报模型成为提高天气预报准确率的关键，这就涉及到对预报模型结构的辨识和模型参数的最优估计问题。随着数值天气预报技术的迅速发展以及数值天气预报模式的不断更新，建立在大量数据基础上的自适应建模技术在数值天气预报产品解释方面得到成功应用，明显提高了天气预报准确率(龙从彬，1992；谢炯光等，2003)。常用的自适应建模技术主要有Kalman滤波(陆如华等，1994；李日华等，2003；白永清等，2013)、多层递阶(孔玉寿，1988；吴钟浚等，1989)、人工神经网络(林健玲等，2006；孙军波等，2010；钱莉等，2010)等。通过不断引入新数据修改原有模型系数，即通过跟踪时变参数动态地把握天气系统变化特征，使模型适应新的数据特性，是这类建模技术的共同特点。然而，研究发现，随着数据的不断增加，引入的新数据对模型系数的修正能力会逐渐降低，即新信息被旧信息逐渐淹没，这种现象通常称之为“数据饱和”(方崇智等，1988)。在方崇智给出的仿真例子中，当数据总量超过200时就会出现“数据饱和”现象，此时参数的估计值趋于不变，系统参数辨识失效。

克服“数据饱和”现象的影响，通常采用降低老数据的作用来实现。常用方法有两种，其一为限定记忆法，其二为遗忘因子法。关于限定记忆法在气象领域的应用已有讨论(赵瑞星等，1999)，而遗忘因子法虽然在水位、洪峰流量等水文参数的预报中得到成功应用(袁晶等，2004；2006)，但在气象要素预报方面的应用还不多见。

最小二乘法因其算法简单、理论成熟、通用性强、精度较高而成为系统参数辨识的最基本最常用方法，在天气预报领域也被广泛应用。因此，本文主要讨论考虑遗忘因子的线性自适应最小二乘建模算法，并利用该方法进行了最高和最低气温预报试验，比较了遗忘因子不同取值对预报结果的影响。实例计算表明，与传统的建模方法相比，该方法对预报模型参数的估计精度较高，因而为提高天气预报准确率提供了一条新思路。

1 遗忘因子线性自适应最小二乘算法

自适应建模技术的核心是不断引入新的数据修改原有预报模型系数，以使其适应新的数据集合，此过程是通过一个被称作系数估计误差阵的方阵P(k)(第k步的系数估计误差方阵)来实现的，通过不断修正该方阵的值来实现修正预报模型的系数。但是系数估计误差阵P(k)是一个随k变化的单调减函数，这一点可从P(k)的表达式看出：

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{P}}\left( k \right) = \mathit{\boldsymbol{P}}\left( {k - 1} \right) - \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( k \right)\left[ {{\boldsymbol{X}}\left( k \right)\mathit{\boldsymbol{P}}\left( {k - 1} \right){\boldsymbol{X}}{{\left( k \right)}^T}} \right.}\\ {\left. {\;\;\;\;\;\;\;\;\;\;\; + {\boldsymbol{I}}} \right]\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{{\left( k \right)}^T}} \end{array} $

(1)

式中，X(k)为因子向量，Γ(k)为通常所称的卡尔曼增益矩阵，P(k)定义为：

$ \mathit{\boldsymbol{P}}\left(k \right) = {\left[ {\sum\limits_{i = 1}^k {\mathit{\boldsymbol{X}}{{\left(i \right)}^T}\mathit{\boldsymbol{X}}\left(i \right)} } \right]^{ - 1}}\ $

按照P(k)的定义，不难看出P(k)是一个正定方阵，因此，式(1) 中的X(k)P(k-1)X(k)^T和[X(k)P(k-1)X(k)^T+I]也是正定方阵。当卡尔曼增益Γ(k)不为零矩阵时Γ(k)[X(k)P(k-1)X(k)^T+I]Γ(k)^T也是正定方阵。因此由式(1) 可以得到P(k)是递减的正定方阵，即当k→∞时，P(k)的元素逐渐趋于零，亦即P(k)将逐渐变成奇异阵。但因P(k)的秩不会随k变化，它始终是满秩的，这就意味着，只能是P(k)逐渐变为一个满秩的零矩阵。由Γ(k)和P(k)的关系知，当P(k)变为零矩阵时，有Γ(k)也变为零矩阵。由于模型系数的修正与Γ(k)有关，当Γ(k)变为零矩阵时，模型系数修正等于零，这时便会产生“数据饱和”现象。所谓“数据饱和”现象是指随着引入的数据越来越多，新数据的作用会变得越来越小，其所提供的信息被淹没在老数据的海洋之中。如果自适应算法对新老数据给予相同的信度，那么随着从新数据中获得的信息量相对下降，对算法的修正能力将会慢慢失去。由于常用的自适应算法一般对新老数据都给予相同的信度，因此，在引入数据较多时，往往就会出现这种“数据饱和”现象。此时模型系数失去了修正能力，即使预报误差较大，也无法更新模型系数进而改进预报效果。特别对于天气变化这种时变过程，这种现象将导致模型参数估计不能及时跟踪系统时变特点，更重要的是，当系数估计误差阵P(k)逐渐变为零矩阵时，由于计算机的舍入误差，可能会使P(k)过早地失去正定性和对称性，造成参数估计远离真值。

考虑遗忘因子是一种克服“数据饱和”现象的方法。考虑遗忘因子的线性自适应建模算法，是在自适应建模算法的基础上通过赋予老数据遗忘因子，降低老数据所提供的信息量，相对增加新数据作用的一种能够克服“数据饱和”现象的线性动态建模方法。

通常情况下，最小二乘准则意义下的动态模型为：

$ {\boldsymbol{U}}\left( k \right) = {\boldsymbol{V}}\left( k \right){\boldsymbol{B}}\left( k \right) + \mathit{\boldsymbol{e}}\left( k \right) $

(2)

式中，V(k)是因子数为m的前k个因子向量X(i), i=1, 2, …, k组成的矩阵，B(k)是前k个模型系数组成的矩阵，U(k)是前k个预报量Z(i), i=1, 2, …, k组成的矩阵或向量，e(k)是前k个随机扰动组成的矩阵或向量。在因子矩阵和预报量矩阵中，加上衰减因子β(0 < β≤1) 后因子矩阵和预报量矩阵记作：

$ \begin{array}{*{20}{l}} {{{\boldsymbol{V}}^*}\left( k \right) = \left[ {{\beta ^{k - 1}}{\boldsymbol{X}}(1),} \right.{\beta ^{k - 1}}{\boldsymbol{X}}(2), \ldots ,}\\ {{{\left. {\;\;\;\;\;\;\;\;\;\;\;\;\beta {\boldsymbol{X}}(k - 1),{\boldsymbol{X}}\left( k \right)} \right]}^T}} \end{array} $

(3)

$ \begin{array}{*{20}{l}} {{{\boldsymbol{U}}^*}\left( k \right)\left[ {{\beta ^{k - 1}}{\boldsymbol{Z}}(1),} \right.{\beta ^{k - 2}}{\boldsymbol{Z}}(2), \ldots ,}\\ {{{\left. {\;\;\;\;\;\;\;\;\;\;\beta {\boldsymbol{Z}}(k - 1),{\boldsymbol{Z}}\left( k \right)} \right]}^T}} \end{array} $

(4)

通常定义：

$ {\boldsymbol{P}}\left( k \right) = {\left[ {{{\boldsymbol{V}}^*}{{\left( k \right)}^{\rm{T}}}{{\boldsymbol{V}}^*}\left( k \right)} \right]^{ - 1}} $

(5)

称之为逆相关阵。如果因子数为m，那么它是一个m×m的方阵。由最小二乘方法很容易得到B(k)的估计：

$ {\boldsymbol{\hat B}}\left( k \right) = {\boldsymbol{P}}\left( k \right){{\boldsymbol{V}}^*}{\left( k \right)^{\rm{T}}}{{\boldsymbol{U}}^*}\left( k \right) $

(6)

由式(3) 和(5) 可以得到：

$ {{\boldsymbol{P}}^{ - 1}}\left( k \right) = \sum\limits_{i = 1}^k {{\mu ^{k - 1}}} {\boldsymbol{X}}{\left( i \right)^{\rm{T}}}{\boldsymbol{X}}\left( i \right) $

(7)

式中，μ=β²，0 < μ≤1，μ称为遗忘因子，其大小可表征“遗忘速度”。当遗忘因子μ=1时，考虑遗忘因子线性自适应建模算法就是普通的线性自适应建模算法。显然由式(7) 可以得到：

$ {{\boldsymbol{P}}^{ - 1}}(k){ = _\mu }{{\boldsymbol{P}}^{ - 1}}(k - 1) + {\boldsymbol{X}}{(k)^{\rm{T}}}{\boldsymbol{X}}(k) $

(8)

由式(4)、(6) 和(8)，有

$ \begin{array}{*{20}{l}} {{\boldsymbol{\hat B}}(k) = {\boldsymbol{P}}(k){{\boldsymbol{V}}^*}{{(k)}^{\rm{T}}}{{\boldsymbol{U}}^*}(k)}\\ {\;\;\;\;\;\;\;\; = {\boldsymbol{\hat B}}(k - 1) + {\boldsymbol{P}}(k){\boldsymbol{V}}{{(k)}^{\rm{T}}}\left[ {\boldsymbol{Z}} \right.(k) - }\\ {\left. {\;\;\;\;\;\;\;\;\;\;\;{\boldsymbol{X}}(k){\boldsymbol{\hat B}}(k - 1)} \right]} \end{array} $

(9)

通常令

$ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}(k) = {\boldsymbol{P}}(k){\boldsymbol{X}}{(k)^{\rm{T}}} $

(10)

因此，式(9) 可以写成：

$ \mathit{\boldsymbol{\hat B}}(\mathit{k}) = \mathit{\boldsymbol{\hat B}}(\mathit{k} - 1) + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}(\mathit{k})\left[ {{\boldsymbol{Z}}(\mathit{k}) - {\boldsymbol{X}}(\mathit{k})\mathit{\boldsymbol{\hat B}}(\mathit{k} - 1)} \right]\ $

(11)

另外，我们可以利用矩阵反演公式将式(5) 改写成：

$ \begin{array}{l} \mathit{\boldsymbol{P}}(k) = {\left[ {\mu {\mathit{\boldsymbol{P}}^{ - 1}}(k - 1) + {\boldsymbol{X}}{{(k)}^{\rm{T}}}{\boldsymbol{X}}(k)} \right]^{ - 1}}\\ = \frac{1}{\mu }\left[ {\mathit{\boldsymbol{I}} - \frac{{\mathit{\boldsymbol{P}}(k - 1){\boldsymbol{X}}{{(k)}^{\rm{T}}}{\boldsymbol{X}}(k)}}{{{\boldsymbol{X}}(k)\mathit{\boldsymbol{P}}(k - 1){\boldsymbol{X}}{{(k)}^{\rm{T}}} + \mu {\boldsymbol{I}}}}} \right]\mathit{\boldsymbol{P}}(k - 1) \end{array} $

(12)

由式(10) 和(12) 可得到：

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}(k) = \mathit{\boldsymbol{P}}(k - 1){\boldsymbol{X}}{{(k)}^{\rm{T}}}\left[ {{\boldsymbol{X}}(k)} \right.\mathit{\boldsymbol{P}}(k - 1) \times }\\ {{{\left. {\;\;\;\;\;\;\;\;\;\;\;{\boldsymbol{X}}{{(k)}^{\rm{T}}} + \mu {\boldsymbol{I}}} \right]}^{ - 1}}} \end{array} $

(13)

这里式(11)~(13) 即为遗忘因子线性自适应最小二乘建模算法公式，其中，P(k)为系数估计误差方阵，是一对称矩阵，Γ(k)为卡尔曼增益矩阵。

一般情况下，模型系数估计初值阵$\mathit{\boldsymbol{\hat B}}(0)$可由有限样本的回归方法或其他方法确定，系数估计误差方阵的初值P(0) 假定是一对角阵或零矩阵。当期望有较快的收敛速度时，P(0) 为相对较大的对角阵。在实际计算时遗忘因子μ必须选择接近于1的正数，通常不小0.95。如果系统是线性系统，且时变特征明显，μ还应选择大些的值，一般应选0.98≤μ < 1(方崇智等，1988)。当μ=1时，上述建模公式就是一般的自适应最小二乘建模算法公式。

2 预报试验

最高、最低气温预报是天气预报的难点，为了研究遗忘因子线性自适应最小二乘算法在天气预报中的应用效果，利用式(11)~(13) 进行了预报试验。预报因子为欧洲数值预报中心发布的山西岢岚气象观测站周围最近四个格点的850 hPa 72 h气温预报值，预报量为岢岚站未来第三天的最高气温和最低气温。试验所用资料为岢岚气象站的实测数据，其中最高气温为1996年6—10月，最低气温为1996年9月至1997年1月。为方便计算，两组数据去掉缺测后统一取样本数为150个。

具体方案如下：

(1) 初值计算：用前20个数据作为初值估计数据，计算自适应最小二乘模型的系数估计初值$\mathit{\boldsymbol{\hat B}}(0)$和系数估计误差方阵的初值P(0)；

(2) 模型系数估计：用前80个数据作为训练数据，对模型系数进行自适应学习训练；

(3) 遗忘因子确定：用第81~130个数据作为预报模型试验数据，进行预报模型训练和检测，择优选择预报模型外参数(遗忘因子)，并用此模型预报最后20个数据；

(4) 独立样本检验：用最后20个数据作为独立样本检验数据，对预报结果进行评价。

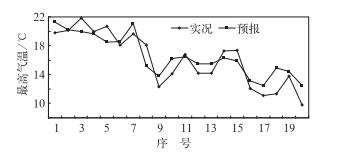
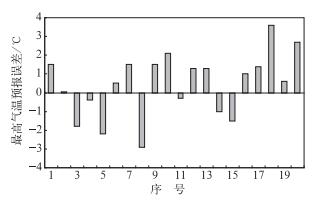
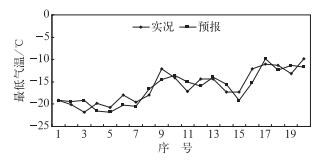
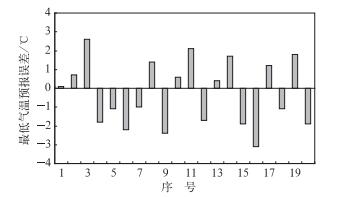
图 1为考虑遗忘因子的最高气温预报结果与实际结果的对比，图 2为最高气温预报误差。图 3为考虑遗忘因子的最低气温预报结果与实际结果的对比，图 4为最低气温预报误差。

计算了μ取值0.91~1.0的预报情况。为了综合评价预报效果，分析不同遗忘因子预报效果差异，除计算了预报平均绝对误差外，还用以下两种预报评分标准对预报结果进行了评价。评价结果见表 1(限于篇幅，只给出了μ取值0.988~1.0的情况)。

评分标准1：采用业务预报评定规范中对气温的评分规定，即预报值在实际值的±1℃范围内得1分，在实际值的±2℃范围内得0.6分，在实际值的±3℃范围内得0.3分，其他不得分。

评分标准2：预报值在实际值的±2.0℃范围内(含±2.0℃)为正确，得1分，否则不正确，得0分。

由表 1可见，取不同的遗忘因子，预报评价结果不同。但不论遗忘因子取值如何，考虑遗忘因子后(μ≠1) 的线性自适应最小二乘建模算法的预报准确率总是不低于未考虑遗忘因子(μ=1) 的预报准确率。特别是当μ=0.989时，考虑遗忘因子后的预报准确率明显优于不考虑遗忘因子的情况。

上述最高气温和最低气温两个预报实例均表明，遗忘因子的选取是影响参数识别结果的一个重要因素，不同遗忘因子的预报结果不同(本文给出的两个预报试验中μ的最优取值为0.989)，但考虑遗忘因子总是有助于提高模型的预报能力。

3 结论

对于目前天气预报中常用的自适应建模算法，当引入数据较多时，可能会产生“数据饱和”现象，此时模型系数失去修正能力，即使预报误差较大，也会因无法更新模型系数而自适应新的数据特性，进而无法改善预报效果。“数据饱和”和计算机舍入误差的共同作用，还很有可能会使系数估计误差阵失去正定性和对称性，造成预报模型参数估计远离真值。为克服这种现象的影响，可采用降低老数据作用的方法来建模。

考虑遗忘因子的自适应最小二乘算法是降低老数据作用、克服“数据饱和”现象影响的方法之一。该方法能够科学利用系统当前及历史数据所含的信息，通过赋予新、旧数据不同的信度，避免新信息被旧信息淹没，使预测模型更有效地自适应于天气系统的时变特征。本文给出了考虑遗忘因子的线性自适应最小二乘建模算法，并用两个实例进行进一步验证，考虑遗忘因子的线性自适应建模算法总是优于传统的线性自适应建模算法(μ=1)，加入遗忘因子不仅可以避免“数据饱和”现象的产生，适当地选择遗忘因子有助于提高预报准确率。

本文的研究是初步的。鉴于天气系统变化的复杂性和多样性，可考虑研究能够根据系统时变特征自动调整遗忘因子的实时辨识算法，如对于慢变化的稳定性天气过程和快变化的转折性天气过程可分别选用不同的遗忘因子，既保证有较快的动态响应速度，又保持有较高的参数辨识精度，通过得到匹配天气过程演变的预报模型参数估计，使模型自适应天气系统动态特性的能力更强，从而达到减小预报误差的目的。