引言

多边形裁剪是计算机图形学和地理信息系统空间分析等领域的重要问题。现有的多边形裁剪算法或者局限于解决某类多边形问题，或者算法结构复杂，时间消耗多，如Sutherl-Hodgeman、梁-Barsky、NLN算法要求被裁剪多边形是凸多边形。也有一些算法能提供通用解决方案，如Weiler-Atherton算法(Weiler et al, 1977, 简称WA算法)、Greiner-Hormann算法(Greiner et al, 1998, 简称GH算法)是公认的可以在合理时间内处理一般多边形(包括凹多边形和带孔洞多边形)的裁剪问题。WA算法和GH算法虽然功能较强，但该算法需要输入的坐标序列具有明确的方向性(顺时针或逆时针输入)。国内有的学者也对多边形裁剪问题进行了研究，但其重点在于改进目前已有算法的运算效率(刘勇奎等, 2003；付迎春等，2006)，其中刘勇奎等(2006)提出的多边形裁剪算法虽然不用考虑输入序列的方向性，但是在实际运算过程中仍要通过技术处理来实现方向的判断，因此并没有从根本上避免方向性问题。

天气预报业务领域亦涉及到多边形的处理。目前日常天气落区预报产品(如定量降水预报和强对流落区预报等)多以多边形顶点坐标方式以MICAPS(Meteorological Information Comprehensive Analysis and Processing System)(李月安等，2010)第14类格式存储，该格式完全不考虑多边形顶点的序列的方向性，因此，在读取该格式的数据或输出成该格式的数据时都无需考虑方向性，这也使得目前已有的多边形裁剪算法无法高效地解决当前的问题。随着气象现代化建设的逐步推进，概率预报和精细化预报在实际业务预报中显得越来越重要。国内学者近年来对强对流天气潜势分析(张小玲等，2012)和分类概率预报(雷蕾等，2012)方面进行了初步探索研究，奠定了较好的基础。国家气象中心强天气预报中心自2011年起开展了分类强对流天气概率预报业务试验，试验的开展要求预报员在同一时间内既要完成强对流落区预报(何立富等，2011)，同时也要完成分类强对流概率预报(毛冬艳，2012)，由于试验开展初期不能在技术上实现两套产品之间的自动转化，因此，增加了预报员的工作量，造成了手工重复劳动。为了减轻预报员的负担，提高工作效率，需要开发“概率预报产品向确定性预报产品的自动转换技术”(Probability forecasts to Deterministic forecasts，简称“P2D技术”)，该技术的核心是多边形合并算法(Polygon Merging Algorithm，简称“PM算法”)。

目前的多边形裁剪算法如WA算法不能够直接用于P2D技术，主要原因有三点：其一，P2D技术的目的是实现多边形的合并(可看作两个或多个多边形取并集)而不是裁剪(可看作两个或多个多边形取交集)，二者虽无本质区别，但侧重点有所不同，其实现方式亦可灵活多变；其二，目前预报产品的坐标在存储时没有方向性(即没有按照顺时针或者逆时针方向存储数据)，无法直接使用WA算法；其三，预报落区为非带孔的多边形，复杂程度有所降低，可以使用相对灵活简单的技术。基于以上需求，需要开发适合气象业务领域的简单准确高效的多边形裁剪技术。由于目前国内气象业务领域尚无合适的满足以上要求的多边形裁剪技术，所以需要开发适合P2D技术的PM算法以满足强对流预报业务需求。本文基于WA算法的基本思路，提出了PM算法，并对其在P2D技术中的应用进行介绍，展望其在相关业务领域的应用前景。

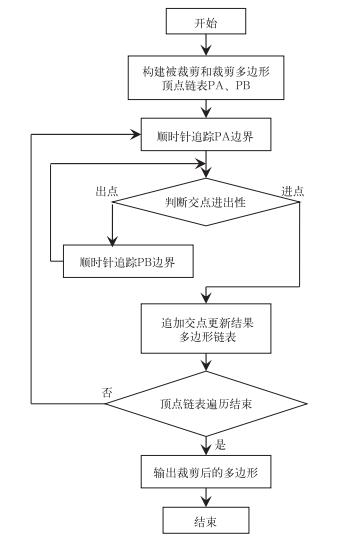
1 技术方法 1.1 WA算法简介

WA算法的基本原理是：由进点开始沿被裁剪多边形追踪，当遇到出点时跳转至裁剪多边形继续追踪，如果再次遇到进点跳转至被裁剪多边形继续追踪。重复以上过程，直到回到起始入点，即完成一个内侧多边形的追踪过程。这里进点和出点分别指被裁剪多边形进入裁剪多边形和离开裁剪多边形的交点(见图 1)。

WA算法技术路线如下：第一，建立主多边形和裁剪多边形的顶点链表；第二，求交点，归类，并按顺序插入到顶点链表中，在两个表的相应顶点间建立双向指针；第三，裁剪，分三步，第一步：如果还有未跟踪过的交点，则任取一个作为起点，建立空的裁剪多边形顶点表，把该交点输入结果顶点表。否则算法结束；第二步：如果该交点为入点，在主多边形顶点表内跟踪，否则在裁剪多边形顶点表内跟踪；第三步：如果跟踪到的是多边形顶点，将其加入结果顶点表，继续跟踪，直到遇到新的交点，重复第二、三步，直到回到起点。

1.2 PM算法

基于引言中阐述的三点理由，本文参考WA算法的思路，设计了适合天气预报业务领域的多边形合并算法(即PM算法)。

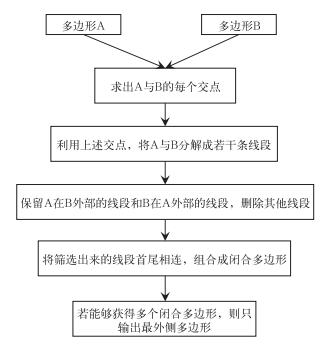
PM算法的基本原理是：根据两个多边形的交点和顶点将这两个多边形分为若干线段，并对每条线段所在位置进行识别，有的线段在另一个多边形里面，有的线段在另一个多边形外面。然后将这些线段首尾相连为若干个闭合多边形，经过处理后，这些多边形必然不会相交，如果有多个多边形，则取最外侧的多边形作为最后的结果输出(图 2)。

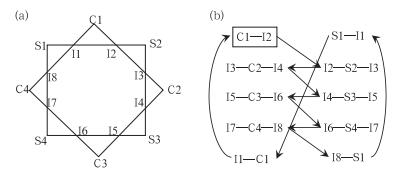
为方便读者将PM算法编制成计算机程序，下面结合图 3对算法的细节进行描述。第一步，设定两个多边形中一个为主多边形(图 3a中的C1—C2—C3—C4)，另一个为副多边形(图 3a中的S1—S2—S3—S4)；第二步，首先从主多边形入手，任选其中一个端点C1作为第一条线的起点进行遍历(即依次对每个节点进行访问)，利用“射线法”判断某个点在一个多边形里面或外面，计算线段C1—C2和副多边形的交点I2和I3，对每条线段进行遍历求交直到该多边形结束，共得到8个交点(I1~I8)，至此，将主多边形分为若干条线段(折线或直线段)，仅保留在副多边形外面的线段(“C1—I2”、“I3—C2—I4”、“I5—C3—I6”、“I7—C4—I8”、“I1—C1”)；第三步，和第二步类似，此时从副多边形入手，将副多边形分为若干条线段，仅保留在主多边形外面的线段(“S1—I1”、“I2—S2—I3”、“I4—S3—I5”、“I6—S4—I7”、“I8—S1”)；第四步，将在第二、三步中获得的所有线段中，选取其中任意一条线段(图 3b中的线段C1—I2) 入手，以其中一个端点C1作为新的多边形的起点，在剩下的线段的所有端点中寻找离第一条线段的另一个端点I2最近的点(这里是I2—S2—I3线段的起点I2)，将这两条线段连接起来组成一条新的线段，按此思路对所有线段进行遍历组合，直到线段闭合(即新的多边形形成)为止(图 3b所示的流程)，如果还有某些线段没有使用，则必然还可以组成另一个新的多边形，重复前面的思路即可，直到所有线段都使用完毕。第五步，如果第四步中获得了一个或多个新的多边形，那么取最外侧的多边形(这里是“C1—I2—S2—I3—C2—I4—S3—I5—C3—I6—S4—I7—C4—I8—S1—I1—C1”)作为最终结果输出，至此，PM算法结束。值得一提的是，按类似的思路，该算法也可用于多边形裁剪。

1.3 PM算法和WA算法的异同点

PM算法和WA算法的思路主要有两点相似。首先，两个算法都需要查找两个多边形的交点；其次，PM算法中将线段归类为在另一个多边形外侧或内侧，与WA算法中将交点归类为入点或出点的思路相似。

这两个算法有以下几点不同：第一，WA算法支持带洞(即非单连通区域)的多边形，这使得该算法需要明确多边形顶点序列的方向(逆时针或顺时针)，而PM算法目前不考虑带洞的多边形，所以不需要考虑多边形顶点序列的方向性；第二，WA算法的目的是要对多边形进行裁剪，所以从“交点”开始遍历查找闭合多边形，而PM算法的目的是要对两个多边形进行合并，所以从一个多边形的“端点”开始遍历查找闭合多边形，二者的出发点不同；第三，WA算法的复杂程度较PM算法高，但运算效率并不是本文研究的重点，所以并没有进行对比测试。可见，PM算法是一种更符合天气预报业务需求的简单准确高效的多边形合并算法。

2 PM算法的业务应用 2.1 在强对流天气预报业务中的应用

目前，国家气象中心强对流落区预报产品主要包括两类，一类是2010年正式业务化的强对流落区预报产品，该产品将预报对象分为三种：雷暴、短时强降水以及雷暴大风和冰雹(在MICAPS中的线条标值见表 1)；另一类是正在进行业务试验的分类强对流概率预报产品，相对于上述业务化产品，该产品一方面进一步细分了强对流天气的类型，即将上述雷暴大风和冰雹的预报细分为雷暴大风预报和冰雹预报两种，且将确定性预报改为概率预报(在MICAPS中的线条标值及概率等级见表 2)。

为了减少预报员不必要的手工重复劳动，需要将雷暴大风概率预报和冰雹概率预报进行自动合并，以实现确定性预报的自动生成。

在P2D技术实现之前，预报员的工作流程是先制作分类强对流概率预报，然后在该产品的基础上再制作一份对应的确定性预报产品，这不仅花费时间，而且一旦修改概率预报落区，必须同时修改对应的确定性预报，因而在每次修改落区的同时要对两套产品进行操作。其实有大量的重复性工作可以通过编制算法来自动完成。基于这种需求，国家气象中心强对流天气预报中心组织开展了P2D技术的研究，而PM算法是该技术的核心。

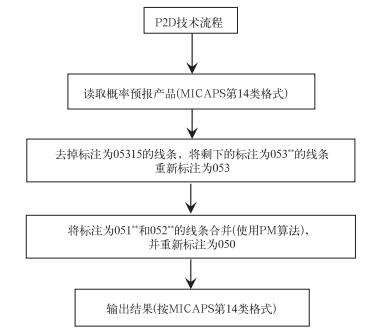
从P2D技术流程来看(图 4)，输入和输出的格式都采用MICAPS第14类格式，在第三步中使用了PM算法。

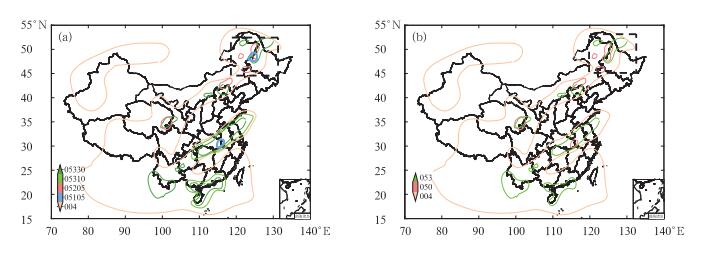
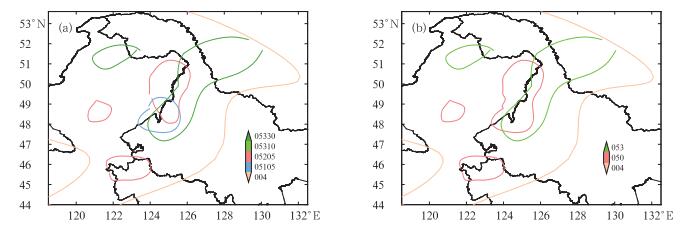
从实际业务中选取了2013年7月7日08时起报的12h时效分类强对流概率预报产品(图 5a)和对应的确定性落区预报产品(图 5b)。图 5b是按照图 2的流程由图 5a自动转换获得。图 6显示的是图 5a和5b中黑色方框(内蒙古东北部和黑龙江西部)放大显示的结果，可见标注为“05205”和“05105”的两条线(图 6a)被合并为一条线，并重新标注为“050”(图 6b)。由图可见，自动转换获得了较好的结果，基本满足业务需求。

2.2 天气预报业务领域应用前景

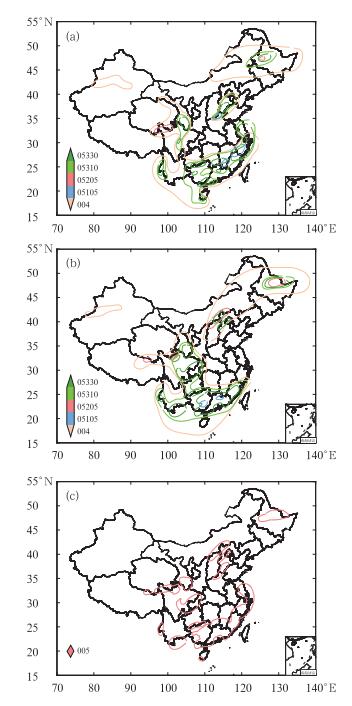
PM算法可在天气预报业务领域进行扩展应用，可将多个时效的定性预报产品合并为更长时效的预报，譬如将20时起报的20时至次日08时的预报(图 7a)和次日08时至次日20时的预报(图 7b)合并为24 h时效的预警产品(图 7c)，具体规范为去掉雷暴落区，将短时强降水、冰雹和雷暴大风的预报落区合并(图 7c中标注为“005”的闭合线所围成的区域)。可提高24 h时效的强对流预警的工作效率。目前国家气象中心发布的某些定性预报产品，如灾害性天气预报中的雾、沙尘预报，环境气象预报中的霾、空气污染气象条件预报及专业气象预报中的森林草原火险预报等都是24 h时效预报，未来如果开展逐12 h或者6 h预报，也可利用PM算法，对多个短时效的预报进行合成生成长时效预报。

诸如此类，比如更长时效的天气过程落区预报生成，也可以应用此算法，因此只要用到多边形合并算法的技术中都可以应用PM算法。

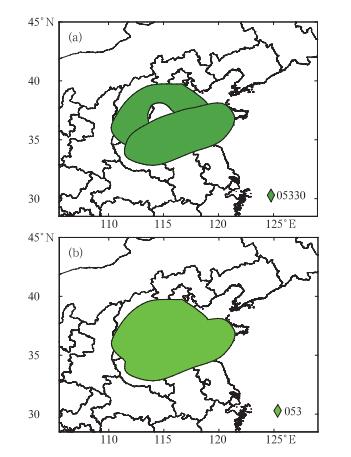
3 讨论

PM算法目前还存在一定的不足之处。当两个或多个多边形合并之后，如果存在内环(即空洞)时(图 8a)，目前的处理方案是忽略这些内环而直接输出最外侧的多边形(图 8b)，不过这种情况不多见，而且对气象领域实际使用的影响很小。未来的工作中，如有需求可对该算法进行改进。

4 结论

本文结合强对流天气预报业务发展的实际需求，提出了PM算法，该算法相对于目前较为流行的WA算法，在气象业务应用方面具有以下优点：PM算法可以完全避免多边形的方向性问题；由于落区预报不会出现带洞的多边形，因此PM算法在设计上更简洁；基于前面两个原因，PM算法实现起来更容易，运行效率更高。目前，该算法已经应用在P2D技术中，并在2013年4—9月进行了业务试运行，结果表明该算法准确、运算速度快且性能稳定，完全能够满足当前业务需求。同时，对该算法的扩展应用前景进行了初步分析，表明该算法在灾害性天气预报，环境气象预报、专业气象预报等天气预报业务领域具有较好的应用前景。一般而言，更长时效的天气过程落区预报生成，或用到多边形合并算法的技术中都可以应用PM算法。