2. 广西区气候中心,南宁 530022;
3. 华东师范大学计算机科学技术系,上海 200241
2. Guangxi Climate Centre, Nanning 530022;
3. Department of Computer Science and Technology, East China Normal University, Shanghai 200241
近10年来,随着多种探测手段的应用与动力模式的不断发展,台风路径机理研究和客观预报水平取得了明显的提高,相比之下,有关台风强度的研究和预报技术的发展明显滞后(陈联寿, 2006;陈建萍等, 2007)。由于严重的强台风往往伴随着强风、暴雨和风暴潮,造成严重的经济损失和人员伤亡,在台风路径预报较正确的条件下,如果对其强度变化估计不足,也同样会造成较大的灾害损失,因此,准确预测台风强度的变化,减轻台风造成的灾害损失是气象防灾减灾的重要研究内容和预报难点。
台风强度的变化受到下垫面、环境气流与台风环流的相互作用及台风本身内部结构变化的综合影响,具有复杂而显著的非线性变化特征,传统的线性预报方法对于提高台风强度的预报并不是太明显,对此国内外进行了许多台风强度预报方法的研究(Goswami et al, 2011;Ritchie et al, 2012;Huang et al, 2013;钱燕珍等, 2013;Yu et al, 2013)。目前气象业务上的台风强度预报,除了综合预报方法外,其他的客观预报方法主要是以统计预报和统计-动力模式为主,并且大多采用逐步回归、最优子集回归、卡尔曼滤波等方法作为预报建模方法,建立预报因子与预报对象之间显著的线性关系。近年来,随着人工智能技术的发展,具有较强处理非线性问题能力的神经网络方法在气象灾害的预报建模应用中获得了较好的成功(刘旸等, 2011;Kwong et al, 2012; 董全等, 2013;曾晓青, 2013)。而粒子群(Particle Swarm Optimization, PSO)算法是广泛采用的一种基于群体智能的全局优化进化算法(Kennedy et al, 1995; 陈莉, 2009; 宋志章等, 2012; 史小露等, 2013)。粒子群算法通过粒子追随自己找到的最优解和整个群的最优解来完成优化,采用简单的速度-位置搜索模型实现整个寻优操作。与遗传算法相比,粒子群算法简单,收敛速度快,易于实现复杂的非线性问题求解。另一方面,流形学习是近年来兴起的专门针对高维数据进行非线性降维的方法,已成为模式识别、机器学习和数据挖掘领域的热点研究问题(张银凤等, 2011;高文曦等, 2012;胡丹等, 2012;白俊卿等, 2013)。流形学习的基本思想是通过揭示高维数据空间的内在几何结构,对其重构后从中提取易于识别的特征,实现非线性降维。其中,局部线性嵌入(Locally Linear Embedding, LLE)降维方法(Roweis et al, 2000)为流形学习的典型代表之一,该算法通过保持数据的局部邻域结构来获取高维数据的低维嵌入,降维后不改变原有流形在局部的相互关系。同时,目前有关神经网络集合预报方法的研究与应用在气象及其他学科领域已取得了一些有效的研究成果(金龙等, 2011;Manzato, 2013;孙照渤等, 2013)。因此,本文以西北太平洋台风强度24和48 h预报作为试验对象,尝试采用局部线性嵌入非线性维数约简与逐步回归计算相结合构造模型输入,并利用粒子群算法客观确定神经网络的网络结构和连接权,通过对预报因子群进行信息挖掘构造出低维的模型输入矩阵,进行粒子群-神经网络的台风强度集合预报模型研究。
1 粒子群-神经网络集合预报模型原理本文尝试通过粒子群算法在期望输出相同的情况下构造众多的神经网络优良个体,由这些个体作集合,并取个体预报值的算术平均值作为集合模型的预报值,进行一种新的非线性人工智能集合预报建模方法研究。
1.1 基本模型在设计采用粒子群算法构建粒子群-神经网络集合预报模型的集合成员个体时,神经网络的基本模型是三层BP网络(Rumelhart et al, 1986)。三层的BP神经网络包含了一个输入层、一个隐层和一个输出层。输入层节点数与输入因子数相同;输出节点只有一个,即台风强度;隐层节点数由粒子群算法确定。隐层的传递函数为logarithmic sigmoid函数,函数形式为f=1/(1+e-x),输出层的传递函数为线性函数,函数形式为f=x。BP网络的主要计算过程可以概括为(Rumelhart et al, 1986):
(1) 设定网络的总体收敛误差ε和最大训练次数T,并随机生成输入层到隐层,隐层到输出层的连接权和阈值。
(2) 输入训练样本,对网络进行有监督的学习训练。采用前馈网络的误差逆传播学习算法,根据网络的实际输出与期望输出之间的误差,调整输入层到隐层,隐层到输出层的连接权。
(3) 反复迭代后,当网络的实际输出与期望输出之间的误差小于ε或达到最大训练次数T时,训练结束。将此时得到的连接权、阈值和预测样本的预报因子输入网络,计算预测值。
1.2 粒子群算法粒子群(PSO)优化算法是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。粒子群算法首先初始化一群随机粒子,每个粒子都代表着优化问题的一个可能解,所有的粒子都有一个由被优化的函数决定的适应值,每个粒子还有一个速度决定它们飞翔的方向和距离。在每次迭代中,各个粒子通过跟踪两个“极值”来更新自己的速度和位置。第一个就是粒子本身所找到的最优解,称为个体极值pbest。另一个极值是整个种群目前找到的最优解,称为全局极值gbest。在解空间中,粒子们追随当前的最优粒子经过迭代搜索找到最优解。粒子群算法具体计算步骤如下(Kennedy et al, 1995):
(1) 初始化粒子群。随机生成N个粒子个体的位置和速度,因此每个个体由两部分组成,第一部分是群体的位置矩阵,第二部分对应粒子的速度矩阵V。群体的位置矩阵包括连接结构矩阵S和权重系数矩阵X;连接结构矩阵S为二进制变量矩阵,对应的连接权存在则该变量为1,否则为0,它控制隐节点数;权重系数矩阵X为浮点数矩阵,取[-1,1]上的均匀分布随机数,它控制网络权值和阈值的大小。
(2) 计算适应度F。计算公式为:
| $F=\frac{1}{E}=\frac{1}{\sqrt{\frac{1}{n}\sum\limits_{j=1}^{n}{{{({{y}_{1}}-{{{\hat{y}}}_{j}})}^{2}}}}}$ | (1) |
其中,E为均方根误差,
(3) 初始化个体极值pbest及全局极值gbest。
(4) 根据粒子适应度,评价每个粒子,更新个体极值pbest及全局极值gbest。
(5) 更新粒子速度矩阵V。粒子速度v的进化方程为:
| $\begin{align} & \upsilon (t+1)=\omega \cdot \upsilon (t)+{{c}_{1}}{{r}_{1}}[pbest(t)-x(t)]+ \\ & {{c}_{2}}{{r}_{2}}[gbest(t)-x(t)] \\ \end{align}$ | (2) |
式中,v是粒子的飞行速度,t是时刻,ω是惯性权重,c1、c2为学习因子,r1、r2为(0, 1) 间的随机数,x是粒子的位置。惯性权重ω采用下式进行自适应调整:
| $\omega (t)={{\omega }_{\max }}-\frac{{{\omega }_{\max }}-{{\omega }_{\min }}}{ite{{r}_{\max }}}\cdot iter$ | (3) |
式中,ωmax、ωmin分别是惯性权重的最大值和最小值;iter、itermax分别是当前迭代次数和最大迭代次数;
(6) 更新粒子位置矩阵中的权重系数矩阵X。粒子的位置x表示权重系数,其进化方程为:
| $x(t+1)=x(t)+\upsilon (t+1)$ | (4) |
(7) 更新位置矩阵中的连接结构矩阵S。连接结构矩阵S的进化方程为:
| $S(t+1)=\left\{ \begin{align} &0,r\ge \frac{1}{1+\exp [-\upsilon (t+1)]} \\ &1,r<\frac{1}{1+\exp [-\upsilon (t+1)]} \\ \end{align} \right.$ | (5) |
式中,r取[0,1]上的均匀分布随机数。
(8) 反复进行(2)~(7) 步的迭代计算,直到当前的迭代次数达到了预先设定的最大次数或满足最小训练误差,则停止迭代,输出最优解。
将最后一代的N个粒子全部解码,得到N个神经网络模型的结构和网络连接权,以其作为BP神经网络的初始连接权和网络结构,再次利用训练样本进入新的BP网络训练,由此得到N个神经网络预报模型。本文采用算术平均法对N个集合成员进行集合预报建模,将每个神经网络个体的预测值作累加再求平均值,作为粒子群-神经网络集合预报模型的预报值。图 1为粒子群-神经网络集合预报建模流程图。

|
图 1 粒子群-神经网络集合预报建模计算流程 Fig. 1 Flowchart for the particle swarm optimization-neural network (PNN) ensemble prediction modeling |
由图 1可以看出,粒子群算法与遗传算法相似,都是从随机解出发,通过迭代寻找最优解,迭代的过程中运用适应度来评价解的品质,但是它比遗传算法规则更简单,没有遗传算法的“交叉”和“变异”操作,而是粒子在解空间追随最优的粒子进行搜索。因此,粒子群算法以其容易实现、精度高、收敛快等优点,在解决复杂的非线性问题中展示了很好的优越性(Kennedy et al, 1995; 陈莉, 2009; 宋志章等, 2012; 史小露等, 2013)。
2 台风强度的人工智能预报试验 2.1 资料在进行西北太平洋台风强度预报试验时,使用的资料取自中国台风网的“CMA-STI热带气旋最佳路径数据集”(http://www.typhoon.gov.cn/),主要包括台风的编号、各时刻台风所在位置的经度、纬度、近中心最低气压和最大风速等要素。以180°以西,0°~45°N的西北太平洋海域的台风为研究对象,盛夏的6—9月是台风最活跃的季节,因此挑选2001—2012年共12年6—9月在此海域内生成或进入这一海域具有48 h以上生命史(气候持续法预报建模需要台风前24 h的样本资料)的台风作为统计个例,台风强度以近中心最大风速表示,并规定台风从进入该海域范围的第一点开始(在此海域生成也一样),每隔6 h观测得到台风强度值为一个预报量样本。由于各月的环境流场特征是不同的,导致不同月内的气候持续因子对未来台风强度变化有不同的影响,以及各月样本个例较多,因而采用分月建立台风强度集合预报模型的方法。为了能对预报建模方法进行比较严格的检验,统一取2001—2011年11年的台风个例为试验的建模样本,2012年的台风个例为独立样本作预报检验。根据台风生命史和研究区域,在24和48 h时效,西北太平洋2001—2012年6—9月各月的台风个数及由各台风6 h强度观测值统计得出的预报量样本数如表 1所示。
|
|
表 1 2001—2012年6—9月西北太平洋台风24和48 h时效的台风个数和台风预报建模样本数、独立预报样本数 Table 1 Number of typhoons over the Northwest Pacific during June-September, 2001-2012 and sample sizes of prediction modeling and independent samples of typhoon intensity prediction experiments at 24 h and 48 h lead time |
在建立台风强度预报模型前,首先根据气候持续法原理(Bessafi et al, 2002),对西北太平洋台风的历史活动规律、初始时刻和前期各种运动特征进行分析,以便科学地选择影响台风未来强度的各种气候学和持续性因子。采用的气候因子主要包括台风所在地区的频数、台风转向位置及其距离等;而台风前期的经、纬度位置及变化,台风前期的风速及变化等作为持续因子,共设计组合得到62个台风强度的气候持续预报因子(限于篇幅,具体因子表略)。
由第1节粒子群-神经网络方法的原理介绍可以看到,粒子群-神经网络方法被应用于预报建模时,其本身并不提供如何去寻找适宜的台风强度预报因子作为网络模型输入,同时在目前的台风强度实际业务预报中,大多是根据气候持续法原理进行预报因子的初选,找到50~60个左右的气候持续因子,再采用逐步回归方法,从中选出8~10个左右的预报因子建立台风强度气候持续法预报模型,而剩余40~50个因子的有用预报信息被完全丢弃,没有进一步利用(Bessafi et al, 2002;Jin et al, 2008)。另一方面,在同样的数学预报建模方法中,模型输入所包含的信息不同对预报模型的预报效果有重要影响。一般而言,模型输入能包含有更多的有效预报信息,则一定能获得更好的预报效果。因此,本文以初选的62个气候持续因子作为建立台风强度预报模型的基本预报因子群,尝试先用逐步回归方法对全部初选预报因子进行筛选后,进一步利用局部线性嵌入(LLE)(Roweis et al, 2000)的非线性特征提取方法,从逐步回归方法筛选后剩余的高维预报因子数据中挖掘出内在的几何结构,以低维表示,再将得到的低维数据集与逐步回归因子共同作为粒子群-神经网络集合预报模型的输入。
LLE算法(Roweis et al, 2000)的主要思想是数据集中的任一数据点都能由其邻域内的所有点线性加权表示,利用样本空间中的局部线性来逼近全局的非线性,同时,由这个数据点映射得到的低维嵌入点同样也可以由原邻域内点的低维嵌入线性加权表示,说明这种线性关系在映射时保持不变。与传统的线性自然正交展开方法(Empirical Orthogonal Functions, EOF)(施能, 2008)相比,EOF在降维过程中保证低维嵌入在高维数据集的方差贡献,但是无法揭示高维数据集的非线性结构和恢复内在的结构,而LLE算法通过局部线性拟合寻找出全局的非线性流形结构,并且在降维过程中,局部邻域结构保持平移、旋转和缩放不变特性,最后将高维数据映射到统一的全局低维坐标系,具有良好的降维效果和较高的识别率(高文曦等, 2012;胡丹等, 2012;白俊卿等, 2013)。
设高维数据集X={x1, …, xn},xi∈RD,降维后的低维坐标Y={y1, …, yN},yi∈Rd,d<D。LLE计算步骤如下(Roweis et al, 2000):
步骤1:寻找每个样本点的k个近邻点。近邻的选取标准一般用欧氏距离。
步骤2:计算重构权值矩阵W。最小化代价函数ε(W):
| $\min \varepsilon (W)={{\sum\limits_{i=1}^{n}{\parallel {{x}_{i}}-\sum\limits_{j=1}^{k}{{{W}_{ij}}{{x}_{j}}}\parallel }}^{2}}$ | (6) |
式中,Wij表示样本点xi同近邻点xj之间的重构权值。满足:① 若xj不是xi的近邻点,则Wij=0;② 否则
步骤3:计算低维嵌入。最小化代价函数Φ(Y):
| $\min \phi (Y)={{\sum\limits_{i=1}^{n}{\parallel {{y}_{i}}-\sum\limits_{j=1}^{k}{{{W}_{ij}}{{y}_{j}}}\parallel }}^{2}}$ | (7) |
式中,yi是xi的低维映射矢量;yj是xi的近邻xj的低维映射矢量;满足
| $\mathit{\boldsymbol{MY}}=\lambda \mathit{\boldsymbol{Y}}$ | (8) |
式中,M=(I-W)T (I-W),是一个N×N的对称稀疏矩阵。要使代价函数式(7) 达到最小值,Y取M的最小d个非零特征值对应的特征向量{ u1, u2, …, u d}为全局低维坐标。
由此可见,LLE算法最后转化为稀疏矩阵的特征值求解问题,不需要迭代算法,避免了局部极值问题。LLE算法具有较少的模型参数和易于理解的图模型构建方法,只需要提前确定2个参数,近邻点个数k和降维后空间的维数d。
2.3 台风强度的人工智能集合预报目前国内外的台风强度预报,通常采用逐步回归方法对气候持续预报因子进行筛选(Bessafi et al, 2002;Jin et al, 2008;施能, 2008)。逐步回归方法是统计预报中较为成熟的预报方案,经过显著性检验挑选出的逐步回归因子,对预报量有显著影响,并且各因子间不存在多重共线性,因此,本文首先运用逐步回归方法选择因子。经过统计发现,6—9月被逐步回归所选入方程的预报因子并不尽相同,而台风前期的位置及其速率等气候持续因子是最容易被选入方程的。经过逐步回归方法筛选后的众多剩余因子中,必定存在着大量对于预报量还有很大贡献的预报信息。为了充分挖掘利用全部气候持续因子的有用预报信息,建立更合理的模型输入学习矩阵,同时考虑到预报因子与台风强度之间的非线性关系,因而采用LLE方法对这部分没被逐步回归方法入选的因子进行非线性特征提取。LLE方法能够实现高维数据映射到一个全局低维坐标系,同时保留近邻点之间的关系,使得固有的几何结构能够得到保留。该方法不仅能够有效地发现数据的非线性结构,同时还具有平移、旋转和缩放不变特性。
以6月台风强度24 h预报量及初选得到的62个气候持续预报因子为例(见表 1和表 2),具体作法为:首先以F=3,采用逐步回归方法从62个因子中筛选出7个预报因子,再对剩余的55个因子,利用LLE方法作非线性特征提取,取近邻个数k=15,数据空间降至2维,将这2个非线性的LLE因子与前面7个逐步回归因子,共9个预报因子作为模型输入,建立6月24 h台风强度的基于LLE的粒子群-神经网络集合预报模型。在粒子群算法的进化计算过程中,进化代数为50,粒子数为30,c1=c2=2,惯性权重最小值和惯性权重最大值分别为0.4和0.9,输入节点为模型输入的因子个数,输出节点为1,隐节点的搜索空间为输入节点的0.5~1.5倍。神经网络训练次数为200次,学习因子为0.9,动量因子为0.7,总体收敛误差为0.01。进化计算结束后,对粒子群的30个个体解码,得到30个神经网络预报个体,其中隐节点数为5~8。将所有神经网络预报个体作合成,建立最终的西北太平洋台风强度集合预报模型。表 2列出了各月各时次的西北太平洋台风强度预报在首次建模时,采用上述方法得到的粒子群-神经网络集合预报模型的输入维数。
|
|
表 2 首次建模的台风强度各月各时次预报因子计算结果统计 Table 2 Number of predictors for the first typhoon intensity prediction modeling in each month at each lead time |
为了保证独立样本的预报与实际预报一致,预报试验采取逐次的方式。例如,对6月台风强度24 h预报时,建模样本数为445(表 1),利用预报模型对第一个独立样本作预报,然后再以445个建模样本加上前面第一个独立样本(这时,第一个独立样本的实况已知),以446个样本作为建模样本,对第二个独立样本进行预报,以此类推,一直到用487个样本建模预报第43个独立样本。所有的逐次预报中,粒子群-神经网络模型和LLE算法的所有参数保持不变,并且每次预报都是对初始的62个因子重新计算逐步回归因子以及重新进行LLE降维。对其余各月各时次的台风强度预报,也采用与6月24 h数据完全相同的预报方法,运用基于LLE的粒子群-神经网络模型对独立样本进行逐次预报试验。经统计得到,24 h各月(6—9月)独立样本预报的预报平均绝对误差依次为4.04、4.51、4.94和5.10 m·s-1,4个月的预报平均绝对误差为4.76 m·s-1;48 h各月(6—9月)独立样本预报的预报平均绝对误差依次为4.95、6.22、7.79和5.52 m·s-1,4个月的预报平均绝对误差为6.53 m·s-1(见表 3)。逐次预报过程中,所有参数都是固定的,并且每增加一个建模样本,重新计算预报模型输入,这使得独立样本的预报具有很好的客观性。图 2为基于LLE的粒子群-神经网络集合预报模型(PNN-LLE)对6—9月台风强度24和48 h时效独立样本的预报值与台风强度的实况值对比图。
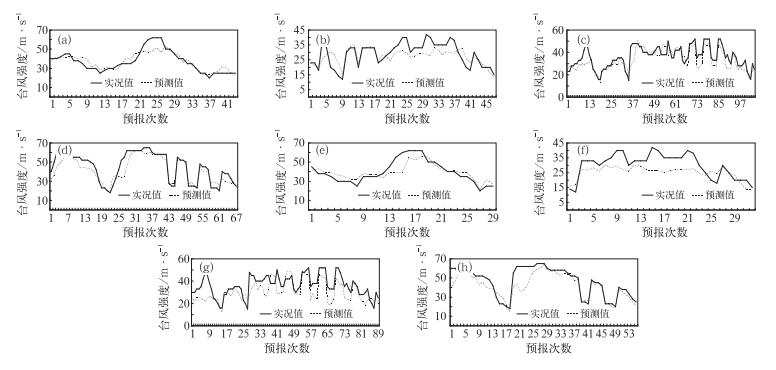
|
图 2 基于LLE的粒子群-神经网络集合预报模型对6—9月台风强度24 (a, b, c, d)和48 h(e, f, g, h)时效独立样本的预报值(虚线)和台风强度的实况值(实线) Fig. 2 Predicted (dashed) values of the typhoon intensity of independent samples in June-September at 24 h and 48 h lead time by the PNN-LLE ensemble model and the corresponding observed (solid) values |
|
|
表 3 集合预报模型(PNN-LLE)与气候持续法预报模型(CLIPER)对台风强度独立预报样本的误差统计及比较 Table 3 Statistics of the prediction errors of the PNN-LLE ensemble model and the CLIPER prediction model |
气候持续法(CLIPER)是国内外运用较为广泛的台风路径、强度客观预报方法,它是以台风前期的位置和强度变化等作为主要的预报因子(Bessafi et al, 2002;Aberson et al, 2003)。一般认为CLIPER方法是评估预报模式技巧的标准(Jin et al, 2008;Lu et al, 2010;Chand et al, 2011;钱燕珍等, 2013),如果本文构建的这种新的人工智能集合预报方法比CLIPER法有更好的预报精度,可以为台风强度客观预报提供新的预报工具。
目前,采用以台风气候持续因子建立的台风客观预报方法,大多是采用回归分析方法建立预报方程(Bessafi et al, 2002;Aberson et al, 2003;施能, 2008)。面对初选得到的众多预报因子,选取不同的F值,会有不同的预报因子组合得到相应不同的预报方程,这些不同的预报方程的预报能力是有差异的。为保证对比的合理性,直接利用表 2中各月各时次数据在F=3情况下,经逐步回归方法筛选得到的气候持续预报因子作为模型输入,以相同的预报建模样本和独立预报样本,分别建立2001—2012年6—9月西北太平洋台风强度24和48 h的气候持续法预报方程,采用逐次预报方式,将各月各时次台风强度预报方程分别对独立样本进行预报检验。表 3为各时次6—9月台风强度独立样本的气候持续预报模型的预报误差情况。6—9月独立样本在2个时次的预报平均绝对误差分别为6.19 m·s-1(24 h)和8.77 m·s-1(48 h),误差明显大于基于LLE的粒子群-神经网络集合模型的独立样本预报结果4.76 m·s-1(24 h)和6.53 m·s-1(48 h);预报均方根误差分别为8.04 m·s-1(24 h)和10.80 m·s-1(48 h),误差也大于基于LLE的粒子群-神经网络模型的独立样本预报结果6.26 m·s-1(24 h)和8.47 m·s-1(48 h)。进一步对各月各时次台风强度独立样本的预报误差作统计发现,虽然两种预报模型的预报建模样本、独立样本和初选预报因子完全相同,但是基于LLE的粒子群-神经网络台风强度集合预报模型比气候持续法台风强度预报模型有了较明显的提高,预报技巧水平分别为23.10%(24 h)和25.54%(48 h)。模型B相对于模型A的预报技巧水平的计算公式为:
| $\text{预报技巧水平=(模型A预报误差-模型B预报误差)/模型A预报误差 }\!\!\times\!\!\text{ 100 }\text{% }$ | (9) |
式中,模型A、B分别表示气候持续法和本文所应用的新方案基于LLE的粒子群-神经网络集合预报模型。
2.5 与变动LLE方法近邻个数进行预报试验的对比分析为了进一步检验基于LLE的粒子群-神经网络集合模型的预报性能是否稳定,对LLE算法的近邻个数分别取20、30和35,数据仍然降至2维,其余粒子群-神经网络参数保持不变,采用相同的样本及预报建模方法,建立基于LLE的粒子群-神经网络集合预报模型,对2001—2012年6—9月台风强度24和48 h的独立样本作预报检验,预报结果见表 4。当k=20时,6—9月独立样本在2个时次的预报平均绝对误差分别为4.82 m·s-1(24 h)和6.37 m·s-1(48 h),预报均方根误差分别为6.28 m·s-1(24 h)和8.23 m·s-1(48 h);当k=30时,预报平均绝对误差分别为4.63 m·s-1(24 h)和6.32 m·s-1(48 h),预报均方根误差分别为6.17 m·s-1(24 h)和8.15 m·s-1(48 h);当k=35时,预报平均绝对误差分别为4.79 m·s-1(24 h)和6.28 m·s-1(48 h),预报均方根误差分别为6.34 m·s-1(24 h)和8.12 m·s-1(48 h)。可以看出,随着近邻个数的变动,误差情况虽有所差别,但是3种情况下,基于LLE的粒子群-神经网络集合模型的预报误差均小于气候持续法的预报结果。
由表 3和表 4的误差统计结果表明,经与同样预报对象的传统方法的多指标对比分析,在变动近邻个数的情况下,基于LLE的粒子群-神经网络集合模型预报结果相差不大,预报结果稳定可靠。当邻近个数为15、20、30和35时,基于LLE的粒子群-神经网络模型相对于同时次同月份气候持续法的预报技巧水平均为正技巧。当k=20时,基于LLE的粒子群-神经网络集合方法相对于各时次气候持续法的预报技巧水平分别为22.13%(24 h)和27.37%(48 h);当k=30时,预报技巧水平分别为25.20%(24 h)和27.94%(48 h);当k=35时,预报技巧水平分别为22.62%(24 h)和28.39%(48 h)。总体上,技术水平提高22%以上,最高达到28%。这主要是因为气候持续法预报方程是采用线性回归分析方法建立的预报方程,而台风在移动过程中其强度、内力及外部环境场都会发生非线性的变化,粒子群-神经网络方法是一种人工智能的非线性预报建模方法,具有非线性映射和很强的自适应学习能力,可以更好地反映台风强度的非线性变化特点,进一步采用LLE方法进行因子的非线性特征选取,给模型的因子矩阵添加了更为丰富的预报信息,因此独立样本的预报平均绝对误差和预报均方根误差明显下降。并且对于LLE算法,本文取k=15、20、30和35分别进行预报试验,均获得了较好的预报效果。这表明,近邻个数k在一个合适的范围内取值,其预报效果是比较稳定的,这有利于该方法在实际预报中的应用。
|
|
表 4 基于LLE的粒子群-神经网络集合模型对不同近邻个数的台风强度独立样本预报误差(单位:m·s-1)及与气候持续法相比预报技巧水平(单位:%) Table 4 Statistics of the prediction errors of the PNN-LLE model (unit: m·s-1) and the forecast skill as compared to the CLIPER method (unit: %) |
台风是一种预报难度很大的重要灾害性天气,本文以西北太平洋海域的台风样本和相关气候持续预报因子为基础,针对台风强度的非线性变化特征,采用粒子群算法,神经网络和局部线性嵌入系统降维三种非线性人工智能技术方法,研究建立24和48 h时效的台风强度预报模型,是一种新的尝试。一方面,局部线性嵌入通过保持数据的局部邻域结构来获取高维数据的低维嵌入,很好地揭示了高维数据的非线性结构。另一方面,将粒子群算法和神经网络相结合,利用粒子群算法的全局随机搜索能力,对神经网络的权值和阈值等主要参数进行优化,以比较客观的方法确定神经网络结构。在相同的条件下,独立样本的预报结果表明,基于LLE的粒子群-神经网络集合预报模型的试验结果明显好于只考虑气候持续预报因子的气候持续法的预报结果,各月各时次预报技巧水平相对于气候持续法均为正的技巧。主要是因为新方案中所运用的逐步回归方法能够将经过显著性检验的一些因子自动提取出来,再采用LLE方法对剩下的因子进行非线性特征提取加入模型输入矩阵,充分挖掘了全部预报因子群的有效预报信息,因而预报效果较好。另外,在变动LLE算法参数的情况下,基于LLE的粒子群-神经网络集合预报模型的预报结果也较为稳定。与台风路径预报方法研究工作相比,目前有关台风强度的客观预报方法研究工作相对较少,本文提出的这种新的非线性智能计算预报模型与其他一些台风强度的客观预报方法研究工作相比,虽然所研究预报的台风个例有所不同,但总体而言,本文的方法显示了较好的预报能力,可以为台风强度客观预报应用提供一种新的思路和方法。
虽然本文提出的基于LLE的粒子群-神经网络台风强度集合预报模型与线性的气候持续法预报试验相比,预报效果提高比较明显,但是,深入分析可以看到,这种新模型对台风强度极值的预报与台风强度实况有一定的差距,这还需要作进一步的深入研究和改进。另外,LLE方法作为一种新的非线性气象数据处理技术,目前在气象学科中的应用研究相对还比较少,这提示我们该方法可以进一步在其他气象要素的预报建模研究中进行深入的应用研究。
白俊卿, 闫桂荣, 王成, 2013. 利用局部线性嵌入的模态识别[J]. 西安交通大学学报, 47(1): 85-89. |
陈建萍, 周传灿, 尹洁, 2007. 国内外热带气旋强度变化研究现状[J]. 气象与减灾研究, 30(3): 40-47. |
陈莉, 2009. 基于粒子群神经网络优化的相关证据合成及应用[J]. 系统仿真学报, 21(3): 711-715. |
陈联寿, 2006. 热带气旋研究和业务预报技术的发展[J]. 应用气象学报, 17(6): 672-681. DOI:10.11898/1001-7313.20060605 |
董全, 黄小玉, 宗志平, 2013. 人工神经网络法和线性回归法对降水相态的预报效果对比[J]. 气象, 39(3): 324-332. DOI:10.7519/j.issn.1000-0526.2013.03.006 |
高文曦, 于凤芹, 2012. 基于局部线性嵌入算法的汉语数字语音识别[J]. 计算机工程与应用, 48(31): 105-107. DOI:10.3778/j.issn.1002-8331.2012.31.023 |
胡丹, 薛源, 2012. 基于改进有监督局部线性嵌入的地震属性降维优化[J]. 国土资源科技管理, 29(6): 120-124. |
金龙, 黄颖, 何如, 2011. 卫星云图的遗传神经网络集合预测模型研究[J]. 计算机工程与应用, 47(32): 231-235. DOI:10.3778/j.issn.1002-8331.2011.32.067 |
刘旸, 官莉, 2011. 人工神经网络法反演晴空大气湿度廓线的研究[J]. 气象, 37(3): 318-324. DOI:10.7519/j.issn.1000-0526.2011.03.009 |
钱燕珍, 张程明, 孙军波, 等, 2013. 用数值预报释用方法做近海及登陆热带气旋强度预报[J]. 气象, 39(6): 710-718. DOI:10.7519/j.issn.1000-0526.2013.06.007 |
施能, 2008. 气象科研与预报中的多元分析方法[M]. 北京: 气象出版社, 72-114.
|
史小露, 孙辉, 李俊, 等, 2013. 具有快速收敛和自适应逃逸功能的粒子群优化算法[J]. 计算机应用, 33(5): 1308-1312. |
宋志章, 马丽, 李奇楠, 等, 2012. 基于粒子群神经网络的发动机故障诊断方法[J]. 计算机仿真, 29(4): 272-275. |
孙照渤, 谭桂容, 赵振国, 等, 2013. 中国东部夏季雨型的人工神经网络集合预测[J]. 大气科学学报, 36(1): 1-6. |
张银凤, 王晅, 马建峰, 2011. 基于最优邻域图的等距映射流形学习算法[J]. 计算机工程与应用, 47(14): 124-127. DOI:10.3778/j.issn.1002-8331.2011.14.035 |
曾晓青, 2013. BP神经网络在建模中的参数优化问题研究[J]. 气象, 39(3): 333-339. DOI:10.3969/2012jms.0122 |
Aberson S D, Sampson C R, 2003. On the predictability of tropical cyclone tracks in the Northwest Pacific Basin[J]. Mon Wea Rev, 131(7): 1491-1497. DOI:10.1175/1520-0493(2003)131<1491:OTPOTC>2.0.CO;2 |
Bessafi M, Lasserre-Bigorry A, Neumann C J, et al, 2002. Statistical prediction of tropical cyclone motion: An Analog-CLIPER approach[J]. Wea Forecasting, 17(4): 821-831. DOI:10.1175/1520-0434(2002)017<0821:SPOTCM>2.0.CO;2 |
Chand S S, Walsh K J E, 2011. Forecasting tropical cyclone formation in the Fiji region: A probit regression approach using Bayesian fitting[J]. Wea Forecasting, 26(2): 150-165. DOI:10.1175/2010WAF2222452.1 |
Goswami P, Mallick S, Gouda K C, 2011. Objective debiasing for improved forecasting of tropical cyclone intensity with a global circulation model[J]. Mon Wea Rev, 139(8): 2471-2487. DOI:10.1175/2011MWR3600.1 |
Huang Ying, Jin Long, 2013. A prediction scheme with genetic neural network and Isomap algorithm for tropical cyclone intensity change over Western North Pacific[J]. Meteoro Atmos Phy, 121(3): 143-152. |
Jin Long, Yao Cai, Huang Xiaoyan, 2008. A nonlinear artificial intelligence ensemble prediction model for typhoon intensity[J]. Wea Forecasting, 136(12): 4541-4554. |
Kennedy, Eberhart, 1995. Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks[J]. IEEE Service Center, Piscataway, NJ: 1942-1948. |
Kwong K M, Wong M H Y, Liu J N K, et al, 2012. An artificial neural network with chaotic oscillator for wind shear alerting[J]. J Atmos Ocea Tech, 29(10): 1518-1531. DOI:10.1175/2011JTECHA1501.1 |
Lu Mong-Ming, Chu Pao-Shin, Lin Yun-Ching, 2010. Seasonal prediction of tropical cyclone activity near Taiwan using the Bayesian multivariate regression method[J]. Wea Forecasting, 25(6): 1780-1795. DOI:10.1175/2010WAF2222408.1 |
Manzato A, 2013. Hail in Northeast Italy: A neural network ensemble forecast using Sounding-Derived indices[J]. Wea Forecasting, 28(1): 3-28. DOI:10.1175/WAF-D-12-00034.1 |
Ritchie E A, Valliere-Kelley G, Pi eros M F, et al, 2012. Tropical cyclone intensity estimation in the North Atlantic Basin using an improved deviation angle variance technique[J]. Wea Forecasting, 27(5): 1264-1277. DOI:10.1175/WAF-D-11-00156.1 |
Roweis S T, Saul L K, 2000. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 290(5500): 2323-2326. DOI:10.1126/science.290.5500.2323 |
Rumelhart D E, Hinton G E, Williams R J, 1986. Learning representations by back-propagating errors[J]. Nature, 323: 533-536. DOI:10.1038/323533a0 |
Yu Hui, Chen Peiyan, Li Qingqing, et al, 2013. Current capability of operational numerical models in predicting tropical cyclone intensity in the Western North Pacific[J]. Wea Forecasting, 28(2): 353-367. DOI:10.1175/WAF-D-11-00100.1 |
 2014, Vol. 40
2014, Vol. 40 
