引言

短时强降水指短时间内出现的强度较大的降水，是由中尺度对流系统产生，在我国强对流天气预报业务中一般定义小时雨量超过20 mm的降水为短时强降水。短时强降水在短时间内可以造成暴洪、城市内涝等灾害，甚至可以引发泥石流和山洪等地质灾害，易造成重大的经济损失和人员伤亡。Yu等(2007a；2007b)对我国中东部地区小时降水的日变化特征进行了详细的分析研究，陈炯等(2013)对我国暖季短时强降水分布和日变化特征及其与MCS日变化关系进行了探讨。暴雨和短时强降水关系密切，尽管某些暴雨是由长时间的稳定性降水造成的，但对于我国而言，大多数暴雨都与短时强降水天气的出现有关，这是由我国夏季风演变的气候特征决定的(陶诗言，1980)。较多的研究工作针对暴雨、短时强降水的成因和相关的预报进行了分析(陶诗言，1980；方翀等，2012；慕建利等，2012；郝莹等，2012；仇娟娟等，2013)，这些研究成果为我国短时强降水天气的预报提供了基础。

对于我国华南、江南等地而言，20 mm·h^-1降水出现的频率相对较高(陈炯等，2013)，人们往往更关注更大强度的短时强降水，但对于其他地区，如西北等地形较为复杂的地区，20 mm·h^-1降水，甚至10 mm·h^-1强度的降水也可以造成较严重的局地泥石流等灾害。因此，对我国不同区域的小时降水强度气候分布特征进行更为详细的分析，对于了解我国不同区域短时强降水的阈值强度分布特征具有重要的意义。姚莉等(2009)通过频数分析方法对小时雨量超过1、2、4和8 mm情况下的时空分布特征进行了分析，指出较大雨强频数出现最多的地区夏季主要在南部沿海，春季在皖南和赣北，但对于更大强度的小时降水未做探讨。频率分析方法存在一些不足，有时会使得不同量级降水的频数分布产生不连续性，造成较大雨强的小时雨量出现的次数高于较小雨强的小时雨量出现的次数，且对于历史上无观测的降水强度等级缺乏描述能力，而这种极端(以前很少出现)事件相对于当地的气候统计特征具有极端性，往往易于造成重大的人员伤亡和经济损失。

通过分布函数研究降水强度的气候分布特征可以抓住其较为细微和普遍的变化规律，这是使用分布函数描述降水等气象相关物理量的气候形态分布的重要原因之一。通过分布函数还可以帮助确定不同地点极端降水出现的阈值，并可借助分布函数对无观测站点地区降水的分布进行研究。

由于降水、风速等物理量的取值范围的特点，它们的统计特征具有明显的不均匀性和偏态分布特征(Ison et al，1971；Wilks，1990；2006)。有多个分布函数可以描述具有这种分布特征的物理量，但对于降水而言，最具有代表性的是Γ分布函数(Wilks，2006)。水文上常用于暴雨重现期分析的皮尔逊Ⅲ型分布也是一种三参数的Γ分布。丁裕国(1994)研究指出，Γ分布可以用于描述不同累积时段降水的分布，Li等(1998)通过对我国1991年小时雨量资料的分析表明，Γ函数对我国的小时降水具有很好的描述能力。因此，本文将使用Γ分布函数获取观测站点小时降水量的概率密度分布函数，在此基础上对有降水情况下不同量级的小时降水量出现的累积概率进行分析，从而揭示小时降水强度的气候分布特征，从概率的角度揭示不同区域、不同强度小时降水量出现的可能性，从而为这些区域短时强降水强度阈值选取提供参考。

1 资料和方法 1.1 资料及其处理

本文所用资料为国家气象信息中心提供的经过质量控制的我国基本基准气象站整点观测小时降水资料，但未包含台湾省的资料。每个整点时次的记录为该整点时次之前1个小时的总降水量。由于各个站点观测的是非固态降水，因此资料中不同站点每年的时间跨度不同，南方全年有观测记录，北方地区多从5月开始至9月结束，这与我国暖季降水的出现季节一致。为了保证不同站点之间资料的一致性和可比性，剔除了记录开始日期晚于5月1日和(或)结束时段早于9月30日的站点，并对站点小时降水观测起始年份晚于1991年的站点进行了剔除。经过以上处理，最终所用资料为518个站点1991—2009年5月1日至9月30日的小时降水资料。总体而言，除西藏中西部大范围地区无观测站外，站点分布为从东南向西北逐渐稀疏(图 1)。

从各个站点的小时降水量来看，小时降水量超过0.1 mm的时次数在3900~12400 h；如果用小时雨量超过0.1 mm的次数与站点样本总量的比值表示降水出现的多寡，则从空间分布来看，以黄淮区域为界，南方地区的降雨时数是北方的两倍左右(图 2)，南方的降水高发区有3个显著的中心，其中四川盆地西南部为降水出现频次最多的地区，超过0.1 mm的时次数达到样本总量的24%，即大约每4个小时中就有1个小时出现了0.1 mm以上的降水，福建中东部和云南西部为另外2个降水高发区，小时雨量超过0.1 mm的小时数达到了18%，几乎每5个小时中就有1个小时有降水产生。内蒙古东部偏南地区超过0.1 mm的时次数百分比为5%，同周围区域相比降水频次显著偏低。这一分布与中国气候(张家诚等，1985)中揭示的我国年降水日数的分布特征非常一致。

1.2 Γ概率分布及其参数估计

Γ分布的概率密度函数为：

$\begin{align} &f(x)=\frac{{{(x/\beta )}^{\alpha -1}}\exp (-x/\beta )}{\beta \Gamma (\alpha )} \\ &x>0,\alpha >0,\beta >0 \\ \end{align}$

(1)

式中，α和β分别为形状参数和尺度参数，后文详细介绍其意义。Γ(α)为Γ函数，表达式为

$\Gamma (\alpha )={{\int_{0}^{\infty }{{{t}^{\alpha -1}}\text{e}}}^{-t}}\text{d}t$

(2)

可见，α是式(2) 的唯一变量，而式(1) 由α和β唯一确定，即一旦确定了α和β的值，Γ概率密度分布函数也将唯一确定，因此也可以计算对于给定降水阈值区间的累积概率P，P可以表示为：

$P(a\le x\le b)=\int_{a}^{b}{f(x)\text{d}x}$

(3)

则超过某一阈值b的累积概率可以表示为：

$\begin{align} & P(x\ge b)=\int_{b}^{+\infty }{f(x)\text{d}x}= \\ & \int_{a}^{+\infty }{f(x)\text{d}x}-\int_{a}^{b}{f(x)\text{d}x} \\ \end{align}$

(4)

其中 $\int_{a}^{+\infty }{f(x)\text{d}x}=1.0$ 。对于式(4)，如果知道了累积概率P和开始累积的下限a，反过来也可以通过式(4) 来求得上限b的值。

求取参数α和β的常用方法有矩估计法和最大似然估计法两种，但Thom(1958)和Wilks(1990)的研究表明，矩估计法不能充分利用所有的样本信息，且当α较小时，模拟结果严重偏离实际，建议使用最大似然估计方法来获得α和β的值。考虑到小时降水的分布中α一般较小，因此此处使用Thom(1958)提出的一种最大似然估计方法，即首先得到样本平均的自然对数与样本自然对数平均的差T，亦即样本算数平均和几何平均的自然对数之差，那么形状参数α可由Thom估计量得到，尺度参数亦可由式(7) 给出。由式(6) 和式(7) 可知，α的单位与所统计物理量相同，而β是无量纲的。式(5) 中n为各个站点小时雨量超过0.1 mm的总样本数。

$T=\ln (\bar{x})-\frac{1}{n}\sum\limits_{i=1}^{n}{\ln ({{x}_{i}})}$

(5)

$\alpha =\frac{1}{4T}(1+\sqrt{1+\frac{4T}{3}})$

(6)

$\beta =\frac{{\bar{x}}}{\alpha }$

(7)

2 参数分布特征

Γ分布的具体形状受控于形状参数α和尺度参数β。对于给定的尺度参数β，α越小，概率密度大值区越靠左，越接近0.0其概率密度越大，亦即右偏越显著，当x→0时f(x)→∞；当α=1时，f(0)=1/β；当α>1时，f(0)=0，即α越小，较小量级降水出现的概率越大。β之所以称为尺度参数，是因为它控制了分布函数曲线的拉伸和收缩程度，即对于给定的α，β越大，表明各个量级降水概率密度分布的分布越集中，而β越小，不同量级降水分布越分散。

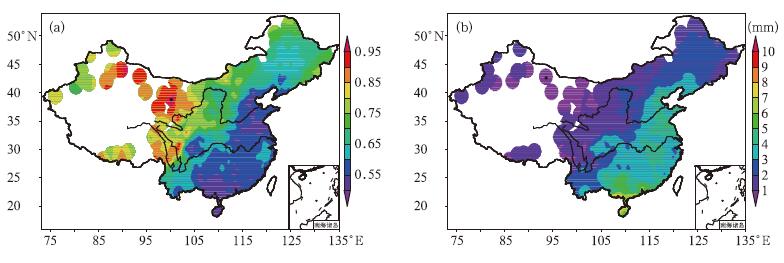
518个站点的形状参数α和尺度参数β的分布如图 3。整体而言，α值均小于1.0，且在0.5~1.0变化，表明小时雨量分布最常出现在雨量值较小的量级范围内。青藏高原东部和新疆西北部地区的α值一般在0.75~0.90，而中东部大部分地区的α值在0.50~0.70，α=0.7的等值线自黑龙江北部向西南伸展至云南北部，将我国的降水区显著地分为两部分，以东地区出现较强的小时降水的可能性显著大于西部地区。

尺度参数β的变化范围较大，其最小值为0.66，最大为8.49。整体而言，β自西北向东南逐渐增大，最大值出现在广西南部沿海。考虑形状参数α的变化特征可知，越往东南部地区，较高等级的小时降水出现的可能性越大，尤其是广西南部沿海。

由于形状参数α和尺度参数β在分布上自西北向东南的显著共同变化特征，对二者进行的拟合结果显示，二者服从非常好的指数函数分布(图 4)，随着形状参数α的增大，尺度参数β呈指数减小，拟合曲线的相关系数为0.975，表明对于描述我国小时降水分布的Γ函数而言，α和β的分布具有高相关性，在已知其中一个量的情况下，基本可以推测另一个量的分布，这对估算一些地区的降水分布是有利的，即在仅知道一个地区小时雨量均值的情况下，就可以根据式(7) 和图 4中的公式确定α和β的值，从而推算可能的小时降水的概率分布状况。

3 降水概率分布 3.1 站点降水概率分布

形状参数α和尺度参数β的分布决定了Γ分布，在得到站点的α和β值后，对模拟和实况之间的分布进行了对比，发现二者之间具有很好的一致性，表明计算得到的Γ分布很好地拟合了小时降水的概率分布特征。下面仅通过α取最大和最小值及β取最大和最小值时，4个站点的模拟概率分布与实况观测小时降水频率分布进行对比分析，4个站点的详细信息可以参见表 1，它们的位置可以参见图 3。图 5中灰色柱状图为实况观测降水的频率分布，黑色实线为根据α和β获得的Γ分布曲线，右上角的小图为各自对应的实况和模拟小时降水的累积概率密度分布曲线，其中图 5a~5d分别为最大α、最小α、最小β和最大β时的结果。在计算累计概率时，由于观测降水的间隔和最小记录为0.1 mm，因此实况降水的累积概率从0.1 mm开始，且频率统计中的间隔也为0.1 mm。而模拟可以给出任意间隔的降水累积，考虑计算精度的影响，仅从0.01 mm开始累加，且降水间隔取为0.001 mm。

根据前面讨论可知，形状参数α和尺度参数β之间具有很好的相关性，即较大的α往往对应较小的β。从图 5a和5c可知，最大α和最小β时两站的α和β均较接近，表明其小时降水分布均有很大的类似性。实况小时降水的频率分布和Γ适应函数分布曲线，两站的小时降水主要集中在5.0 mm以下的区间，且越接近0.1 mm出现的可能性越大。累积概率密度分布显示，模拟和实况之间均有非常好的一致性，且当降水达到阈值5.0 mm时，累积概率均已经超过了0.99，即99%以上的小时降水集中在5.0 mm以下的区域，这可能与两站均属于海拔较高的站点有关。因此，对于这两个站所代表的区域，其出现20.0 mm以上小时降水的概率也将非常小，也正是因为如此，当这些地区出现十几毫米的降水时，即为比较极端的短时强降水，易于对这些地区导致一定的灾害。

图 5b和5d所示为最小α和最大β时实况小时降水的频率分布和对应的Γ分布曲线。与图 5a和5c相比，图 5b和5d所示两站的Γ函数参数α和β具有很大的相似性，且降水分布也比较类似，尽管越靠近0.1 mm·h^-1降水出现的可能性越大，但较小量级降水的概率密度与图 5a和5c两站相比明显降低，同时较强量级降水出现的可能性在不断增加，部分降水甚至超过了50.0 mm。累积概率密度分布显示，20.0 mm阈值对应的累积概率为96%，此后累积概率增长的速度显著变缓，50.0 mm阈值降水对应的累积概率约为99%，但仍然有大约1%的概率超过50.0 mm，从而也表明，这些站点出现较强量级降水的可能性远大于图 5a和5c所代表的站点。实况和模拟累积概率分布也显示，由于实况降水的间隔限定在0.1 mm，模拟得到的累积概率密度分布具有更好的连续性，由于这种连续性，我们可以估计对于当前实况观测中未出现过的降水强度的概率，因此下文将对超过不同强度阈值的小时降水的可能性进行分析。

3.2 超过不同阈值的降水空间分布特征

由式(3) 和式(4) 可知，当降水的累积概率分布函数确定后，可以计算超过任意给定阈值的降水累积概率。为了从空间分布上对不同量级降水出现的可能性进行分析，对小时降水超过5.0、10.0、20.0和30.0 mm的累积概率进行分析。

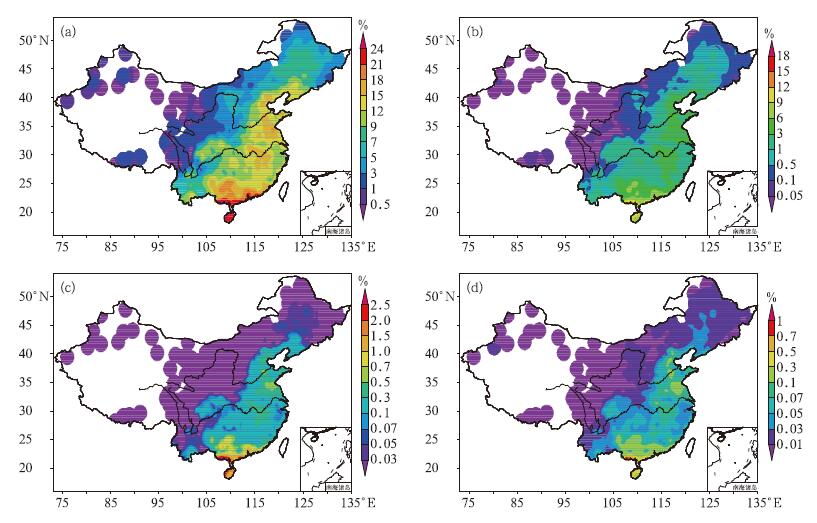
对于有记录时次小时雨量超过5.0 mm的累积概率空间分布而言，9.0%的累积概率等值线显著地将我国大陆地区分为两部分(图 6a)，笼统而言，中东部低海拔地区的累积概率显著大于西部高海拔地区，且越往东南出现5.0 mm降水的可能性越大，最大累计概率出现在华南南部沿海和海南，超过了21.0%，即所有超过0.1 mm的降水中，平均有21%的时次的降水量超过5.0 mm。相比于其他地区，整个华南地区均属于常出现5.0 mm以上降水的地区。与华南超过5.0 mm的较高累积概率相比，山东和江苏交界处也有一累积概率达到18%的地区，但大部分地区的累积概率在12%~18%，其次是江南中北部和环渤海周围。从9.0%等值线向西和向北，距离9.0%等值线越远，小时雨量超过5.0 mm的累积概率越小，高原地区仅为0.5%，如果定义超过95.0%的累积概率的降水为极端降水，则高原地区小时雨量达到5.0 mm已经是极端降水了。这种分布可能与海拔越高，空气柱越短，所能容纳的总的水汽量越少有关(Zhai et al, 1997)。

对于小时雨量超过10.0 mm的降水而言，其最常出现的地区仍然是广西东南部和海南西北部(图 6b)，最大累积概率超过了8.0%，即对于小时雨量超过0.1 mm的降水中，平均有8.0%以上的时次的小时降水量超过10.0 mm，即使如此，这一比例尚不足超过5.0 mm的概率的一半。小时雨量超过20.0和30.0 mm的累计概率分布与超过5.0和10.0 mm的累积概率分布相似，但对应的累积概率值一般小一个量级，最大累积概率值均出现在广西东南部和海南西北部，其中超过20.0和30.0 mm的累积概率分别为2.0%和0.7%，鲁苏皖交界处为华南南部沿海之外的另一个概率大值区，尽管结果与陈炯等(2013)得到的结果有一定的差异，但与图 3a所示形状参数α的分布非常一致，从而也揭示，尽管华北地区出现降水的小时数比较少，但容易出现量级较大的小时降水，这是短时强降水预报中需要注意的一点。同时，结合图 2所示的出现降水的比例可知，尽管四川盆地西南侧为降水出现频次最多的地区，但其出现大量级小时降水的可能性却较小，即这一地区虽然最容易出现降水，但以较小量级的降水为主，这也是在短时强降水预报中需要注意的一点。

3.3 极端降水的空间分布特征

由于极端降水的高致灾性和高影响性，很多情况下，人们更为关注极端降水的分布状况。许多学者(Garrett et al，2008a; 2008b; Gemmer et al, 2011)从概率分布的角度出发，定义超过某一累积概率阈值(一般为90%或95%)的事件为极端事件。本文中将小时雨量超过95%累积概率的雨量值定义为极端小时降水，则根据式(4) 可求得其对应的小时降水的阈值。图 7所示为根据式(4) 得到的95%累积概率密度对应的降水阈值的分布，其分布与小时雨量超过不同阈值的累积概率分布(图 6)一致，且与我国地形地势的分布(图 1)较为一致，95%累积概率对应的极端小时降水阈值自西北向东南逐渐增大，西北地区95%累积概率对应的极端小时降水阈值不超过5.0 mm，广西南部沿海超过了20.0 mm。华北平原和黄淮江淮地区95%累积概率对应的小时降水阈值高于江南大部，这也是短时强降水业务预报中需要注意的一点。

4 高海拔对分布形态的影响

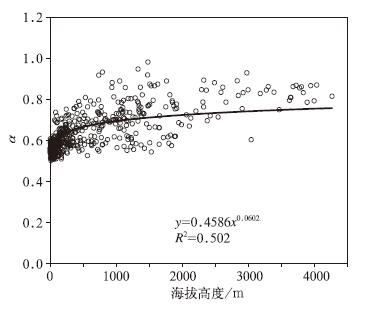
通过对比图 1和图 6可知，地形，尤其是海拔高度1000 m的等值线对不同等级降水的累积概率分布具有重要的影响，将其划分为显著的不同高低概率区域。而累积概率可以通过Γ分布中的形状参数α和尺度参数β唯一确定，地形是否对这两个参数有显著影响，需要通过分析来得到答案。考虑到α和β之间的指数分布关系，仅给出了α随海拔高度的变化。结果显示(图 8)，α与海拔高度呈指数相关，随着海拔高度的增高，α遵从指数规律单调递增，其R²超过了0.50。对于给定的β(β>1.0)，海拔越高，α越大，则出现较小量级小时降水的可能性越大，反之出现较大量级小时降水的可能性越大(图略)。可见，地形对于我国不同地区的小时降水分布具有非常重要的影响，这可能与地形对大气中的水汽含量所造成中尺度对流系统发生发展的动力热力条件都有影响有关，文中对此不做详细描述，对中小尺度的喇叭口地形等因素的影响也不做详细探讨。

5 结论

本文在对1991—2009年5月1日至9月30日的小时降水资料连续性进行处理的基础上，采用Thom(1958)所提出的最大似然估计方法，对用于拟合518个观测站点降水分布的Γ函数的形状参数α和尺度参数β进行了估算，Γ函数很好地描述了小时降水的概率分布特征，并可用于分析不同强度小时降水的概率分布。

通过站点概率密度函数分布及与实况观测频率的匹配，对极端α和β分布情况下降水的概率密度分布状况及其累积概率密度分布函数进行了模拟，并在此基础上给出了基于Γ函数的超过给定阈值的降水累积概率的分布。结果显示：

(1) 形状参数α和尺度参数β的分布均与我国的地形分布有很大的相关性，且α和β之间的相关性高达0.975，表明通过获取α和β的分布即可以确定用于描述某一点小时降水分布的Γ函数，从而给出其概率密度分布曲线；

(2) 通过极端α和β分布情况下模拟站点Γ分布与实况小时降水的频率分布相比可知，Γ函数分布很好地给出了小时降水分布的描述，根据Γ分布得到小时降水概率密度分布与实况一致，并可以对实况中未观测到的极端小时降水概率分布进行估计。

(3) 尽管四川盆地西南侧为出现0.1 mm小时降水时次最多的地方，但根据Γ函数得到的超过不同阈值的降水的累积概率密度表明，这一地区的降水主要集中在5.0 mm·h^-1以下，较强的小时降水主要集中在华南沿海和海南西北部，有降水记录(0.1 mm·h^-1以上)情况下其小时雨量超过10.0、20.0和30.0 mm的累积概率分布分别达到了8.0%、2.0%和0.7%，另一个常出现极端降水的区域为鲁苏皖交界处，这是强对流预报中值得注意的地方。

(4) α与海拔高度的关系显示，α与地形之间具有很好的指数相关性，其相关系数达到了0.709，因此结合(1) 可知，地形高度分布对我国小时降水的分布具有决定性的作用。

概率预报是我国强对流预报中面临的新任务，小时降水的概率分布研究是在观测资料基础上进一步开展工作的重要环节，因此，下一步将通过收集更长时效和更多站点的小时降水资料来对基于Γ分布的降水日变化特征进行分析，包括Γ分布的形状参数α和尺度参数β的日变化特征分析等，并进一步研究小时降水概率分布在短时强降水概率预报业务中的应用。