2. 中国气象科学研究院灾害天气国家重点实验室,北京 100081
2. State Key Laboratory of Severe Weather, Chinese Academy of Meteorological Sciences, Beijing 100081
天气过程中降水探测是多普勒天气雷达主要任务之一。多普勒天气雷达能实时估计雷达扫描范围内各点的雨强和一定区域上降水量的分布,并且可以及时获取大面积定量降水资料(张培昌等,2001)。
通常降水估测方法主要是基于单部雷达和雨量站联合进行的降水估测,并发展了多种单雷达和雨量站联合估测降水的方法和系统:变分法(Sasaki,1970;Ninomiya et al,1978)、Barnes客观分析方法(Brands,1975)、平均校准法(Wilson et al,1979)、卡尔曼(Kaman)滤波法(Ahnert et al,1986)、克里金(kriging)法(Krajewski,1987)、最优化校准法(Tanguay et al,1990)、最优插值法(Bhargava et al,1994)等。国内基于雷达联合雨量计的降水估测的研究也较多,例如:张培昌等(1992)、戴铁丕等(199b)、李建通等(1996)、林炳干等(1997)、官莉等(2004)、黄小玉等(2009)、彭涛等(2010)、东高红等(2012)、庄薇等(2013)、张亚萍等(2013)等。针对业务应用的降水估测系统主要有基于美国WSR-88D Precipitation Processing System(PPS)的Multisensory Precipitation Estimation(MPE)系统(Young et al,2000);刘晓阳等(2010)研发了基于新一代天气雷达的定量降水估测集成系统(QPEGS)。以上降水估测的方法和系统均是针对地面固定的单部雷达。肖艳娇等(2006)分析了单部雷达观测的很多局限,例如:探测范围小、静锥区、波速遮挡、波束展宽等,并提出了基于多雷达的三维组网拼图能很大程度上解决这些问题。肖艳娇等(2008)提出了基于雷达网的三维拼图反射率因子数据的混合反射率因子的获取是减小雷达波束受地物阻挡影响,提高雷达网降水估算精度的重要步骤之一。因此,在大范围降水估测中,先进行雷达数据的组网拼图,后进行降水估测,能减轻因单部雷达的局限而对降水估测精度造成的影响。
定量降水估测方法发展的同时,针对影响降水估测精度一些因素的分析也很多,如雨区衰减影响、回波强度垂直廓线(Vertical Profile of Reflectivity, VPR)影响、零度层亮带影响、雨滴谱引起的Z-R关系变化等。殷秀良等(2006)分析了各波段双偏振雷达各测雨式受雨区衰减的影响情况以及做衰减订正后的改进情况,可以使降水估测的精度不同程度改善。吴翠红等(2006)研究了用雷达回波强度垂直廓线订正雷达估算地面降水的技术,对进一步提高雷达定量测量降水有积极的意义。肖艳娇等(2010)提出新一代天气雷达反射率因子数据中亮带自动识别和抑制的算法,减轻了雷达反射率因子数据中零度层亮带污染对雷达降水估计的影响。赵果等(2011)指出传统的Z-R关系存在很多误差,最主要误差是Z-R关系随着雨滴谱的变化而变化,并分析了雨滴谱的地域差异较大,通过本地区的雨滴谱数据得到本地区降水强度的计算公式,从而提高降水估测的精度。上述是基于单部雷达降水估测精度影响因素的整体性分析,然而针对三维组网拼图数据提取出的混合扫描回波强度质量以及对降水估测影响的分析很少。用于大范围降水估测的区域混合扫描回波强度,其质量容易同时受下垫面、零度层亮带、回波强度垂直廓线等因素的影响,且目前针对影响因素而对混合扫描回波强度质量进行分区域的分析研究几乎没有。因此,对影响降水估测精度的几个因素进行分区域分析是很有必要的。
本文选取浙江地区进行了实际分析。首先进行雷达数据的组网拼图;其次利用中国气象科学研究院灾害天气国家重点实验室为杭州市气象局研发的雷达降水估测和临近降水预报系统中的降水估测部分(该系统先组网拼图后降水估测),进行了混合扫描高度的生成和降水量的反演(本文下面有详细介绍);最后用反演的降水量与雨量站的观测值进行对比分析,得到浙江及周边地区降水估测误差的实际分布情况。
1 基本情况介绍 1.1 数据的选取及处理2012年6月21—24日,受暖湿气流和弱冷空气共同影响,浙江省大部分地区出现了中到大雨,其中一些地区甚至出现暴雨。22日降雨带呈东西和南北两条带状分布,中后期降水主要集中在中南部和东南部,整个天气过程累积覆盖到浙江省全部区域及周边省的部分区域。由于该降水过程具有持续时间长、覆盖范围广、累积降雨量大等特征,所以选择该过程数据用于降水估测回波强度质量以及对降水估测影响因素的分析。雷达资料选取的是杭州、金华、舟山、衢州、宁波和温州6部新一代天气雷达的原始体扫数据。雷达数据选用6月22日02时到6月24日12时(UTC,下同),时长为58 h的3486个体扫数据。
在利用雷达资料进行分析之前,需要进行一些处理:首先,采用中国气象科学研究院灾害天气国家重点实验室开发的雷达基数据资料杂波抑制程序,对原始体扫基数据进行一些必要的质量控制(刘黎平等,1996;2007)。其次,利用中国气象科学研究院灾害天气国家重点实验室研发的新一代天气雷达三维组网拼图软件(王红艳等,2009),采用NVI方法(肖艳娇等,2008)将各个雷达站的体扫资料数据插值到三维格点上。最后,将各单雷达站的三维格点数据进行三维组网拼图处理,得到浙江及周边地区的三维格点的回波强度数据。
雨量站资料为全国1 min自动雨量站数据。在进行降水回波强度质量分析时,需要在全国雨量站数据中提取出相应6部雷达组网拼图区域(26.5°~32.0°N、117.0°~123.0°E)内的雨量站。
1.2 浙江地区地物遮挡和混合扫描高度浙江地区的地形较为复杂,给降水估测精度造成了一定的影响。金华雷达西北面和东北面受到离雷达较近地物的完全遮挡,在组网拼图时2 km以上的回波强度数据主要是由杭州雷达来填补。衢州雷达东北面同样也受到离其较近地物的部分遮挡和完全遮挡,并与金华雷达西北面的部分遮挡区有重叠,部分缺失的数据由高一层数据和金华雷达数据填补。其余4部雷达没有受到地物遮挡。
本文对影响浙江地区降水估测精度几个要素的分析,基于中国气象科学研究院灾害天气国家重点实验室开发并且在杭州市气象局业务运行的降水估测和临近降水预报系统。该系统基于浙江地区的地形,通过几次天气过程的训练,生成一个固定的混合扫描高度。具体方法是:首先,根据浙江及周边地区的地形情况,限定用于降水估测的混合反射率因子在2.5~4.0 km的高度层;其次,在限定高度层的范围之中,分别找出每个水平格点在垂直方向上高度层最低且有效(最小阈值10 dBz,最大阈值70 dBz)的反射率因子,记录下该反射率因子所在的高度层,将所有格点的高度组合起来就得到了单个组网拼图数据的最低有效高度层数据;最后,通过几次覆盖组网拼图区域的天气过程生成最低有效高度层数据集,对应找出每个格点在所有最低高度层数据集中的最低有效高度层,便得到浙江等地区固定的最低有效高度,即固定的混合扫描高度(如图 1c)。用于降水估测的混合反射率因子是根据固定的混合扫描高度取得。
|
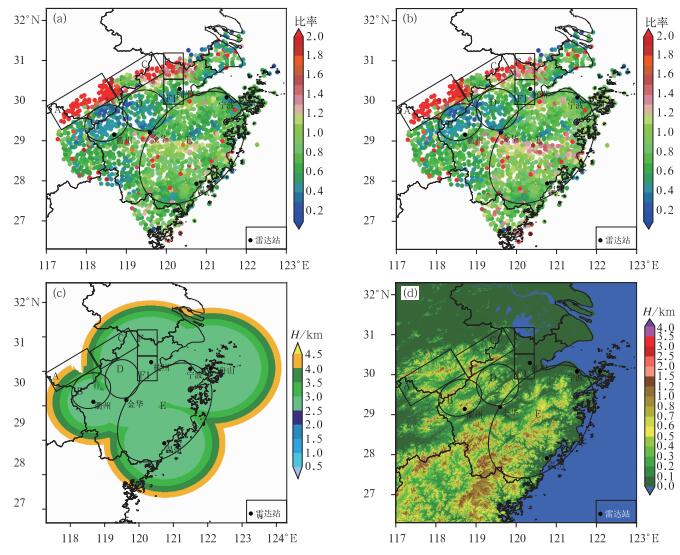
图 1 (a)固定Z-R关系下比率的空间分布,(b)动态拟合Z-R关系下比率的空间分布, (c)混合扫描高度 (单位:km),(d)浙江地区数字高程模型(单位:km) [数字高程模型(DEM)源于中国科学院计算机网络信息中心国际科学数据镜像网站(http://datamirror.csdb.cn)] Fig. 1 (a) Spatial distribution of the ratio with fixed Z-R relationship, (b) spatial distribution of the ratio with dynamic fitting Z-R relationship, (c) hybrid scan height (unit: km), (d) digital elevation model (DEM) in Zhejiang Province and the surrounding areas (unit: km) [The data set is provided by International Scientific and Technical Data Mirror Site, Computer Network Information Centre, Chinese Academy of Sciences (http://datamirror.csdb.cn)] |
分析三维组网拼图数据提取出的混合反射率因子质量好坏,首先就需要将混合反射率因子通过一定的方法反演成降水量。本文使用了三种降水量反演的方法:固定Z-R关系法(Z=200R1.6)、动态拟合Z-R关系法和雷达雨量站联合法。其中雷达雨量站联合法需要将该区域的雨量站均匀分为两部分,一部分用于订正,另一部分用于验证分析(具体分类标准和结果见第4节和图 7a)。联合法主要分为两步:首先,使用动态拟合Z-R关系得到的降水场作为雷达雨量站联合反演降水的初值场;其次,用一部分雨量站对雷达的初值场进行订正得到最后的降水场,订正方法为最优插值法(李建通等,1996;公式略)。
|
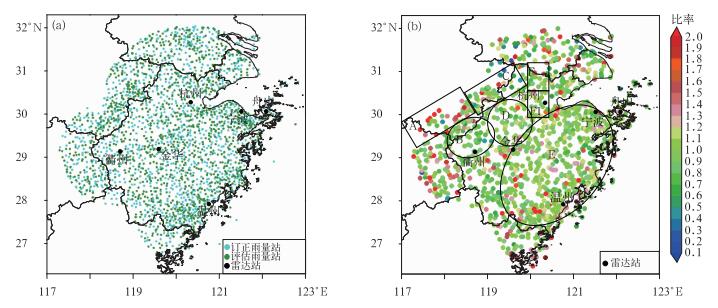
图 7 (a)雷达三维拼图范围内评估和订正雨量站的分布(青色点为评估雨量站,蓝色点为订正雨量站),(b)动态拟合Z-R关系反演的雷达初值场订正后的比率分布 Fig. 7 (a) The distribution of rainfall stations for assessing and correcting in the 3-D mosaic areas(cyan point is the rainfall station for assessing, blue point is the rainfall station for correcting), (b) the distribution of ratio got by corrected radar initial field with dynamic fitting Z-R relationship |
分析方法采用的是雷达估测降水和对应雨量站观测值的比率。主要是指:每个雷达-雨量站对随时间分别进行雨量的累加(参与累加的雨量大于0.1 mm);将累加的雨量对比,便得到了每个点比率 ;因此,将所有比率点组合在一起就得到了组网区域内降水量的比率分布。当比率值在1.0及其附近时,混合反射率因子和雨量站观测值的质量均较好;当比率值距离1.0较远时,混合反射率因子或者雨量站观测值的质量(雨量站质量可以从周围的比率对比判断出)较差。从组网拼图整个地区的比率可以发现较为规律的高估(比率大于1.0)和低估(比率小于1.0)分布,并且较直观地体现了雷达探测资料和雨量站资料的质量问题。
单点比率计算的公式:
| ${{B}_{i}}=\frac{\sum\limits_{n=0}^{N}{{{R}_{i}}(n)}}{\sum\limits_{n=0}^{N}{{{G}_{i}}(n)}}$ | (1) |
式中,i为第i个评估雨量站,n为第n个时次的数据,Ri(n)为i个评估雨量站对应上空的混合反射率因子用其中一种方法反演的降水量,Gi(n)为评估雨量站观测的雨量,N为参与分析数据的总量。
3 实例分析利用第1节中选取出来并处理过的雷达和雨量站数据,分析降水估测的混合扫描回波强度质量以及对降水估测的影响。反演降水的方法采用了固定Z-R关系和动态拟合Z-R关系,如图 1a和1b为固定Z-R关系法和动态拟合Z-R关系法估测降水量与雨量站观测降水量的比率空间分布。根据比率的空间分布规律及几种影响回波强度质量的因素,将浙江及周边地区分为6个小区域,分别为A、B、C、D、E、F(其中F1区作为F区的对比区域)。6个区域的特征为:在A区域,呈现了整片雷达混合扫描回波强度高估的特征;在B和D区域,呈现了整体混合扫描回波强度低估特征;在C区域,呈现了两端混合扫描回波强度高估而中间估测合理的特征;在范围较大的E区域,呈现了混合扫描回波强度估测较为合理的特征;在F区域,呈现了混合扫描回波强度随纬度增加而高估的特征。本文下面将分小节对造成区域性高估或低估进行详细的分析。
3.1 A区域分析A区域分布的比率大部分大于2(图 1a和1b)。该区域混合反射率因子普遍在3 km以上,探测的边缘地区达到了4 km高度(图 1c),由地形高度(图 1d)可知该区的海拔高度最高不超过2 km,其余大部分1 km以下,排除地物杂波引起的高估。
因此,进一步分析该区一段时间内的混合反射率因子(如图 2a~2f),其值普遍在30~45 dBz范围内,随着混合扫描高度层越高混合反射率因子越大。夏季我国中纬度地区0℃层亮带一般出现在3~5 km高度(有时会超过5 km)(仲凌志等,2007)。可以断定该区域整体比率值较大(即用于降水估测的混合扫描回波强度过大),是由于0℃层亮带污染造成。因此,在进行降水估测时,混合反射率因子应该尽量避免0℃层亮带的干扰,可以在允许的情况下缩小降水估测的范围(离雷达越远的探测边缘地区,用于降水估测的混合反射率因子所在的高度层就越高)。

|
图 2 2012年6月22日02:00—07:00 A区降水估测所用的混合反射率因子(单位:dBz) Fig. 2 Hybrid reflectivity for precipitation estimation of region A, during 02:00-07:00 UTC 22 June 2012(unit:dBz) |
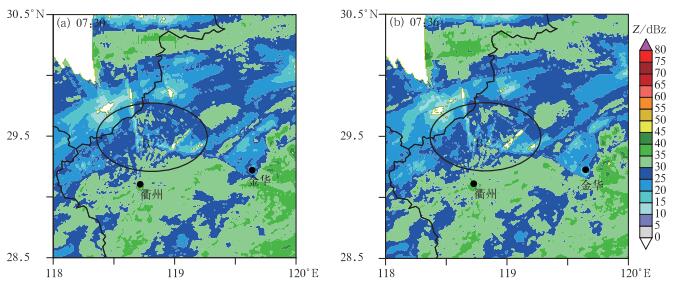
B区域分布的比率较低,大部分低估严重。在混合扫描高度图中(图 1c),该区域部分混合反射率因子所在高度层较高。观察其混合反射率因子(图 3a和3b)可知,B区域主要是由金华和衢州雷达探测时部分地物遮挡导致回波强度较弱,从而造成了降水估测的低估。
|
图 3 2012年6月22日07:30(a)和07:36(b)B区降水估测所用的混合反射率因子(单位:dBz) Fig. 3 Hybrid reflectivity factors for precipitation estimation of region B during (a) 07:30 and (b) 07:36 UTC 22 June 2012 (unit:dBz) |
C区域为复杂地形区,该区域主要是由杭州雷达覆盖。从比率分布(图 1a和1b)可知,区域中间比率较为合理,左右两边明显呈现高估,并和该区的地形高度(图 1d)较为吻合。区域混合反射率因子高度在2.5 km,部分地形高度达到了2 km,所以区域两边高估带主要是由于杭州雷达探测时混入了部分的地物杂波。由于区域中间地形高度 较低,形状像“凹”,雷达探测时并没有混入地物杂波,所以区域中间用于降水估测的混合扫描回波强度质量较好。
3.4 D区域分析D区域可由混合反射率因子直接反映出(图 4a和4b),在金华雷达附近有一条明显差异线,线的左下混合反射率因子值明显较大,右上明显较弱。金华雷达的海拔高度在1.2 km左右,杭州雷达的海拔为96 m。因此,相比于其他雷达,混合反射率因子较小的部分主要是由杭州雷达探测到的,低估带的分布主要是离杭州雷达越远其低估越为严重。其原因主要是:由杭州雷达本身问题造成,并且浙江地区在进行三维组网拼图时没有进行反射率差异分析,所以致使降水估测低估。由此可知,在进行组网拼图时对多雷达同步探测的反射率差异进行分析是必要的,雷达定期的检修与标定,是保证探测数据准确的前提。

|
图 4 2012年6月22日06:48(a)和06:54(b)D区域的混合反射率因子 Fig. 4 Hybrid reflectivity factors for precipitation estimation of region D during (a) 06:48 and (b) 06:54 UTC 22 June 2012 |
E区域为雷达的重叠覆盖区,该区分布的比率大多数在1.0附近。固定Z-R关系和动态拟合Z-R关系反演的降水均能达到较理想的效果(图 1a和1b)。由此可知,区域雷达的密度或雷达重叠扫描的次数越多三维组网拼图得到的反射率因子就更为准确,用于降水估测的混合扫描回波强度质量就越好。
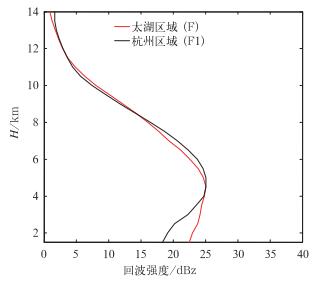
3.6 F区域分析图 1a~1d中的F区域(太湖区域)北面为太湖,在此区域可以发现比率至下到上(按纬度)逐渐增大,在太湖边缘地区达到最大。如图 1c该区域用于降水估测的混合反射率因子高度在2.5 km,并且此处地势较为平坦,海拔高度普遍低于100 m,所以该区的高估不是由混入地物杂波造成的。为了分析其原因,找了另一个区域F1(杭州区域),进行F和F1区域平均法的反射率因子垂直廓线(MVPR)对比。MVPR具体方法为:首先,利用三维组网拼图各高度层的反射率因子数据,分别对F和F1区域分层求取反射率因子的平均值,需要处理数据的时间为2012年06月22日02:00—10:00,共8 h;其次,将各高度层上两个区域的平均反射率因子数据在上述时间段内进行累加;最后,将两个区域各层上8 h平均反射率因子累加量再次求平均,便得到了F和F1的MVPR。1.5 km高度层的反射率因子数据能大概将F区域覆盖,所以统计高度层1.5~14 km。F、F1区域的反射率因子垂直廓线如图 5。
|
图 5 2012年06月22日02:00—10:00F和F1区域回波强度垂直廓线 Fig. 5 Vertical profiles of echo intensity in regions F and F1 during 02:00—10:00 UTC 22 June 2012 |
F1区域在4 km随高度减小反射率因子迅速变小,在2 km高度时减小到20 dBz以下,然而F区域的反射率因子在4 km以下变化缓慢,在1.5 km高度时反射率因子值为23 dBz左右。两个区域用于降水估测的混合反射率因子在同一高度层上(2.5 km),F区域的混合反射率因子值明显高于F1区域。异常的回波强度垂直廓线,导致了F区域的回波强度高估。
3.7 其余异常比率点的分析在整个研究的区域中,除去A、B和F整片的高估区,还零散的分布着一些异常比率点(其比率值大于2.0),并与周围点的比率值相差较大(图 1a和1b)。在异常的比率点中(图 6a),任意选取3个点分别进行雨量站观测值的降水强度以及对应雷达资料反演的降水强度随时间变化的分析(时间长度为选取的整个天气过程),其中雷达资料反演降水强度方法同样为固定Z-R关系法和动态拟合Z-R关系法。如图 6a三角形中的站号为K9133、椭圆中的站号为K4042和正方形中的站号为K3226,结果发现:自动雨量站的数据质量较差,是造成零散异常点的主要原因。这些质量较差的雨量站通常部分时间段的数据缺测严重,泥沙的影响导致采集到的数据远小于该点本身的降雨量,雨量站自身出现了故障等。

|
图 6 (a)零散的异常比率点,(b)、(c)和(d) 站号分别为K9133、K4042和K3226雨量站与对应两种方法每个时次降水强度的分布 Fig. 6 (a) The scattered points of abnormal ratio; (b), (c), (d) the hourly precipitation intensity distribution of rainfall station (station number: K9133, K4042, K3226) and the corresponding two methods |
用自动雨量站对动态拟合Z-R关系得到的降水估测初值场进行订正。将该区域内的全部雨量站分为两部分:一部分用于该区域降水估测的订正,订正采用的是最优插值法;另一部分用于订正后的评 估,同样是用单点的比率评估。具体分类标准:首先,统计出雷达三维拼图范围内的所有雨量站;其次,将雨量站按经纬度从下到上、从左到右顺序排列;最后,将雨量站的序列号对2取余,余数为0的分为评估雨量站组,余数为1的分为订正雨量站组。分类结果如图 7a,其中青色点为评估的雨量站,蓝色点为订正雨量站。雷达初值场通过自动雨量站的订正得到该区域降水量,然后利用订正后降水场和评估雨量站的观测值就可以得到比率分布(图 7b)。
将上述得到的比率和动态拟合Z-R关系下反演的降水量与全部雨量站观测降水量的比率(图 1b),没有经过雨量站订正)作对比,可以发现:A区域的高估点得到了一定程度的缓解,但是雷达探测的边缘部分并没有得到很好抑制,主要原因是由于最优插值法的局限:订正雨量站位于区域边界一侧会造成较大误差(李建通等,2000);在B和D区域,大部分的低估得到较好的缓解,但是B区域的中东部还是有几个不是很严重的低估点,原因是这几个低估点位于低估区域的中间(D区域的西部低估较为严重),利用周围雷达雨量站对的最优插值法进行订正误差较大,使其订正效果不佳;在C和F区域,高估的部分几乎被抑制,其中C区域的中部和F区域的北部还是有极少点高估,其原因同A区域;在E区域,经过部分雨量站的订正,其比率更加合理。在整个区域比率相比于图 1a其高估点增多(排除3.7节中已确定的异常点),其原因主要有:最优插值法的局限、雨量站质量较差(包括:部分时段缺测和泥沙影响)、降水空间结构场的不均匀性、在进行比率计算时雷达雨量站对的雨量累积次数较少不具代表性等。造成高估点增多的原因较多且复杂,还需要今后进行更深层次研究,本文就不再进行详细的分析。
5 结论在利用雷达三维拼图数据进行降水估测中,如何提取用于降水估测的回波强度是提高降水估测精度的关键。本文根据杭州市气象局运行的降水估测系统,得到浙江地区固定的混合扫描高度,并通过混合扫描高度提取到了用于降水估测的回波强度。混合扫描回波强度质量很大程度上影响了降水估测的精度,通过对其质量的分析可以得出以下结论:
(1) 由于0℃层亮带的影响,致使用于降水估测的回波强度过高,从而导致该地区降水估测严重高估。
(2) 在金华和衢州雷达北面,由于在离雷达较近的地方受到部分地物遮挡和完全遮挡,使探测到的回波较弱,导致该区域降水估测严重低估。
(3) 在复杂地形区域,尽管进行了地形杂波的控制,但是部分混在降水回波中地物杂波仍没有办法将其消除,造成了C区域的比率大小随地形的分布,其分布像“凹”形。
(4) 由于杭州雷达本身的问题,造成了其探测范围内的回波较弱,使D区域降水估测偏低。
(5) 在三维组网中,E区域为雷达重叠扫描区,当雷达密度越大或者重叠扫描的次数越多,区域内三维组网拼图得到的反射率因子就更为精确,用于降水估测的回波强度质量就越好。
(6) 异常的回波强度垂直廓线是造成太湖地区高估的直接原因,但是造成回波强度垂直廓线异常的原因,还需要进一步的研究工作。
(7) 整个区域中零散的异常比率点主要是由于雨量站的质量较差造成的。
(8) 用部分雨量站对动态拟合Z-R关系得到的降水初值场进行订正,能部分缓解各区域的高估或低估,但是部分区域降水估测评估的比率仍然不理想。
由于目前收集得到的大范围降水例子较少,用一个过程来分析检验略显不足,某些影响因素还需要进一步验证。
戴铁丕, 詹煜, 刘玉洁, 1996. 在雷达-雨量计联合探测系统中距离加权和时间外推校准技术的研究[J]. 气象科学, 16(1): 63-74. |
东高红, 刘黎平, 2012. 雨量计密度对校准雷达估测降水的影响及单点对校准的贡献[J]. 气象, 38(9): 1042-1052. |
官莉, 王振会, 裴晓芳, 2004. 雷达估测降水集成方法及其效果比较[J]. 气象科学, 24(1): 104-111. |
黄小玉, 陈媛, 熊毅, 等, 2009. 漂移克里金方法在雷达和雨量计联合估测降水中的应用[J]. 气象学报, 67(2): 288-297. DOI:10.11676/qxxb2009.029 |
李建通, 杨维生, 郭林, 等, 2000. 提高最优插值法测量区域降水量精度的探讨[J]. 大气科学, 24(2): 263-270. |
李建通, 张培昌, 1996. 最优插值法用于天气雷达测定区域降水量[J]. 台湾海峡, 15(3): 255-259. |
林炳干, 张培昌, 顾松山, 1997. 天气雷达测定区域降水量方法的改进与比较[J]. 南京气象学院学报, 20(3): 334-340. |
刘黎平, 王致君, 1996. 双线偏振雷达探测的云和地物回波的特性及其识别方法[J]. 高原气象, 15(3): 303-310. |
刘黎平, 吴林林, 杨引明, 2007. 基于模糊逻辑的分步式超折射地物回波识别方法的建立和效果分析[J]. 气象学报, 65(2): 252-260. DOI:10.11676/qxxb2007.024 |
刘晓阳, 杨洪平, 李建通, 等, 2010. 新一代天气雷达定量估测降水估测集成系统[J]. 气象, 36(4): 90-95. DOI:10.7519/j.issn.1000-0526.2010.04.016 |
彭涛, 宋星原, 殷志远, 等, 2010. 雷达定量降水估算在水文模式汛期洪水预报中的应用试验[J]. 气象, 36(12): 50-55. DOI:10.7519/j.issn.1000-0526.2010.12.007 |
王红艳, 刘黎平, 肖艳娇, 等, 2009. 新一代天气雷达三维数字组网软件系统设计与实现[J]. 气象, 35(6): 13-18. DOI:10.7519/j.issn.1000-0526.2009.06.002 |
吴翠红, 万玉发, 吴涛, 等, 2006. 雷达回波垂直廓线及其生成方法[J]. 应用气象学报, 17(2): 232-239. DOI:10.11898/1001-7313.20060215 |
肖艳姣, 刘黎平, 2006. 新一代天气雷达网资料的三维格点化及拼图方法研究[J]. 气象学报, 64(5): 647-657. DOI:10.11676/qxxb2006.063 |
肖艳姣, 刘黎平, 李中华, 等, 2010. 雷达反射率因子数据中的亮带自动识别和抑制[J]. 高原气象, 29(1): 197-205. |
肖艳姣, 刘黎平, 杨洪平, 2008. 基于天气雷达网三维拼图的混合反射率因子生成技术[J]. 气象学报, 66(3): 470-473. DOI:10.11676/qxxb2008.043 |
殷秀良, 孙成志, 袁群哲, 等, 2006. 雨区衰减对双线偏振雷达测雨的影响研究[J]. 南京气象学院学报, 29(3): 402-407. |
张 培昌, 杜 秉玉, 戴 铁丕, 2001. 雷达气象学[M].
北京: 北京气象出版社, 499.
|
张培昌, 戴铁丕, 傅德胜, 等, 1992. 用变分方法校准数字化天气雷达测定区域降水量基本原理和精度[J]. 大气科学, 16(2): 248-256. |
张亚萍, 张勇, 廖峻, 等, 2013. 天气雷达定量降水估测不同校准方法的比较与应用[J]. 气象, 39(7): 923-929. DOI:10.7519/j.issn.1000-0526.2013.07.013 |
赵果, 楚荣忠, 张彤, 等, 2011. 偏振多普勒雷达定量测量降雨精度的改进[J]. 高原气象, 30(2): 498-507. |
仲凌志, 刘黎平, 顾松山, 2007. 层状云和对流云的雷达识别及在估测雨量中的应用[J]. 高原气象, 26(3): 593-602. |
庄薇, 刘黎平, 胡志群, 2013. 青藏高原零度层亮带的识别订正方法及在雷达估测降水中的应用[J]. 气象, 39(8): 1004-1013. DOI:10.7519/j.issn.1000-0526.2013.08.007 |
https://link.springer.com/article/10.1007/s00376-011-1139-8Ahnert P R, Krajewski W F, Johnson E R. 1986. Kalman filter estimation of radar-rainfall field bias//Preprints, 23rd Conf on Radar Meteorology, AMS, 33-37.
|
Bhargava M, Danard M, 1994. Application of optimum interpolation to the analysis of precipitation in complex terrain[J]. J Appl Meteor, 33: 508-518. DOI:10.1175/1520-0450(1994)033<0508:AOOITT>2.0.CO;2 |
Brands E, 1975. Optimizing rainfall estimates with the aid of radar[J]. J Appl Meteor, 14: 1339-1345. DOI:10.1175/1520-0450(1975)014<1339:OREWTA>2.0.CO;2 |
Krajewski W F, 1987. Cokriging radar-rainfall and rain gauge data[J]. J Geophys Res, 92: 9571-9580. DOI:10.1029/JD092iD08p09571 |
Ninomiya K, Akiyama T, 1978. Objective analysis of heavy rainfalls based on radar and gauge measurement[J]. J Meteor Soc Japan, 50: 206-210. |
Sasaki Y, 1970. Some basic formalisms in numerical variation analysis[J]. Mon Wea Rev, 98: 875-883. DOI:10.1175/1520-0493(1970)098<0875:SBFINV>2.3.CO;2 |
Tanguay M, Robert A, 1990. An efficient optimum interpolation analysis scheme[J]. Atmos Ocean, 28: 365-377. DOI:10.1080/07055900.1990.9649383 |
Wilson J W, Brandes E A, 1979. Radar measurement of rainfall-A summary[J]. Bull Amer Meteor Soc, 60(9): 1048-1058. DOI:10.1175/1520-0477(1979)060<1048:RMORS>2.0.CO;2 |
Young C B, Bradley A A, Krajewski W F, et al, 2000. Evaluating NEXRAD multisensor precipitation estimates for operational hydrologic forecasting[J]. J Hydrometeor, (1): 241-254. |
 2014, Vol. 40
2014, Vol. 40 