引言

目前，随着数值预报技术的飞速发展，数值预报产品在各级气象台站发挥着越来越重要的作用(杜钧等，2014)，然而，由于数值模式初值和模式自身存在的误差，导致数值预报产品存在着一定的误差，因此，采用一定的释用方法对数值模式直接输出的产品进行处理，从而改进总体预报效果，是目前国际上通行的做法。释用技术一直伴随模式技术的发展而发展，其主要方法包括：统计学释用模式输出统计(Model Output Statistics, MOS)法、完全预报(Perfect Prognostic, PP)法和卡尔曼滤波(Kalman Filter, KF)法、天气学释用、动力学释用和人工释用等(朱盛明等，1988)，释用对象随模式预报能力的进步也由最初通过对天气形势的订正与细化来推定要素预报的“天气尺度释用”，转向对具体天气要素订正与提高的“中尺度释用”(薛纪善，2007)。一些主要业务预报系统开展的针对气象要素的订正与释用，明显提高了模式要素预报的精度(马清等，2008；王迎春等，2002；邓国等，2010；李莉等，2011；陈朝平等，2010；陈法敬等，2011)。降水是预报员日常最为关注的一种天气要素，李莉等(2006)采用频率匹配的方法对T213降水预报进行了订正，结果表明该方法对T213降水预报的偏差有明显改善。但该文的重点是讨论累积观测值和预报值样本的不同方法如递减平均法和标准正态分布法以及不同分区和样本时段长度对结果的敏感性，没有详细介绍降水频率匹配方法的原理及实现过程，在结合订正原理对所得结果原因的分析方面着笔不多。为了使更多的人在实际业务预报中了解和应用此法，本文着重介绍此法的原理和实现方法，并深入分析其优缺点和注意事项以便改进，同时根据此法的原理深入探讨所见现象的原因, 并有针对性地提出可以改进和尝试的方法。

自2006年以来，为了推动我国数值预报业务的发展，由中国气象局数值预报中心牵头，开展了8个区域气象中心区域模式统一检验业务平台的建设工作，中国气象局武汉暴雨研究所运行的AREM模式(宇如聪等，2004)作为华中区域模式参加了统一检验和评估工作。本文基于AREM模式降水预报产品，开展降水偏差订正研究，重点介绍降水频率或面积的匹配方法的基本原理及其实现过程，并对订正试验的效果进行了分析，以期为进行降水偏差订正的相关科研和业务工作提供借鉴。

1 AREM模式、降水误差特征及检验方法简介

华中区域中心采用我国科学家自主发展的AREM模式，水平分辨率15 km，垂直分辨率42层，模式层顶10 hPa，预报区域15°~55°N, 70°~135°E，选用显式暖云微物理过程，非局地边界层方案，多层结通量-廓线的地表参数化方案以及基于Benjamin理论的地表辐射参数化方案等。

2011年国家气象中心采用统一检验平台对AREM模式全年的预报进行了检验(Chen et al, 2013)，降水检验区域为全国范围2510站，检验的降水为24 h累积量。AREM模式1和2 d的晴雨预报准确率分别为66%和68%，中雨的偏差(BIAS)评分24和48 h预报分别为2.8和2.7。在此，降水偏差(BIAS)定义的是降水区范围的偏差即预报降 水面积(F)与实况降水面积(O)之比, 而不是降水量的偏差, BIAS=1表示二者面积相等, >1表示预报面积偏大(湿偏差), ﹤1表示预报面积偏小(干偏差)。中雨的漏报率分别为44%和54%，而两个时段的空报率则达到了72%，空报明显大于漏报，表明AREM模式降水预报具有明显的湿偏差。针对以上情况，开展了针对AREM模式降水预报的偏差订正工作。

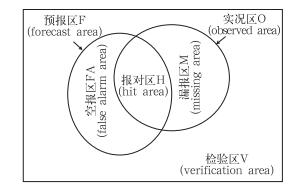
为了方便讨论和读者阅读，我们把本文所用各种检验方法的意义和公式罗列如下(图 1和式1~8):

$BIAS=\frac{F}{O}$

(1)

$平均误差=\frac{1}{V}\sum\limits_{i=1}^{v}{({{f}_{i}}-{{o}_{i}})}$

(2)

$绝对误差=\frac{1}{V}\sum\limits_{i=1}^{v}{\left| {{f}_{i}}-{{o}_{i}} \right|}$

(3)

$空报率=\frac{FA}{F}$

(4)

$漏报率=\frac{M}{O}$

(5)

$晴雨准确率=\frac{V-FA-M}{V}$

(6a)

$降水准确率=\frac{H}{O}$

(6b)

$TS=\frac{H}{FA+H+M}$

(7)

$ETS=\frac{H-R}{FA+H+M-R}$

(8)

式中，f是预报值，o是观测值，F是预报区，O是实况区，H是报对区，FA是空报区，M是漏报区，V是检验区，R=F×O/V是随机碰运气报对的可能性(这类似于某事件在气候背景中出现的频率，在严格的评分中如ETS这一部分应该去掉)。

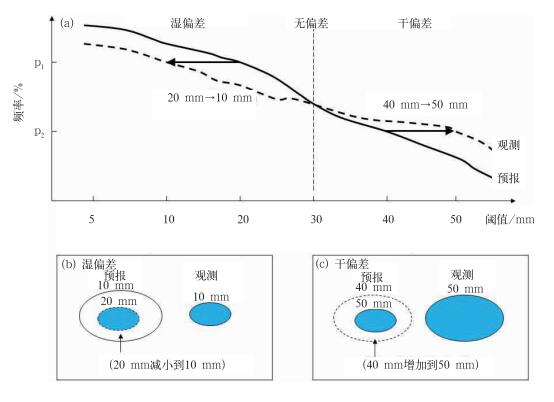
2 订正降水的频率或面积匹配方法 2.1 基本原理和实现方法

本方法的基本原理可用图 2来描述。图 2a表示通过统计预报和实况前期在不同阈值条件下降水出现的频率(可以是空间上的或时间上的或二者兼用)的示意图, 可以看到小的降水报得太多(湿偏差)而大的降水却太少(干偏差)。针对某一阈值，假定它在预报中出现的频率应该同实况中出现的频率一致(即纵坐标值保持不变)，那么预报中的20 mm降水应该被订正到同实况一致的10 mm降水量；同理，40 mm的预报降水应被订正到50 mm降水量。这种保持出现频率一致的方法可称为“频率匹配法”。如从空间上的分布来理解(图 2b和2c)，频率的大小实际上就是空间范围的大小(站点或格点数的多少)。这样，在湿偏差情况下某一量级，如10 mm 以上的预报面积大于实况的面积(图 2b)，这时如果20 mm以上的预报雨区恰同实况的10 mm以上的雨区面积相当，那么在“预报面积应该同实况 面积一致”的假定下，预报中的20 mm降水应该被降到同实况面积一致的10 mm降水量；同理，在干偏差情况下(图 2c)40 mm的预报降水应被提高到50 mm降水量。所以“频率匹配法”也可称为“面积匹配法”, 因为此法考虑了预报和实况雨区面积的一致性。

具体实施则是根据预报和观测频率的两组前期统计数据(图 2a)，采用多项式插值的方法对它们进行曲线拟合、获得不同阈值模式降水预报的转换系数，即将模式降水预报的频率分布曲线调整到与观测降水频率分布曲线一致，这样利用所获得的转换系数从而达到订正预报降水偏差的目的。前期的预报和实况频率的统计有各种不同的做法，如李莉等(2006)采用的递减平均法、讨论过的标准正态分布法以及本文所用的过去20 d的滑动平均法。关于阈值选取和平均天数确定的讨论可以参考李莉等(2006)的工作，较理想的是根据本地降水分布的气候特征调整降水阈值的选取范围，根据天气变化的剧烈程度调整计算平均频率的方案，这样可以获得适合本地的最佳订正方案。频率统计可以是基于空间上的(如面预报)或时间上的(如单站预报)或二者兼用(多数情况下被釆用的方法如本研究)。一般而言，降水偏差会随模式预报时效、降水阈值和具体天气过程的不同而不同, 所以降水订正工作最好要对不同时效的预报、不同的降雨量和不同的天气形势过程分別单独进行订正。在本研究中我们区分了前二者但没有专门区分天气过程，这是以后需要改善的方面。

2.2 具体步骤

本文选取2012年5月11日至8月31日 我国大部地区降水集中期期间每天AREM模式1(0~24 h)~2(24~48 h)d日降水(24 h累积量)预报结果，插值到全国2510个站，同时以这些站点的观测作为实况资料, 每天采用站点统计的方式计算降水频率和评分(以下订正工作都是基于站点而不是在模式格点上进行的)。对24和48 h的预报分别进行统计, 共统计了0.1、1、5、10、25、35、50、80、100、150 mm 10个阈值的频率分布。预报和实况降水频率的计算方法如下：

${{F}_{频j}}=\frac{\sum\limits_{i=1}^{i=20}{{{B}_{_{j}}}}}{\sum\limits_{i=1}^{i=20}{A}}$

(9)

式中，F_频为某个阈值降水的平均频率，B为某个阈值降水每天出现的总站次，j代表某个降水阈值，A为每天的总站次，i表示滑动平均窗口的天数。为了有足够的样本数而又大致考虑到近期相似的总天气形势，本文采取过去20 d滑动平均的方法计算降水的平均频率。

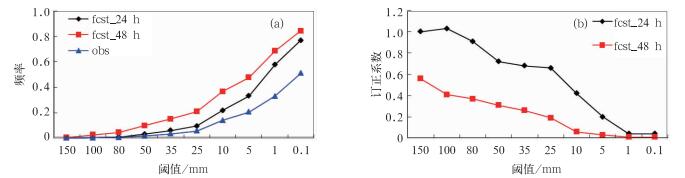
图 3a以2012年7月1日为例，计算得到前20 d 实况和模式预报降水的频率分布，如图所示，模式各阈值的降水预报频率均大于实况，表明预报与实况相比具有明显的湿偏差，且48 h降水预报的湿偏差更明显，这与上述AREM模式降水预报偏差特征基本一致。然后，根据计算得到的前期预报和实况在不同阈值上的频率分布，通过多项式插值的方法，得到不同阈值降水预报的订正系数，图 3b即为通过频率匹配(将模式降水预报频率调整到与实况相当)计算得到的7月1日当天模式24和48 h预报各阈值的订正系数，当实况频率小于预报频率，订正系数小于1(如图 3b所示24和48 h预报时段多数阈值的订正系数)，反之，则订正系数大于1(如图 3b所示fcst_24大于100 mm阈值的订正系数)。此外，小量级降水预报的频率具有较大正偏差，对应订正系数小于1且偏离1较大，故调整幅度大，消除小雨的空报，大量级降水实况和预报的频率比较接近，对应订正系数接近1，调整幅度小，并且对48 h降水预报的调整幅度大于24 h(这与2.3节模式的总体偏差特征也是一致)。

最后，根据以上计算得到的这组各阈值上的订正系数，采取内插方式就可以获得对任何降水量的订正系数, 用该订正系数乘以对应站点的原降水量就得到订正后的降水量，总之，订正系数调整预报雨量的大小，使得模式降水预报频率与实况相当。采用以上方法逐一订正2510个站点的预报结果，并逐日滚动。订正从6月1日开始，5月11—31日的资料用于初始时刻观测和预报降水频率的统计，得到6—8月每天订正后的降水预报。2.3节将基于这92 d 2510个站的平均订正结果进行分析。

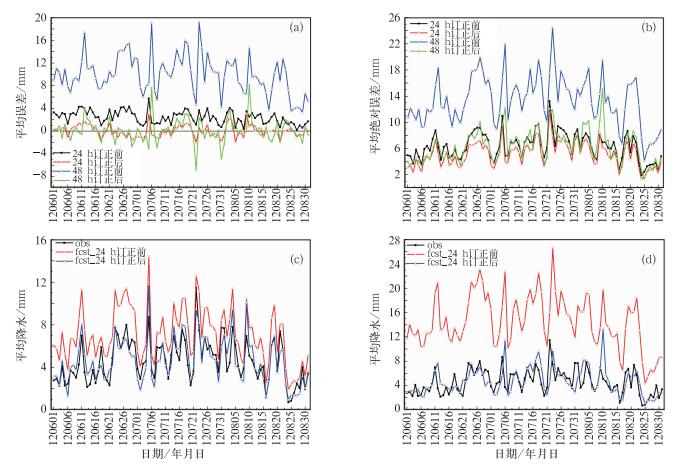
2.3 试验结果及分析 2.3.1 对降水强度预报的影响

图 4a和4b为订正前后24 h累积降水量预报的2012年6—8月逐日平均误差(即降水量的偏差, 式2)和绝对误差(式3)。从逐日平均误差的变化看(图 4a)，订正前两个预报时段的误差均为正值，反映出模式降水量存在系统性的湿偏差，订正后的平均误差曲线在0线附近上下波动，24 h预报的偏差波动范围在正负2 mm左右，48 h预报的偏差波动范围要稍大一些，降水预报的雨量系统误差基本得到矫正。此法对雨量偏差的显著订正作用不难理解，因为此法直接调整的对象就是雨量值本身(图 2a)。订正后预报的雨量绝对误差也得到明显改善(图 4b)，48 h预报改善更加明显(这是因为它原来的偏差较大的缘故)，订正后的24~48 h时段的平均绝对误差水平与订正前0~24 h时段相当。当偏差消除后其绝对误差也大大地减少，这表明AREM模式预报中降水强度的误差大部分可能是由偏差造成的(这对今后该模式的发展提供了非常有价值的信息)。

图 4c和4d给出了实况和预报平均日降水量的逐日演变。如图所示，模式预报的逐日平均降水变化趋势与实况比较接近，表明AREM模式能正确反映主要降水过程的变化，但模式预报的日平均降水均大于实况，24~48 h时段表现更为突出(图 4d)。经过订正，24和48 h日降水量的预报与实况基本接近。同时我们也看到，当实况出现较大降水过程时预报偏差和绝对误差也更加明显, 这说明降水量误差的大小与实况降水强度的大小有大致的正相关。

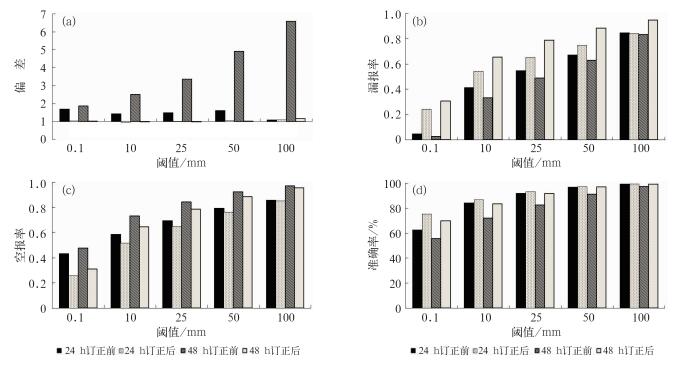
2.3.2 对降水范围(面积)预报的影响

图 5a为订正前后降水预报雨区范围大小的偏差BIAS(式1) 。订正前模式具有一致的湿偏差特征即预报雨区偏大，尤其是24~48 h时段; 订正后，偏差得到显著改善，各个量级的偏差均保持在1左右。同雨量偏差能被显著订正一样, 雨区面积偏差能被显著订正的原因也同本法的基本假定即“雨区面积的匹配”(图 2b和2c)有关。由于降水范围大小在订正前后改变了，降水的空报率(式4)和漏报率(式5)也会随之改变。一般说来，在预报雨区过大(湿偏差)情况下订正后会使降水范围缩小从而使空报率下降而漏报率上升；反之, 在预报雨区过小(干偏差)情况下订正后则会使降水范围扩大从而使空报率上升而漏报率下降。图 5b和5c分别为漏报率和空报率。如图所示，随着预报阈值的提高，模式降水预报的空、漏报率也增大; 对比图 5b和5c，订正前模式降水预报的空报率明显高于漏报率，尤其在小雨量级上，并且24~48 h时段的空报率普遍高于0~24 h时段。订正后，降水预报的空报率下降，漏报率却相应有所增加(这也是下文TS和ETS评分改善不明显的原因之一, 详细讨论见2.3.3)，但订正后的空、漏报率相当，两者比较均衡，结果更加合理。改进后各量级“晴雨”预报的准确率(式6a) 都有提高(图 5d)，其中小雨量级的预报准确率提高最为显著，这是因为大片虚报的小雨量降水区被订正消除了(见2.3.4个例分析);24~48 h 时段比0~24 h时段提高明显, 这是因为24~48 h时段的偏差较大。

2.3.3 对降水落区位置预报的影响

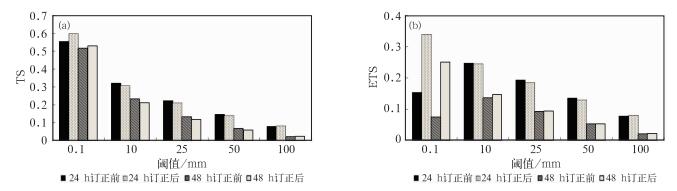
在此采用降水预报检验中经常应用的TS(式7)和ETS(式8)评分来描述降水落区位置预报的准确性(Du et al，1997)。图 6a和6b分别给出了TS、ETS评分的结果。从TS评分来看，在0~24 h和24~48 h两个预报时段，订正后小雨和大暴雨量级的评分都有改善，其中小雨量级的预报改善较明显，其他量级降水有弱的负订正效果。从ETS评分结果看，订正后对小雨量级的改善更加显著，其两个预报时段的ETS评分分别提高了122%和239%，大暴雨量级的评分也略有改善, 其他量级降水的ETS评分改进前后相差不大。改进主要表现在小雨量段和大雨量段的原因是两端降水的偏差都较大，其中小雨量降水段有大片虚报的面积(见2.3.4个例分析)，而大雨量降水段虽然面积本身范围也许并不大但雨量偏差较大(图 4)，所以对两端订正的效果要明显一些。逐日的TS和ETS评分表明(图略), 订正后对小雨量级评分均有提高，也就是说，订正使数值预报的“有雨或无雨”的定性降水预报的质量有了明显、稳定的改善(同图 5d结果一致)。

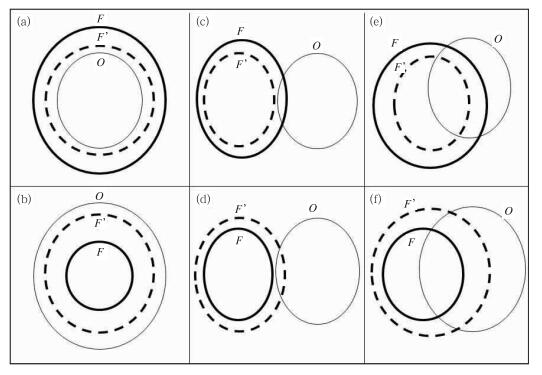
但总体说来，除了小雨量段以外，订正前后TS和ETS变化不大。为什么在雨量和雨区范围预报明显得到改善的情况下，而TS、ETS评分却没有改进呢? 根据以上讨论，该方法的基本原理是通过调节降水量来使得某一降水量级在预报中出现的频率(面积)与实况中的频率(面积)一致，所以在订正雨量和雨区范围偏差时有非常显著的效果，然而频率的统计是在一个区域內进行的而没有考虑具体的位置即并不区分具体格点或站点、也没有考虑任何雨区的形状或走向的误差，所以本方法没有能力也不能用来订正雨区的位置偏差。换句话说, 因为TS或ETS评分主要是衡量降水落区的准确性(当然, 一部分也同降水面积大小有关)，所以TS或ETS评分不适合用来检验本方法的优劣。一般来说，这一订正方法对TS、ETS评分影响不大，下面来具体分析此法如何影响这二种评分(图 7): (1) 当降水落区大致正确时，在湿偏差情况下(图 7a)订正后会使空报区缩小, 在干偏差情况下(图 7b)会使报对区域增大和漏报区缩小，这二种情形都会使TS和ETS评分得到改进；(2) 而在降水落区基本报错的情况下，订正后或使TS和ETS变得更差(在原湿偏差下会使仅有的微小报对区完全消失，当然空报区也会缩小一些，图 7c)或略有改善(在原干偏差情况下或许会增加报对区，但同时也伴随着空报率的增加，图 7d)；(3) 而在界于上述两者之间的情况下，订正前后的TS和ETS应该变化不大，这是因为订正后虽然报对区或有缩小(湿偏差时，图 7e)或增大(干偏差时，图 7f)，但由于空报率和漏报率这对孪生姐妹的作用总是互相抵消——在湿偏差情况下空报率减少而漏报率上升，反之在干偏差情况下空报率上升而漏报率减少, 所以从式(7)和(8)可以推得它们的净改变不大。要TS和ETS在订正前后有较明显的改变，订正前后降水面积的改变必须相当大如前面所看到的小雨量降水区。

2.3.4 个例分析

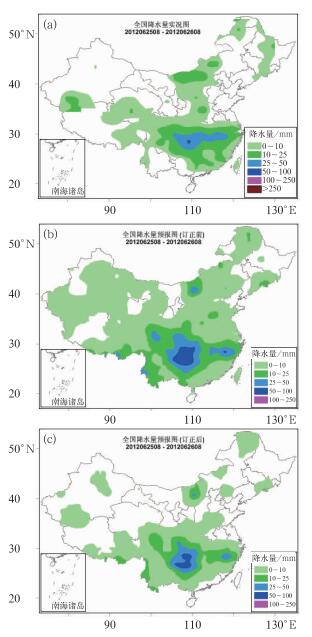
同上面讨论相一致，通过对批量降水过程订正前后具体预报结果的分析，使用该订正方法，选择位置预报较好的个例，通过订正能进一步改善其强度预报，因而订正效果较好；但对于主雨带和分布预报出现重大偏差的个例，使用该方法并不能改进雨区 位置的预报。图 8给出了一次降水过程24 h预报订正前后的具体结果，如图所示，订正前模式预报出了降水的总体分布特征，主雨带的位置，但小雨雨区明显偏大，强降水中心的范围也明显偏大，通过订正，小雨范围减小，雨区范围与实况比较接近，强降水中心的强度和范围也得到了订正，减小了强降水的空报。但从图中也可看出，尽管雨量大小和雨区范围的偏差得到了订正，但雨区的形状(走向)在订正前后变化不大。其ETS评分表明(略)，由于小雨和中雨区得到明显订正，其ETS评分也得到提高，尤其小雨量级提高明显(与图 7a情况类似)，但大雨和暴雨区在减小空报率的同时，其漏报率增加，故其ETS评分前后变化不大(与图 7e情况类似)。因此可见，采用频率或面积匹配方法，对系统性降水或大范围降水订正效果较好(降水落区预报较好)，而对于局地降水或小范围降水的订正效果较差(降水落区预报不理想)。

3 结论和讨论

本文重点介绍了降水频率或面积匹配方法的基本原理及其实现过程，并基于AREM模式降水预报产品检验该方法是否有效, 最后根据该方法的原理深入探讨所得结果的原因，并指出其优缺点和注意事项，以期为进行降水偏差订正的相关科研和业务工作提供借鉴。结果表明：

(1) 基于频率或面积匹配的降水偏差订正方法能有效订正降水预报雨量和雨区面积的系统性偏差。订正后，降水量和雨区面积的预报得到明显改善，其空、漏报率比较均衡且更加合理，因而各量级的预报准确率都有提高。

(2) 通过改变雨区范围的大小，订正后降水预报的TS和ETS的评分也有一定程度提高, 本试验中TS、ETS评分表明订正后小雨和大暴雨量级有所提高，特别是对小雨量降水段的改进尤其显著，消除了大片虚报的小雨量区, 也就是说，订正使数值预报的“有雨或无雨”的定性降水预报的质量明显得到了改善。

(3) 因为该方法类似于分段订正函数，总是将降水预报频率调整到与实况一致，偏差越大，调整的幅度越大，订正效果越明显。研究中48 h预报的降水量偏差大于24 h的预报，所以本方法对48 h的降水预报改进效果更加显著；较大的偏差出现在小量级降水和强降水上，该方法对降水预报的改进也主要表现在这两端。

(4) 在原理上, 本方法没有能力也不能用来订正雨区位置的偏差。在降水落区准确的情形下, 订正会使TS和ETS评分得到改进; 但如果在降水落区错报的情形下, TS和ETS在订正前后改变应该不大甚至变差。要TS和ETS在订正前后有较明显的改变，订正前后降水面积的改变必须相当大。这解释了为什么对降水落区预报较好的个例，通过订正能进一步改善其强度预报，订正效果较好；但对于降水落区预报出现重大偏差的个例, 使用该方法并不能改进预报结果。一般情况下，对系统性降水或大范围降水订正效果较好，而对于局地降水或小范围降水的订正效果较差。因此，对一些天气过程预报能力较强的模式如T639、欧洲细网格预报等，采用该方案，可以在保留原落区预报准确的前提下，进一步提高其量级预报的精度。而对于降水落区预报的改进，则需要靠模式自身预报能力的改善，如提高模式的同化能力以提高模式初始场精度，选取适当的模式物理过程或有针对性地改进模式物理过程等。

针对该方法不能有效改进降水落区预报偏差的局限，今后可以改进和尝试的方面包括: 第一，针对不同降水类型或天气形势分别进行订正(任宏利等，2005；Hammil et al, 2006；Greybush et al, 2008)。第二，虽然本文讨论的是面降水预报，但此方法也可用来订正单站的降水。这样就可不涉及降水落区问题，而只要“有或无”定性降水报对时，本方法就可用来有效地订正其降水的强度了。虽然这需要进一步的工作来证实，但在本文的平均降水量偏差订正分析中可以看出它的有效性(图 4)。第三，可以考虑同集合预报(杜钧，2002；杜钧等，2010) 相结合来估计降水落区的不确定性并尽量加以消除。第四，可以同物理或动力因子诊断方法(高守亭，2007)相结合来识别最佳的降水落区。第五，进一步研发专门用来改进落区预报的偏差订正方法, 这种方法一方面可同天气形势系统偏差相结合(Yuan et al, 2007)，另一方面可基于雨区形状和走向的系统性误差的统计信息(Du et al, 1997； 2000；Marsh et al，2012)。最后, 因为降水量和降水范围大小对水文的流域预报特别重要(James et al，2012)，而本方法对二者的订正效果又特别显著, 因而该方法在水文气象预报中会有广泛的应用前景。除降水偏差订正外, 该方法原理也可直接推广应用到其他类似预报量(如雾等的订正)。