随着我国社会经济的快速发展,高速公路的建设正在以前所未有的速度改变着人们的生产、生活环境,改变着经济发展格局。但是,我国高速公路面临的交通安全问题十分严峻。国内高速公路交通事故的严重性不能不引起我们的高度重视和思考。由于大雾天气导致能见度降低而引发多达近百辆汽车追尾相撞的特大交通事故;因为路面的低温、雪后湿滑结冰,车辆发生侧翻,车内乘客均被摔出车外,造成群死群伤的严重事故;每起重大交通事故都会给我国国民经济和人民生活带巨大的危害。因此,研究不利天气与高速公路交通事故的关系意义重大。开展高等级公路的气象灾害监测预警及服务系统的建设,将有助于提高公路交通气象服务能力,从而更好地发挥气象、公路交通在国民经济发展中的基础性作用,研究与交通运营管理相适应的气象灾害的预警、临近预报技术,探索交通气象服务新模式,已成为我国当前气象科研和服务中的一个新课题(Mario et al,2010;Maze et al,2006;Milton et al,2008;Qiu et al, 2008)。交通和气象专家们从高速公路的建设施工、安全管理方面,进行了气候变化、气象要素、极端天气过程在不同时段对公路交通的影响(罗慧等,2007;李建科,2008;潘娅英等,2006;王俊骅,2009;张青珍等,2007;吴彬贵等,2009;窦以文等,2011;丁德平等,2011),其成果正在高速公路的管理中试验和初步应用尝试。通过了解国内外相关的学术研究,应用G2京津塘高速公路万辆车流交通事故与综合气象参数(逐时平均气温、平均相对湿度、平均能见度、降水量等气象要素)相关性分析,建立未来24 h万辆车流交通事故的预报模式,以“交通气象安全指数‘的产品服务于高速公路,对于提高高速公路安全运营管理将具有科学的指导意义。
1 万辆车流的交通事故和气象观测资料的统计整理整理了2007年7月1日至2009年6月30日期间的交通事故和交通流量及气象观测资料(2年整),其中G2京津塘高速公路(北京、天津、河北3段全程142.69 km)各月逐时出现的交通事故总次数,连续样本数2 a×365 d·a-1×24 h·d-1=17520 h,资料完整;G2高速公路3个桩号的交通流量数据Vd01(k1+500)、Vd27(k55+660)、Vd24(k134+130)3个桩号分别距北京四环路东南角十八里店1.50、55.66和134.13 km,统计出与全程交通事故相同的连续样本数24月×24个/月=576个;统计出北京市观象台、廊坊市气象台、塘沽市气象台各月逐时4个气象要素:气温(单位:℃)、相对湿度(单位:%)、降水量(单位:mm)和能见度(单位:km)。各气象要素的连续样本数均为2 a×365 d·a-1×24 h·d-1=17520 h,资料完整。能见度的数值是选择距离3个气象台站最近的高速公路上的大羊坊北桥、廊坊、塘沽西道面监测站的监测值。在G2京津塘高速公路有建路时匹配的道面监测站,由于仪器从未检定,缺测与误差偏大,故此选择气象部门的3个道面监测站。
1.1 万辆车流的交通事故的定义在高速公路上行驶的机动车辆,因为路况、天气、车辆机械、驾驶员身体等种种因素出现的轻微事故、一般事故、重大事故、特大事故统称为交通事故。通过设置在高速公路上桩号,读取断面交通量双向日报统计数据(大车流量加小车流量)称为交通流量。交通事故/交通流量×104=一万辆车流量所发生的交通事故起数(因为逐时平均交通流量最大可超过万辆,而逐时交通事故最多十几起,二者之商数字很小,故采用乘以10000来计算),简称为万辆车流的交通事故(单位为:起/万辆)。
1.2 万辆车流的交通事故和气象要素的统计方法为了探讨万辆车流的交通事故的日变化特点与气象要素日变化之间的关系,按月份统计2年的逐时万辆车流的交通事故和气象要素的平均数值, 见如式(1)[式(1) 和式(2) 适用于12个月]。
| $ \overline {{Y_i}} = \frac{1}{n}\sum\limits_{j = 1}^n {{y_{ij}}} $ | (1) |
式中,
| $ \overline {{X_{ip}}} = \frac{1}{k} \cdot \frac{1}{n}\sum\limits_{k = 1}^m {\sum\limits_{j = 1}^n {{x_{ipjk}}} } $ | (2) |
式中,
由式(1) 统计出G2高速公路全程的各月的逐时平均万辆车流的交通事故数值;由式(2) 统计出北京市观象台、廊坊市气象台、塘沽市气象台的各月各气象要素的各月逐时平均数值,即:统计3个气象站的气象要素监测数据的平均数值代表G2高速公路全程平均气象要素值。
2 万辆车流交通事故的分析随着季节的昼夜长短和气候的差异,各月万辆车流交通事故的日变化也存在较明显的区别。由此,逐月分析万辆车流交通事故的日变化趋势,是探讨气象要素对万辆车流交通事故的关系和预报未来24 h逐时交通气象安全指数的基础。
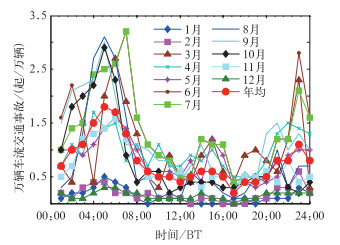
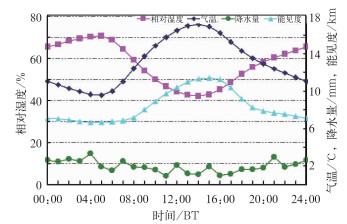
2.1 万辆车流交通事故的日变化分布如果仅仅分析交通事故与气象要素的关系,则平均交通事故的高峰值出现在07时,此时正是交通运营的高峰时段,自然容易出现交通事故,必然是交通事故特点。为了避开交通高峰的嫌疑,重新收集对应的气象观测站附近的3个桩号的交通流量资料,并用交通事故除以交通流量,得到一万辆交通流量的交通事故。图 1为由式(1) 计算出G2高速公路的各月平均万辆车流交通事故分布。可以得到各月平均万辆车流交通事故在一日内的变化趋势为双峰型,其中,3、6、7月的双峰型尤为突出。平均每一万辆交通流量的交通事故主高峰出现在05时,次高峰出现在23时。05时前后通常是一天中气温最低谷、降水量概率较大、相对湿度最大、能见度较差的时段(图 2);而日落后到23时,气温迅速下降、能见度递减较快,相对湿度开始递增、降水概率略次于05时。因此这种变化反映了万辆车流交通事故量与气象要素的变化的关联性。另外,14—15时还存在一次万辆车流交通事故的小波动,该波动与日最高气温时段会影响人的交感神经进入疲惫状态有关(张书余等,2010)。综上,不难理解气象要素日变化对万辆车流交通事故的影响了。
|
图 1 G2高速公路各月逐时万辆车流交通事故日变化曲线图 Fig. 1 Diurnal variation curves of traffic accident by per million traffic flow on G2 Highway in different months |
|
图 2 G2高速公路2年3个气象监测站气象要素日变化曲线图 Fig. 2 Diurnal variation curves of meteorological elements observed by the three monitoring stations on G2 Highway |
应用式(1) 和式(2) 的统计结果,分别将各月的逐时万辆车流的交通事故与同步的各气象要素进行相关分析,发现诸气象要素与万辆车流的交通事故均存在着比较密切的关系,其中尤以气温、水平能见度、降水量、相对湿度与万辆车流的交通事故的关系最为密切。其中相对湿度和降水量与万辆车流的交通事故呈正相关,相对湿度和降水量增大时,会增加高速公路的道面湿滑度,路面摩擦系数减小;气温和能见度与万辆车流的交通事故呈负相关。例如,万辆车流的交通事故的高峰出现在早晨前后,而此时恰好是日气温最低、能见度较小、相对湿度最大和降水概率偏大的时段。气温、水平能见度、降水量、相对湿度的变化除了直接影响高速公路路况外,还影响人的正常生理状况(人体的最佳舒适状况是对应于季、月、日的平均气候环境的,当气象要素的变化超出平均气候条件,将影响人的正常活动;如气温降低,影响血液的正常循环;能见度减小,影响人的正常视力等)。为了归纳诸气象要素共同对万辆车流的交通事故影响程度,通过反复试验组合,建立综合气象要素参数关系式(简称综合气象参数),达到万辆车流的交通事故随综合气象参数日变化增大而增多的效果。参考经验公式(李庆祥等,2006;陶澍,1994),选择气温、水平能见度、降水量和相对湿度不同的组合方式,使其与万辆车流的交通事故关系最为密切,分月组合气温、水平能见度、降水量和相对湿度的气象综合参数如下式(3)~(5) 所示。
| $ C{I_{3 - 5{\rm{月}}i}} = \frac{{{H_i}\left({0.1 + {R_i}} \right)}}{{{V_i}\left({10 + {T_i}} \right)}} $ | (3) |
| $ C{I_{6 - 11{\rm{月}}i}} = \frac{{{H_i}}}{{{V_i}\left({10 + {T_i}} \right)}} $ | (4) |
| $ C{I_{12 - 2{\rm{月}}i}} = \frac{{{H_i}\left({0.1 + {R_i}} \right)}}{{{V_i}\left({20 + {T_i}} \right)}} $ | (5) |
式中,CI为气象综合参数(后文简称CI),H为某时平均相对湿度,R为某时平均降水量(降水量加0.1,为了解决某时无降水为0的问题),Vi为某时平均能见度,T为某时的气温(气温加10或20,为解决某些时刻气温≤0℃的问题),i与式(1) 含义相同,由此,CI的日变化趋势与万辆车流的交通事故的日变化趋势一致,即万辆车流的交通事故随CI增大而增多,简化了万辆车流交通事故与逐气象要素的相关分析过程,为直观地研究万辆车流的交通事故日变化与同步气象要素日变化的关系开阔了思路。
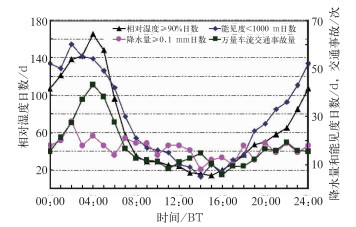
2.3 低能见度和雨雪日数与万辆车流交通事故的关系统计直接影响G2高速公路交通事故的天气日数,分析2年中3个气象站及道面气象监测站的平均低能见度日数(V<1000 m)、降雨雪日数(R≥0.1 mm)、大相对湿度日数(H≥90%)和万辆车流交通事故次数的关系(图 3)。在04—06时,低能见度和大相对湿度日数明显偏多,雨雪日数相对偏多,恰值万辆车流交通事故次数的高峰时段;在09—19时3种气象条件的日数明显偏少,万辆车流交通事故次数则处在低谷值波动。出现浓雾和雨雪天气时,能见度和路面摩擦系数减小、相对湿度增大、气温下降。可见,低能见度和雨雪天气是引发高速公路交通事故重要原因之一。
|
图 3 2年低能见度和雨雪日数与万辆车流交通事故的日变化曲线图 Fig. 3 Diurnal variation curves of traffic accident per millions traffic flow, low visibility and rain/snow days |
应用统计学的方法分析了各月的万辆车流的交通事故与CI值的日变化的相关程度(陶澍,1994),均通过了F检验(Fα=0.01=4.26,rα=0.01=0.496),见表 1。为了与独立样本分析比较(所获交通事故仅到2010年2月),选择冬夏两季的研究对象与CI值相关系数最大的8月和相关系数最小的12月为例,进行万辆车流的交通事故与同步CI值的日变化的相关的分析。
|
|
表 1 各月份的平均万辆车流的交通事故与CI值相关的显著性检验参数一览表 Table 1 Significant test parameters between traffic accident and CI values in different months |
为避免各月多处相近似的分析描述,选择表 1中相关系数最大的8月(夏季第三个月)和相隔6个月的冬季(第三个月)的2月为分析研究对象。
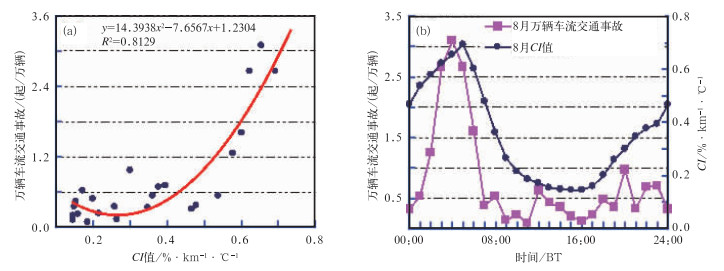
由表 1可见,8月的平均万辆车流的交通事故与同步CI值的日变化的相关程度高达0.9016,其相关程度和曲线的日变化趋势见图 4。
|
图 4 8月万辆车流的交通事故与同步CI值散点图(a)及日变化曲线趋势(b)[单位:%/(km-1·℃-1)] Fig. 4 Diurnal variations curves of traffic accident and CI values during August [unit:%/(km-1·℃-1)] |
图 4反映了8月逐时平均万辆车流的交通事故与同步CI值呈抛物线相关和日变化趋势的一致性。从图 4a看到,万辆车流的交通事故随CI值呈二次方程曲线趋势增长;其相关系数居各月之首。在图 4b中,01—05时,万辆车流的交通事故迅速增多(增多幅度0.7675起/万辆·小时);在05—17时期间,CI值以乘幂指数迅速变小。总之,CI值与万辆车流的交通事故的日变化趋势是吻合的,出现高峰与低谷的时间前后相差1 h:万辆车流的交通事故偏前CI值1 h,是因为夏季日出早,交通运营时间提前所致。这种现象说明了CI值的日变化对高速公路驾驶员安全行车的影响是明显的。
图 5描述了2月平均逐时平均万辆车流的交通事故与同步CI值呈指数相关关系,相关系数为0.8196。图 5b比图 4b的曲线的变化趋势更逼近一致性,但是,2月万辆车流交通事故曲线的主高峰值出现在23时,次高峰出现在05时。这事实不仅证实了气温、相对湿度和能见度的日变化与高速公路交通安全有关之外,而且,冬季夜间的降雪天气对高速公路安全行车也显得尤为重要。当然与春节假日夜间车流量增多也是密不可分的。
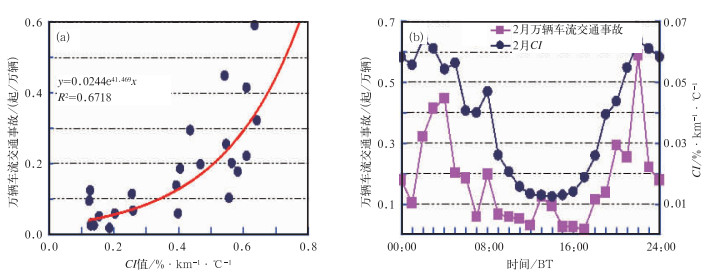
|
图 5 2月万辆车流的交通事故与同步CI值散点图(a)及其日变化曲线趋势(b) [单位: %/(km-1·℃-1)] Fig. 5 Diurnal variation curves of traffic accident and CI values during February [unit: %/(km-1·℃-1)] |
为了业务应用中方便司机记忆,采用经验概率密度分级方法,将万辆车流的交通事故的气象风险划分为4个等级,即:交通气象安全指数为4,气象风险大(万辆车流的交通事故的概率密度占5%);交通气象安全指数为3,气象风险较大(万辆车流的交通事故的概率密度占20%);交通气象安全指数为2,气象风险较小(万辆车流的交通事故的概率密度占45%);交通气象安全指数为1,气象风险很小(万辆车流的交通事故的概率密度为30%)。按照万辆车流交通事故的概率区间划分出交通气象安全指数的等级标准(丁德平等,2012)(表 2)。表 2中表明,交通气象安全指数的等级越高,万辆车流的交通事故的次数越多,气象风险越大;其中,6月、8—10月交通气象安全指数等级为4时,万辆车流的交通事故较高,均在2.7起/万辆以上。
|
|
表 2 万辆车流交通事故的概率区间划分交通气象安全指数的等级标准 Table 2 The grade standards of traffic security indexes by using probability intervals to divide the traffic accidents |
选择G2京津塘高速公路3个气象监测站2009年8月和2010年2月逐日逐时的气温、相对湿度、能见度和降水量的独立样本计算出综合气象参数(CI值),应用表 1中的2和8月的万辆车流的交通事故与气象综合参数(CI值)的关系式得到万辆车流的交通的预报量,并按照表 2中的阈值标准得到综合参数的预报试验结果(表 3)。表 3中“综合参数的预报试验”表明,8月的逐时平均交通气象安全指数等级预报准确率高于2月,2月交通气象安全指数等级预报与实况完全一致的准确率仅为16.7%,8月为54.2%;2月交通气象安全指数等级预报准确率较低的原因与春节长假有一定的关系,即超出了纯气象综合参数的影响范畴。如果把预报准确率评定标准放宽一个等级,8月预报准确率为95.8%,2月预报准确率达66.7%,该结果为开展交通气象服务还是具有较好参考价值的。
|
|
表 3 万辆车流交通事故预报模式的独立样本试验一览表 Table 3 Independent sample test of forecast model of traffic accident |
应用北京城市气象研究所的WRF-RUC数值预报产品,读取各网格点上11时起报的未来24 h的逐时的气温、相对湿度、水平能见度和降水量计算出综合气象参数(CI值),同理可以得到RUC产品的预报试验结果(气象风险等级与交通气象安全指数等级相同)。从表 3中的“WRF-RUC产品的预报试验”结果看,8月的交通气象安全指数预报的准确率与综合气象参数实况的预报试验结果相同,但是,当某日遇有降水影响能见度的时次,气象综合参数均在1左右,相应的交通气象安全指数预报等级为4或3,表明低能见度、相对湿度大、气温偏低将严重影响高速公路汽车行使的安全。2月的交通气象安全指数预报的准确率与综合气象参数实况的预报试验结果相近,不再赘述。由此,应用WRF-RUC数值预报产品二次开发的交通气象安全指数预报产品,可以推广到交通沿线的气象服务,其效果将优于《北京奥运赛期的交通路段精细化气象预报服务》的产品(丁德平等,2012;张德山等,2002;2009)。
5 结论通过G2京津塘高速公路全程逐月逐时的平均万辆车流交通事故与沿线3个代表气象站的综合气象参数的相关分析,得出各月非线性相关关系式,应用经验概率密度分级方法,将万辆车流的交通事故的气象风险划分为4个等级,即交通气象安全指数,为开展高速公路的气象服务增加服务产品。限于仅能得到G2京津塘高速公路全程各时次的月总交通事故量(无法获得逐日的全程交通事故量)的条件,未能进行逐日逐时的万辆车流交通事故与综合气象参数的相关分析。在此,只好试图应用上述的分析成果,借助2009年8月和2012年2月的WRF-RUC数值预报产品输出的历史气象要素预报样本,计算逐日的综合气象参数,代入各月万辆车流交通事故的非线性相关关系式,得出逐日的万辆车流交通事故量,此结果转换为交通气象指数,直接为高速公路管理部门和大众传媒媒体开展服务。WRF-RUC数值预报产品的独立样本试验结果的月平均准确率与同期天气实况试验结果吻合。就是说,应用WRF-RUC数值预报产品开展高速公路交通气象安全指数预报服务是可行的,在华北地区高速公路气象服务中具有推广价值。
致谢:感谢交通运输部公路科学研究院的李斌,刘文峰和张利在交通安全方面提出的建设性意见。
丁德平, 李迅, 张德山, 2012. G2京津塘高速公路万辆车流的交通事故灾害与气象综合指数的关系[J]. 灾害学, (3): 107-110. |
丁德平, 尹志聪, 李迅, 2011. 京津塘高速交通事故与气象条件之间的关系[J]. 公路交通科技, 28(增刊): 115-119. |
窦以文, 丁德平, 李迅, 2011. G2京津塘高速公路交通事故与降水量相关性分析[J]. 交通运输系统工程与信息杂志, 11(6): 182-187. |
李建科. 2008. 陕西省公路交通气象条件分析及预报系统研制. 兰州: 兰州大学. http://cdmd.cnki.com.cn/Article/CDMD-10730-2008163202.htm
|
李庆祥, 朱燕君, 熊安元, 2006. 北京等6城市奥运期间不利天气条件的概率统计[J]. 应用气象学报, 17(增刊): 42-47. |
罗慧, 李良序, 胡胜, 等, 2007. 公路交通事故与气象条件关系及其气象预警模型[J]. 应用气象学报, 18(3): 350-357. |
潘娅英, 陈武, 2006. 引发公路交通事故的气象条件分析[J]. 气象科技, 34(6): 778-782. |
陶澍. 1994. 应用数理统计方法. 北京: 中国环境科学出版社: 160-161, 292-365.
|
王俊骅, 2009. 新疆高等级公路交通安全气象影响分析与评价[J]. 自然灾害学报, 18(6): 57-63. |
吴彬贵, 解以扬, 吴丹朱, 等, 2009. 京津塘高速公路秋冬季低能见度及应对措施[J]. 自然灾害学报, 18(4): 12-17. |
张德山, 丁德平, 穆启占, 等, 2009. 北京奥运赛期的交通路段精细化气象预报服务[J]. 应用气象学报, 20(3): 380-384. DOI:10.11898/1001-7313.20090316 |
张德山, 魏建明, 陈廷良, 2002. 首都机场高速公路能见度预报方法[J]. 气象科技, 31(6): 358-361. |
张青珍, 王慧芳, 张明捷, 等, 2007. 濮阳市公路交通事故气象条件分析[J]. 气象与环境科学, 30(B09): 78-80. |
张书余, 王宝鉴, 谢静芳, 等, 2010. 吉林省心脑血管疾病与气象条件关系分析和预报研究[J]. 气象, 36(9): 106-110. DOI:10.7519/j.issn.1000-0526.2010.09.017 |
Mario C, Elke M, Geert W, 2010. Assessing the impact of weather on traffic intensity[J]. Wea Climate Soc, 2(1): 60-68. DOI:10.1175/2009WCAS1014.1 |
Maze T H, Agarwai M, Burchett G, 2006. Whether weather matters to traffic demand, traffic safety, and traffic operations and flow[J]. Transportation Research Record: Journal of the Transportation Research Board, 1948(1): 170-176. |
Milton J C, Shankar V N, Mannering F L, 2008. Highway accident severities and the mixed logit model: An exploratory empirical analysis[J]. Accident Analysis & Prevention, 40(1): 260-266. |
Qiu L, Nixon W, 2008. Effects of Adverse Weather on Traffic Crashes: Systematic Review and Meta-Analysis[J]. Transportation Research Record: Journal of the Transportation Research Board, 2055: 139-146. DOI:10.3141/2055-16 |
 2014, Vol. 40
2014, Vol. 40 