引言

随着数值预报技术的水平日益提高，数值预报的环流形势预报质量已超过了预报员的预报水平，但要素预报的水平则相对较低(薛纪善, 2007)；从目前情况来看，由于客观条件的限制，数值预报模式本身要在要素预报上面有大幅的提高是不可能的。这就需要通过数值预报产品解释应用技术，来综合有用的信息，特别是数值预报模式环流形势预报的优势信息，得到比较好的客观气象要素预报。

以数值预报产品释用技术和预报员经验为依托，发展精细化气象要素短期预报业务，是现代天气预报业务的一个重要发展方向(端义宏, 2010；Kristine et al，2007)。改进基于稠密气象观测资料和高分辨率数值模式产品的气象要素预报释用技术，发展模式释用与交互订正相结合的站点、格点两种方式的精细化气象要素预报系统，是提高气象要素预报准确率的有效手段(端义宏等，2012；Ronald et al，2010)。根据中国气象局未来发展规划，要建立全国5 km格点和乡镇及其他服务地点的气象要素预报业务，提高温度、风、相对湿度等气象要素的预报准确率；提高预报员对各类灾害性天气识别和分析能力，发挥预报员对数值预报产品的释用和分析订正作用，做好灾害性天气种类、强度和落区预报。因此，进行数值预报产品释用技术的研究和应用是现代天气预报业务中极其重要的工作。

随着数值预报的发展，许多数值预报释用方法和技术得到了发展和应用。传统的数值预报释用方法为MOS方法和PP法，后来又发展了KALMAN滤波方法和神经网络等方法。马清等(2008)利用类似KALMAN滤波的自适应误差订正法对2 m温度预报进行订正，订正后温度预报误差明显减小。李莉等(2011)进一步利用自适应误差订正法对T213全球集合预报系统的系统性误差进行一阶偏差订正，取得了较好的订正效果。漆梁波等(2007)提出了最优化集成释用方法，对上海区域模式预报结果进行客观订正，要素预报准确率也有提高。王敏等(2012)采用非齐次高斯回归技术对2 m温度预报结果开展了一阶偏差和二阶离散度的校准研究，校准后的2 m温度预报评分有一定提高。但是随着数值预报模式发展和更替速度的加快，这种以多样本统计为基础的释用方法很难维持稳定。符娇兰(2012)对T639、ECMWF和日本模式中期预报性能进行了检验，结果表明，ECMWF模式预报效果最好。

新疆具有独特的天气气候特点和复杂的地形和下垫面特征(潘新民等，2012)。数值预报要素预报在新疆地区往往比其他地区评分要低，因此，在新疆进行精细化气象要素预报工作对数值预报产品的释用技术提出了更高的要求。新疆气象局现有的数值预报产品主要有，我国T639、T213和区域GRAPES模式产品，ECMWF中期数值预报产品和日本、德国的降水预报等。新疆气象台自己业务运行区域GRAPES模式，准业务运行WRF和MM5模式等。如何运用好这些模式预报产品，特别是用好我国自己研发的区域GRAPES业务产品，提高新疆地区精细化天气预报准确率，是当前新疆气象预报业务一项极端重要而又非常有意义的工作。

由于客观条件的限制，新疆过去的数值预报产品资料保存的不多，且不连续，很多基于统计方法的释用技术在新疆不能应用。根据新疆地区现有的区域业务数值预报模式的特征，本文首次提出了一种新的基于模式预报倾向的精细化预报方法，进行数值预报产品释用技术的研究和应用，用以提高新疆地区的精细化气象要素短期预报业务水平。该方法充分利用模式温度预报的倾向变化和新疆实际温度观测资料，进行温度预报释用方法的研究和应用。该方法不会受到历史资料短缺的限制，也不会由于模式的更新而改变释用方案，而会随着模式预报准确率的提高而提高要素预报水平；是一种全新的数值预报释用方法。

1 数值产品误差分析

传统上，用数值预报产品做气象台站的温度、风等气象要素的精细化预报，基本都是将数值模式输出的地面和等压面上的网格点数值产品插值到台站上做要素的预报。后来，有些气象工作者在此基础上，根据气象台站的海拔高度进行气象要素场的订正，如对温度进行订正(段旭等，2011)；也有人利用MOS方法进行数值预报产品释用的研究(林纾等，2010)，都取得了一定的效果。

但以上这些方法都存在着以下几种误差：(1) 模式初值误差；由于模式初值需要进行一定的同化和插值处理，模式要素的初值与台站实际观测值不会完全一致，必然会产生误差。(2) 数值模式地形与台站实际地形误差而导致的气象要素误差；数值模式的地形高度与气象台站的实际地形一般都不是完全一致的，因此需要根据模式地形与台站实际地形的差值对气象要素进行经验性订正。(3) 模式垂直坐标转换误差；数值模式的垂直坐标一般都是高度地形追随坐标或σ坐标，然后插值到等压面上输出，这必然产生误差。(4) 数值产品的插值误差；模式输出的网格点数值产品插值到各气象站点也必然产生误差。(5) 不同的模式背景场误差。

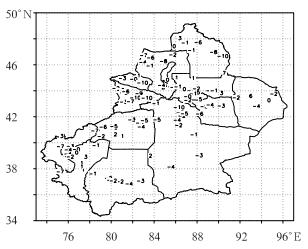
图 1给出了2012年3月20日08时(北京时)2 m温度的GRAPES模式初始场与观测场的差值，即模式在积分初始时刻的2 m温度插值到台站所在的站点，再与台站的实际观测温度相减得到的。从图中可以看到，进入模式的2 m温度初始场与观测场存在较明显的误差，总体来说，模式初始场温度低于观测场温度，其中新疆伊犁河谷到沿天山地区，模式初始值2 m温度明显低于观测场，最大可相差9~10℃，吐鲁番盆地、准格尔盆地和塔里木盆地的部分沙漠地区，初始值一般高于观测值，最大可高5~6℃。根据国家气象中心业务检验结果(王雨等，2013)，T639模式也存在这种明显的初值误差，据2012年全年的检验结果，T639模式在新疆南部存在-6~-3℃的负偏差，北疆存在2~3℃的正偏差，在青藏高原东部存在-17~-10℃的负偏差；ECMWF模式初始值2 m温度的偏差要小一些。这些误差的存在一方面说明需要对同化系统特别是对地面资料的同化进行更深入的研究和改进，以降低地面资料的模式初值误差；另一方面，由于新疆地形复杂，观测资料稀少，也使得初始场的改进存在非常大的困难。由于模式地形是从一个高分辨率的地形高度场中插值得到的，数值模式地形与台站实际地形必然存在误差，进而导致气象要素误差的存在，特别是温度要素预报存在误差，进行地形订正是需要的(佟华等，2006)；大部分订正方法一般是根据经验，地形高度每升高100 m温度下降0.6℃，这种方法在遇到逆温层时是存在明显错误的。其他几种误差也是明显存在的，这里不再详细分析论述。

本文提出的新的数值预报释用方法与前面提到的传统站点插值计算各气象要素相比，具有如下优点：(1) 新方案将预报倾向即要素的变化率累加到站点的初始值中，没有进行垂直坐标的变换插值运算，因而可避免前面分析的模式垂直坐标转换误差[即误差(3)]的产生；(2) 该方法充分利用了站点的观测信息，因而减少了模式初值误差[即误差(1)]；(3) 预报倾向与要素值本身相比是一个小量，将这个小量插值到站点，也减弱或减少了要素值本身(这个为大量)插值到站点而引起的误差[即误差(4)]。

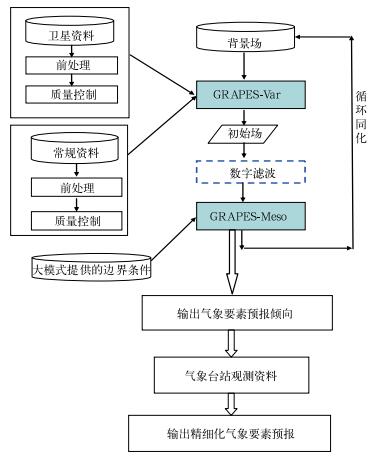
2 基于模式预报倾向的精细化预报系统设计

图 2为基于GRAPES模式预报倾向的精细化气象要素预报系统流程图。由图 2可知，基于模式预报倾向的精细化预报系统首先收集各种观测和大模式资料，进行同化分析，然后运行GRAPES-Meso模式，得到各预报时间的气象要素的预报倾向值，与气象台站观测数据进行合成分析，最终得到气象要素的预报值，即基于GRAPES模式预报倾向的精细化气象要素预报值。简单说，该预报系统主要由四个分系统组成：资料收集系统、GRAPES同化系统、GRAPES-Meso预报系统和精细化气象要素合成系统。其中精细化气象要素合成系统是通过气象要素的预报倾向值与气象台站的观测进行合成分析得到的，是一种新的数值预报产品释用方法。

3 数值预报倾向订正设计与结果分析 3.1 数值预报倾向订正设计

数值预报模式一般由动力框架和物理过程两部分组成，因此对要素预报的影响主要由这两部分组成，物理过程主要包括以下过程，辐射过程、对流过程、陆面过程和云微物理过程，还有一些其他过程，如地形重力波拖曳等影响相对较小的过程；需要说明的是，陆面过程包括边界层过程、陆面过程和表面层过程，这里统称为陆面过程；

设某要素为T，预报时间为t，则其倾向为ΔT/Δt，在Δt时间内，要素T的增量为ΔT，由数值模式结构分析可以得到，

$ \Delta T = \Delta {T_{{\rm{dyn}}}} + \Delta {T_{{\rm{rad}}}} + \Delta {T_{{\rm{conv}}}} + \Delta {T_{{\rm{mp}}}} + \Delta {T_{{\rm{iand}}}} + \Delta {T_{{\rm{oth}}}} $

(1)

式中, 右边6项分别为由于模式动力框架、模式辐射过程、对流过程、云微物理过程、陆面过程和其他物理过程引起的T变化量。

设经过倾向订正的要素为T₁，则有

$ {T_1} = {T_{{\rm{obs}}}} + \Delta T $

(2)

式中，T_obs为气象台站要素T的观测值。

2 m温度订正方案设计：本研究只对2 m温度进行订正，所以以上公式中的要素T为2 m温度。考虑到数值模式一开始积分要有1 h左右的SPIN-UP过程，并且模式预报60 h时长也大概需要1 h的计算机计算时间，因此本文开始订正时间是模式积分1 h后的预报倾向。其具体算法是，首先求出温度T在2 m高度的预报倾向累加之和，即模式动力框架、模式辐射过程、对流过程、云微物理过程、陆面过程和其他物理过程引起的温度倾向值之和，然后减去模式在积分1 h时刻的温度倾向值之和，则得到相对于模式积分1 h后的温度倾向值之和，该数值乘上模式积分1 h后的相对积分时间得到2 m温度的增量值，将这个增量值与积分1 h时刻的观测值相加，就得到经过订正后的2 m温度值。

由以上计算过程可以看出，在模式积分1 h时刻，温度倾向订正为0，即订正的温度值与实际观测值是一致的，而在模式积分的开始时刻至积分1 h时段内，2 m温度没有经过订正，即与原来模式预报值是一致的。

需要说明的是，现有的中尺度数值预报模式已经能很好地描述大气温度变化曲线，这种方法就是建立在模式大气的演变趋势与实际大气的基本一致的前提下研究出来的。随着数值预报的发展，模式预报准确率会不断提高，则该方法会越来越准确的预报2 m温度变化。该方法与温度地形订正法比较，具有明显优点，地形订正法遇到逆温层结时明显不适合，且会由于模式的更新或改变而需重新进行统计和经验订正，所以不够稳定；过去在新疆也曾经进行过温度地形订正，由于新疆冬季经常存在逆温层结，所以效果不好而取消。本文方法与其他MOS法比较也相对具有一定的优势，这种方法不需要较长的时间序列样本进行统计分析，不会由于模式的变化而重新进行统计分析。本方法与释用方法中的完全预报法(PP法)较相似，但本方法充分利用了台站观测资料，所以，也具有一定的优势。

为了检验基于GRAPES模式预报倾向的精细化气象要素预报系统的预报效果，对2012年3月20日的天气过程进行了模拟。模式初始场取美国FNL数据资料，初始积分时间是2012年3月20日08时(北京时)，时间步长取为90 s，共积分60 h；水平格距取0.15°，垂直方向为不等距的31层，模式层顶高度为35000 m。物理过程参数化方案采用如下选择：wms6微物理过程方案，RRTM长波和Goddard短波辐射方案，M-O近似的近地面层方案，热辐散(thermal diffusion)陆面过程方案，MRF边界层方案以及Betts-Miller-Janjic对流参数化方案。

气象要素预报倾向订正设计：利用2012年3月20日09时(北京时)的观测资料进行订正，即将GRAPES模式输出的2 m温度倾向叠加到观测值中，得到新的气象要素预报值，试验简写为：EXPREV。

3.2 EXPREV数值试验结果分析

由于新疆观测站点相对较稀少，因此新疆整个区域温度预报与观测相比可信度相对较差，所以本文只对比了站点的温度。

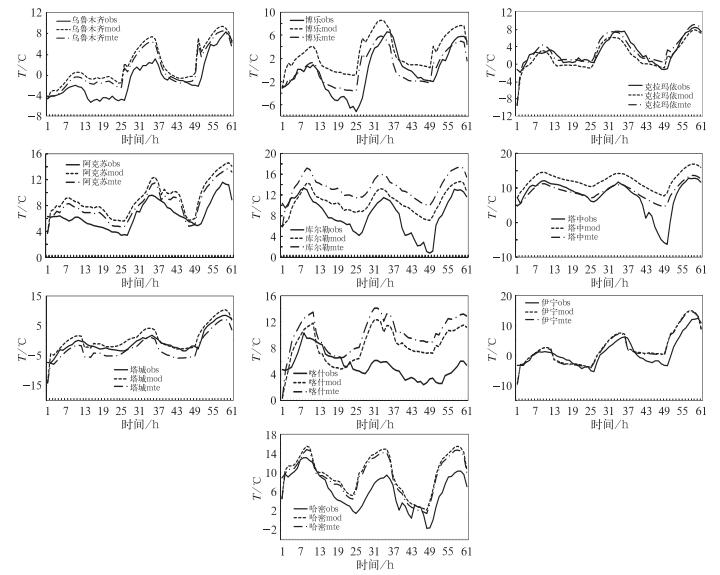
首先选取了乌鲁木齐、博乐、克拉玛依、阿克苏、库尔勒、塔中、塔城、喀什、伊宁和哈密等9个站点，制作了2 m温度预报与观测时间变化图(图 3)。黑色线为实际观测值，短虚线为模式直接预报值，长虚线为经过预报倾向订正后预报值。由图可见，GRAPES模式基本上都模拟出了2 m温度的每日变化趋势即温度日变化，但对温度变化的极值还存在较明显误差，除克拉玛依和塔城外，主要表现为，与观测相比，预报的温度极小值和极大值都偏高；再比较经过订正(长虚线)和模式直接输出的温度(短虚线)变化可以看出，经过预报倾向订正后，乌鲁木齐、博乐、阿克苏、塔中4个站温度预报更接近观测值，伊宁和哈密两个站略好于模式直接输出，即以上6个站的温度订正具有正效果；克拉玛依、塔城两个站模式直接输出与经过订正后的温度预报值各有优劣，预报效果基本相当；而喀什、库尔勒模式直接预报值要优于经过倾向订正后的温度值，即这两个站温度订正具有一定的负效果。

分析喀什和库尔勒这两个站产生负效果的原因，可能是，原模式积分1 h后的温度预报值小于观测值2~3℃左右，而模式积分6 h以后，预报的温度比实际观测温度高；经过观测订正后，必然使订正预报的温度升高，则最终结果使订正后温度整体高于观测值和原来模式的预报值，使得订正结果为负效果。其他站模式积分1 h后的预报温度一般高于或接近观测值，而后期的温度预报整体高于观测值，则经过观测订正后，使得订正的预报温度整体下降，从而更接近观测值或与观测值相当。

以上分析只是利用了一个时次观测数据进行的温度订正，已经取得了预报正效果，如果利用更多时次的观测资料和更多的数学技巧进行温度订正，则有望可以使订正的温度更加接近观测。

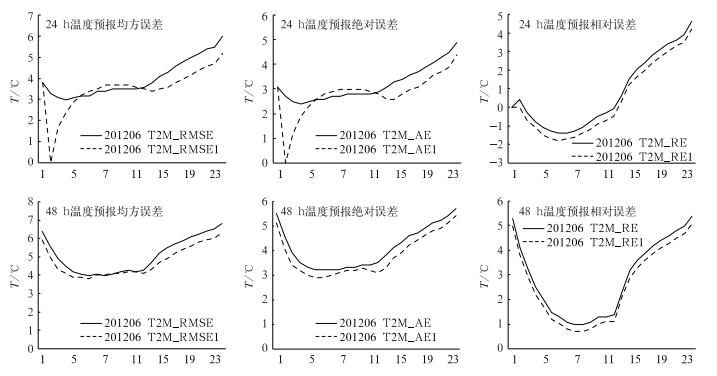
4 精细化气象要素预报系统的检验

为进一步检验和验证这种新的数值预报释用方法，本文给出了一个月的检验分析结果。图 4为2012年6月全新疆各台站08时(北京时)24和48 h 2 m温度预报图，实线为原来模式预报，虚线为修改后的预报，检验变量为2 m温度的均方根误差(T2M_RMSE)、绝对误差(T2M_AE)和相对误差(T2M_RE)。

由图可得，对于24 h温度预报，采用倾向订正预报系统预报的温度无论是在相对误差、绝对误差和均方根误差等方面大部分时间都是优于原来模式预报的，只是在6~13 h预报，绝对误差和均方根误差略低于原来模式的预报，这段时间正是午后地面加热最强的时刻，对这段时间的订正系统设计可能还需要做适当的微细调整。同时也注意到，24 h温度预报的均方根误差和绝对误差在前6 h内误差出现了急剧的变化，而相对误差比较平稳，产生这种现象的原因是：温度绝对误差和均方根误差都是正值，即使预报的偏差放大；而相对误差是取的各站的区域平均值，它们既有正误差也有负误差，则取区域平均后，有可能使得正负误差抵消。本文中，在模式积分1 h时，由于温度订正后的结果与观测值相同，因此在模式积分1 h时，订正后的温度绝对误差和均方根误差都为零，从而使得订正前后的温度绝对误差和均方根误差相差明显，而相对误差由于正负抵消的原因，变化比较平稳。对于48 h温度预报，采用倾向订正预报系统预报的温度无论是在相对误差、绝对误差和均方根误差等方面基本上都是优于原来模式预报的。展现了很好的业务应用潜力。

5 结论

本文首先对数值模式预报产品的误差进行了分析，针对误差分析结果，首次提出了一种新的基于模式预报倾向的精细化预报方法，进行数值预报产品释用技术的研究和应用，并在此基础上设计开发了新疆精细化数值预报系统。初步数值试验结果表明，该方法对新疆地区的温度预报具有一定的正效果。后期经过调整订正系数，利用更多时次的观测资料进行温度订正，则有望可以使订正的温度更加接近观测。即该方法提高了新疆气象台站的气温预报准确率，展现了该方法的业务应用潜力。未来还需要做批量的数值试验，进一步检验和修正这种新的数值预报释用方法，不断使其完善，提高气象要素的预报准确率。