引言

随着计算机运算速度和人们对天气预报精细化程度需求的不断提高，高分辨率数值预报模式得到快速发展。提高模式分辨率的主要动机之一是改进和提高模式对中小尺度天气的预报能力，然而，增加模式的分辨率并不一定能提高预报准确率，高分辨率模式中的一些细小的相位误差可能导致模式低命中率和高的虚假预警率(Mass et al，2002), 加之一些中小尺度的物理过程并不完全清楚(Chakraborty，2008)，因此高分辨率数值模式的预报准确性还需要不断的检验。

通过检验了解模式的预报能力不仅可以为模式物理方案、参数化及陆面过程改进提供参考(陈海山等，2005；刘君等，2013；潘留杰等，2013)，而且可以为预报员使用模式提供更多有用的信息，增加预报员对模式的驾驭能力(贾丽红等，2012；陈超君等，2012；沈铁元等，2011；熊秋芬，2011)，从而做出更加准确的预报。已有的研究工作中，何立富等(2011)对国家强对流潜势预报业务进行了评估；Lean等(2008)检验了不同分辨率下英国气象局高分辨率数值预报模式的对流性降水预报能力；Gilleland等(2009)比较了5种方法对高分辨率模式降水预报的检验评分，认为观测网疏密程度对高分辨率模式的降水预报评分有重要影响。

ECMWF、日本数值预报模式产品在我国天气预报业务中有着广泛的应用(赵晓琳，2012)。但由于高分辨率模式应用时间比较短，使用上还存在一些盲目性。本文首先利用站点观测数据统计、对比模式预报能力的整体表现，在此基础上分析模式预报能力的地区性差异。

1 资料和方法 1.1 资料

使用的资料主要包括：(1)2012年4月1日至2013年3月31日全国2419个台站逐6 h降水量观测数据；(2) 每日08和20时(北京时，下同)发布的ECMWF高分辨率数值预报产品，空间分辨率0.25°×0.25°；(3) 每日02、08、14和20时发布的日本高分辨率数值预报产品，空间分辨率为0.5°×0.5°。受资料的限制，仅对比分析两个模式前84 h的降水预报能力；(4) CMORPH卫星与自动观测站的逐时降水量融合产品(http://www.escience.gov.cn/metdata/page/index.html[2013-03-31])，其空间分辨率0.1°×0.1°，检验不同区域降水预报能力的差异性时，分辨率插值成与模式格点一致的0.5°×0.5°。

1.2 方法

运用的方法包括：(1) 用标准差比率σ=σ_f/σ_o、相关系数R、均方根误差E来分析两个模式预报场与观测场的差异，并用泰勒图(Taylor，2001；张宏芳等，2011)表示。(2) 通过2×2列联表计算模式降水的4种评分指数(表 1)。

4种评分指数的公式分别为：(1) 预报偏差$ Bias = \frac{{A + B}}{{A + C}} $(Brier，1950)，表示预报事件发生的次数与观测事件发生的次数的比率；(2) 临界成功指数$ CSI = \frac{A}{{A + B + C}} $(Schaefer, 1990)，通常也称之为TS评分；(3) TSS评分(Peirce，1984)，$ TSS = \frac{{AD - BC}}{{\left({A + C} \right)(B + D)}} $，反映了成功预报与空报的差异，TSS=0表示无预报技巧；(4) HSS评分(Gilbert, 1984)，$ HSS = \frac{{A + D - E}}{{A + B + C + D - E}} $，其中$ E = \frac{{\left({A + C} \right)\left({A + B} \right) + \left({C + D} \right)\left({B + D} \right)}}{{A + B + C + D}} $，HSS表示除去随机事件发生后的预报准确率。

2 检验结果分析 2.1 相关性及误差

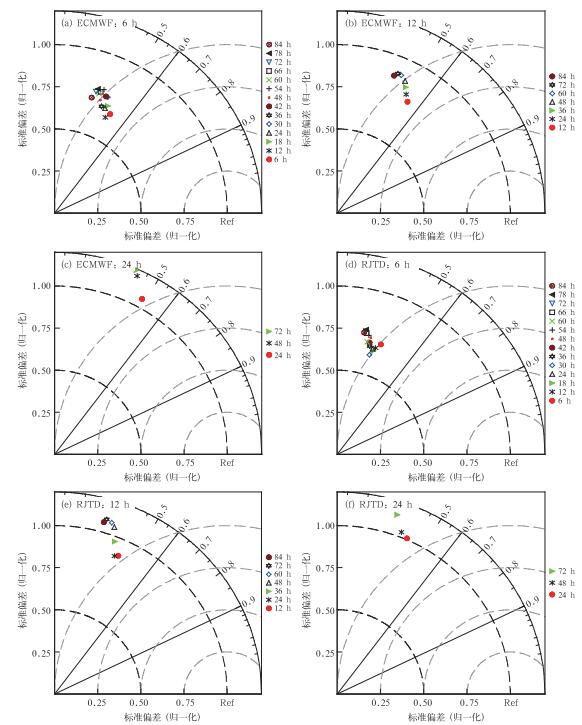
比较两家模式的相关系数可以发现，ECMWF显著优于日本模式，6 h分段ECMWF模式(图 1a)相关系数最大达0.48，最小为0.30，而日本模式(图 1d)0~6 h相关系数仅为0.36，最小为0.20，远远低于ECMWF模式，12和24 h分段降水与观测场的相关也有类似表现。随着分段间隔的增加，预报与观测的相关系数表现不单调，两个模式均在12 h分段降水上表现最好，24 h分段次之，6 h分段最差，即相关系数呈现出先上升后下降的趋势。

从预报与观测的标准差比值来看，ECMWF模式6 h(图 1a)、12 h(图 1b)分段预报σ < 1，表明模式预报降水的变化幅度较观测偏小，24 h(图 1c)分段则相反σ>1，表明模式的降水预报较观测振幅偏大。日本模式6和24 h分段降水量级预报与ECMWF模式基本类似，12 h分段降水较ECMWF模式量级预报更加合理。

比较两个模式标准差比值σ的变化情况可以发现，随着分段间隔的增加，标准差比值是逐渐增大的，而日本模式的调整更为迅速，12 h分段降水平均标准差比值接近于1左右，而ECMWF模式12 h平均标准差比值仅为0.73。两个模式均在0~24 h分段降水上σ最接近于1，模式预报与观测降水的振幅基本一致。此外，6 h分段中ECMWF模式σ无趋势性变化，而日本模式的30 h之前标准差比值σ是单调减小的，30 h之后逐渐增大，这可能反映了两个模式的不同参数化方案或物理机制。

在不同分段情况下，ECMWF模式均方根误差比率σ均小于日本模式，表明平均来说，ECMWF预报结果与观测更加一致。综合而言，日本模式比ECMWF模式降水预报离散度偏大，出现极端情况比率更大。ECMWF模式降水预报相对平稳，与观测值相关性较高，均方根误差较小，ECMWF高分辨模式对降水的预报优于日本模式。

2.2 技巧评分

考虑预报业务的实际需求，仅对逐6、12和24 h分段晴雨、暴雨预报评分进行检验，需要说明的是，按照降水等级划分标准，6、12和24 h降水量分别≥25、30和50 mm视为暴雨。另外，为了表述方便，文章中F表示模式预报值，O表示观测值。

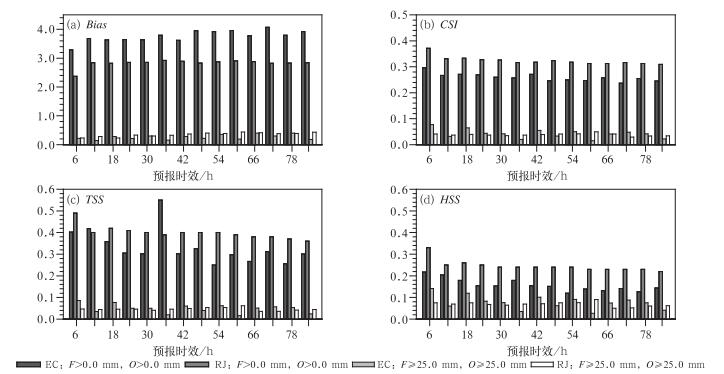
从预报偏差来看(图 2a)，晴雨预报中两个模式有雨预报频率较实际观测偏多，这一现象在ECMWF模式中表现更为显著。随着预报时效增加，ECMWF模式有雨预报频率逐渐增加，日本模式有雨预报频率在6 h有明显的跃变，6~84 h稳定维持或有下降的趋势。

分析两个模式对降水的预报差异发现，ECMWF、日本模式0~6 h预报(图 2b)成功率POD=A/(A+C)分别为0.96和0.94，到78~84 h下降为0.92和0.89，ECMWF模式预报成功率优于日本模式，但ECMWF模式空报率FAR=B/(A+B)平均高于日本模式0.13，导致ECMWF模式CSI评分偏低，这与预报偏差(Bias)反映的情况基本一致，在TSS评分(图 2c)上也表现出同样的结果，日本模式TSS评分整体高于ECMWF模式，除去随机事件后的晴雨预报评分指数HSS整体下降，但日本模式HSS评分仍然显著高于ECMWF模式。

两个模式的暴雨预报频率较实际偏低，ECMWF模式偏低更为明显，随着预报时效的增加，日本模式暴雨预报频率逐渐增加，ECMWF模式变化趋势不单调(图 2a)，整体而言，ECMWF模式暴雨CSI(图 2b)、TSS(图 2c)和HSS(图 2d)评分指数高于日本模式，但ECMWF模式表现不稳定，在一些时次，评分指数异常偏低，而日本模式相对稳定，距预报初始时刻越远，评分逐渐下降。

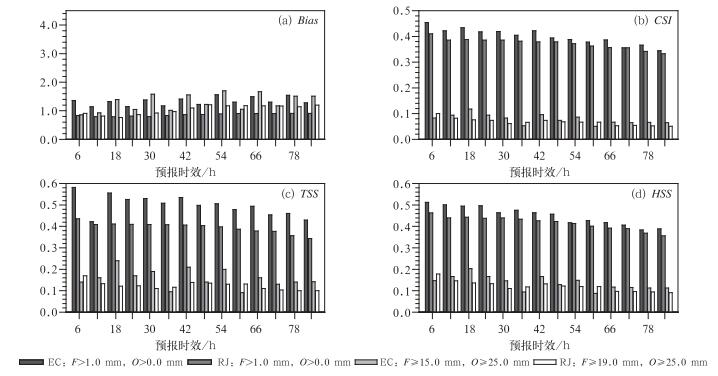
考虑到模式晴雨预报中降水发生的频率较实际偏高(Bias>1)，暴雨预报频率较实际偏少(Bias < 1)，减小晴雨预报中的降水频率，增加暴雨预报频率，可能会提高评分技巧，因此以日本模式为基础，调整降水事件频率，结果显示6 h分段晴雨预报阈值调整为F≥1.0 mm，O>0.0 mm；暴雨预报阈调整为：ECMWF模式F≥15.0 mm, O≥25.0 mm；日本模式F≥19.0 mm, O≥25.0 mm，Bias更接近于1。调整后，晴雨预报中降水频率偏多的情况得到显著改善(图 3a)，两个模式的CSI(图 3b)、TSS(图 3c)和HSS(图 3d)评分指数均大幅度提高，且ECMWF模式提高更为显著，优于日本模式。

调整暴雨预报阈值后，暴雨预报偏差Bias在1附近波动，与实际观测更加一致(图 3a)，ECMWF、日本模式CSI评分指数(图 3b)较调整前分别提高0.030和0.023，TSS(图 3c)、HSS(图 3d)评分显著提高，变化趋势和CSI基本一致，但ECMWF模式CSI、TSS、HSS评分随时间变化不稳定的情况并没有改善。需要说明的是调整阈值也在一定程度上增加了“空报”的风险。

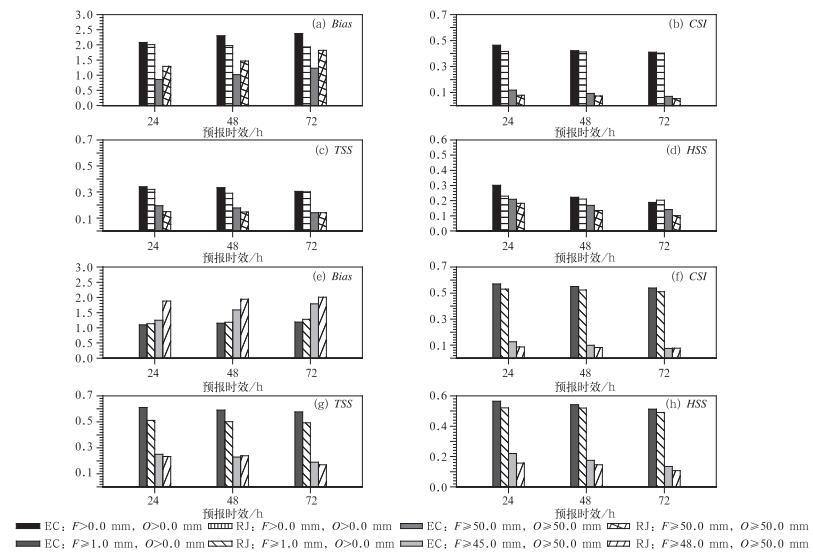
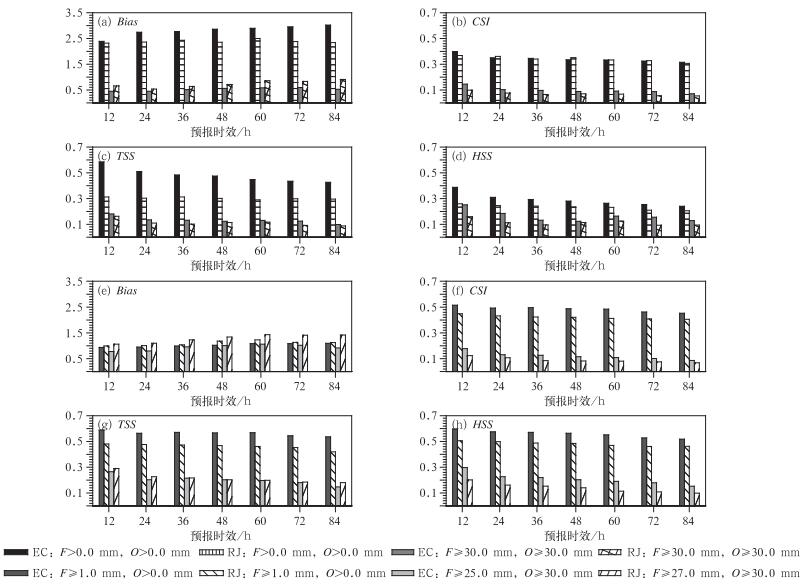
12 h分段晴雨预报降水频率偏多的情况较6 h分段有明显的改善(图 4a)，其中，ECMWF模式下降更为显著，从CSI评分(图 4b)来看，ECMWF模式48、60和72 h的TSS评分低于日本模式，其余时段均较日本模式高；无论是晴雨还是暴雨预报，ECMWF 12 h分段TSS评分(图 4c)整体高于日本模式；除去随机事件后，ECMWF模式HSS评分也整体优于日本模式。逐12 h分段暴雨预报频率较逐6 h明显增加(图 4a)，其中日本模式增加更为显著。就预报暴雨频率和观测的一致程度来看，日本模式更接近于实际情况，但日本模式暴雨预报CSI评分(图 4b)全部低于ECMWF模式，表明日本模式预报暴雨位置可能偏离实际位置较大，这与图 1b和1e中所表现的情况也基本一致；与晴雨预报不同，12 h分段ECMWF模式暴雨TSS(图 4c)、HSS评分(图 4d)一致高于日本模式或与之持平。

调整阈值，用F≥1.0 mm，O>0.0 mm来计算两个模式的晴雨预报评分；ECMWF模式：F≥25.0 mm, O≥30.0 mm，日本模式：F≥27.0 mm, O≥30.0 mm来计算暴雨预报评分。调整后，ECMWF模式晴雨预报降水发生频率较观测略偏多，日本模式12和24 h较观测偏低，36~84 h较观测发生频率偏高，平均为1.068，接近于理想情况。

调整后ECMWF模式暴雨预报频率0~12、12~24和72~84 h较观测偏低，其余时段较观测基本接近于1；日本模式12~24 h较观测频率偏低，其余时段一致偏高(图 4e)。调整阈值后，两个模式CSI评分(图 4f)均大幅度提高且ECMWF模式预报评分显著优于日本模式。与CSI评分类似，调整后TSS(图 4g)、HSS评分(图 4h)均大幅度提升，模式预报准确率增加，空报率减少，对偶然事件的预报能力提高(图 4h)。

24 h ECMWF、日本模式晴雨、暴雨预报偏差Bias(图 5a)较12 h进一步向理想值靠近，随着预报时效的增加单调上升。ECMWF模式晴雨预报中降水发生频率平均值为2.25，日本模式为2.09，仍然较观测降水发生频率偏高1倍以上；ECMWF模式暴雨预报频率均值接近于理想值，日本模式较实际偏高；ECMWF模式24 h晴雨、暴雨CSI评分(图 5b)优于日本模式，TSS评分(图 5c)则在24和48 h分段高于日本模式。分析发现，尽管ECMWF模式在48和72 h预报准确率较日本模式偏高，但空报率偏高更加显著；HSS评分(图 5d)表现与TSS类似。

采用阈值F≥1.0 mm，O>0.0 mm来计算模式24 h晴雨预报评分，结果发现，两个模式晴雨预报中降水发生的频率均接近于理想情况(图 5e)，评分技巧较调整前显著增加，且随着预报时效的增加，评分指数单调下降。

由于24 h ECMWF模式暴雨预报Bias接近于理想情况(图 5a)，日本模式Bias略高于1，采用调整暴雨预报频率的方法来提高预报技巧的空间不大，但略微增加暴雨预报频率在一定程度上仍然能够提高预报技巧。ECMWF采用阈值：F≥45.0 mm, O≥50.0 mm，日本模式：F≥48.0 mm, O≥50.0 mm来调整暴雨预报事件。结果暴雨预报频率较实际增多(图 5e)，就Bias和理想值接近的程度来看，为负效果，但CSI(图 5f)、TSS(图 5g)、HSS(图 5h)评分仍然较调整前略有提高。

2.3 空间分布

与站点统计结果相比，模式预报与CMORPH卫星降水融合资料有更好的一致性，模式晴雨预报中降水偏多的幅度有明显改善，从预报偏差来看，6 h (图 6a)降水预报偏多的情况主要出现在新疆南部、青海北部、甘肃、陕西、湖南部分及山西、山东、河南交界处，偏少情况主要出现在西藏、青海交界处及东北、我国南方沿海部分地区，大值中心位于新疆南部。

两家模式预报偏差地理分布总体是一致的，均表现为西北偏多，南方沿海地区预报偏少。随着分段长度的增加，两个模式预报偏多的情况明显增加，其中日本模式Bias增加更为明显，分布范围从西北向东南扩展，到24 h(图 6e)除海南、台湾、南部沿海及西南局部地区外，Bias均高于1，大值中心基本在新疆南部稳定维持。

从CSI评分来看，6 h分段(图 6b)大值中心出现在西藏南部、四川、云南、广西以及湖南、湖北、广西交界处，西北地区的新疆、内蒙古、甘肃、西藏、青海等部分地区CSI小于0.35。随着分段间隔的增加，ECMWF模式CSI快速增加，12和24 h分段，ECMWF模式CSI显著优于日本模式，大值中心出现在我国西南地区，24 h部分地区CSI达0.6或以上。总体而言，模式在东南地区预报技巧优于西北地区。

3 结论

利用泰勒图、技巧评分等方法，客观对比分析ECMWF、日本高分辨率模式对中国降水的预报能力，结论如下：

(1) ECMWF模式预报降水与观测的相关性显著高于日本模式。随着分段间隔的增加，模式预报与观测的相关系数变化不单调，两个模式均在12 h分段降水上表现最好，24 h分段次之，6 h分段最差。

(2) ECMWF模式6和12 h分段预报标准差比率σ < 1，预报降水的变化幅度较观测偏小，24 h分段则相反σ>1，表明模式预报的降水较观测振幅偏大；日本模式6和24 h分段降水量级预报与ECMWF模式基本类似，12 h分段降水较ECMWF模式量级预报更加合理。从均方根误差来看，ECMWF模式均方根误差小于日本模式，整体来说ECMWF模式降水预报与观测更加一致。

(3) 两个模式晴雨预报中降水发生频率较实际偏高，暴雨预报频率较实际偏低，随着分段间隔的增加，这一情况有所改善，晴雨预报中降水发生频率24 h分段表现最好，6 h分段表现最差；暴雨发生频率，ECMWF、日本模式分别在24和12 h表现最好。整体来说，ECMWF模式6 h分段降水晴雨预报评分低于日本模式，暴雨预报评分整体高于日本模式；12和24 h分段ECMWF模式晴雨、暴雨预报评分一致高于日本模式，TSS、HSS表现与CSI类似。

(4) 调整模式降水预报频次可以在一定程度上提高技巧评分；与站点统计结果相比，模式预报与CMORPH卫星降水融合资料有更好的一致性，模式晴雨预报中降水偏多的幅度有明显改善，总体而言，ECMWF模式优于日本模式，东南地区技巧评分Bias、CSI优于西北地区。